苏科版七年级数学下册 第9章 数学活动 拼图·公式 课件(共23张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 第9章 数学活动 拼图·公式 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 299.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 16:34:52 | ||
图片预览

文档简介
(共23张PPT)
数学活动 拼图·公式
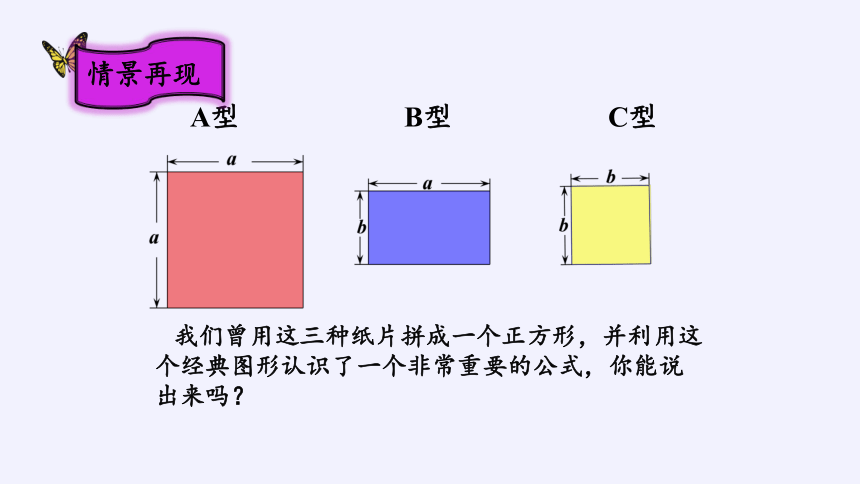
A型 B型 C型
我们曾用这三种纸片拼成一个正方形,并利用这个经典图形认识了一个非常重要的公式,你能说出来吗?
情景再现
数
形
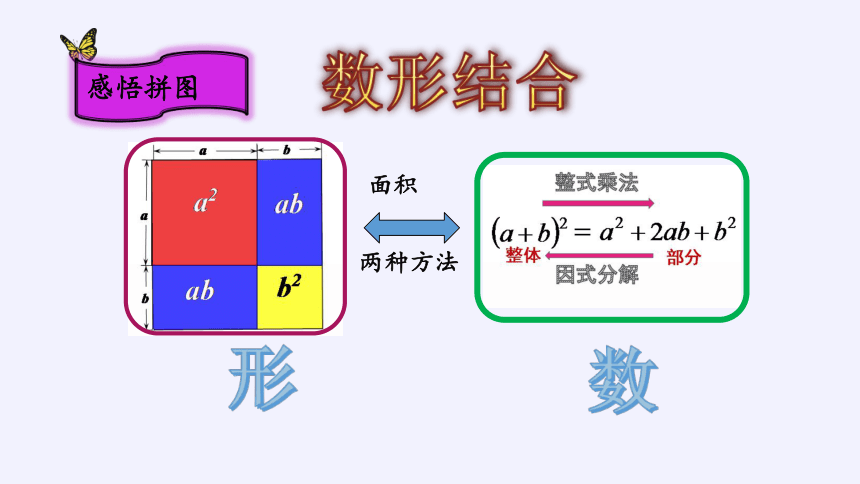
面积
两种方法
数形结合
感悟拼图
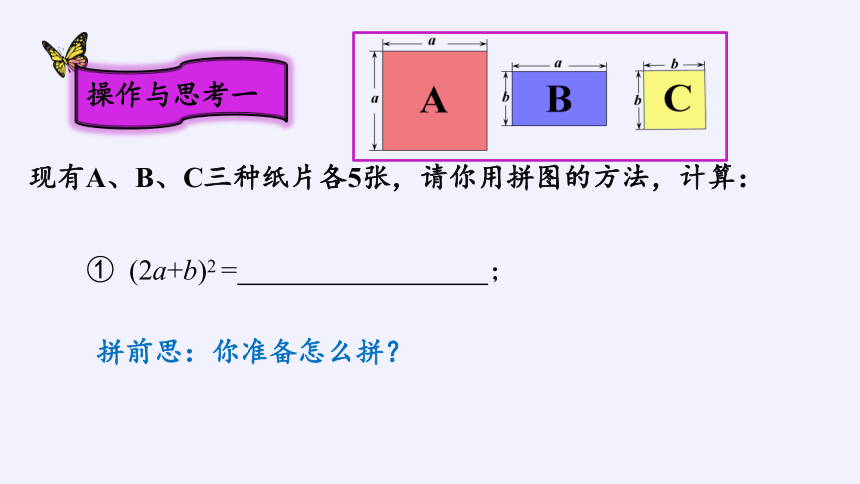
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
拼前思:你准备怎么拼?
① (2a+b)2 = ;
操作与思考一
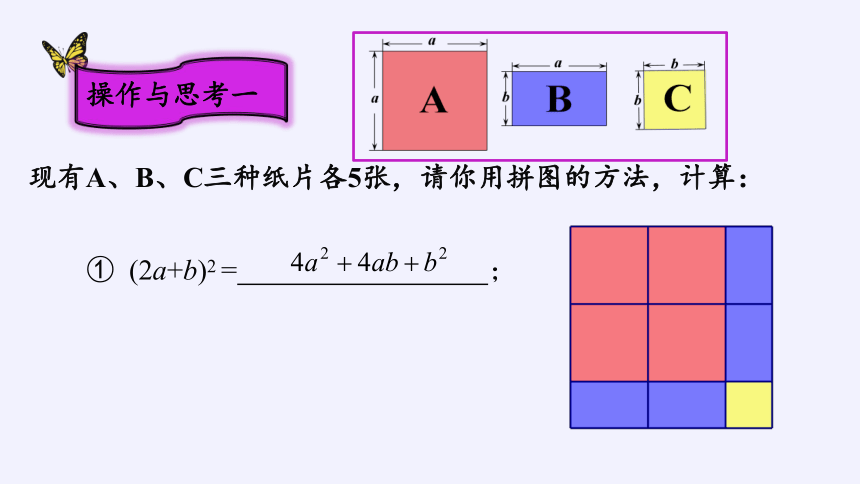
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
① (2a+b)2 = ;
操作与思考一
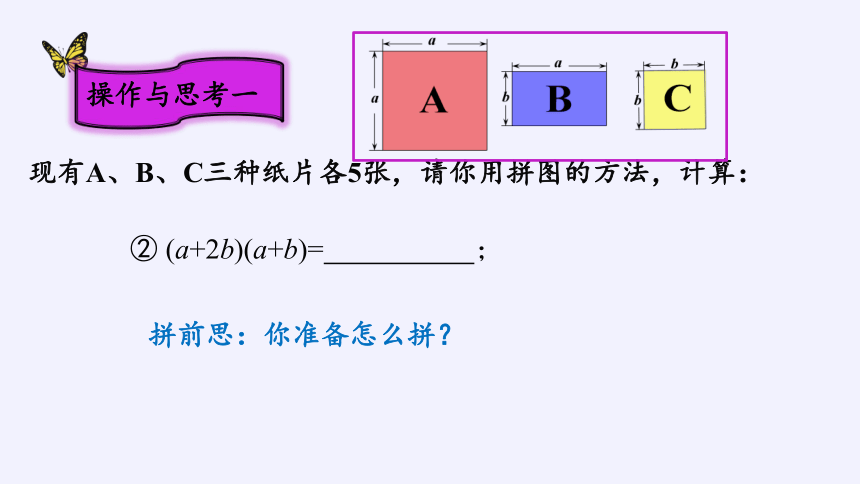
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
拼前思:你准备怎么拼?
② (a+2b)(a+b)= ;
操作与思考一
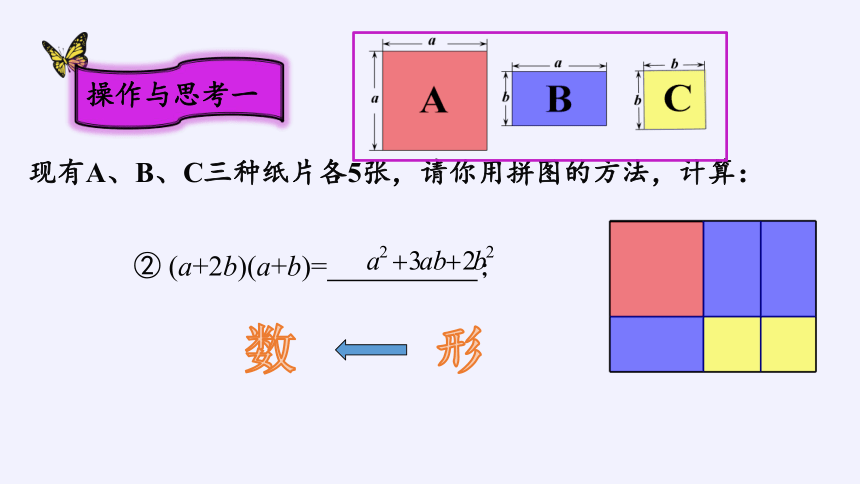
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
② (a+2b)(a+b)= ;
操作与思考一
形
数
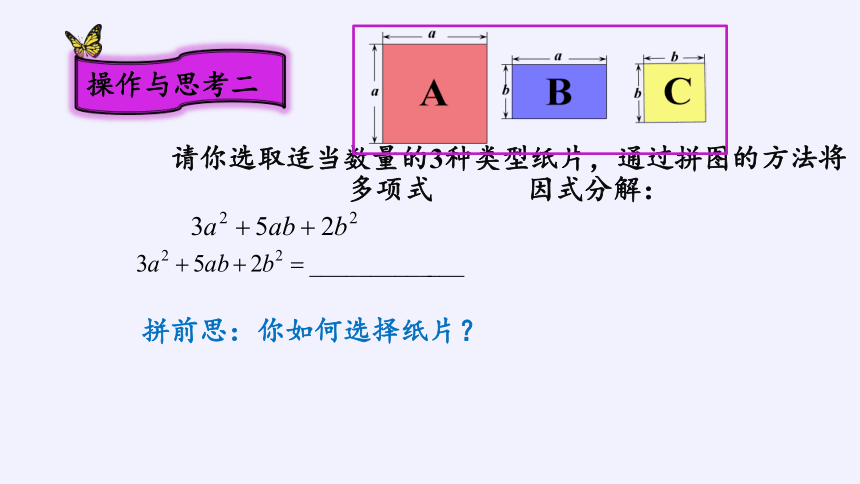
请你选取适当数量的3种类型纸片,通过拼图的方法将多项式 因式分解:
操作与思考二
拼前思:你如何选择纸片?
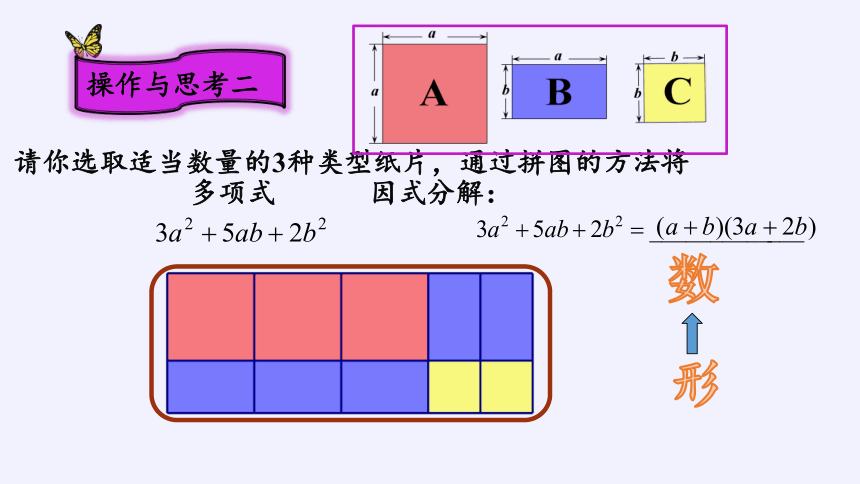
请你选取适当数量的3种类型纸片,通过拼图的方法将多项式 因式分解:
操作与思考二
形
数
拼图的一般方法
2. 先正后矩
3.先大后小
4.大小对角
1.等边相连
归纳
不能,因为多项式a2+4ab+b2不能因式分解
你能拼成一个面积为 的长方形吗?
操作与思考三
能因式分解的二次多项式才能表示一个长方形的面积.
如何只添加(或减少)一种纸片数量,使之拼成一个长方形?
议一议
4人小组讨论
原面积
变化类型 张数 面积变化 因式分解
增加A型 3张 +3a2 4a2+4ab+b2=(2a+b)2
增加A型 2张 +2a2 3a2+4ab+b2=(a+b)(3a+b)
减少A型 1张 -a2 4ab+b2=b(4a+b)
减少B型 2张 -2ab a2+2ab+b2=(a+b)2
增加C型 3张 +3b2 a2+4ab+4b2=(a+2b)2
增加C型 2张 +2b2 a2+4ab+3b2=(a+b)(a+3b)
减少C型 1张 -b2 a2+4ab=a(a+4b)
数
形
共能拼出7种长方形
分类讨论
三种纸片各有10张,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(所拼的图中既不能有缝隙,也不能有重合部分),能拼成几种不同的正方形,写出拼成的正方形的边长,并说说你的思路.
延伸与拓展
4人小组讨论
边长 总面积 各项系数
a+b (a+b)2=a2+2ab+b2 1,2,1
a+2b (a+2b)2=a2+4ab+4b2 1,4,4
a+3b (a+3b)2=a2+6ab+9b2 1,6,9
2a+b (2a+b)2=4a2+4ab+b2 4,4,1
2a+2b (2a+2b)2=4a2+8ab+4b2 4,8,4
3a+b (3a+b)2=9a2+6ab+b2 9,6,1
数
形
有条理的思考
能拼出6种
不同的正方形
三种纸片各有20张,从其中取出17张纸片,每种纸片至少取出一张,取出的这些纸片能否拼成一个正方形(所拼的图中既不能有缝隙,也不能有重合部分),说说你的理由.
延伸与拓展
拼前思:这里的17是指的什么?
交流
序号 正方形边长 总面积 各项系数 各项系数的和
1 a+b (a+b)2=a2+2ab+b2 1,2,1 4
2 a+2b (a+2b)2=a2+4ab+4b2 1,4,4 9
3 a+3b (a+3b)2=a2+6ab+9b2 1,6,9 16
4 2a+b (2a+b)2=4a2+4ab+b2 4,4,1 9
5 2a+2b (2a+2b)2=4a2+8ab+4b2 4,8,4 16
6 3a+b (3a+b)2=9a2+6ab+b2 9,6,1 16
完
全
平
方
数
17不是完全平方数,所以拼不出来.
不完全归纳
你能证明你的结论吗?
交流
序号 正方形边长 总面积 各项系数 各项系数的和
1 a+b (a+b)2=a2+2ab+b2 1,2,1 4
2 a+2b (a+2b)2=a2+4ab+4b2 1,4,4 9
... ... ... ... ...
k ma+nb (ma+nb)2=m2a2+2mnab+n2b2 m2,2mn,n2 m2+2mn+n2
因为m2+2mn+n2 =(m+n)2
所以能拼成正方形的纸片的总数量一定是完全平方数
更加理性地思考问题
通过本课的学习,你有哪些收获?
课堂小结
知识回顾
1.拼图的方法:
等边相连,先正后矩,先大后小,大小对角;
2.数形结合:两种方法对同一图形求面积
3.分类讨论:有条理地思考
课后,你还准备对哪些方面进行进一步的研究?
课堂小结
数缺形时少直观,
形少数时难入微。
数形结合百般好,
隔离分家万事休。
——华罗庚
数
形
结
合
谢 谢
数学活动 拼图·公式
A型 B型 C型
我们曾用这三种纸片拼成一个正方形,并利用这个经典图形认识了一个非常重要的公式,你能说出来吗?
情景再现
数
形
面积
两种方法
数形结合
感悟拼图
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
拼前思:你准备怎么拼?
① (2a+b)2 = ;
操作与思考一
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
① (2a+b)2 = ;
操作与思考一
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
拼前思:你准备怎么拼?
② (a+2b)(a+b)= ;
操作与思考一
现有A、B、C三种纸片各5张,请你用拼图的方法,计算:
② (a+2b)(a+b)= ;
操作与思考一
形
数
请你选取适当数量的3种类型纸片,通过拼图的方法将多项式 因式分解:
操作与思考二
拼前思:你如何选择纸片?
请你选取适当数量的3种类型纸片,通过拼图的方法将多项式 因式分解:
操作与思考二
形
数
拼图的一般方法
2. 先正后矩
3.先大后小
4.大小对角
1.等边相连
归纳
不能,因为多项式a2+4ab+b2不能因式分解
你能拼成一个面积为 的长方形吗?
操作与思考三
能因式分解的二次多项式才能表示一个长方形的面积.
如何只添加(或减少)一种纸片数量,使之拼成一个长方形?
议一议
4人小组讨论
原面积
变化类型 张数 面积变化 因式分解
增加A型 3张 +3a2 4a2+4ab+b2=(2a+b)2
增加A型 2张 +2a2 3a2+4ab+b2=(a+b)(3a+b)
减少A型 1张 -a2 4ab+b2=b(4a+b)
减少B型 2张 -2ab a2+2ab+b2=(a+b)2
增加C型 3张 +3b2 a2+4ab+4b2=(a+2b)2
增加C型 2张 +2b2 a2+4ab+3b2=(a+b)(a+3b)
减少C型 1张 -b2 a2+4ab=a(a+4b)
数
形
共能拼出7种长方形
分类讨论
三种纸片各有10张,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(所拼的图中既不能有缝隙,也不能有重合部分),能拼成几种不同的正方形,写出拼成的正方形的边长,并说说你的思路.
延伸与拓展
4人小组讨论
边长 总面积 各项系数
a+b (a+b)2=a2+2ab+b2 1,2,1
a+2b (a+2b)2=a2+4ab+4b2 1,4,4
a+3b (a+3b)2=a2+6ab+9b2 1,6,9
2a+b (2a+b)2=4a2+4ab+b2 4,4,1
2a+2b (2a+2b)2=4a2+8ab+4b2 4,8,4
3a+b (3a+b)2=9a2+6ab+b2 9,6,1
数
形
有条理的思考
能拼出6种
不同的正方形
三种纸片各有20张,从其中取出17张纸片,每种纸片至少取出一张,取出的这些纸片能否拼成一个正方形(所拼的图中既不能有缝隙,也不能有重合部分),说说你的理由.
延伸与拓展
拼前思:这里的17是指的什么?
交流
序号 正方形边长 总面积 各项系数 各项系数的和
1 a+b (a+b)2=a2+2ab+b2 1,2,1 4
2 a+2b (a+2b)2=a2+4ab+4b2 1,4,4 9
3 a+3b (a+3b)2=a2+6ab+9b2 1,6,9 16
4 2a+b (2a+b)2=4a2+4ab+b2 4,4,1 9
5 2a+2b (2a+2b)2=4a2+8ab+4b2 4,8,4 16
6 3a+b (3a+b)2=9a2+6ab+b2 9,6,1 16
完
全
平
方
数
17不是完全平方数,所以拼不出来.
不完全归纳
你能证明你的结论吗?
交流
序号 正方形边长 总面积 各项系数 各项系数的和
1 a+b (a+b)2=a2+2ab+b2 1,2,1 4
2 a+2b (a+2b)2=a2+4ab+4b2 1,4,4 9
... ... ... ... ...
k ma+nb (ma+nb)2=m2a2+2mnab+n2b2 m2,2mn,n2 m2+2mn+n2
因为m2+2mn+n2 =(m+n)2
所以能拼成正方形的纸片的总数量一定是完全平方数
更加理性地思考问题
通过本课的学习,你有哪些收获?
课堂小结
知识回顾
1.拼图的方法:
等边相连,先正后矩,先大后小,大小对角;
2.数形结合:两种方法对同一图形求面积
3.分类讨论:有条理地思考
课后,你还准备对哪些方面进行进一步的研究?
课堂小结
数缺形时少直观,
形少数时难入微。
数形结合百般好,
隔离分家万事休。
——华罗庚
数
形
结
合
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
