苏科版七年级数学下册 7.5 多边形的内角和与外角和 课件(共20张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.5 多边形的内角和与外角和 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 537.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
7.5 多边形的内角和与外角和
美国国防部大楼——五角大楼
教学环节(一)智慧启迪:
激趣导入 目标定向
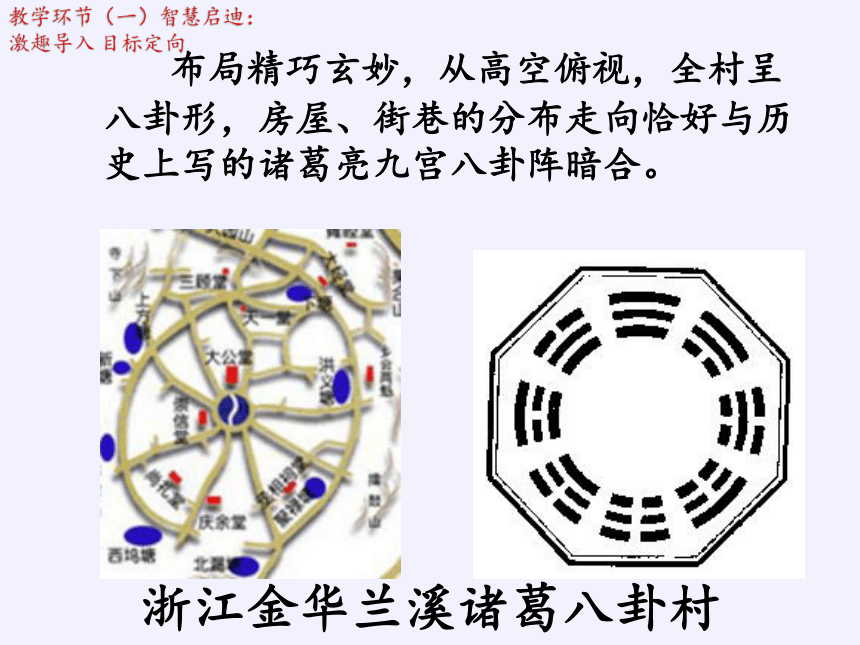
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
浙江金华兰溪诸葛八卦村
教学环节(一)智慧启迪:
激趣导入 目标定向
人教版数学教材八年级上
11.3.1多边形
自学19-20页回答一下问题:
1.什么叫多边形?为什么要说在平面内?
2.什么叫多边形的顶点?边?内角?外角?请画一个五边形分别说明。
3.什么叫多边形的对角线?一个五边形从一个顶点出发能作几条对角线?
4. 正多边形必须满足几个条件?长方形是正多边形吗?为什么?
教学环节(二)智慧萌芽:
多元引领 自主学面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
多边形的定义及分类
分类的标准:按组成多边形的线段的条数来分:
由n条线段组成的多边形称为n边形
(n≥3的整数)
多边形可以分为三角形、四边形、五边形、……
n边形
教学环节(二)智慧萌芽:
多元引领 自主学习
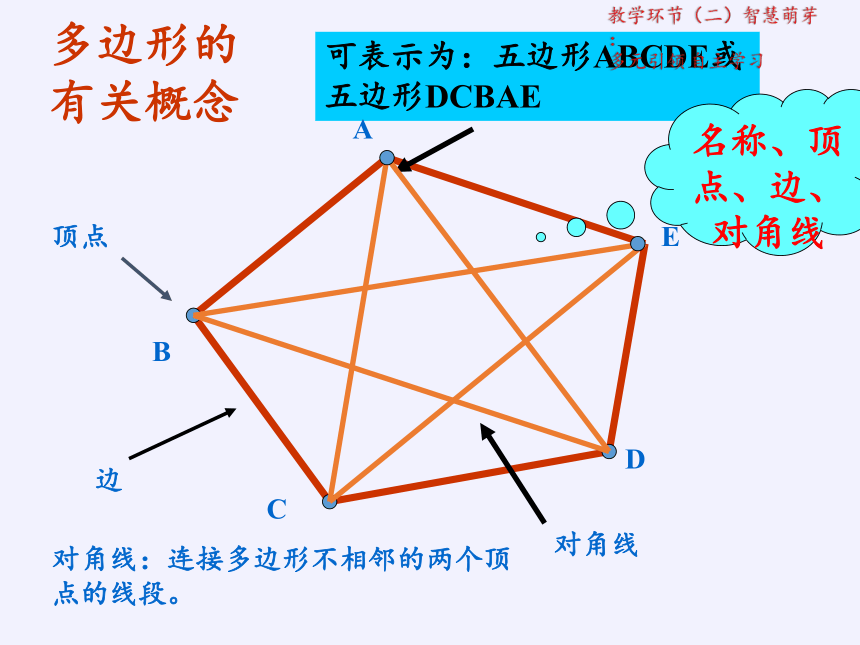
多边形的有关概念
顶点
边
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
名称、顶点、边、对角线
教学环节(二)智慧萌芽:
多元引领 自主学习
A
B
C
D
1
2
3
4
5
E
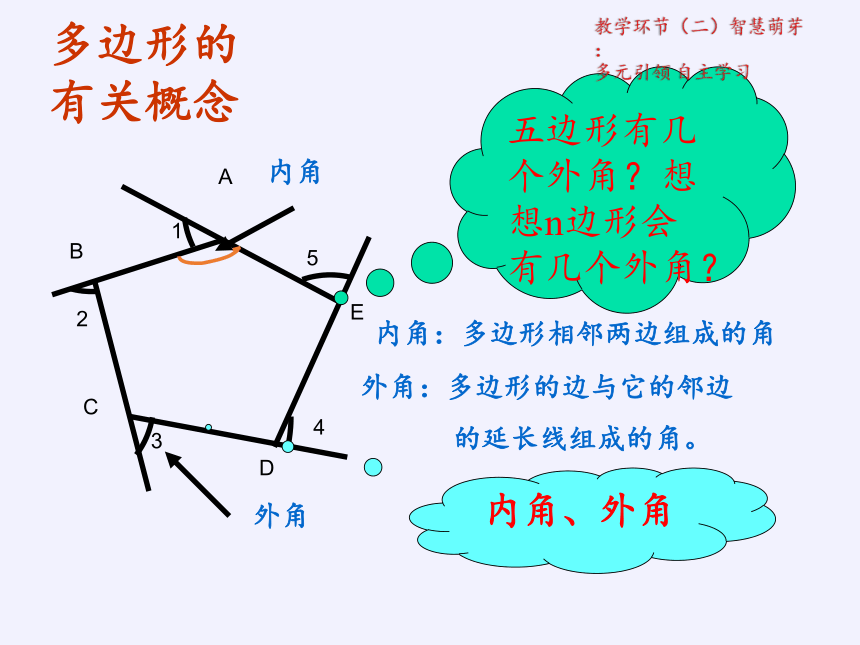
内角:多边形相邻两边组成的角
外角:多边形的边与它的邻边
的延长线组成的角。
内角
外角
五边形有几个外角?想想n边形会有几个外角?
多边形的有关概念
内角、外角
教学环节(二)智慧萌芽:
多元引领 自主学习
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数 …
总的对角线条数 …
0
0
1
2
2
5
3
9
4
14
n-3
n(n-3)
2
探究1
请大家细心地填一填,你能发现什么规律?
教学环节(三)智慧共生:
合作探究 个性展示
重要结论
2.从n边形的n个顶点出发共可以引多少条对角线?
A2
A3
A4
A5
An
A1
1.从n边形的一个顶点出发,可以
引 条对角线.
n-3
n(n-3)
2
An-3
A1
教学环节(三)智慧共生:
合作探究 个性展示
请你根据上图完成下面的这个表格:
(n-2)×180 °
900°
720 °
540°
360 °
n-2
5
4
3
2
…
180°
…
1
多边形的内角和
分成的三角形的个数
n
…
7
6
5
4
3
多边形的边数
(n-2)×180 °
n边形的内角和为
n边形从一个顶点出发可以将多边形分成多少个三角形?你能由此推出多边形的内角和吗?
n表示什么
n≥3且n为正整数
探究2
教学环节(三)智慧共生:
合作探究 个性展示
口答:五边形、六边形、七边形的内角和分别是多少?
下面左图所示的图形也是多边形,但不在我们现在研究的范围内 。
注 意
没有特别说明,我们研究的多边形都是指凸多边形.
有什么不同?
凹多边形
凸多边形
多边形的分类
教学环节(三)智慧共生:
合作探究 个性展示
(1)一个多边形的边都相等,它的内角一定都相等吗?为什么?
(2)一个多边形的内角都相等,它的边一定都相等吗?为什么
等边三角形
正方形
菱形
矩形
探究3
教学环节(三)智慧共生:
合作探究 个性展示
小结
1.多边形的几个概念整理
2.正多边形条件
教学环节(四)智慧发展:
点拨释疑 总结思变
3.思想和方法整理
1.下列不是凸多边形的是( )
A B C D
C
教学环节(五)智慧生成(创造):
反馈训练 综合创新
巩固练习:
2.下列叙述正确的是( )
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线, 这个多边形都在这条直线的同一侧,那么
它一定是凹多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
D
3.小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
D
巩固练习:
教学环节(五)智慧生成(创造):
反馈训练 综合创新
4.十二边形的内角和________
5.从十边形的一个顶点出发引对角线,把十边形分成______三角形,十边形共有 条对角线
1800°
八
35
谢 谢
7.5 多边形的内角和与外角和
美国国防部大楼——五角大楼
教学环节(一)智慧启迪:
激趣导入 目标定向
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
浙江金华兰溪诸葛八卦村
教学环节(一)智慧启迪:
激趣导入 目标定向
人教版数学教材八年级上
11.3.1多边形
自学19-20页回答一下问题:
1.什么叫多边形?为什么要说在平面内?
2.什么叫多边形的顶点?边?内角?外角?请画一个五边形分别说明。
3.什么叫多边形的对角线?一个五边形从一个顶点出发能作几条对角线?
4. 正多边形必须满足几个条件?长方形是正多边形吗?为什么?
教学环节(二)智慧萌芽:
多元引领 自主学面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
多边形的定义及分类
分类的标准:按组成多边形的线段的条数来分:
由n条线段组成的多边形称为n边形
(n≥3的整数)
多边形可以分为三角形、四边形、五边形、……
n边形
教学环节(二)智慧萌芽:
多元引领 自主学习
多边形的有关概念
顶点
边
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
名称、顶点、边、对角线
教学环节(二)智慧萌芽:
多元引领 自主学习
A
B
C
D
1
2
3
4
5
E
内角:多边形相邻两边组成的角
外角:多边形的边与它的邻边
的延长线组成的角。
内角
外角
五边形有几个外角?想想n边形会有几个外角?
多边形的有关概念
内角、外角
教学环节(二)智慧萌芽:
多元引领 自主学习
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数 …
总的对角线条数 …
0
0
1
2
2
5
3
9
4
14
n-3
n(n-3)
2
探究1
请大家细心地填一填,你能发现什么规律?
教学环节(三)智慧共生:
合作探究 个性展示
重要结论
2.从n边形的n个顶点出发共可以引多少条对角线?
A2
A3
A4
A5
An
A1
1.从n边形的一个顶点出发,可以
引 条对角线.
n-3
n(n-3)
2
An-3
A1
教学环节(三)智慧共生:
合作探究 个性展示
请你根据上图完成下面的这个表格:
(n-2)×180 °
900°
720 °
540°
360 °
n-2
5
4
3
2
…
180°
…
1
多边形的内角和
分成的三角形的个数
n
…
7
6
5
4
3
多边形的边数
(n-2)×180 °
n边形的内角和为
n边形从一个顶点出发可以将多边形分成多少个三角形?你能由此推出多边形的内角和吗?
n表示什么
n≥3且n为正整数
探究2
教学环节(三)智慧共生:
合作探究 个性展示
口答:五边形、六边形、七边形的内角和分别是多少?
下面左图所示的图形也是多边形,但不在我们现在研究的范围内 。
注 意
没有特别说明,我们研究的多边形都是指凸多边形.
有什么不同?
凹多边形
凸多边形
多边形的分类
教学环节(三)智慧共生:
合作探究 个性展示
(1)一个多边形的边都相等,它的内角一定都相等吗?为什么?
(2)一个多边形的内角都相等,它的边一定都相等吗?为什么
等边三角形
正方形
菱形
矩形
探究3
教学环节(三)智慧共生:
合作探究 个性展示
小结
1.多边形的几个概念整理
2.正多边形条件
教学环节(四)智慧发展:
点拨释疑 总结思变
3.思想和方法整理
1.下列不是凸多边形的是( )
A B C D
C
教学环节(五)智慧生成(创造):
反馈训练 综合创新
巩固练习:
2.下列叙述正确的是( )
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线, 这个多边形都在这条直线的同一侧,那么
它一定是凹多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
D
3.小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
D
巩固练习:
教学环节(五)智慧生成(创造):
反馈训练 综合创新
4.十二边形的内角和________
5.从十边形的一个顶点出发引对角线,把十边形分成______三角形,十边形共有 条对角线
1800°
八
35
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
