华东师大版八年级下册数学 18.2 平行四边形的判定 课件(共20张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 18.2 平行四边形的判定 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 327.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 14:50:05 | ||
图片预览







文档简介
(共20张PPT)
18.2 平行四边形的判定
我们学习了哪些判定平行四边形的方法?
1、平行四边形的定义;
2、两组对边分别相等的四边形是平行四边形;
3、一组对边平行且相等的四边形是平行四边形 。
1.知识:理解并掌握平行四边形的判定方法(判定定理三);
2.能力:能运用这种方法来证明一个四边形是平行四边形.
3. 习题:完成教材P87练习,《学习检测》P58-61练习。
自学指导
1、自学教材P85-87,初步完成教材例题,课后练习以及《学习检测》P58-61。
2、教材至少读练两遍,适当加快速度。
3、前十分钟独立思考与学习,不要出声,十
分钟后可以在不影响别人的情况下讨论。
4、合理使用练习本。
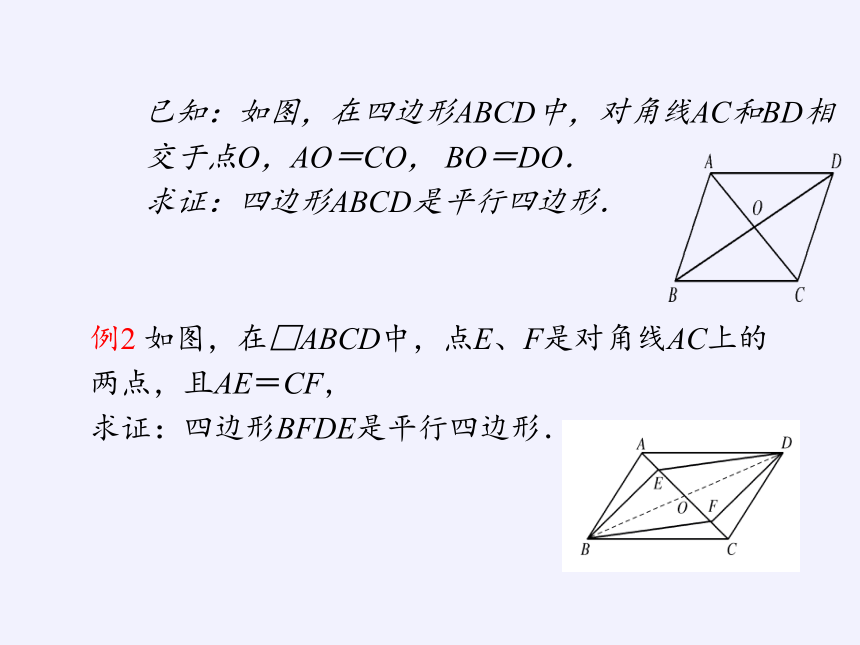
已知:如图,在四边形ABCD中,对角线AC和BD相交于点O,AO=CO, BO=DO.
求证:四边形ABCD是平行四边形.
例2 如图,在□ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
平行四边形的对角线具有什么性质?
这个命题的逆命题是什么?
平行四边形的对角线互相平分。
对角线互相平分的四边形是平行四边形.
它是真命题吗?
已知:如图,在四边形ABCD中,对角线AC和BD相交于点O,AO=CO, BO=DO.
求证:四边形ABCD是平行四边形.
分析:要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
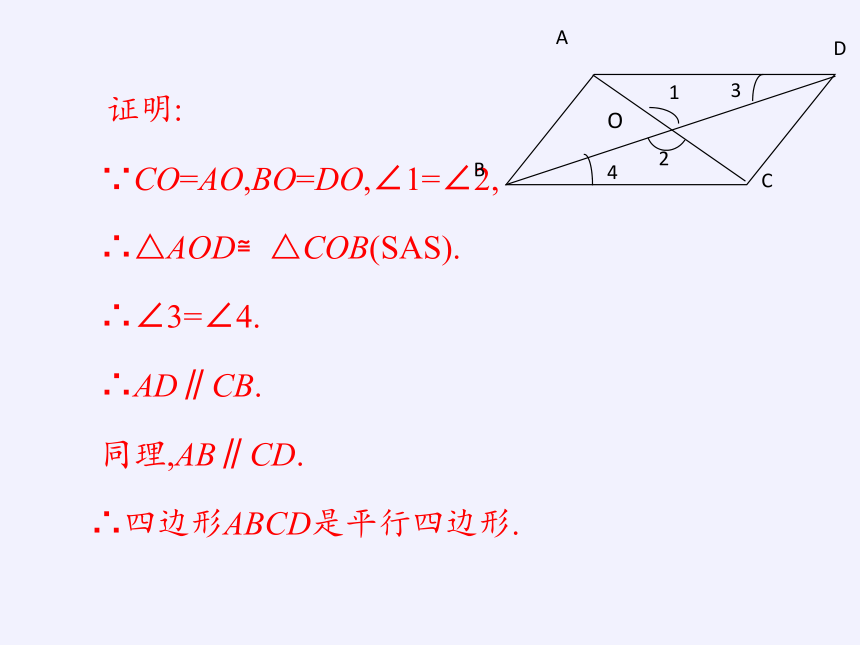
证明:
∵CO=AO,BO=DO,∠1=∠2,
∴△AOD≌△COB(SAS).
∴∠3=∠4.
∴AD∥CB.
同理,AB∥CD.
∴四边形ABCD是平行四边形.
B
D
C
A
O
4
3
2
1
例2 如图,在□ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
分析:连结BD,交AC于点O,由于OB=OD ,因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当,根据题意只需证明OE=OF.
证明: 连结BD,交AC于点O
∵ 四边形ABCD是平行四边形
∴ OB=OD, OA=OC。
∵ AE=FC,
∴ OE=OF,
∴ 四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得□ABCD;
⑵若AB=CD,______,则得□ ABCD;
⑶若AC=8,BD=10,AO=4,_______,则得□ ABCD
A
D
B
C
O
1、补充一个合适的条件使⑴—⑶小题成立:
C
A
D
B
E
G
H
F
O
2、□ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH___平行四边形.(填“是”或“不是”)
3.如图,在平行四边形ABCD中,已知两条对角线相交于点O, E、F、G、H分别是AO、BO、CO、DO的中点,以图中的点为顶点,尽可能多地画出平行四边形.
(1)连结EF、FG、GH、HE
(2)连结EB、BG、GD、DE
(3)连结AF、FC、CH、HA
创新训练:
(1)一组对边平行,一组对边相等的四边形是平行四边形吗?
(2)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?
1.延长△ABC的中线AD至E,使得DE=AD,那么四边形ABEC是平行四边形吗? 请写出证明过程?
E
当堂达标
思考:
现在我们总共学会了多少种判定平行四边形的方法了?
这些判定方法与平行四边形的性质之间,又有什么样的关系呢?
3、一组对边平行且相等的四边形是平行四边形
边
对角线
1、平行四边形的定义:两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形。
P87 练习 第2、3题
作业
谢 谢
18.2 平行四边形的判定
我们学习了哪些判定平行四边形的方法?
1、平行四边形的定义;
2、两组对边分别相等的四边形是平行四边形;
3、一组对边平行且相等的四边形是平行四边形 。
1.知识:理解并掌握平行四边形的判定方法(判定定理三);
2.能力:能运用这种方法来证明一个四边形是平行四边形.
3. 习题:完成教材P87练习,《学习检测》P58-61练习。
自学指导
1、自学教材P85-87,初步完成教材例题,课后练习以及《学习检测》P58-61。
2、教材至少读练两遍,适当加快速度。
3、前十分钟独立思考与学习,不要出声,十
分钟后可以在不影响别人的情况下讨论。
4、合理使用练习本。
已知:如图,在四边形ABCD中,对角线AC和BD相交于点O,AO=CO, BO=DO.
求证:四边形ABCD是平行四边形.
例2 如图,在□ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
平行四边形的对角线具有什么性质?
这个命题的逆命题是什么?
平行四边形的对角线互相平分。
对角线互相平分的四边形是平行四边形.
它是真命题吗?
已知:如图,在四边形ABCD中,对角线AC和BD相交于点O,AO=CO, BO=DO.
求证:四边形ABCD是平行四边形.
分析:要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
证明:
∵CO=AO,BO=DO,∠1=∠2,
∴△AOD≌△COB(SAS).
∴∠3=∠4.
∴AD∥CB.
同理,AB∥CD.
∴四边形ABCD是平行四边形.
B
D
C
A
O
4
3
2
1
例2 如图,在□ABCD中,点E、F是对角线AC上的两点,且AE=CF,
求证:四边形BFDE是平行四边形.
分析:连结BD,交AC于点O,由于OB=OD ,因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当,根据题意只需证明OE=OF.
证明: 连结BD,交AC于点O
∵ 四边形ABCD是平行四边形
∴ OB=OD, OA=OC。
∵ AE=FC,
∴ OE=OF,
∴ 四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得□ABCD;
⑵若AB=CD,______,则得□ ABCD;
⑶若AC=8,BD=10,AO=4,_______,则得□ ABCD
A
D
B
C
O
1、补充一个合适的条件使⑴—⑶小题成立:
C
A
D
B
E
G
H
F
O
2、□ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH___平行四边形.(填“是”或“不是”)
3.如图,在平行四边形ABCD中,已知两条对角线相交于点O, E、F、G、H分别是AO、BO、CO、DO的中点,以图中的点为顶点,尽可能多地画出平行四边形.
(1)连结EF、FG、GH、HE
(2)连结EB、BG、GD、DE
(3)连结AF、FC、CH、HA
创新训练:
(1)一组对边平行,一组对边相等的四边形是平行四边形吗?
(2)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?
1.延长△ABC的中线AD至E,使得DE=AD,那么四边形ABEC是平行四边形吗? 请写出证明过程?
E
当堂达标
思考:
现在我们总共学会了多少种判定平行四边形的方法了?
这些判定方法与平行四边形的性质之间,又有什么样的关系呢?
3、一组对边平行且相等的四边形是平行四边形
边
对角线
1、平行四边形的定义:两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
4、对角线互相平分的四边形是平行四边形。
P87 练习 第2、3题
作业
谢 谢
