苏科版七年级数学下册 7.2 探索平行线的性质 课件(共29张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.2 探索平行线的性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 16:58:20 | ||
图片预览





文档简介
(共29张PPT)
7.2 探索平行线的性质
学习目标
1、掌握平行线的判定和性质,
以及它们的区别;
2、能熟练、准确、灵活地应用
平行线的判定和性质解决问题。
知识梳理
一、平行线的性质
1、两直线平行,同位角相等
2、两直线平行,内错角相等
3、两直线平行,同旁内角互补
二、平行线的判定
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
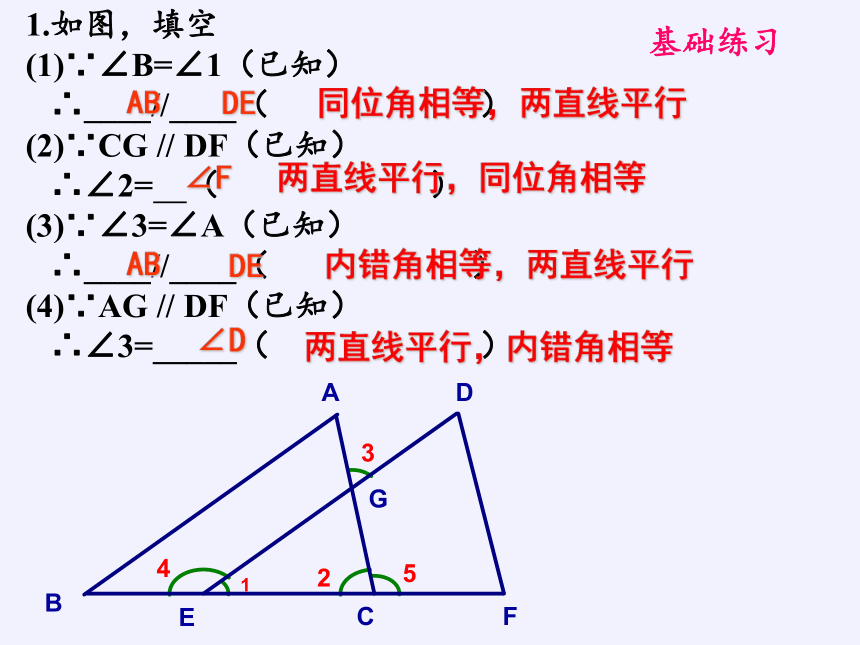
1.如图,填空
(1)∵∠B=∠1(已知)
∴____//____( )
(2)∵CG // DF(已知)
∴∠2= ( )
(3)∵∠3=∠A(已知)
∴____//____( )
(4)∵AG // DF(已知)
∴∠3=_____( )
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
基础练习
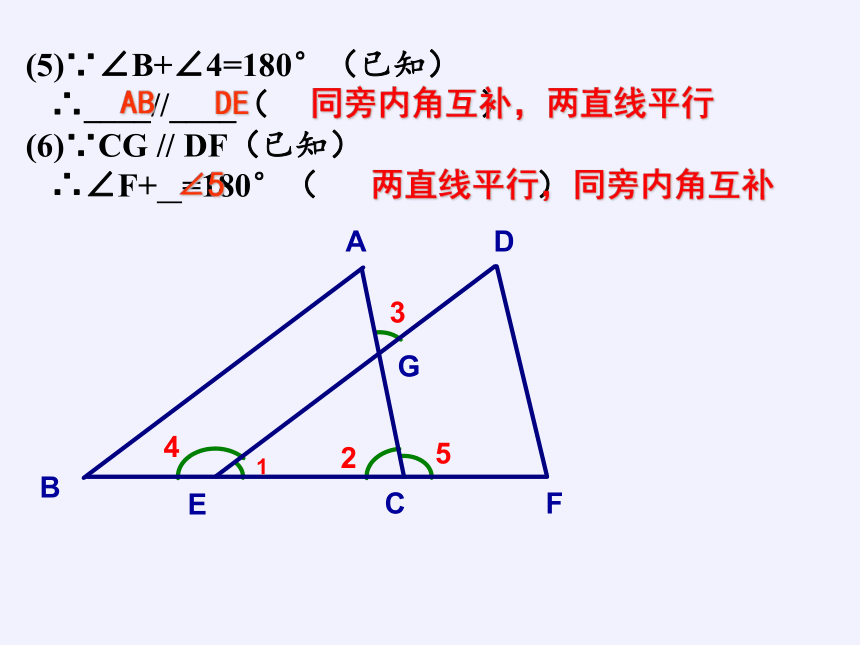
(5)∵∠B+∠4=180°(已知)
∴____//____( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
同旁内角互补,两直线平行
AB
DE
∠5
两直线平行,同旁内角互补
a
b
内错角相等,两直线平行
∠4
两直线平行,同位角相等
∠5
两直线平行,同旁内角互补
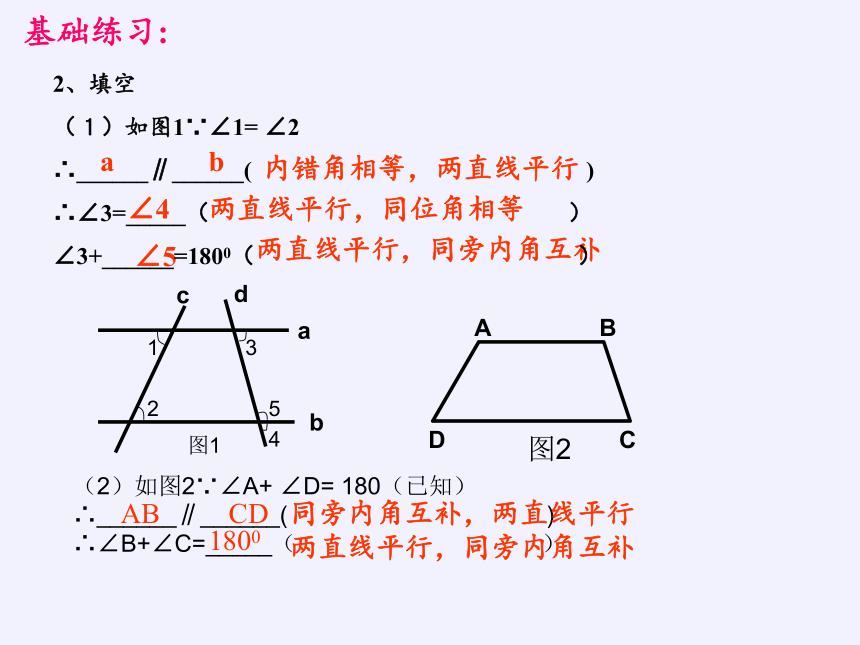
2、填空
(1)如图1∵∠1= ∠2
∴______∥______( )
∴∠3=_____( )
∠3+______=1800( )
a
b
c
d
1
2
3
4
5
图1
(2)如图2∵∠A+ ∠D= 180(已知)
∴______∥______( )
∴∠B+∠C=_____( )
A
B
D
C
图2
AB
CD
同旁内角互补,两直线平行
1800
两直线平行,同旁内角互补
基础练习:
3.如图:∠ 1=100°∠2=80°,
∠3=105° 则∠4=_______
a
b
c
d
1
2
3
4
4. 两条直线被第三条直线所截,则( )
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
基础练习:
105°
D
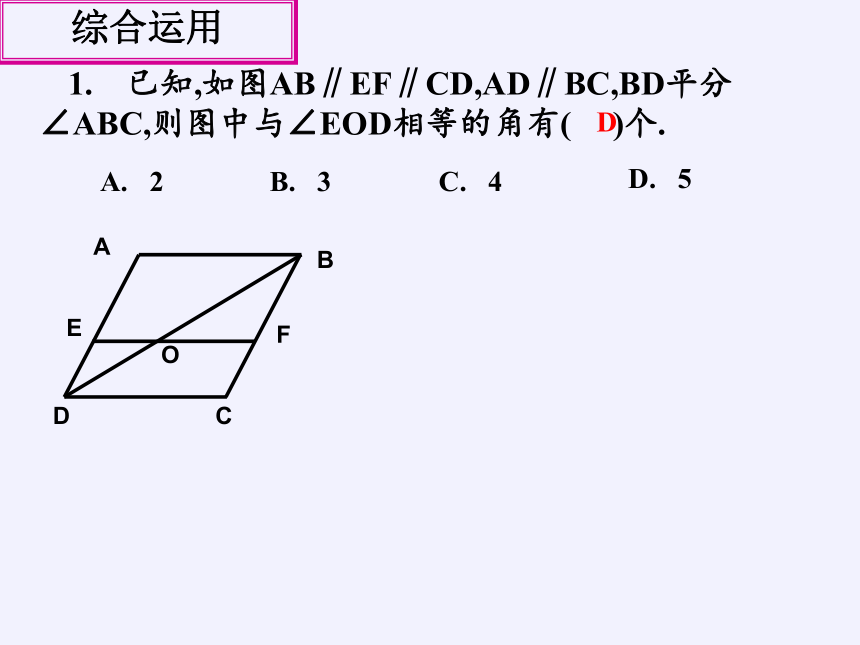
1. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
综合运用
例1、如图:添加什么条件时,可以判定DE∥ BC 为什么
综合运用
例2、如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
A
E
D
F
B
C
综合运用
变式1:已知,如图,AB∥CD,BE平分∠ABC,CF平分
∠BCD,你能发现∠1与∠2的关系吗?说明理由.
1
2
例3:如图,∠1=∠2,BE平分∠ABC,CF平分
∠BCD,你能发现AB与CD的位置关系吗?说明理由.
综合运用
变式2:如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
F
D
C
A
B
E
1
2
综合运用
例4:已知:如图,∠AGD=∠ACB,∠1=∠2,
CD与EF平行吗?为什么?
变式1:已知:如图CD⊥AB,
EF⊥AB,∠1=∠2,
那么 GD与BC平行吗?为什么?
A
G
C
F
B
E
D
1
2
3
变式2:已知:如图,CD∥EF,GD∥ BC,
那么∠1=∠2吗?为什么?
例5:如图,AB∥CD,∠B=120°,∠D=130°,
求∠BED的度数。
1
2
综合运用
F
变式1:如图,AB∥CD,∠B=20°,∠D=30°,
求∠BED的度数。
A
B
C
D
E
F
A
B
C
D
E
E
变式2:如图AB∥CD,∠B=20°,∠D=65°,
求∠BED的度数。
F
A
B
C
D
E
A
B
C
D
拓展
如图,AB∥CD, 试找出∠AEC 、∠A、∠C之间的关系。
拓展
1:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
2:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
1
2
A
B
C
D
E
F
A
B
C
D
E
E
拓展
1:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
拓展
3:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
F
A
B
C
D
E
E
如图,直线EF过点A, D是BA延长线上的点 ,具备什么条件时,可以判定EF BC 为什么
B
C
E
F
D
A
一题多解:
1
2
A
D
B
E
1
2
C
例题精讲:
例2 如图,已知:AC∥DE,∠1=∠2,试说明AB∥CD.
如图给出下列论断: (1)AB//CD (2)AD//BC (3)∠A=∠C
以上,其中两个作为题设,另一个作为结论,用 “如果……,
那么……”的形式,写出一个你认为正确的命题。
A
B
C
D
探究创新:
例1、如图,已知B,E分别是线段AC,DF
上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
例2、如图所示,把一张长方形纸片
ABCD沿EF折叠后,点C,D分别
落在C′,D′的位置上,EC′交AD
于点G,已知∠EFG=58°,
求∠BEG度数.
例3如图,EF∥AD,∠1 =∠2,
∠BAC = 70°,求∠AGD。
例 4如图,已知∠B=∠C,AD∥BC,
试说明AD平分∠CAE.
例题精讲:
例1:如图所示,已知DE∥BC,∠1=∠2,试说明CD是∠ECB的平分线.
举一反三 如图,已知AB∥CD,
EF交AB于点H,交CD于点G,
试判断∠1与∠2是否相等.
例2 如图,已知∠1=∠2,∠3=∠4,∠5=∠C,证明:AB∥DE.
举一反三 如图所示,已知∠1+∠2=180°,
∠A=∠C,AD平分∠BDF,
求证:∠EBC=∠DBC.
例3 如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=50,∠B=76°,求∠EDC及∠CDB的度数.
谢 谢
7.2 探索平行线的性质
学习目标
1、掌握平行线的判定和性质,
以及它们的区别;
2、能熟练、准确、灵活地应用
平行线的判定和性质解决问题。
知识梳理
一、平行线的性质
1、两直线平行,同位角相等
2、两直线平行,内错角相等
3、两直线平行,同旁内角互补
二、平行线的判定
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
1.如图,填空
(1)∵∠B=∠1(已知)
∴____//____( )
(2)∵CG // DF(已知)
∴∠2= ( )
(3)∵∠3=∠A(已知)
∴____//____( )
(4)∵AG // DF(已知)
∴∠3=_____( )
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
基础练习
(5)∵∠B+∠4=180°(已知)
∴____//____( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
同旁内角互补,两直线平行
AB
DE
∠5
两直线平行,同旁内角互补
a
b
内错角相等,两直线平行
∠4
两直线平行,同位角相等
∠5
两直线平行,同旁内角互补
2、填空
(1)如图1∵∠1= ∠2
∴______∥______( )
∴∠3=_____( )
∠3+______=1800( )
a
b
c
d
1
2
3
4
5
图1
(2)如图2∵∠A+ ∠D= 180(已知)
∴______∥______( )
∴∠B+∠C=_____( )
A
B
D
C
图2
AB
CD
同旁内角互补,两直线平行
1800
两直线平行,同旁内角互补
基础练习:
3.如图:∠ 1=100°∠2=80°,
∠3=105° 则∠4=_______
a
b
c
d
1
2
3
4
4. 两条直线被第三条直线所截,则( )
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
基础练习:
105°
D
1. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
综合运用
例1、如图:添加什么条件时,可以判定DE∥ BC 为什么
综合运用
例2、如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
A
E
D
F
B
C
综合运用
变式1:已知,如图,AB∥CD,BE平分∠ABC,CF平分
∠BCD,你能发现∠1与∠2的关系吗?说明理由.
1
2
例3:如图,∠1=∠2,BE平分∠ABC,CF平分
∠BCD,你能发现AB与CD的位置关系吗?说明理由.
综合运用
变式2:如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
F
D
C
A
B
E
1
2
综合运用
例4:已知:如图,∠AGD=∠ACB,∠1=∠2,
CD与EF平行吗?为什么?
变式1:已知:如图CD⊥AB,
EF⊥AB,∠1=∠2,
那么 GD与BC平行吗?为什么?
A
G
C
F
B
E
D
1
2
3
变式2:已知:如图,CD∥EF,GD∥ BC,
那么∠1=∠2吗?为什么?
例5:如图,AB∥CD,∠B=120°,∠D=130°,
求∠BED的度数。
1
2
综合运用
F
变式1:如图,AB∥CD,∠B=20°,∠D=30°,
求∠BED的度数。
A
B
C
D
E
F
A
B
C
D
E
E
变式2:如图AB∥CD,∠B=20°,∠D=65°,
求∠BED的度数。
F
A
B
C
D
E
A
B
C
D
拓展
如图,AB∥CD, 试找出∠AEC 、∠A、∠C之间的关系。
拓展
1:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
2:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
1
2
A
B
C
D
E
F
A
B
C
D
E
E
拓展
1:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
拓展
3:如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
F
A
B
C
D
E
E
如图,直线EF过点A, D是BA延长线上的点 ,具备什么条件时,可以判定EF BC 为什么
B
C
E
F
D
A
一题多解:
1
2
A
D
B
E
1
2
C
例题精讲:
例2 如图,已知:AC∥DE,∠1=∠2,试说明AB∥CD.
如图给出下列论断: (1)AB//CD (2)AD//BC (3)∠A=∠C
以上,其中两个作为题设,另一个作为结论,用 “如果……,
那么……”的形式,写出一个你认为正确的命题。
A
B
C
D
探究创新:
例1、如图,已知B,E分别是线段AC,DF
上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
例2、如图所示,把一张长方形纸片
ABCD沿EF折叠后,点C,D分别
落在C′,D′的位置上,EC′交AD
于点G,已知∠EFG=58°,
求∠BEG度数.
例3如图,EF∥AD,∠1 =∠2,
∠BAC = 70°,求∠AGD。
例 4如图,已知∠B=∠C,AD∥BC,
试说明AD平分∠CAE.
例题精讲:
例1:如图所示,已知DE∥BC,∠1=∠2,试说明CD是∠ECB的平分线.
举一反三 如图,已知AB∥CD,
EF交AB于点H,交CD于点G,
试判断∠1与∠2是否相等.
例2 如图,已知∠1=∠2,∠3=∠4,∠5=∠C,证明:AB∥DE.
举一反三 如图所示,已知∠1+∠2=180°,
∠A=∠C,AD平分∠BDF,
求证:∠EBC=∠DBC.
例3 如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=50,∠B=76°,求∠EDC及∠CDB的度数.
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
