5.3.1 平行线的性质和判定及其综合运用2 课件(共19张PPT)
文档属性
| 名称 | 5.3.1 平行线的性质和判定及其综合运用2 课件(共19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
2022年春人教版数学
七年级下册数学精品课件
人教版 数学七年级下册
5.3.1 平行线的性质
第2课时 平行线的性质和判定及其综合运用
第五章 相交线与平行线
学习目标
1.进一步熟悉平行线的判定方法和性质;
2.运用平行线的性质和判定进行简单的推理和计算;(重点、难点)
文字叙述 符号语言 图形
相等
两直线平行
∴ a∥ b
相等
两直线平行 ∵
∴ a∥ b
互补
两直线平行
∴ a∥ b
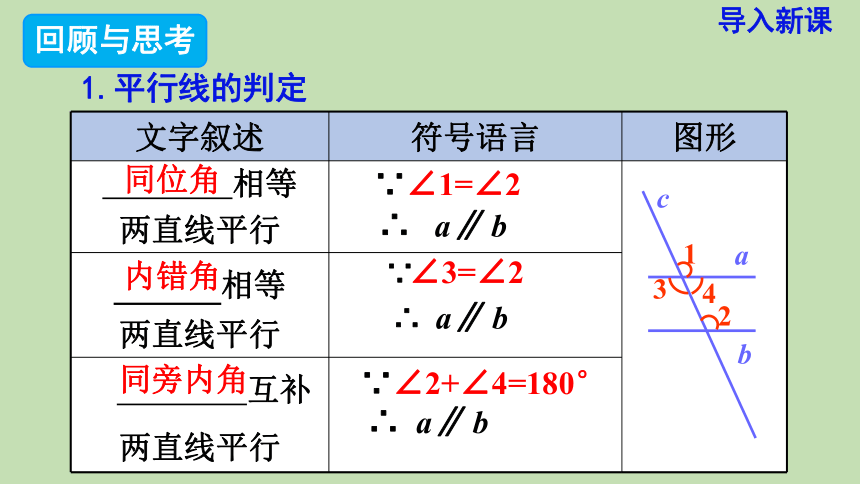
同位角
内错角
同旁内角
∵∠1=∠2
∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
导入新课
回顾与思考
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
导入新课
图形
已知
结果
依据
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
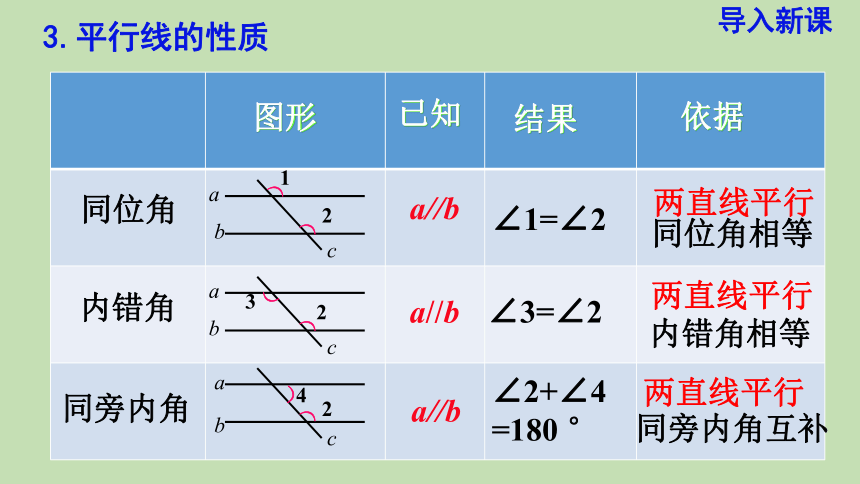
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
导入新课
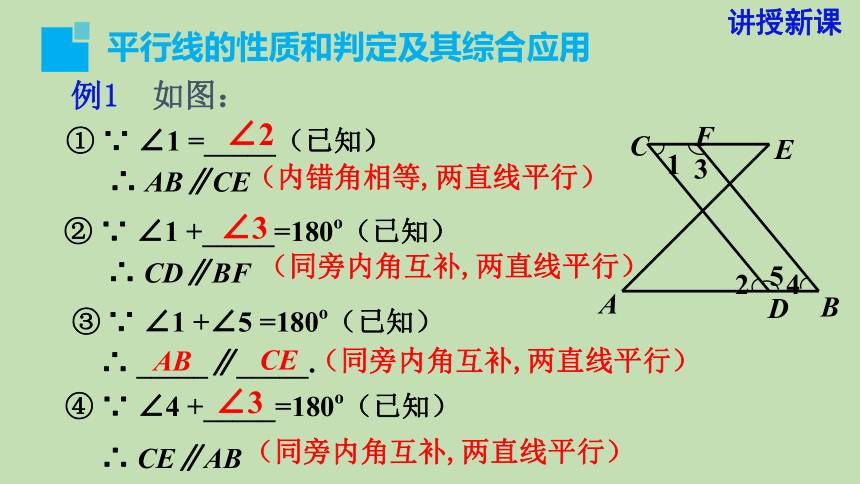
① ∵ ∠1 =_____(已知)
∴ AB∥CE
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____.
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB
∠3
∠3
例1 如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
讲授新课
平行线的性质和判定及其综合应用
例2 已知∠3=45 °,∠1与∠2互余,试说明AB//CD.
解:由于∠1与∠2是对顶角,
∴∠1=∠2.
又∵∠1+∠2=90°(已知),
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
讲授新课
解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °(等量代换).
∴∠AEC=∠1+∠2= °+ ° = °.
例3 如图,AB//CD, ∠A=100°, ∠C=110°,求∠AEC的度数.
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
讲授新课
1.填空:如图,
(1)∠1= 时,AB∥CD.
(2)∠3= 时,AD∥ BC.
D
1
2
3
4
5
A
B
C
F
E
∠2
∠5
或∠4
当堂练习
2.直线a,b与直线c相交,给出下列条件:
①∠1= ∠2; ②∠3= ∠6;
③∠4+∠7=180o; ④∠3+ ∠5=180°,
其中能判断a//b的是( )
A. ①②③④
B .①③④
C. ①③
D. ④
1
2
3
4
5
6
7
8
c
a
b
B
当堂练习
解:过点C作CF∥AB,
则 _______( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
3.已知AB∥DE,试问∠B、∠E、∠BCE有什么关系.
请完成填空:
CF∥DE
平行于同一直线的两条直线互相平行
2
两直线平行,内错角相等
∠B=∠1
两直线平行,内错角相等
A
B
C
D
E
1
2
F
当堂练习
4.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
∵∠1=∠2
∴AB∥EF
(内错角相等,两直线平行).
(已知),
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,内错角相等).
当堂练习
5.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°- 70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
当堂练习
拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠1+∠2=______;
(2)如图2,∠1+∠2+∠3=_____;
(3)如图3,∠1+∠2+∠3+∠4=_____;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n
= ;
180°
360°
540°
180°× (n-1)
A
B
C
D
1
2
B
A
E
C
D
1
2
3
B
A
E
C
D
F
1
2
4
3
B
A
E
C
D
N
1
2
n
图1
图2
图3
图4
当堂练习
判定:已知角的关系得平行的关系.
推平行,用判定.
性质:已知平行的关系得角的关系.
知平行,用性质.
平行线的“判定”与“性质”有什么不同:
课堂小结
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
七年级下册数学精品课件
人教版 数学七年级下册
5.3.1 平行线的性质
第2课时 平行线的性质和判定及其综合运用
第五章 相交线与平行线
学习目标
1.进一步熟悉平行线的判定方法和性质;
2.运用平行线的性质和判定进行简单的推理和计算;(重点、难点)
文字叙述 符号语言 图形
相等
两直线平行
∴ a∥ b
相等
两直线平行 ∵
∴ a∥ b
互补
两直线平行
∴ a∥ b
同位角
内错角
同旁内角
∵∠1=∠2
∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
导入新课
回顾与思考
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
导入新课
图形
已知
结果
依据
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
导入新课
① ∵ ∠1 =_____(已知)
∴ AB∥CE
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____.
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB
∠3
∠3
例1 如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
讲授新课
平行线的性质和判定及其综合应用
例2 已知∠3=45 °,∠1与∠2互余,试说明AB//CD.
解:由于∠1与∠2是对顶角,
∴∠1=∠2.
又∵∠1+∠2=90°(已知),
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
讲授新课
解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °(等量代换).
∴∠AEC=∠1+∠2= °+ ° = °.
例3 如图,AB//CD, ∠A=100°, ∠C=110°,求∠AEC的度数.
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
讲授新课
1.填空:如图,
(1)∠1= 时,AB∥CD.
(2)∠3= 时,AD∥ BC.
D
1
2
3
4
5
A
B
C
F
E
∠2
∠5
或∠4
当堂练习
2.直线a,b与直线c相交,给出下列条件:
①∠1= ∠2; ②∠3= ∠6;
③∠4+∠7=180o; ④∠3+ ∠5=180°,
其中能判断a//b的是( )
A. ①②③④
B .①③④
C. ①③
D. ④
1
2
3
4
5
6
7
8
c
a
b
B
当堂练习
解:过点C作CF∥AB,
则 _______( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
3.已知AB∥DE,试问∠B、∠E、∠BCE有什么关系.
请完成填空:
CF∥DE
平行于同一直线的两条直线互相平行
2
两直线平行,内错角相等
∠B=∠1
两直线平行,内错角相等
A
B
C
D
E
1
2
F
当堂练习
4.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
∵∠1=∠2
∴AB∥EF
(内错角相等,两直线平行).
(已知),
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,内错角相等).
当堂练习
5.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°- 70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
当堂练习
拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠1+∠2=______;
(2)如图2,∠1+∠2+∠3=_____;
(3)如图3,∠1+∠2+∠3+∠4=_____;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n
= ;
180°
360°
540°
180°× (n-1)
A
B
C
D
1
2
B
A
E
C
D
1
2
3
B
A
E
C
D
F
1
2
4
3
B
A
E
C
D
N
1
2
n
图1
图2
图3
图4
当堂练习
判定:已知角的关系得平行的关系.
推平行,用判定.
性质:已知平行的关系得角的关系.
知平行,用性质.
平行线的“判定”与“性质”有什么不同:
课堂小结
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
