高三周练1(Word含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
高三周练1
1.(2021·浙江·模拟预测)已知是虚数单位,若复数,则( )
A.-0.5 B. C.0.5 D.
【答案】D【解析】由题意可知,,,
故,,
所以,
2.(2022·浙江·模拟预测)设,若二项式的展开式中第二项的系数是1,则二项式的展开式中第三项的系数是( )
A. B.1 C. D.5
【答案】C【解析】由二项式的展开式中第二项,
所以,
二项式的展开式中第三项,
所以.
3.(2022·浙江温州·高三开学考试)已知随机变量X的分布列是:
若,则( )A. B. C. D.
【答案】C【解析】由已知可得,解得,
因此,.
4.(2022·浙江·高三专题练习)设X为随机变量,,若随机变量X的期望为4,则( )
A. B. C. D.
【答案】D【解析】由题知,解得,所以,
5.(2017·浙江·模拟预测)已知平面,直线、,若,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】D【解析】若,且,则或,即“”“”;
若,且,则或、异面,则“”“”.
因此,“”是“”的既不充分也不必要条件.
6.(2021·浙江·海亮高级中学模拟预测)已知(为虚数单位),则复数的模为( )
A. B.4 C.5 D.
【答案】C【解析】,所以,故,.
7.(2021·浙江·绍兴市柯桥区教师发展中心模拟预测)已知,若复数(是虚数单位)是纯虚数,则( )
A.0 B.1 C. D.2
【答案】C【解析】是纯虚数,则,解得,
8.(2022·浙江·镇海中学高二期末)的展开式中的系数是( )
A.1792 B. C.448 D.
【答案】D的展开式中,含的项为.
所以的系数是.
9.(2022·浙江·模拟预测)已知,(为虚数单位)是纯虚数,则a,b应满足( )
A.b=-2a B.b=a C.ab=1 D.ab=0
【答案】A【解析】,
因为(为虚数单位)是纯虚数,所以,且b-2a≠0,解得:b=-2a.
10.(2021·浙江·模拟预测)已知复数满足(是虚数单位),则复数的共轭复数为( )
A. B.
C. D.
【答案】B【详解】由已知可得,因此,.
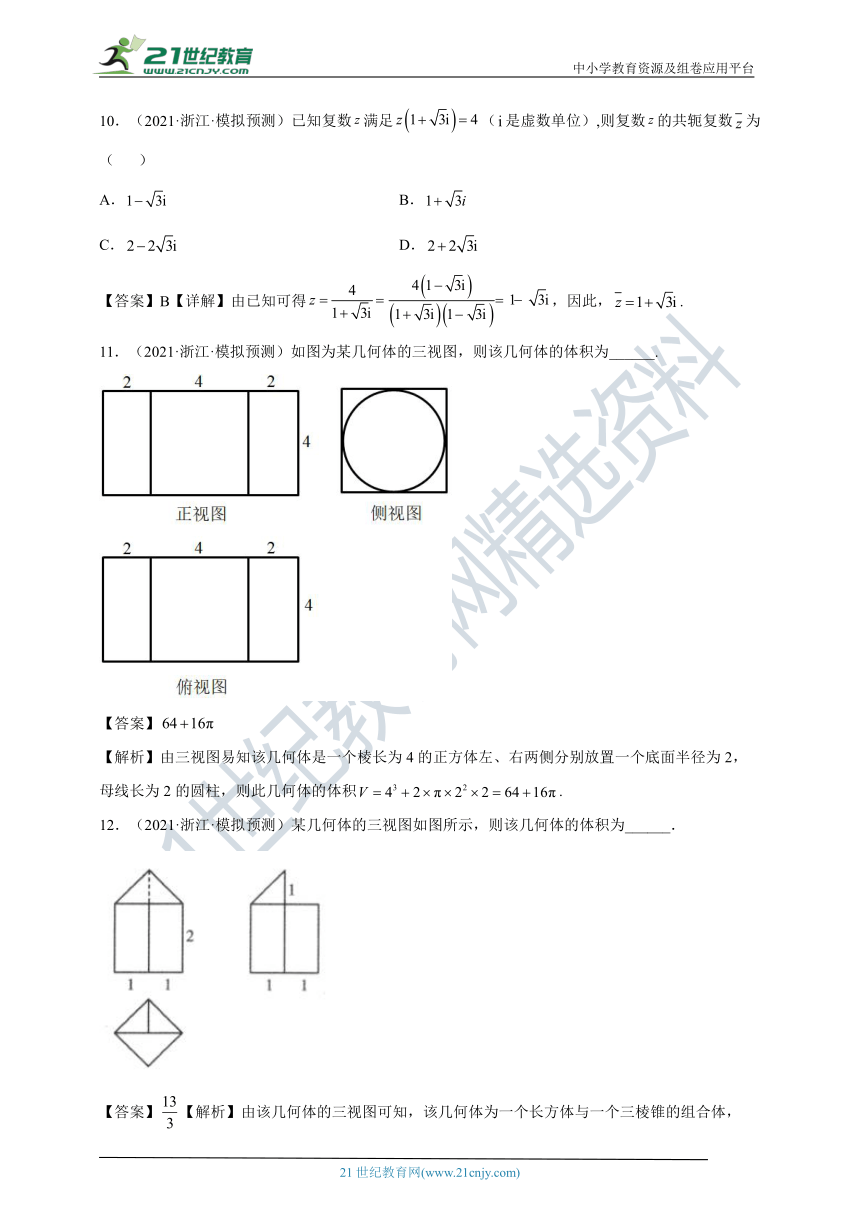
11.(2021·浙江·模拟预测)如图为某几何体的三视图,则该几何体的体积为______.
【答案】
【解析】由三视图易知该几何体是一个棱长为4的正方体左、右两侧分别放置一个底面半径为2,
母线长为2的圆柱,则此几何体的体积.
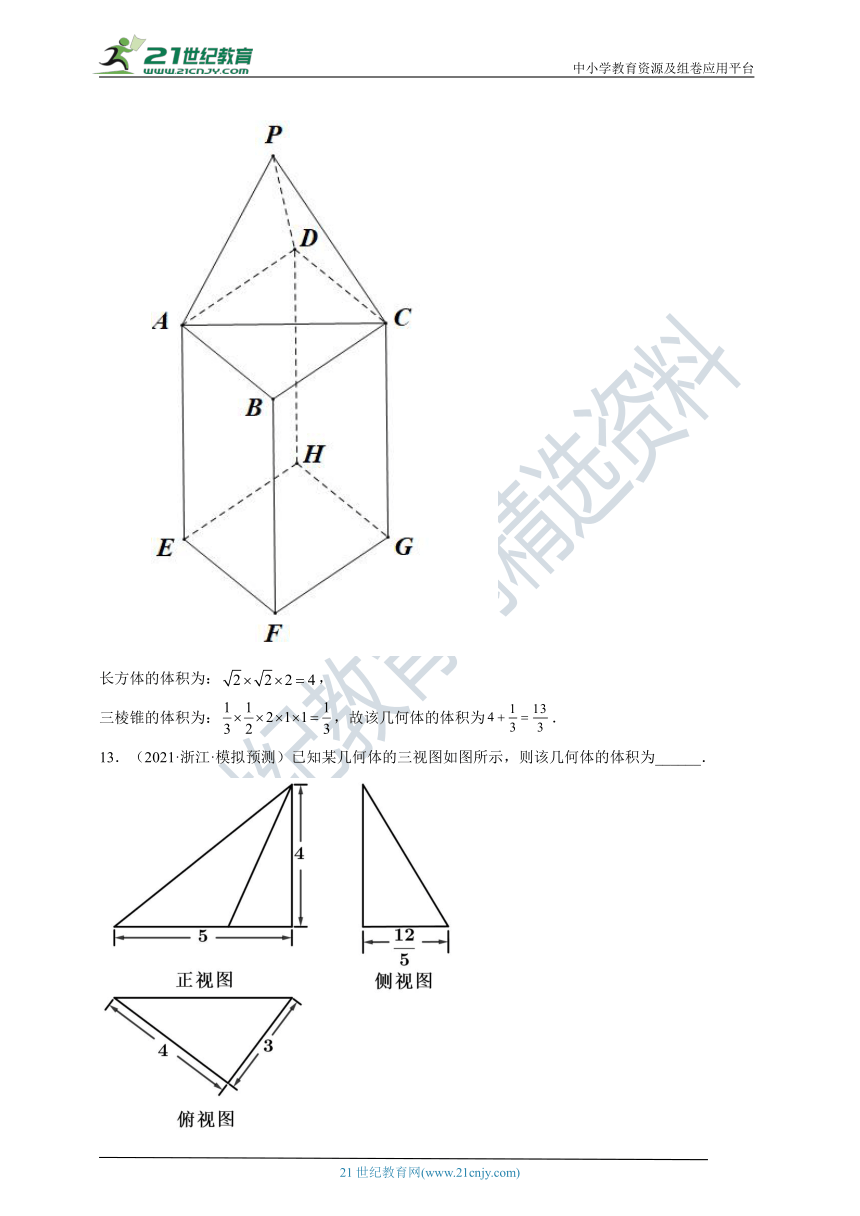
12.(2021·浙江·模拟预测)某几何体的三视图如图所示,则该几何体的体积为______.
【答案】【解析】由该几何体的三视图可知,该几何体为一个长方体与一个三棱锥的组合体,
长方体的体积为:,
三棱锥的体积为:,故该几何体的体积为.
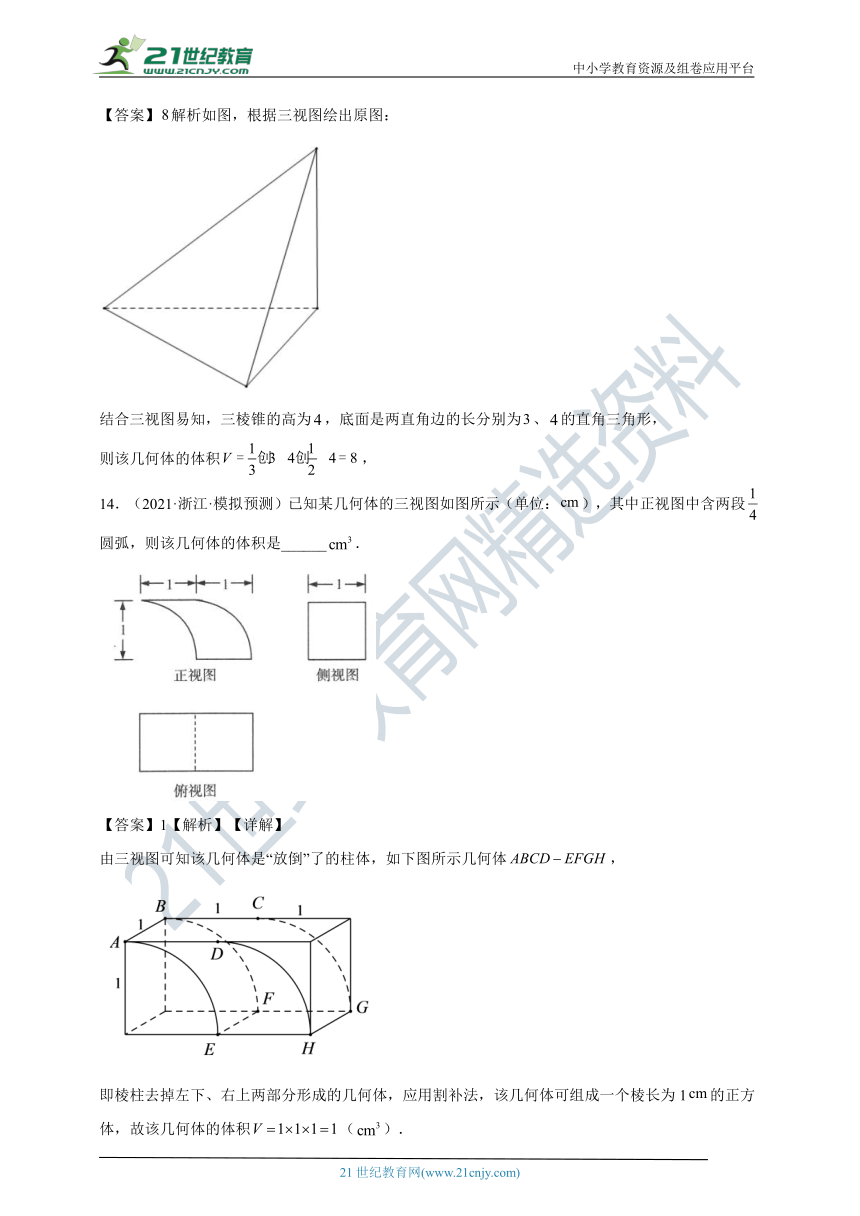
13.(2021·浙江·模拟预测)已知某几何体的三视图如图所示,则该几何体的体积为______.
【答案】解析如图,根据三视图绘出原图:
结合三视图易知,三棱锥的高为,底面是两直角边的长分别为、的直角三角形,
则该几何体的体积,
14.(2021·浙江·模拟预测)已知某几何体的三视图如图所示(单位:),其中正视图中含两段圆弧,则该几何体的体积是______.
【答案】1【解析】【详解】
由三视图可知该几何体是“放倒”了的柱体,如下图所示几何体,
即棱柱去掉左下、右上两部分形成的几何体,应用割补法,该几何体可组成一个棱长为1的正方体,故该几何体的体积().
15.(2022·浙江·模拟预测)已知,则___,___.
【答案】 ## ##0.8
【解析】
16.(2022·浙江上虞·高三期末)在的展开式中,若,则含项的系数是____________;若常数项是24,则____________.
【答案】 -80 4【详解】
时,的展开式的通项公式为:
,其中 ,
令 ,则 ,故 ,
即含项的系数是 ;
的展开式的通项公式为,
其中,
令,则 ,
由常数项为24可得: ,解得n=4,
17.(2022·浙江绍兴·高三期末)袋子中有3个白球,2个红球,现从中有放回地随机取2个球,每次取1个,且各次取球间相互独立.设此过程中取到的红球个数为,则__________,__________.
【答案】 【解析】有放回地取球,每次取一球,则每次取到红球的概率为
在此过程中取到的红球个数为,的取值为0,1,2.
则,则
18.(2022·浙江上虞·高三期末)已知随机变量的分布列如下:且,则实数____________,若随机变量,则____________.
2 3 4
【答案】 ##
【解析】由题意得,解得,
所以,
所以,
19.(2021·浙江·模拟预测)在平面直角坐标系中,若角的终边在直线上,则=________,________.
【答案】 1 0【解析】可设角的终边上的点为,
则,
.
20.(2021·浙江·模拟预测)已知,且,则___________,____________.
【答案】
【解析】【详解】
,
又,,
.
21.(2022·浙江温州·高三开学考试)二项式的展开式中,只有第项的二项式系数最大,则__________,含的项的系数是__________.
【答案】
【解析】【详解】二项式的展开式中,只有第项的二项式系数最大,则展开式中共有项,
则,可得,
的展开式通项为,
令,可得,因此,展开式中含的项的系数是.
22.(2022·浙江·模拟预测)二项式的展开式中,二项式系数最大的项是第___项,常数项是___.
【答案】
【解析】因为二项式的展开式共有项,所以二项式系数最大为,所以二项式系数最大的项是第项;二项式的展开式的通项公式为,令,所以常数项为.
23.(2022·浙江·慈溪中学高三阶段练习)已知,.若,则_________;_________.
【答案】 2 40
【解析】【详解】∵
令,得,
,
∴,
所以含项系数为.
24.(2022·浙江·模拟预测)在二项式的展开式中,常数项是___,系数最大的项是___.
【答案】 【解析】,
因此,展开式中的常数项是,系数最大的项为.
25.(2022·浙江·高三期末)已知二项式的展开式中,第4项的系数为-32,则n=___________,常数项为___________.
【答案】 4; 24.【详解】
由二项式展开式的通项公式,
得二项式的通项公式为,
所以,
则,得,
即,
所以的常数项为.
26.(2022·浙江绍兴·高三期末)在的展开式中,常数项为__________,的系数是__________.
【答案】 【详解】
∵,
∴展开式中的常数项为,的系数是.
27.(2021·浙江·高三开学考试)从装有除颜色外完全相同的个白球和4个黑球的布袋中随机摸取一球,有放回的摸取3次,记摸得白球个数为,若,则___________,___________.
【答案】 2
【解析】【详解】由题意,,
因为,所以,解得,
所以.
28.(2022·浙江·高三专题练习)袋中装有大小相同的个红球和个黄球,小明无放回地连续摸取次,每次从中摸取个.记摸到红球的个数为,则______,______
【答案】
【解析】【详解】随机变量的可能取值有、,则,,
所以,.
29.(2021·浙江省三门中学高三期中)已知袋内有大小相同的1个红球和3个白球,袋内有大小相同的1个红球和2个白球.现从 两个袋内各任取2个球,则恰好有1个红球的概率为___________.记取出的4个球中红球的个数为随机变量,则的数学期望为___________.
【答案】
【解析】【详解】恰好有1个红球的概率,
取出的4个球中红球的个数的可能取值为:,
,
,
,
分布列如下表:
期望,
故答案为:,.
30.(2021·浙江·二模)在△ABC中,角A,B,C所对的边分别为a,b,c.
(1)若1+2cosAcosB=2sinAsinB,求角C;
(2)若,求角C.
【答案】(1)(2)
【解析】(1)若1+2cosAcosB=2sinAsinB,
则cosAcosB﹣sinAsinB=,即故,
即,
所以,由 ,故
(2)若,显然,
所以,
又由tanA≠0得到tanC=﹣1,,故.
31.(2021·浙江·模拟预测)在锐角中,内角的对边分别为,且.
(1)求角的大小;
(2)求的取值范围.
【答案】(1)(2)
【解析】【小问1详解】解:,,
或,
又是锐角三角形 ,;
【小问2详解】解:由(1)可知,
,
是锐角三角形,,
,
,即.
32.(2021·浙江嘉兴·模拟预测)已知函数.
(1)求的单调递增区间;
(2)设,且,求的值.
【答案】(1);(2).
【解析】(1)因为,
由,解得,
因此,函数的单调递增区间为;
(2),可得,
因为,则,所以,,
因此,.
33.(2022·浙江·高三开学考试)已知函数的部分图象如图所示,图象与轴交于点.
(1)求函数的最小正周期及,的值;
(2)已知,,求的值,
【答案】(1)最小正周期, ,
(2)
【解析】(1)的最小正周期,
∵为最大值,则,,
而,故取,
∵函数图象过,∴,
(2),
∵,∴,∴,∴,
∴.
34.(2022·浙江·高三期末)已知函数.
(1)求函数的单调递增区间;
(2)已知,若函数在区间[0,]上恰好有两个零点,求a的取值范围.
【答案】(1)(2)
【解析】(1)
由可得,
即函数的单调递增区间为
(2),,令
函数在区间[0,]上恰好有两个零点
函数与只有两个交点
由图象可知,
35.(2022·浙江·模拟预测)如图,在四棱锥中,底面ABCD是菱形.其中,且.
(1)证明:;(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
【解析】(1)由题设,,即△为等边三角形,若为中点,连接,
所以,又且底面ABCD是菱形,即,
则,故,即,
又,可得面,又面,则,
由,则.
(2)若,由知:,
由(1)结论知:,而,
所以,在面上过作,又面,面,则,,构建如下图示的空间直角坐标系,
则,故,,,
若是面的法向量,则,令,则,
若是面的法向量,则,令,则,
所以,故钝二面角的余弦值为.
36.(2021·浙江·海亮高级中学模拟预测)如图,在四棱锥中,底面为矩形.平面,,当分别为的中点.
(1)求证:平面;
(2)若且,平面与平面所成锐二面角的余弦值为,求直线与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】(1)证明:,为中点,,
四边形为矩形,,
又平面平面,,
又平面,
平面,平面,,
分别的中点,,
又平面,
平面;
(2)显然两两垂直,以为坐标原点,所在直线分别为轴、轴、轴,建立如图所示坐标系,
,,
设平面的一个法向量为,平面的一个法向量为,
则,,
由题意得,,解得,
,
设直线与平面所成的角为,
则.
37.(2021·浙江·绍兴市柯桥区教师发展中心模拟预测)设函数.
(1)求函数的最小正周期;
(2)求函数在上的最小值.
【答案】(1)(2)
【解析】(1)解:函数,
所以.
故函数的最小正周期;
(2)解:由于,所以,
所以
即;
由于,所以,所以,
故,
当,即时,函数取得最小值为.
38.(2022·浙江·模拟预测)已知函数.
(1)求f(x)的最小正周期和在的单调递增区间;
(2)已知,先化简后计算求值:
【答案】(1)(2)1
【解(1)
,即,
所以最小正周期为,
当,时,函数单调递增,
即函数单调递增区间为,
所以f(x)在的单调递增区间.
(2)
已知,,即,
,所以,解得:.
所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
高三周练1
1.(2021·浙江·模拟预测)已知是虚数单位,若复数,则( )
A.-0.5 B. C.0.5 D.
【答案】D【解析】由题意可知,,,
故,,
所以,
2.(2022·浙江·模拟预测)设,若二项式的展开式中第二项的系数是1,则二项式的展开式中第三项的系数是( )
A. B.1 C. D.5
【答案】C【解析】由二项式的展开式中第二项,
所以,
二项式的展开式中第三项,
所以.
3.(2022·浙江温州·高三开学考试)已知随机变量X的分布列是:
若,则( )A. B. C. D.
【答案】C【解析】由已知可得,解得,
因此,.
4.(2022·浙江·高三专题练习)设X为随机变量,,若随机变量X的期望为4,则( )
A. B. C. D.
【答案】D【解析】由题知,解得,所以,
5.(2017·浙江·模拟预测)已知平面,直线、,若,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】D【解析】若,且,则或,即“”“”;
若,且,则或、异面,则“”“”.
因此,“”是“”的既不充分也不必要条件.
6.(2021·浙江·海亮高级中学模拟预测)已知(为虚数单位),则复数的模为( )
A. B.4 C.5 D.
【答案】C【解析】,所以,故,.
7.(2021·浙江·绍兴市柯桥区教师发展中心模拟预测)已知,若复数(是虚数单位)是纯虚数,则( )
A.0 B.1 C. D.2
【答案】C【解析】是纯虚数,则,解得,
8.(2022·浙江·镇海中学高二期末)的展开式中的系数是( )
A.1792 B. C.448 D.
【答案】D的展开式中,含的项为.
所以的系数是.
9.(2022·浙江·模拟预测)已知,(为虚数单位)是纯虚数,则a,b应满足( )
A.b=-2a B.b=a C.ab=1 D.ab=0
【答案】A【解析】,
因为(为虚数单位)是纯虚数,所以,且b-2a≠0,解得:b=-2a.
10.(2021·浙江·模拟预测)已知复数满足(是虚数单位),则复数的共轭复数为( )
A. B.
C. D.
【答案】B【详解】由已知可得,因此,.
11.(2021·浙江·模拟预测)如图为某几何体的三视图,则该几何体的体积为______.
【答案】
【解析】由三视图易知该几何体是一个棱长为4的正方体左、右两侧分别放置一个底面半径为2,
母线长为2的圆柱,则此几何体的体积.
12.(2021·浙江·模拟预测)某几何体的三视图如图所示,则该几何体的体积为______.
【答案】【解析】由该几何体的三视图可知,该几何体为一个长方体与一个三棱锥的组合体,
长方体的体积为:,
三棱锥的体积为:,故该几何体的体积为.
13.(2021·浙江·模拟预测)已知某几何体的三视图如图所示,则该几何体的体积为______.
【答案】解析如图,根据三视图绘出原图:
结合三视图易知,三棱锥的高为,底面是两直角边的长分别为、的直角三角形,
则该几何体的体积,
14.(2021·浙江·模拟预测)已知某几何体的三视图如图所示(单位:),其中正视图中含两段圆弧,则该几何体的体积是______.
【答案】1【解析】【详解】
由三视图可知该几何体是“放倒”了的柱体,如下图所示几何体,
即棱柱去掉左下、右上两部分形成的几何体,应用割补法,该几何体可组成一个棱长为1的正方体,故该几何体的体积().
15.(2022·浙江·模拟预测)已知,则___,___.
【答案】 ## ##0.8
【解析】
16.(2022·浙江上虞·高三期末)在的展开式中,若,则含项的系数是____________;若常数项是24,则____________.
【答案】 -80 4【详解】
时,的展开式的通项公式为:
,其中 ,
令 ,则 ,故 ,
即含项的系数是 ;
的展开式的通项公式为,
其中,
令,则 ,
由常数项为24可得: ,解得n=4,
17.(2022·浙江绍兴·高三期末)袋子中有3个白球,2个红球,现从中有放回地随机取2个球,每次取1个,且各次取球间相互独立.设此过程中取到的红球个数为,则__________,__________.
【答案】 【解析】有放回地取球,每次取一球,则每次取到红球的概率为
在此过程中取到的红球个数为,的取值为0,1,2.
则,则
18.(2022·浙江上虞·高三期末)已知随机变量的分布列如下:且,则实数____________,若随机变量,则____________.
2 3 4
【答案】 ##
【解析】由题意得,解得,
所以,
所以,
19.(2021·浙江·模拟预测)在平面直角坐标系中,若角的终边在直线上,则=________,________.
【答案】 1 0【解析】可设角的终边上的点为,
则,
.
20.(2021·浙江·模拟预测)已知,且,则___________,____________.
【答案】
【解析】【详解】
,
又,,
.
21.(2022·浙江温州·高三开学考试)二项式的展开式中,只有第项的二项式系数最大,则__________,含的项的系数是__________.
【答案】
【解析】【详解】二项式的展开式中,只有第项的二项式系数最大,则展开式中共有项,
则,可得,
的展开式通项为,
令,可得,因此,展开式中含的项的系数是.
22.(2022·浙江·模拟预测)二项式的展开式中,二项式系数最大的项是第___项,常数项是___.
【答案】
【解析】因为二项式的展开式共有项,所以二项式系数最大为,所以二项式系数最大的项是第项;二项式的展开式的通项公式为,令,所以常数项为.
23.(2022·浙江·慈溪中学高三阶段练习)已知,.若,则_________;_________.
【答案】 2 40
【解析】【详解】∵
令,得,
,
∴,
所以含项系数为.
24.(2022·浙江·模拟预测)在二项式的展开式中,常数项是___,系数最大的项是___.
【答案】 【解析】,
因此,展开式中的常数项是,系数最大的项为.
25.(2022·浙江·高三期末)已知二项式的展开式中,第4项的系数为-32,则n=___________,常数项为___________.
【答案】 4; 24.【详解】
由二项式展开式的通项公式,
得二项式的通项公式为,
所以,
则,得,
即,
所以的常数项为.
26.(2022·浙江绍兴·高三期末)在的展开式中,常数项为__________,的系数是__________.
【答案】 【详解】
∵,
∴展开式中的常数项为,的系数是.
27.(2021·浙江·高三开学考试)从装有除颜色外完全相同的个白球和4个黑球的布袋中随机摸取一球,有放回的摸取3次,记摸得白球个数为,若,则___________,___________.
【答案】 2
【解析】【详解】由题意,,
因为,所以,解得,
所以.
28.(2022·浙江·高三专题练习)袋中装有大小相同的个红球和个黄球,小明无放回地连续摸取次,每次从中摸取个.记摸到红球的个数为,则______,______
【答案】
【解析】【详解】随机变量的可能取值有、,则,,
所以,.
29.(2021·浙江省三门中学高三期中)已知袋内有大小相同的1个红球和3个白球,袋内有大小相同的1个红球和2个白球.现从 两个袋内各任取2个球,则恰好有1个红球的概率为___________.记取出的4个球中红球的个数为随机变量,则的数学期望为___________.
【答案】
【解析】【详解】恰好有1个红球的概率,
取出的4个球中红球的个数的可能取值为:,
,
,
,
分布列如下表:
期望,
故答案为:,.
30.(2021·浙江·二模)在△ABC中,角A,B,C所对的边分别为a,b,c.
(1)若1+2cosAcosB=2sinAsinB,求角C;
(2)若,求角C.
【答案】(1)(2)
【解析】(1)若1+2cosAcosB=2sinAsinB,
则cosAcosB﹣sinAsinB=,即故,
即,
所以,由 ,故
(2)若,显然,
所以,
又由tanA≠0得到tanC=﹣1,,故.
31.(2021·浙江·模拟预测)在锐角中,内角的对边分别为,且.
(1)求角的大小;
(2)求的取值范围.
【答案】(1)(2)
【解析】【小问1详解】解:,,
或,
又是锐角三角形 ,;
【小问2详解】解:由(1)可知,
,
是锐角三角形,,
,
,即.
32.(2021·浙江嘉兴·模拟预测)已知函数.
(1)求的单调递增区间;
(2)设,且,求的值.
【答案】(1);(2).
【解析】(1)因为,
由,解得,
因此,函数的单调递增区间为;
(2),可得,
因为,则,所以,,
因此,.
33.(2022·浙江·高三开学考试)已知函数的部分图象如图所示,图象与轴交于点.
(1)求函数的最小正周期及,的值;
(2)已知,,求的值,
【答案】(1)最小正周期, ,
(2)
【解析】(1)的最小正周期,
∵为最大值,则,,
而,故取,
∵函数图象过,∴,
(2),
∵,∴,∴,∴,
∴.
34.(2022·浙江·高三期末)已知函数.
(1)求函数的单调递增区间;
(2)已知,若函数在区间[0,]上恰好有两个零点,求a的取值范围.
【答案】(1)(2)
【解析】(1)
由可得,
即函数的单调递增区间为
(2),,令
函数在区间[0,]上恰好有两个零点
函数与只有两个交点
由图象可知,
35.(2022·浙江·模拟预测)如图,在四棱锥中,底面ABCD是菱形.其中,且.
(1)证明:;(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
【解析】(1)由题设,,即△为等边三角形,若为中点,连接,
所以,又且底面ABCD是菱形,即,
则,故,即,
又,可得面,又面,则,
由,则.
(2)若,由知:,
由(1)结论知:,而,
所以,在面上过作,又面,面,则,,构建如下图示的空间直角坐标系,
则,故,,,
若是面的法向量,则,令,则,
若是面的法向量,则,令,则,
所以,故钝二面角的余弦值为.
36.(2021·浙江·海亮高级中学模拟预测)如图,在四棱锥中,底面为矩形.平面,,当分别为的中点.
(1)求证:平面;
(2)若且,平面与平面所成锐二面角的余弦值为,求直线与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】(1)证明:,为中点,,
四边形为矩形,,
又平面平面,,
又平面,
平面,平面,,
分别的中点,,
又平面,
平面;
(2)显然两两垂直,以为坐标原点,所在直线分别为轴、轴、轴,建立如图所示坐标系,
,,
设平面的一个法向量为,平面的一个法向量为,
则,,
由题意得,,解得,
,
设直线与平面所成的角为,
则.
37.(2021·浙江·绍兴市柯桥区教师发展中心模拟预测)设函数.
(1)求函数的最小正周期;
(2)求函数在上的最小值.
【答案】(1)(2)
【解析】(1)解:函数,
所以.
故函数的最小正周期;
(2)解:由于,所以,
所以
即;
由于,所以,所以,
故,
当,即时,函数取得最小值为.
38.(2022·浙江·模拟预测)已知函数.
(1)求f(x)的最小正周期和在的单调递增区间;
(2)已知,先化简后计算求值:
【答案】(1)(2)1
【解(1)
,即,
所以最小正周期为,
当,时,函数单调递增,
即函数单调递增区间为,
所以f(x)在的单调递增区间.
(2)
已知,,即,
,所以,解得:.
所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
