2021-2022学年高一下学期数学苏教版(2019)必修第二册9.3.2平面向量的坐标表示(1)课件(12张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学苏教版(2019)必修第二册9.3.2平面向量的坐标表示(1)课件(12张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 11:08:48 | ||
图片预览





文档简介
(共12张PPT)
平面向量的坐标运算(1)
问题1:前面我们对平面向量的研究主要是从“形”的层面借助于有向线段进行的,可不可以用“数”来表示向量呢
问题情境
问题2:平面向量基本定理的内容是什么?
如果 e1 , e2是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 a ,有且只有一对实数 λ1 , λ2 使得a= λ1 e1+ λ2 e2
平面向量基本定理:
不共线的平面向量 e1 , e2 叫做这一平面内所有向量的一组基底.
向量的基底:
1.平面向量的坐标表示
问题3:分别取与x 轴、y 轴方向相同的两单位向量i 、j 能否作为基底?
O
x
y
i
j
平面内任一向量a,由平面向量基本定理知,有且仅有一对实数 x , y ,使得 a=x i+y j.
a
把(x , y)叫做向量a的(直角)坐标, 记作:a=(x , y) ,
那么i =( , )
j =( , )
0 =( , )
1 0
0 1
0 0
每一个向量 a 与数组(x,y)一一对应。
建构数学
概念理解
起点在原点的向量的坐标
就是向量终点坐标。
O
x
y
i
j
a
a
问题4:若a=x i+y j, 以原点O为起点作 ,那么 的坐标是什么, 点A的坐标
又是什么
A
(x, y)
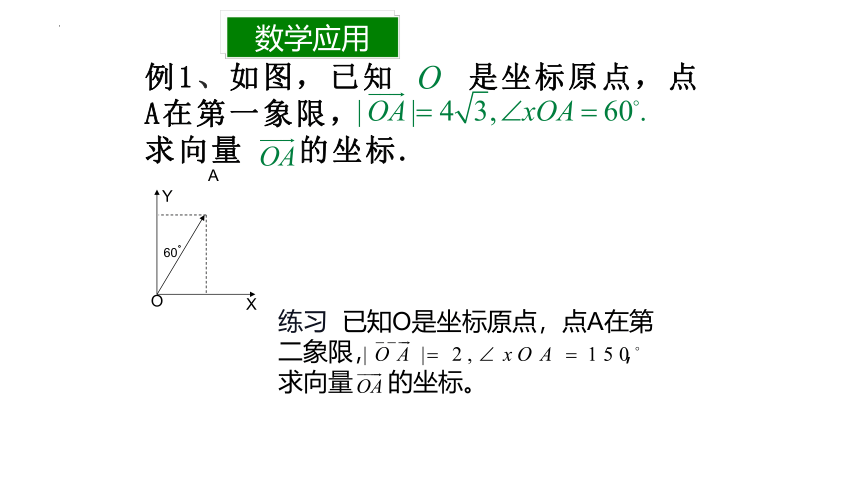
例1、如图,已知 是坐标原点,点A在第一象限, 求向量 的坐标.
O
X
Y
A
练习 已知O是坐标原点,点A在第二象限, , 求向量 的坐标。
60。
数学应用
合作探究1
已知 ,你能得出 ,
, 的坐标吗
因为 ,
所以
同理得
根据所学内容,对于起点不在坐标原点的向量,你有更好的方法表示它的坐标吗?
合作探究2
已知向量 ,且点 , ,求
的坐标.
结论:一个向量的坐标等于该向量终点的坐标减去起点的坐标.
四边形OCDA
是平行四边形?
数学应用
变式练习
已知已知平行四边形的三个顶点坐标(-2,1),(-1,3),(3,4),求第四个点使得四点构成平行四边形.
例3. 已知 平行四边形ABCD的三个顶点A、B、C的坐标分别为(-2,1)、( -1,3)、(3,4),求顶点D的坐标.
解:设顶点D的坐标为(x,y)
数学应用
谢 谢!
平面向量的坐标运算(1)
问题1:前面我们对平面向量的研究主要是从“形”的层面借助于有向线段进行的,可不可以用“数”来表示向量呢
问题情境
问题2:平面向量基本定理的内容是什么?
如果 e1 , e2是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 a ,有且只有一对实数 λ1 , λ2 使得a= λ1 e1+ λ2 e2
平面向量基本定理:
不共线的平面向量 e1 , e2 叫做这一平面内所有向量的一组基底.
向量的基底:
1.平面向量的坐标表示
问题3:分别取与x 轴、y 轴方向相同的两单位向量i 、j 能否作为基底?
O
x
y
i
j
平面内任一向量a,由平面向量基本定理知,有且仅有一对实数 x , y ,使得 a=x i+y j.
a
把(x , y)叫做向量a的(直角)坐标, 记作:a=(x , y) ,
那么i =( , )
j =( , )
0 =( , )
1 0
0 1
0 0
每一个向量 a 与数组(x,y)一一对应。
建构数学
概念理解
起点在原点的向量的坐标
就是向量终点坐标。
O
x
y
i
j
a
a
问题4:若a=x i+y j, 以原点O为起点作 ,那么 的坐标是什么, 点A的坐标
又是什么
A
(x, y)
例1、如图,已知 是坐标原点,点A在第一象限, 求向量 的坐标.
O
X
Y
A
练习 已知O是坐标原点,点A在第二象限, , 求向量 的坐标。
60。
数学应用
合作探究1
已知 ,你能得出 ,
, 的坐标吗
因为 ,
所以
同理得
根据所学内容,对于起点不在坐标原点的向量,你有更好的方法表示它的坐标吗?
合作探究2
已知向量 ,且点 , ,求
的坐标.
结论:一个向量的坐标等于该向量终点的坐标减去起点的坐标.
四边形OCDA
是平行四边形?
数学应用
变式练习
已知已知平行四边形的三个顶点坐标(-2,1),(-1,3),(3,4),求第四个点使得四点构成平行四边形.
例3. 已知 平行四边形ABCD的三个顶点A、B、C的坐标分别为(-2,1)、( -1,3)、(3,4),求顶点D的坐标.
解:设顶点D的坐标为(x,y)
数学应用
谢 谢!
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
