苏科版七年级数学下册 9.4 乘法公式(4) 课件 (共19张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 9.4 乘法公式(4) 课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 07:57:24 | ||
图片预览




文档简介
(共19张PPT)
9.4 乘法公式
a
a
b
b
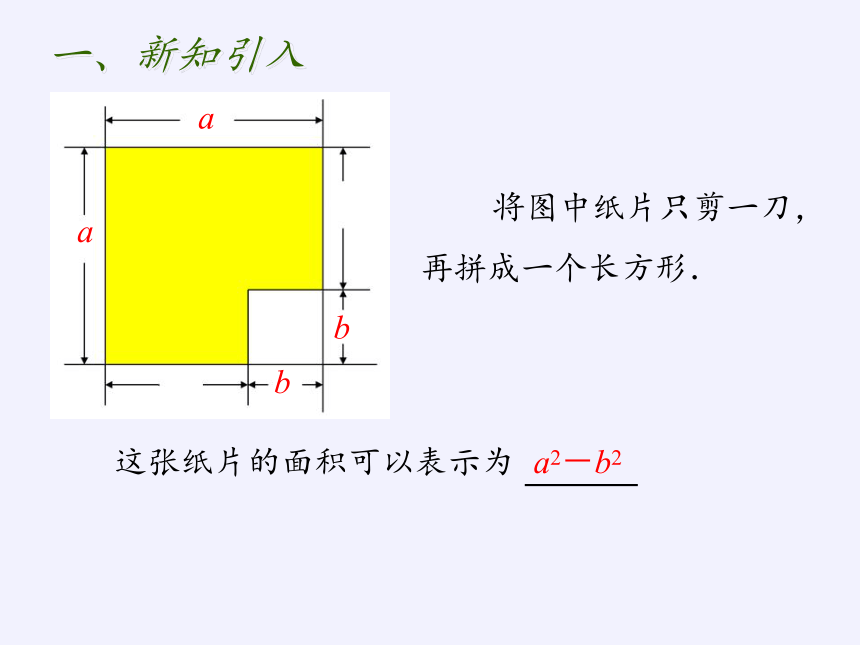
将图中纸片只剪一刀,再拼成一个长方形.
这张纸片的面积可以表示为
a2-b2
一、新知引入
a
a
b
b
a-b
a-b
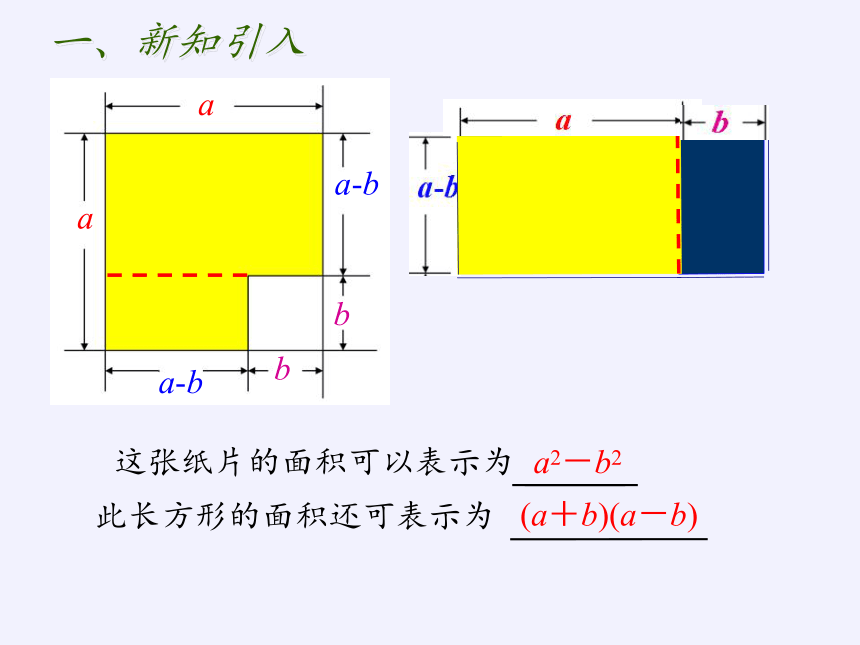
这张纸片的面积可以表示为
a2-b2
此长方形的面积还可表示为
(a+b)(a-b)
一、新知引入
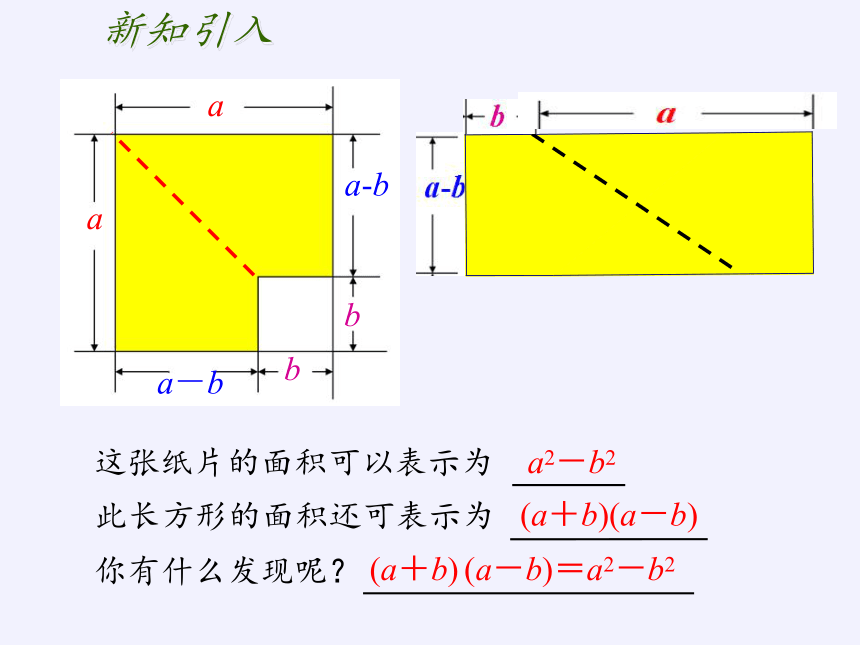
这张纸片的面积可以表示为
此长方形的面积还可表示为
(a+b)(a-b)
(a+b) (a-b)=a2-b2
你有什么发现呢?
a2-b2
a
a
b
b
a-b
a-b
新知引入
你能用多项式乘法法则说明
(a +b)(a -b)=a2-b2 的正确性吗
解:(a+b)(a-b)
=a2-ab+ba-b2
=a2-b2.
公式推导
(a +b)(a -b)=a 2-b 2
平方差公式.
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
平方差公式.
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
(a +b)(a -b)=a 2-b 2
公式特征
判断:下列各式可以利用平方差公式吗?为什么?
①
②
③
④
⑤
⑥
火眼金睛
(a +b)(a -b)=a 2-b 2
例1 用平方差公式计算:
(1)
(2)
(3)
巩固练习:
1.(1+x)(1-x) 2.(a+3b)(-3b+a)
3.(-3+2a)(-3-2a) 4.(0.5x-2y)(-2y-0.5x)
典型例题
下列计算是否正确?如有错误请改正。
(1)(x+2)(x-2)=x2-2
(2)(a+b)(b- a)=a2-b2
(3)(2x+3)(2x-3)=2x2-9
(4)(x+5)(x-6)=x2-30
(5)(-1+4b)(-1-4b)=1-16b2
×
√
b2-a2
x2-4
4x2-9
巩固提高
例2 用简便方法计算:
(1)101×99; (2)
×
巩固练习 用简便方法计算:
(1)22×18;
(2)
×
典型例题
解: 101×99
=(100+1)(100-1)
=1002-12
=10000-1
=9999
1.小组内相互列举可以运用平方差公式计算的多项式乘多项式的算式;
2.小结利用公式进行计算时容易出现的问题.
小组合作
图形面积
平方差公式
感性直观
理性推导
(a+b)(a-b)
=a2-ab+ba-b2
=a2-b2.
面积恒等
数形结合
公式应用
1.能否用公式;
2.确定a和b;
形
数
课堂小结
a2-b2.
3.正确用公式;
4.化简;
(a+b)(a-b)
=
拓展
用乘法公式计算
1.(3+2a)(3+2a)
2.(-3-2a)(-3-2a)
3.(-3+2a)(-3-2a)
4.(3-2a)(-3-2a)
1.填空:
(1)(x+ )(x - )=x2-36
(2)(m+ )(m - )=m2-25n2
(3)(a+b)( - )=b2-a2
(1)( )(1- x2)=x4-1
能力提升
2.求图中梯形的面积
能力提升
a
b
a-b
(a+b)2=a2 + 2ab + b2
(a-b)2=a2- 2ab + b2
完全平方公式:
(a +b)(a -b)=a 2-b 2
平方差公式:
两数和乘以两数差,等于这两个数的平方差.
公式对比
《课课练》
例1、例2、解答6
作业布置
9.4 乘法公式
a
a
b
b
将图中纸片只剪一刀,再拼成一个长方形.
这张纸片的面积可以表示为
a2-b2
一、新知引入
a
a
b
b
a-b
a-b
这张纸片的面积可以表示为
a2-b2
此长方形的面积还可表示为
(a+b)(a-b)
一、新知引入
这张纸片的面积可以表示为
此长方形的面积还可表示为
(a+b)(a-b)
(a+b) (a-b)=a2-b2
你有什么发现呢?
a2-b2
a
a
b
b
a-b
a-b
新知引入
你能用多项式乘法法则说明
(a +b)(a -b)=a2-b2 的正确性吗
解:(a+b)(a-b)
=a2-ab+ba-b2
=a2-b2.
公式推导
(a +b)(a -b)=a 2-b 2
平方差公式.
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
平方差公式.
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
(a +b)(a -b)=a 2-b 2
公式特征
判断:下列各式可以利用平方差公式吗?为什么?
①
②
③
④
⑤
⑥
火眼金睛
(a +b)(a -b)=a 2-b 2
例1 用平方差公式计算:
(1)
(2)
(3)
巩固练习:
1.(1+x)(1-x) 2.(a+3b)(-3b+a)
3.(-3+2a)(-3-2a) 4.(0.5x-2y)(-2y-0.5x)
典型例题
下列计算是否正确?如有错误请改正。
(1)(x+2)(x-2)=x2-2
(2)(a+b)(b- a)=a2-b2
(3)(2x+3)(2x-3)=2x2-9
(4)(x+5)(x-6)=x2-30
(5)(-1+4b)(-1-4b)=1-16b2
×
√
b2-a2
x2-4
4x2-9
巩固提高
例2 用简便方法计算:
(1)101×99; (2)
×
巩固练习 用简便方法计算:
(1)22×18;
(2)
×
典型例题
解: 101×99
=(100+1)(100-1)
=1002-12
=10000-1
=9999
1.小组内相互列举可以运用平方差公式计算的多项式乘多项式的算式;
2.小结利用公式进行计算时容易出现的问题.
小组合作
图形面积
平方差公式
感性直观
理性推导
(a+b)(a-b)
=a2-ab+ba-b2
=a2-b2.
面积恒等
数形结合
公式应用
1.能否用公式;
2.确定a和b;
形
数
课堂小结
a2-b2.
3.正确用公式;
4.化简;
(a+b)(a-b)
=
拓展
用乘法公式计算
1.(3+2a)(3+2a)
2.(-3-2a)(-3-2a)
3.(-3+2a)(-3-2a)
4.(3-2a)(-3-2a)
1.填空:
(1)(x+ )(x - )=x2-36
(2)(m+ )(m - )=m2-25n2
(3)(a+b)( - )=b2-a2
(1)( )(1- x2)=x4-1
能力提升
2.求图中梯形的面积
能力提升
a
b
a-b
(a+b)2=a2 + 2ab + b2
(a-b)2=a2- 2ab + b2
完全平方公式:
(a +b)(a -b)=a 2-b 2
平方差公式:
两数和乘以两数差,等于这两个数的平方差.
公式对比
《课课练》
例1、例2、解答6
作业布置
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
