苏科版七年级数学下册 7.4 认识三角形 课件(共15张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.4 认识三角形 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 814.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
认识三角形
将橡皮筋的一端固定在△ABC的顶点A上,另一端从点B出发沿BC方向移动,在这个过程中,橡皮筋(线段)的位置不断变化,你认为其中有哪些位置是特殊的?请与同学交流.
新课探究
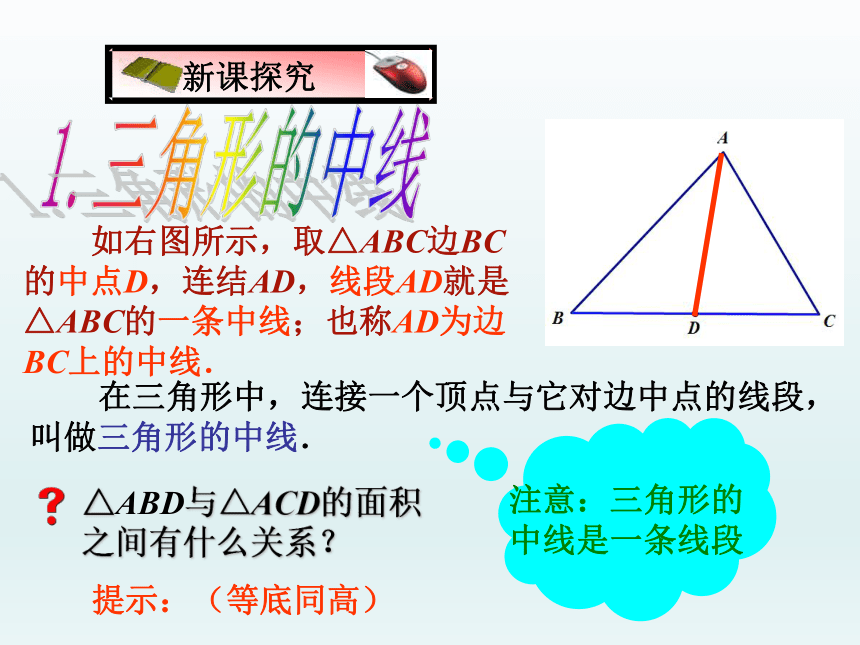
如右图所示,取△ABC边BC的中点D,连结AD,线段AD就是△ABC的一条中线;也称AD为边BC上的中线.
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线.
△ABD与△ACD的面积之间有什么关系?
注意:三角形的中线是一条线段
提示:(等底同高)
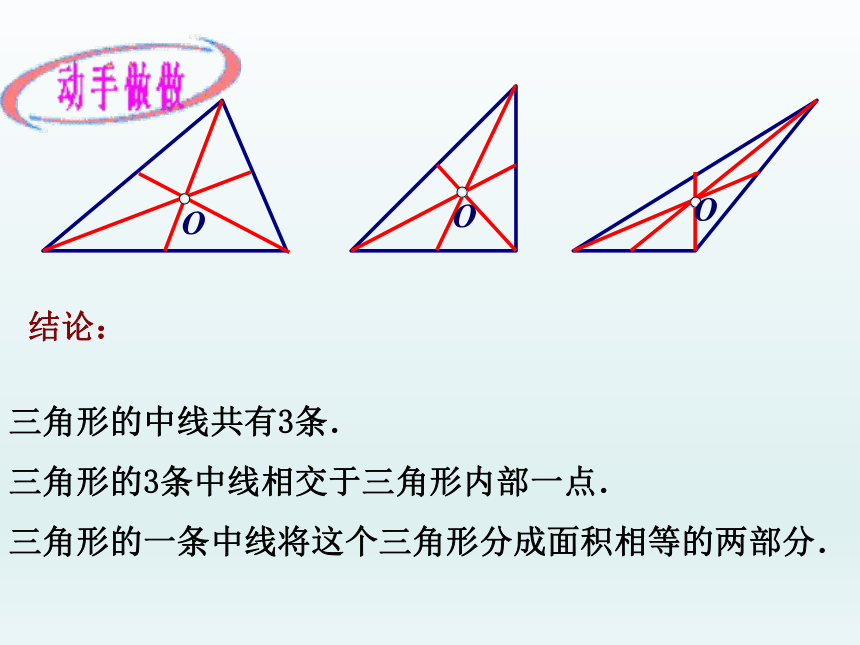
(2)观察这3条中线有什么特点?与同伴进行交流.
(1)在纸上画任意一个三角形,并画出它每条边上的中线.
议一议
三角形的中线共有3条.
三角形的3条中线相交于三角形内部一点.
三角形的一条中线将这个三角形分成面积相等的两部分.
O
O
O
结论:
新课探究
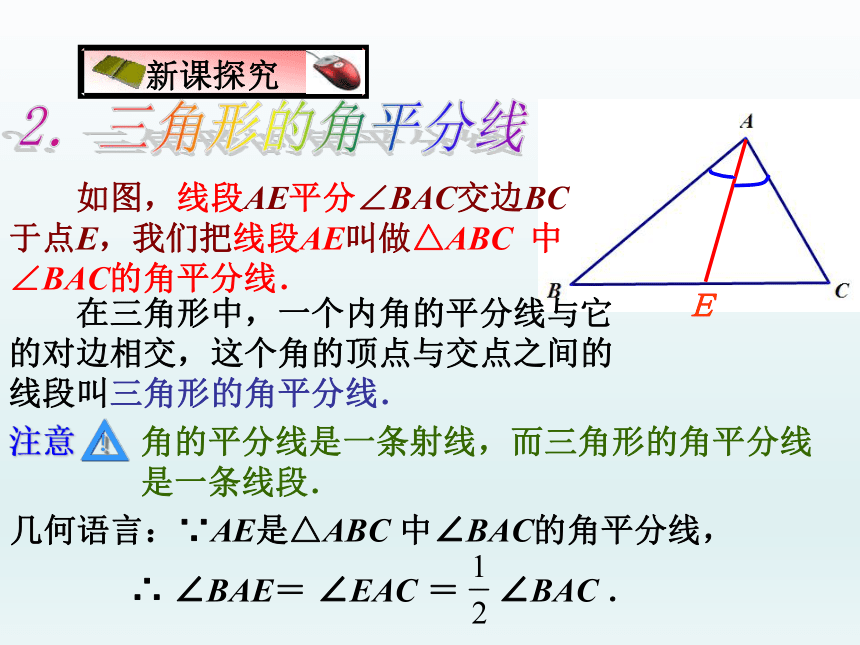
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
如图,线段AE平分∠BAC交边BC于点E,我们把线段AE叫做△ABC 中∠BAC的角平分线.
注意
!
角的平分线是一条射线,而三角形的角平分线是一条线段.
E
几何语言:∵AE是△ABC 中∠BAC的角平分线,
∴ ∠BAE= ∠EAC = ∠BAC .
议一议
(1)用折纸的方法折出三角形的三个角的平线,你有什么发现?
(2)利用量角器和直尺画出△ABC 中的角平分线.
在每个三角形中,三条角平分线之间有什么特点?将你的结果与同伴进行交流.
三角形的三条角平分线交于三角形内部一点.
三角形的角平分线共有三条.
O
O
O
结论:
新课探究
F
在三角形中,从一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
如图,线段AF垂直BC,垂足为F,我们把线段AF叫做△ABC中BC边上的高.
注意:1.三角形的高是线段,是连接三角形的顶点和相应垂足的一条线段.
2.不要忘记标上垂足和垂直符号.
三角形的3条高有交点吗?若有,交点在哪里?所在直线呢?
O
O
O
三角形的高线共有3条.锐角三角形的3条高交于
三角形内一点.
直角三角形的3条高交于直角顶点.
钝角三角形的三条高不相交,但3条高所在直线
相交于三角形外一点.
结论:
问题1:如图,在△ABC中,E是AC的中点,∠A的平分线分别交BE、BC于点F、D.指出图中哪条线段是哪个三角形的角平分线,哪条线段是哪个三角形的中线.
问题2:如图,在△ABC中,∠C=90°,点D在BC上, DE ⊥AB ,垂足为E.指出图中哪条线段是哪个三角形的高.
通过今天的学习,你知道什么是三角形的中线、角平分线和高?通过画图,你发现三角形的中线、角平分线、高各有怎样的特征?你会正确运用吗?通过这节课的学习,你能感悟“从复杂的图形中分解出简单的图形”的思考过程吗?
思考题:
如图,AF、AD分别是△ABC的高和角平分线,且∠B=36 ,∠C=66 ,求∠DAF的度数.
认识三角形
将橡皮筋的一端固定在△ABC的顶点A上,另一端从点B出发沿BC方向移动,在这个过程中,橡皮筋(线段)的位置不断变化,你认为其中有哪些位置是特殊的?请与同学交流.
新课探究
如右图所示,取△ABC边BC的中点D,连结AD,线段AD就是△ABC的一条中线;也称AD为边BC上的中线.
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线.
△ABD与△ACD的面积之间有什么关系?
注意:三角形的中线是一条线段
提示:(等底同高)
(2)观察这3条中线有什么特点?与同伴进行交流.
(1)在纸上画任意一个三角形,并画出它每条边上的中线.
议一议
三角形的中线共有3条.
三角形的3条中线相交于三角形内部一点.
三角形的一条中线将这个三角形分成面积相等的两部分.
O
O
O
结论:
新课探究
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
如图,线段AE平分∠BAC交边BC于点E,我们把线段AE叫做△ABC 中∠BAC的角平分线.
注意
!
角的平分线是一条射线,而三角形的角平分线是一条线段.
E
几何语言:∵AE是△ABC 中∠BAC的角平分线,
∴ ∠BAE= ∠EAC = ∠BAC .
议一议
(1)用折纸的方法折出三角形的三个角的平线,你有什么发现?
(2)利用量角器和直尺画出△ABC 中的角平分线.
在每个三角形中,三条角平分线之间有什么特点?将你的结果与同伴进行交流.
三角形的三条角平分线交于三角形内部一点.
三角形的角平分线共有三条.
O
O
O
结论:
新课探究
F
在三角形中,从一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
如图,线段AF垂直BC,垂足为F,我们把线段AF叫做△ABC中BC边上的高.
注意:1.三角形的高是线段,是连接三角形的顶点和相应垂足的一条线段.
2.不要忘记标上垂足和垂直符号.
三角形的3条高有交点吗?若有,交点在哪里?所在直线呢?
O
O
O
三角形的高线共有3条.锐角三角形的3条高交于
三角形内一点.
直角三角形的3条高交于直角顶点.
钝角三角形的三条高不相交,但3条高所在直线
相交于三角形外一点.
结论:
问题1:如图,在△ABC中,E是AC的中点,∠A的平分线分别交BE、BC于点F、D.指出图中哪条线段是哪个三角形的角平分线,哪条线段是哪个三角形的中线.
问题2:如图,在△ABC中,∠C=90°,点D在BC上, DE ⊥AB ,垂足为E.指出图中哪条线段是哪个三角形的高.
通过今天的学习,你知道什么是三角形的中线、角平分线和高?通过画图,你发现三角形的中线、角平分线、高各有怎样的特征?你会正确运用吗?通过这节课的学习,你能感悟“从复杂的图形中分解出简单的图形”的思考过程吗?
思考题:
如图,AF、AD分别是△ABC的高和角平分线,且∠B=36 ,∠C=66 ,求∠DAF的度数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
