2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 251.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 18:01:05 | ||
图片预览


文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
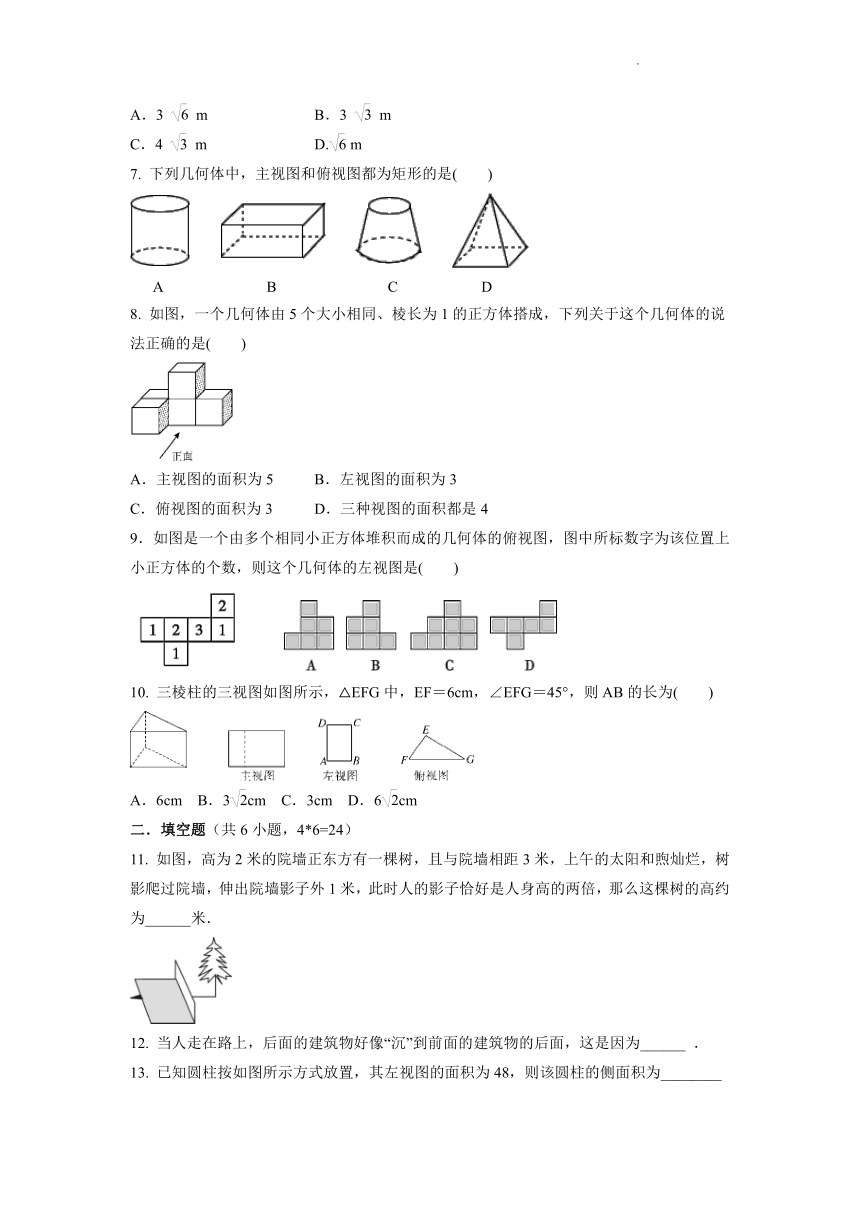
1. 下列几何体中,主视图和左视图都为矩形的是( )
2. 如图,该几何体的俯视图是( )
3. 如图是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
4. 一个几何体的三视图如图所示,则这个几何体是( )
5. 小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.上午12时 B.上午10时
C.上午9时30分 D.上午8时
6. 如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,O是“锥体”底面圆的圆心.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
A.3 m B.3 m
C.4 m D. m
7. 下列几何体中,主视图和俯视图都为矩形的是( )
A B C D
8. 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
A.主视图的面积为5 B.左视图的面积为3
C.俯视图的面积为3 D.三种视图的面积都是4
9.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所标数字为该位置上小正方体的个数,则这个几何体的左视图是( )
10. 三棱柱的三视图如图所示,△EFG中,EF=6cm,∠EFG=45°,则AB的长为( )
A.6cm B.3cm C.3cm D.6cm
二.填空题(共6小题,4*6=24)
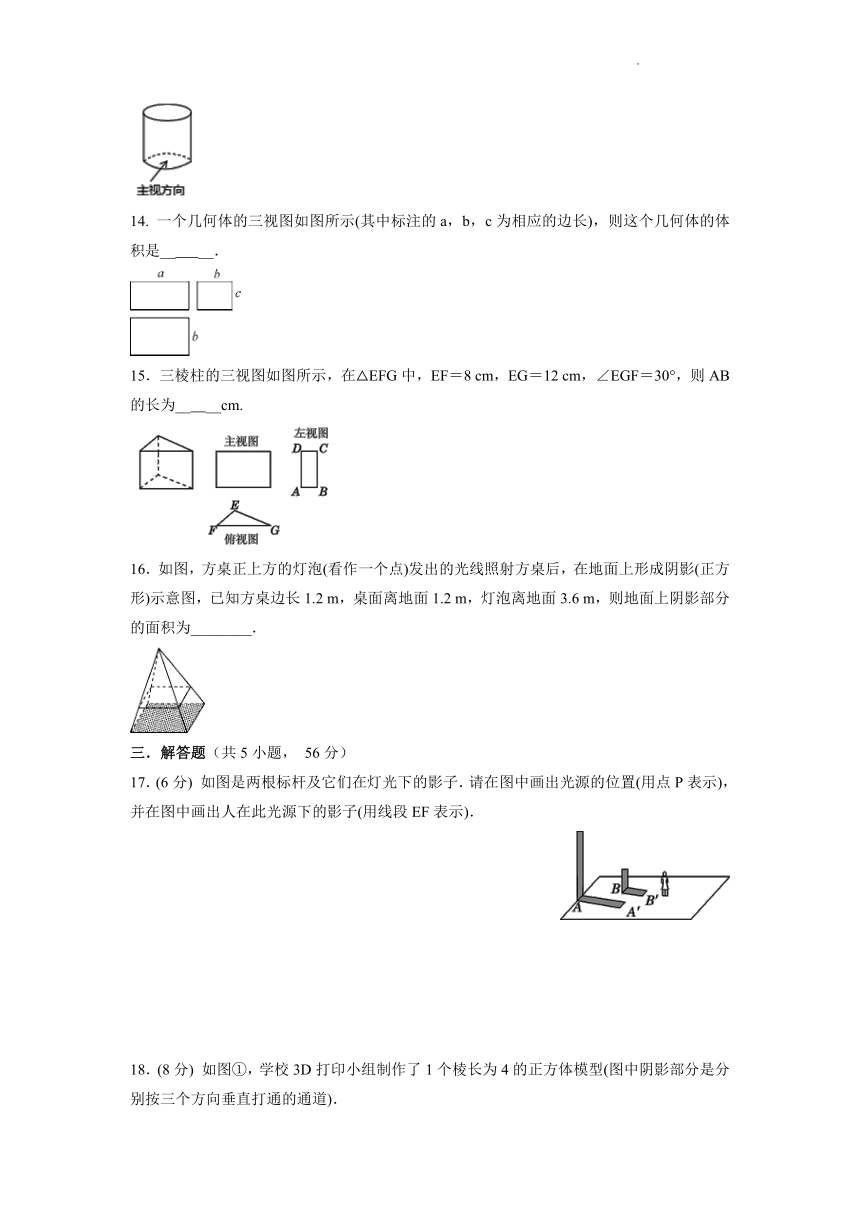
11. 如图,高为2米的院墙正东方有一棵树,且与院墙相距3米,上午的太阳和煦灿烂,树影爬过院墙,伸出院墙影子外1米,此时人的影子恰好是人身高的两倍,那么这棵树的高约为______米.
12. 当人走在路上,后面的建筑物好像“沉”到前面的建筑物的后面,这是因为______ .
13. 已知圆柱按如图所示方式放置,其左视图的面积为48,则该圆柱的侧面积为________
14. 一个几何体的三视图如图所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是__ __.
15.三棱柱的三视图如图所示,在△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为__ __cm.
16.如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为________.
三.解答题(共5小题, 56分)
17.(6分) 如图是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子(用线段EF表示).
18.(8分) 如图①,学校3D打印小组制作了1个棱长为4的正方体模型(图中阴影部分是分别按三个方向垂直打通的通道).
(1)按从前往后的顺序,在图②中,依次画出每一层从正面看到的图形,通道部分用阴影表示;
(2)求这个正方体模型的体积.
19.(8分) 如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为多少?
20.(10分) 小明的身高如图中线段AB所示,在路灯下,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子;
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.
21.(12分) 如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
22.(12分) 如图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形.现将宽为15 cm的彩色矩形纸带AMCN沿虚线裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算∠BAD的度数;
(2)计算按图③的方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
参考答案
1-5BACDD 6-10ABBBB
11.4
12. 到了自己的盲区的范围内
13.48π
14.abc
15.6
16.3.24 m2
17.解:如图,点P是光源,EF就是人在光源P下的影子.
18.解:(1)如图所示.
(2)(13+11+11+13)×(1×1×1)=48.故这个正方体模型的体积是48.
19.如图所示,∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12cm,QA=5cm,∴PQ==13cm.
20. 解:(1)如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)由已知可得=,∴=,∴OD=4 m.答:灯泡的高为4 m.
21. 解:由题意可知OD=OE,∠DOE=90°,∴∠DEO=45°.又∵∠ABE=90°,∴∠BAE=45°=∠DEO.∴AB=BE,即AB=BO+OE.连接CD,易知C,D,O三点在同一直线上.在△ABF和△COF中,∠ABF=∠COF=90°,∠AFB=∠CFO,∴△ABF∽△COF.∴=,∴=,即=,即=.∴BO=3.6 (m).∴AB=3.6+0.8=4.4(m),即围墙AB的高度为4.4 m.
22. 解:(1)AB的长等于三棱柱的底面周长,为30 cm.∵纸带的宽为15 cm,∴sin∠BAD=sin∠ABM===,∴∠DAB=30°.
(2)在题图中,将三棱柱沿过点A的侧棱剪开,得到如图所示的侧面展开图.将△ABE向左平移30 cm,△CDF向右平移30 cm,拼成如图所示的平行四边形A′B′C′D′.此平行四边形即为题图②中的平行四边形ABCD.易得AC′=2AE=2×=40(cm),∴在题图②中,BC=40cm,∴所需矩形纸带的长度为MB+BC=30·cos 30°+40=55(cm).
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列几何体中,主视图和左视图都为矩形的是( )
2. 如图,该几何体的俯视图是( )
3. 如图是由两个相同的小正方体和一个圆锥体组成的立体图形,其俯视图是( )
4. 一个几何体的三视图如图所示,则这个几何体是( )
5. 小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.上午12时 B.上午10时
C.上午9时30分 D.上午8时
6. 如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,O是“锥体”底面圆的圆心.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
A.3 m B.3 m
C.4 m D. m
7. 下列几何体中,主视图和俯视图都为矩形的是( )
A B C D
8. 如图,一个几何体由5个大小相同、棱长为1的正方体搭成,下列关于这个几何体的说法正确的是( )
A.主视图的面积为5 B.左视图的面积为3
C.俯视图的面积为3 D.三种视图的面积都是4
9.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所标数字为该位置上小正方体的个数,则这个几何体的左视图是( )
10. 三棱柱的三视图如图所示,△EFG中,EF=6cm,∠EFG=45°,则AB的长为( )
A.6cm B.3cm C.3cm D.6cm
二.填空题(共6小题,4*6=24)
11. 如图,高为2米的院墙正东方有一棵树,且与院墙相距3米,上午的太阳和煦灿烂,树影爬过院墙,伸出院墙影子外1米,此时人的影子恰好是人身高的两倍,那么这棵树的高约为______米.
12. 当人走在路上,后面的建筑物好像“沉”到前面的建筑物的后面,这是因为______ .
13. 已知圆柱按如图所示方式放置,其左视图的面积为48,则该圆柱的侧面积为________
14. 一个几何体的三视图如图所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是__ __.
15.三棱柱的三视图如图所示,在△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为__ __cm.
16.如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为________.
三.解答题(共5小题, 56分)
17.(6分) 如图是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子(用线段EF表示).
18.(8分) 如图①,学校3D打印小组制作了1个棱长为4的正方体模型(图中阴影部分是分别按三个方向垂直打通的通道).
(1)按从前往后的顺序,在图②中,依次画出每一层从正面看到的图形,通道部分用阴影表示;
(2)求这个正方体模型的体积.
19.(8分) 如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为多少?
20.(10分) 小明的身高如图中线段AB所示,在路灯下,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子;
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.
21.(12分) 如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
22.(12分) 如图①是一个三棱柱包装盒,它的底面是边长为10 cm的正三角形,三个侧面都是矩形.现将宽为15 cm的彩色矩形纸带AMCN沿虚线裁剪成一个平行四边形ABCD(如图②),然后用这条平行四边形纸带按如图③的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图②中,计算∠BAD的度数;
(2)计算按图③的方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
参考答案
1-5BACDD 6-10ABBBB
11.4
12. 到了自己的盲区的范围内
13.48π
14.abc
15.6
16.3.24 m2
17.解:如图,点P是光源,EF就是人在光源P下的影子.
18.解:(1)如图所示.
(2)(13+11+11+13)×(1×1×1)=48.故这个正方体模型的体积是48.
19.如图所示,∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12cm,QA=5cm,∴PQ==13cm.
20. 解:(1)如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)由已知可得=,∴=,∴OD=4 m.答:灯泡的高为4 m.
21. 解:由题意可知OD=OE,∠DOE=90°,∴∠DEO=45°.又∵∠ABE=90°,∴∠BAE=45°=∠DEO.∴AB=BE,即AB=BO+OE.连接CD,易知C,D,O三点在同一直线上.在△ABF和△COF中,∠ABF=∠COF=90°,∠AFB=∠CFO,∴△ABF∽△COF.∴=,∴=,即=,即=.∴BO=3.6 (m).∴AB=3.6+0.8=4.4(m),即围墙AB的高度为4.4 m.
22. 解:(1)AB的长等于三棱柱的底面周长,为30 cm.∵纸带的宽为15 cm,∴sin∠BAD=sin∠ABM===,∴∠DAB=30°.
(2)在题图中,将三棱柱沿过点A的侧棱剪开,得到如图所示的侧面展开图.将△ABE向左平移30 cm,△CDF向右平移30 cm,拼成如图所示的平行四边形A′B′C′D′.此平行四边形即为题图②中的平行四边形ABCD.易得AC′=2AE=2×=40(cm),∴在题图②中,BC=40cm,∴所需矩形纸带的长度为MB+BC=30·cos 30°+40=55(cm).
