2021-2022学年北师大版八年级数学下册《第一章三角形的证明》阶段过关专练(考查范围:1.1等腰三角形、1.2直角三角形)同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册《第一章三角形的证明》阶段过关专练(考查范围:1.1等腰三角形、1.2直角三角形)同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 19:45:24 | ||
图片预览




文档简介
北师大版八年级下册数学《三角形的证明》阶段过关专练
(考查范围:1.1等腰三角形、1.2直角三角形)
基础巩固专题
一、选择题。
1. 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为 ( )
A.48° B.40° C.30° D.24°
2. 若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为 ( )
A.2 cm B.4 cm C.6 cm D.8 cm
3. △ABC的三边长分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件不能判定△ABC是直角三角形的是 ( )
A.∠B=∠A-∠C B.a∶b∶c=5∶12∶13
C.b2-a2=c2 D.∠A∶∠B∶∠C=3∶4∶5
4. 如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则无法得出的结论是( )
A.OA=OB B.E是AC的中点
C.△AOE≌△BOD D.AE=BD
5. 如图,点D,E分别在等边三角形ABC的边BC,AC上,且BD=CE,连接AD,BE相交于点P,则∠APE的度数是 ( )
A.60° B.55° C.45° D.30°
二、填空题。
6. 已知AB=20,AC=30,∠A=150°,则△ABC的面积是_____.
7. 我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k= ,则该等腰三角形的顶角为 度.
8. 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3 cm,则AB= cm.
9. 已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 .
三、解答题。
10. 如图,已知∠BAC=60°,D是BC边上一点,AD=CD,∠ADB=80°,求∠B的度数.
11. 已知:如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
12. 张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
能力提升专题
一、选择题。
1. 如图,长方形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有 ( )
A.3对 B.4对 C.5对 D.6对
2. 如果等腰三角形的一个角等于42°,则它的底角是 ( )
A.42° B.69°
C.49°或84° D.42°或69°
3.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是 ( )
A. B. C. D.
4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. 9 B.6 C. 4 D.3
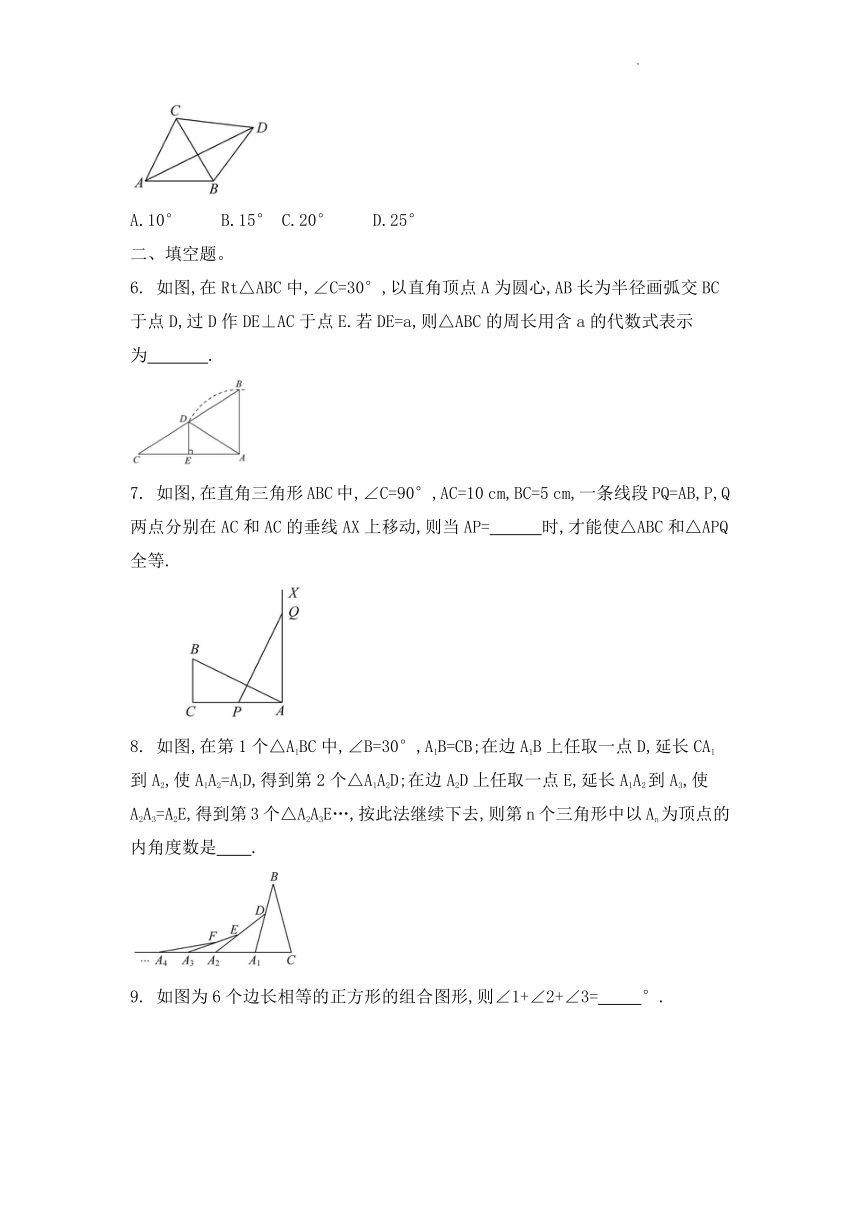
5.如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为
( )
A.10° B.15° C.20° D.25°
二、填空题。
6. 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
7. 如图,在直角三角形ABC中,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP= 时,才能使△ABC和△APQ全等.
8. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E…,按此法继续下去,则第n个三角形中以An为顶点的内角度数是 .
9. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= °.
三、解答题。
10. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB. (7分)
11. 如图,A,B,C三点在同一直线上,分别以AB,BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.
(1)求证:△ABE≌△DBC.
(2)试判断△BMN的形状,并说明理由.
12. 已知,如图在△ABC中,BC=6,AC=8,DE是AB边上的高,DE=7,△ABE的面积为35.
(1)求AB的长.
(2)求四边形ACBE的面积.
北师大版八年级下册数学《三角形的证明》阶段过关专练
(考查范围:1.1等腰三角形、1.2直角三角形)(答案版)
基础巩固专题
一、选择题。
1. 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为 ( D )
A.48° B.40° C.30° D.24°
2. 若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为 ( A )
A.2 cm B.4 cm C.6 cm D.8 cm
3. △ABC的三边长分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件不能判定△ABC是直角三角形的是 ( D )
A.∠B=∠A-∠C B.a∶b∶c=5∶12∶13
C.b2-a2=c2 D.∠A∶∠B∶∠C=3∶4∶5
4. 如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则无法得出的结论是( B )
A.OA=OB B.E是AC的中点
C.△AOE≌△BOD D.AE=BD
5. 如图,点D,E分别在等边三角形ABC的边BC,AC上,且BD=CE,连接AD,BE相交于点P,则∠APE的度数是 ( A )
A.60° B.55° C.45° D.30°
二、填空题。
6. 已知AB=20,AC=30,∠A=150°,则△ABC的面积是__150___.
7. 我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k= ,则该等腰三角形的顶角为 36 度.
8. 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3 cm,则AB= 6 cm.
9. 已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 2或2 .
三、解答题。
10. 如图,已知∠BAC=60°,D是BC边上一点,AD=CD,∠ADB=80°,求∠B的度数.
解:∵∠ADB=80°,
又∵AD=CD,
∴∠DAC=∠C=40°,
∴∠B=180°-∠BAC-∠C
=180°-60°-40°=80°.
11. 已知:如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
解:△CEB是等边三角形.
理由如下:∵AB=BC,∠ABC=120°,BE⊥AC,
∴∠CBE=∠ABE=60°.
又DE=DB,BE⊥AC,
∴CB=CE,∴△CEB是等边三角形.
12. 张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
解:(1)当∠A为顶角时,∠B=50°,
当∠A为底角时,若∠B为顶角,
则∠B=20°,
若∠B为底角,则∠B=80°,
∴∠B=50°或20°或80°.
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个.
②当0若∠A为顶角,则∠B=°,若∠A为底角时,则∠B=x°或∠B=(180-2x)°,
当≠180-2x且≠x且180-2x≠x,即当x≠60时,∠B有三个不同的度数.
综上①②,当0∠B有三个不同的度数.
能力提升专题
一、选择题。
1. 如图,长方形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有 ( B )
A.3对 B.4对 C.5对 D.6对
2. 如果等腰三角形的一个角等于42°,则它的底角是 ( D )
A.42° B.69°
C.49°或84° D.42°或69°
3.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是 ( B )
A. B. C. D.
4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( D )
A. 9 B.6 C. 4 D.3
5.如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为
( C )
A.10° B.15° C.20° D.25°
二、填空题。
6. 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 (6+2)a .
7. 如图,在直角三角形ABC中,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP= 5 cm或10 cm 时,才能使△ABC和△APQ全等.
8. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=
A2E,得到第3个△A2A3E…,按此法继续下去,则第n个三角形中以An为顶点的内角度数是 ×75° .
9. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= 135 °.
三、解答题。
10. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB. (7分)
证明:∵AD⊥DE,BE⊥DE,∠ACB=90°,
∴∠ADC=∠ACB=∠BEC=90°,
∴∠DAC+∠DCA=90°,
∠DCA+∠ECB=180°-90°=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS)
11. 如图,A,B,C三点在同一直线上,分别以AB,BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.
(1)求证:△ABE≌△DBC.
(2)试判断△BMN的形状,并说明理由.
解:(1)证明:∵等边△ABD和等边△BCE,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
在△ABE和△DBC中,
∵,
∴△ABE≌△DBC(SAS).
(2)△BMN为等边三角形,理由为:
证明:∵△ABE≌△DBC,
∴∠AEB=∠DCB,
又∠ABD=∠EBC=60°,
∴∠MBE=180°-60°-60°=60°,
即∠MBE=∠NBC=60°,
在△MBE和△NBC中,
∵
∴△MBE≌△NBC(ASA),
∴BM=BN,∠MBE=60°,
则△BMN为等边三角形.
12. 已知,如图在△ABC中,BC=6,AC=8,DE是AB边上的高,DE=7,△ABE的面积为35.
(1)求AB的长.
(2)求四边形ACBE的面积.
解:(1)∵在△ABE中,DE是AB边上的高,DE=7,△ABE的面积为35,
∴S△ABE=AB×DE=AB×7=35,
∴AB=10.
(2)∵在△ABC中,BC=6,AC=8,AB=10,
∴AC2+BC2=82+62=100,AB2=102=100,
∴AC2+BC2=AB2,∴△ABC是直角三角形,
∴S△ABC=×6×8=24,∴四边形ACBE的面积=S△ABC+S△ABE=24+35=59.
(考查范围:1.1等腰三角形、1.2直角三角形)
基础巩固专题
一、选择题。
1. 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为 ( )
A.48° B.40° C.30° D.24°
2. 若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为 ( )
A.2 cm B.4 cm C.6 cm D.8 cm
3. △ABC的三边长分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件不能判定△ABC是直角三角形的是 ( )
A.∠B=∠A-∠C B.a∶b∶c=5∶12∶13
C.b2-a2=c2 D.∠A∶∠B∶∠C=3∶4∶5
4. 如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则无法得出的结论是( )
A.OA=OB B.E是AC的中点
C.△AOE≌△BOD D.AE=BD
5. 如图,点D,E分别在等边三角形ABC的边BC,AC上,且BD=CE,连接AD,BE相交于点P,则∠APE的度数是 ( )
A.60° B.55° C.45° D.30°
二、填空题。
6. 已知AB=20,AC=30,∠A=150°,则△ABC的面积是_____.
7. 我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k= ,则该等腰三角形的顶角为 度.
8. 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3 cm,则AB= cm.
9. 已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 .
三、解答题。
10. 如图,已知∠BAC=60°,D是BC边上一点,AD=CD,∠ADB=80°,求∠B的度数.
11. 已知:如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
12. 张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
能力提升专题
一、选择题。
1. 如图,长方形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有 ( )
A.3对 B.4对 C.5对 D.6对
2. 如果等腰三角形的一个角等于42°,则它的底角是 ( )
A.42° B.69°
C.49°或84° D.42°或69°
3.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是 ( )
A. B. C. D.
4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. 9 B.6 C. 4 D.3
5.如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为
( )
A.10° B.15° C.20° D.25°
二、填空题。
6. 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
7. 如图,在直角三角形ABC中,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP= 时,才能使△ABC和△APQ全等.
8. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E…,按此法继续下去,则第n个三角形中以An为顶点的内角度数是 .
9. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= °.
三、解答题。
10. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB. (7分)
11. 如图,A,B,C三点在同一直线上,分别以AB,BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.
(1)求证:△ABE≌△DBC.
(2)试判断△BMN的形状,并说明理由.
12. 已知,如图在△ABC中,BC=6,AC=8,DE是AB边上的高,DE=7,△ABE的面积为35.
(1)求AB的长.
(2)求四边形ACBE的面积.
北师大版八年级下册数学《三角形的证明》阶段过关专练
(考查范围:1.1等腰三角形、1.2直角三角形)(答案版)
基础巩固专题
一、选择题。
1. 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为 ( D )
A.48° B.40° C.30° D.24°
2. 若等腰三角形的周长为10 cm,其中一边长为2 cm,则该等腰三角形的底边长为 ( A )
A.2 cm B.4 cm C.6 cm D.8 cm
3. △ABC的三边长分别为a,b,c,其对角分别为∠A,∠B,∠C.下列条件不能判定△ABC是直角三角形的是 ( D )
A.∠B=∠A-∠C B.a∶b∶c=5∶12∶13
C.b2-a2=c2 D.∠A∶∠B∶∠C=3∶4∶5
4. 如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则无法得出的结论是( B )
A.OA=OB B.E是AC的中点
C.△AOE≌△BOD D.AE=BD
5. 如图,点D,E分别在等边三角形ABC的边BC,AC上,且BD=CE,连接AD,BE相交于点P,则∠APE的度数是 ( A )
A.60° B.55° C.45° D.30°
二、填空题。
6. 已知AB=20,AC=30,∠A=150°,则△ABC的面积是__150___.
7. 我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k= ,则该等腰三角形的顶角为 36 度.
8. 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3 cm,则AB= 6 cm.
9. 已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为 2或2 .
三、解答题。
10. 如图,已知∠BAC=60°,D是BC边上一点,AD=CD,∠ADB=80°,求∠B的度数.
解:∵∠ADB=80°,
又∵AD=CD,
∴∠DAC=∠C=40°,
∴∠B=180°-∠BAC-∠C
=180°-60°-40°=80°.
11. 已知:如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
解:△CEB是等边三角形.
理由如下:∵AB=BC,∠ABC=120°,BE⊥AC,
∴∠CBE=∠ABE=60°.
又DE=DB,BE⊥AC,
∴CB=CE,∴△CEB是等边三角形.
12. 张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
解:(1)当∠A为顶角时,∠B=50°,
当∠A为底角时,若∠B为顶角,
则∠B=20°,
若∠B为底角,则∠B=80°,
∴∠B=50°或20°或80°.
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个.
②当0
当≠180-2x且≠x且180-2x≠x,即当x≠60时,∠B有三个不同的度数.
综上①②,当0
能力提升专题
一、选择题。
1. 如图,长方形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD,DF,则图中全等的直角三角形共有 ( B )
A.3对 B.4对 C.5对 D.6对
2. 如果等腰三角形的一个角等于42°,则它的底角是 ( D )
A.42° B.69°
C.49°或84° D.42°或69°
3.如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是 ( B )
A. B. C. D.
4.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( D )
A. 9 B.6 C. 4 D.3
5.如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为
( C )
A.10° B.15° C.20° D.25°
二、填空题。
6. 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 (6+2)a .
7. 如图,在直角三角形ABC中,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP= 5 cm或10 cm 时,才能使△ABC和△APQ全等.
8. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=
A2E,得到第3个△A2A3E…,按此法继续下去,则第n个三角形中以An为顶点的内角度数是 ×75° .
9. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= 135 °.
三、解答题。
10. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.
求证:△ADC≌△CEB. (7分)
证明:∵AD⊥DE,BE⊥DE,∠ACB=90°,
∴∠ADC=∠ACB=∠BEC=90°,
∴∠DAC+∠DCA=90°,
∠DCA+∠ECB=180°-90°=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS)
11. 如图,A,B,C三点在同一直线上,分别以AB,BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.
(1)求证:△ABE≌△DBC.
(2)试判断△BMN的形状,并说明理由.
解:(1)证明:∵等边△ABD和等边△BCE,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
在△ABE和△DBC中,
∵,
∴△ABE≌△DBC(SAS).
(2)△BMN为等边三角形,理由为:
证明:∵△ABE≌△DBC,
∴∠AEB=∠DCB,
又∠ABD=∠EBC=60°,
∴∠MBE=180°-60°-60°=60°,
即∠MBE=∠NBC=60°,
在△MBE和△NBC中,
∵
∴△MBE≌△NBC(ASA),
∴BM=BN,∠MBE=60°,
则△BMN为等边三角形.
12. 已知,如图在△ABC中,BC=6,AC=8,DE是AB边上的高,DE=7,△ABE的面积为35.
(1)求AB的长.
(2)求四边形ACBE的面积.
解:(1)∵在△ABE中,DE是AB边上的高,DE=7,△ABE的面积为35,
∴S△ABE=AB×DE=AB×7=35,
∴AB=10.
(2)∵在△ABC中,BC=6,AC=8,AB=10,
∴AC2+BC2=82+62=100,AB2=102=100,
∴AC2+BC2=AB2,∴△ABC是直角三角形,
∴S△ABC=×6×8=24,∴四边形ACBE的面积=S△ABC+S△ABE=24+35=59.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
