2021-2022学年北师大版八年级数学下册2.1不等关系培优训练(Word版 含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册2.1不等关系培优训练(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 78.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 19:43:50 | ||
图片预览


文档简介
一元一次不等式与一元一次不等式
《不等关系》同步培优训练
选择。
1.下面给出的5个式子:①3>0;②4x+y<2;③2x=3;④ x-1;⑤x-2≥3.其中不等式有( )
A.2个 B.3个 C.4个 D.5个
2.铺设木地板时,每两块地板之间的缝隙不低于0.5mm且不超过0.8mm,缝隙的宽度可以是( )
A.0.3mm B.0.4mm C.0.6mm D.0.9mm
3.下列不等关系中正确的是( )
A.a不是负数表示为a>0 B.x不大于8表示为x>8
C.x与2的和是非负数表示为x+2>0 D.m与4的差是负数表示为m—4<0
4.下列各项中,蕴含不等关系的是( )
A.老师的年龄是小明的年龄的3倍 B.小明和小亮一样高
C.小明的岁数比爸爸小26岁 D.x2是非负数
5.学校组织同学们春游,租用45座和30座两种型号的客车,若租用45座客车x辆,租用30座客车y辆,则不等式“45x+30y≥500”表示的实际意义是( )
A.两种客车总的载客量不少于500人
B.两种客车总的载客量不超过500人
C.两种客车总的载客量不足500人
D.两种客车总的载客量恰好等于500人
6.某种品牌的八宝粥,外包装标明:净含量为330±10g,表明了这罐八宝粥的净含量x的范围是( )
A. B.
C. D.
7.学校组织同学们春游,租用45座和30座两种型号的客车,若租用45座客车x辆,租用30座客车y辆,则不等式“45x+30y≥500”表示的实际意义是( )
A.两种客车总的载客量不少于500人
B.两种客车总的载客量不超过500人
C.两种客车总的载客量不足500人
D.两种客车总的载客量恰好等于500人
8.下面列出的不等式中,正确的是( )
A.“m不是正数”表示为m<0
B.“m不大于3”表示为m<3
C.“n与4的差是负数”表示为n﹣4<0
D.“n不等于6”表示为n>6
9.关于下列问题的解答,错误的是( )
A.x的3倍不小于y的,可表示为3x>y
B.m的与n的和是非负数,可表示为+n≥0
C.a是非负数,可表示为a≥0
D.是负数,可表示为<0
10.某食品外包装标明“净含量为(350±10)克”,表明这种食品的净含量x(克)的范围是( )
A. B.
C. D.
二、填空。
11.根据“a的3倍与2的差小于0”列出的不等式是:_____.
12.一种饮料重约300克,罐上注有“蛋白质含量≥0.5%”,其中蛋白质的含量最少为 克.
13.数学表达式中:①a2≥0 ②5p﹣6q<0 ③x﹣6=1 ④7x+8y⑤﹣1<0 ⑥x≠3不等式是 (填序号).
14.填写等于或不等号.
(1)5 3.
(2)﹣5×0 0×3.
(3)a2 0.
(4)﹣x2﹣1 0.
15.2020年2月5日某市气象台预报该市气温是﹣2~5℃,这表示2月5日该市的最低气温是 ℃,最高气温是 ℃.设该市2月5日某一时刻气温为t℃,则关于t的不等关系是 .
三、解答。
16.用适当的不等式表示下列不等关系:
(1)x的与x的2倍的和是非负数;
(2)一枚炮弹的杀伤力半径不小于300米;
(3)三件上衣和四条裤子的总价钱不高于368元;
(4)明天下雨的可能性不小于70%;
(5)小明的体重不比小亮的轻;
17.用适当的符号表示下列关系:
(1)一枚炮弹的杀伤半径不小于300米;
(2)三件上衣与四条长裤的总价钱不高于268元;
(3)明天下雨的可能性不小于70%;
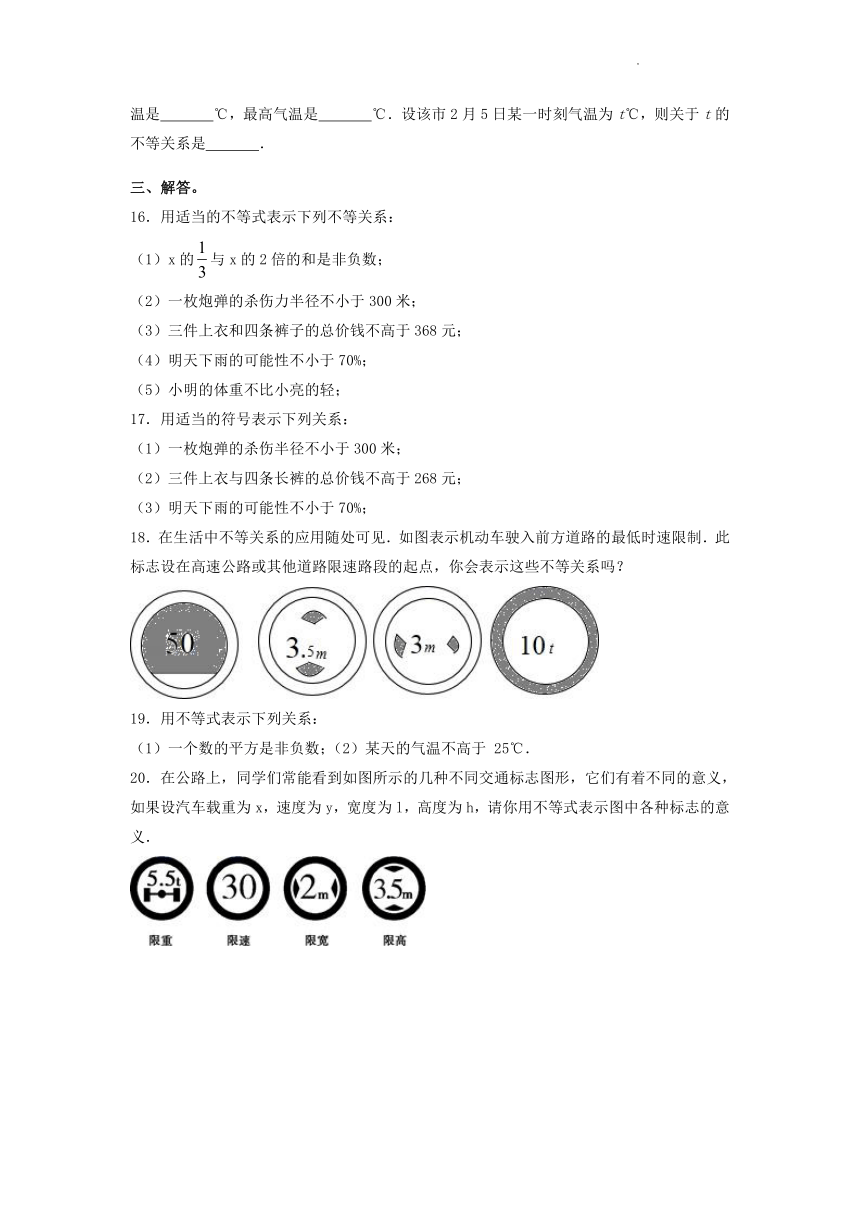
18.在生活中不等关系的应用随处可见.如图表示机动车驶入前方道路的最低时速限制.此标志设在高速公路或其他道路限速路段的起点,你会表示这些不等关系吗?
19.用不等式表示下列关系:
(1)一个数的平方是非负数;(2)某天的气温不高于 25℃.
20.在公路上,同学们常能看到如图所示的几种不同交通标志图形,它们有着不同的意义,如果设汽车载重为x,速度为y,宽度为l,高度为h,请你用不等式表示图中各种标志的意义.
答案
1-5:BCDDA 6-10:DACAD
12.解:∵某种饮料重约300g,罐上注有“蛋白质含量≥0.5%”,
∴蛋白质含量的最小值=300×0.5%=1.5克,
∴白质的含量不少于1.5克.
故答案是:1.5.
13.解:在①a2≥0 ②5p﹣6q<0 ③x﹣6=1 ④7x+8y⑤﹣1<0 ⑥x≠3中,除③x﹣6=1、④7x+8y之外,式子都含不等号,是不等式,共4个,为①②⑤⑥.
14.解:1)5>3,
(2)﹣5×0=0×3,
(3)a2≥0,
(4)﹣x2﹣1≤0,
故答案为:>,=,≥,≤.
15.解:2012年2月5日某市气象台预报该市气温是﹣2~5℃,这表示2月5日该市的最低气温是﹣2℃,最高气温是 5℃.设该市2月5日某一时刻气温为t℃,则关于t的不等关系是﹣2≤t≤5.
故答案为:﹣2,5,﹣2≤t≤5.
16.(1)x+2x≥0;
(2)设炮弹的杀伤半径为r,则应有r≥300;
(3)设每件上衣为a元,每条长裤是b元,应有3a+4b≤368;
(4)用P表示明天下雨的可能性,则有P≥70%;
(5)设小明的体重为a千克,小亮的体重为b千克,则应有a≥b.
17.解:(1)﹣π<﹣3;
(2)a2≥0;
(3)∵x,y的值不确定∴|x|+|y|≥|x+y|;
(4)(﹣5)÷(﹣1)=5>(﹣6)÷(﹣7)=;
(5)当a≤0时,|a|=﹣a.
18.解:由数轴可得m<n<0,
(1)两个负数相加,和仍为负数,故m+n<0;
(2)相当于两个异号的数相加,符号由绝对值大的数决定,故m﹣n<0;
(3)两个负数的积是正数,故m n>0;
(4)正数大于一切负数,故m2>n;
(5)由数轴离原点的距离可得,|m|>|n|.
19.解:(1)x+2x≤0;
(2)设炮弹的杀伤半径为r,则应有r≥300;
(3)设每件上衣为a元,每条长裤是b元,应有3a+4b≤268;
(4)用P表示明天下雨的可能性,则有P≥70%;
(5)设小明的体重为a千克,小刚的体重为b千克,则应有a≥b.
20.由题意可知,限重、限宽、限高、限速中的“限”字的意义就是不超过,也就是“≤”的意义,即:x≤5.5t,y≤30km/h,l≤2m,h≤3.5m.
《不等关系》同步培优训练
选择。
1.下面给出的5个式子:①3>0;②4x+y<2;③2x=3;④ x-1;⑤x-2≥3.其中不等式有( )
A.2个 B.3个 C.4个 D.5个
2.铺设木地板时,每两块地板之间的缝隙不低于0.5mm且不超过0.8mm,缝隙的宽度可以是( )
A.0.3mm B.0.4mm C.0.6mm D.0.9mm
3.下列不等关系中正确的是( )
A.a不是负数表示为a>0 B.x不大于8表示为x>8
C.x与2的和是非负数表示为x+2>0 D.m与4的差是负数表示为m—4<0
4.下列各项中,蕴含不等关系的是( )
A.老师的年龄是小明的年龄的3倍 B.小明和小亮一样高
C.小明的岁数比爸爸小26岁 D.x2是非负数
5.学校组织同学们春游,租用45座和30座两种型号的客车,若租用45座客车x辆,租用30座客车y辆,则不等式“45x+30y≥500”表示的实际意义是( )
A.两种客车总的载客量不少于500人
B.两种客车总的载客量不超过500人
C.两种客车总的载客量不足500人
D.两种客车总的载客量恰好等于500人
6.某种品牌的八宝粥,外包装标明:净含量为330±10g,表明了这罐八宝粥的净含量x的范围是( )
A. B.
C. D.
7.学校组织同学们春游,租用45座和30座两种型号的客车,若租用45座客车x辆,租用30座客车y辆,则不等式“45x+30y≥500”表示的实际意义是( )
A.两种客车总的载客量不少于500人
B.两种客车总的载客量不超过500人
C.两种客车总的载客量不足500人
D.两种客车总的载客量恰好等于500人
8.下面列出的不等式中,正确的是( )
A.“m不是正数”表示为m<0
B.“m不大于3”表示为m<3
C.“n与4的差是负数”表示为n﹣4<0
D.“n不等于6”表示为n>6
9.关于下列问题的解答,错误的是( )
A.x的3倍不小于y的,可表示为3x>y
B.m的与n的和是非负数,可表示为+n≥0
C.a是非负数,可表示为a≥0
D.是负数,可表示为<0
10.某食品外包装标明“净含量为(350±10)克”,表明这种食品的净含量x(克)的范围是( )
A. B.
C. D.
二、填空。
11.根据“a的3倍与2的差小于0”列出的不等式是:_____.
12.一种饮料重约300克,罐上注有“蛋白质含量≥0.5%”,其中蛋白质的含量最少为 克.
13.数学表达式中:①a2≥0 ②5p﹣6q<0 ③x﹣6=1 ④7x+8y⑤﹣1<0 ⑥x≠3不等式是 (填序号).
14.填写等于或不等号.
(1)5 3.
(2)﹣5×0 0×3.
(3)a2 0.
(4)﹣x2﹣1 0.
15.2020年2月5日某市气象台预报该市气温是﹣2~5℃,这表示2月5日该市的最低气温是 ℃,最高气温是 ℃.设该市2月5日某一时刻气温为t℃,则关于t的不等关系是 .
三、解答。
16.用适当的不等式表示下列不等关系:
(1)x的与x的2倍的和是非负数;
(2)一枚炮弹的杀伤力半径不小于300米;
(3)三件上衣和四条裤子的总价钱不高于368元;
(4)明天下雨的可能性不小于70%;
(5)小明的体重不比小亮的轻;
17.用适当的符号表示下列关系:
(1)一枚炮弹的杀伤半径不小于300米;
(2)三件上衣与四条长裤的总价钱不高于268元;
(3)明天下雨的可能性不小于70%;
18.在生活中不等关系的应用随处可见.如图表示机动车驶入前方道路的最低时速限制.此标志设在高速公路或其他道路限速路段的起点,你会表示这些不等关系吗?
19.用不等式表示下列关系:
(1)一个数的平方是非负数;(2)某天的气温不高于 25℃.
20.在公路上,同学们常能看到如图所示的几种不同交通标志图形,它们有着不同的意义,如果设汽车载重为x,速度为y,宽度为l,高度为h,请你用不等式表示图中各种标志的意义.
答案
1-5:BCDDA 6-10:DACAD
12.解:∵某种饮料重约300g,罐上注有“蛋白质含量≥0.5%”,
∴蛋白质含量的最小值=300×0.5%=1.5克,
∴白质的含量不少于1.5克.
故答案是:1.5.
13.解:在①a2≥0 ②5p﹣6q<0 ③x﹣6=1 ④7x+8y⑤﹣1<0 ⑥x≠3中,除③x﹣6=1、④7x+8y之外,式子都含不等号,是不等式,共4个,为①②⑤⑥.
14.解:1)5>3,
(2)﹣5×0=0×3,
(3)a2≥0,
(4)﹣x2﹣1≤0,
故答案为:>,=,≥,≤.
15.解:2012年2月5日某市气象台预报该市气温是﹣2~5℃,这表示2月5日该市的最低气温是﹣2℃,最高气温是 5℃.设该市2月5日某一时刻气温为t℃,则关于t的不等关系是﹣2≤t≤5.
故答案为:﹣2,5,﹣2≤t≤5.
16.(1)x+2x≥0;
(2)设炮弹的杀伤半径为r,则应有r≥300;
(3)设每件上衣为a元,每条长裤是b元,应有3a+4b≤368;
(4)用P表示明天下雨的可能性,则有P≥70%;
(5)设小明的体重为a千克,小亮的体重为b千克,则应有a≥b.
17.解:(1)﹣π<﹣3;
(2)a2≥0;
(3)∵x,y的值不确定∴|x|+|y|≥|x+y|;
(4)(﹣5)÷(﹣1)=5>(﹣6)÷(﹣7)=;
(5)当a≤0时,|a|=﹣a.
18.解:由数轴可得m<n<0,
(1)两个负数相加,和仍为负数,故m+n<0;
(2)相当于两个异号的数相加,符号由绝对值大的数决定,故m﹣n<0;
(3)两个负数的积是正数,故m n>0;
(4)正数大于一切负数,故m2>n;
(5)由数轴离原点的距离可得,|m|>|n|.
19.解:(1)x+2x≤0;
(2)设炮弹的杀伤半径为r,则应有r≥300;
(3)设每件上衣为a元,每条长裤是b元,应有3a+4b≤268;
(4)用P表示明天下雨的可能性,则有P≥70%;
(5)设小明的体重为a千克,小刚的体重为b千克,则应有a≥b.
20.由题意可知,限重、限宽、限高、限速中的“限”字的意义就是不超过,也就是“≤”的意义,即:x≤5.5t,y≤30km/h,l≤2m,h≤3.5m.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
