第八章 平行线的有关证明 单元测试题(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 单元测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《第八章 平行线的有关证明》
单元测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.下列说法错误的是( )
A.所有命题都是定理 B.定理是真命题
C.公理是真命题 D.“画线段AB=CD”不是命题
2.有下列命题:①两点之间的所有连线中,线段最短;②相等的角是对顶角;③过直线外一点有且仅有一条直线与已知直线平行;④两点之间的距离是两点间的线段;⑤如果一个角的两边与另一个角的两边互相垂直,那么这两个角相等.其中,是真命题的有( )
A.1个 B.2个 C.3个 D.4个
3.阅读下面的材料:
如图,直线b//c,a⊥b,求证:a⊥c.
证明:①∵a⊥b(已知)∴∠1=90°(垂直的定义).
②又∵b//c(已知),∴∠1=∠2(同位角相等,两直线平行).
③∴∠2=∠1=90°(等量代换).
④∴a⊥c(垂直的定义).
其①~④步中数学依据错误的是( )
A.① B.② C.③ D.④
4.如图,AB//CD,∠B=75°,∠E=27°,则∠D的度数为( )
A.58° B.50° C.48° D.45°
第4题图 第5题图
5.如图,直线m∥n,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分.若∠1=60°,则下列结论错误的是 ( )
A.∠2=75° B.∠3=45° C.∠4=105° D.∠5=130°
6.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容:
已知:如图,∠BEC=∠B+∠C.求证:AB//CD.
证明:延长BE交 ※ 于点F,则∠BEC= ◎ +∠C(三角形的外角等于与它不相邻两个内角之和).
又∠BEC=∠B+∠C,得∠B= ▲ .
故AB//CD( @ 相等,两直线平行).
则回答正确的是( )
A.◎代表∠FEC B.@代表同位角 C.▲代表∠EFC D.※代表AB
7.举反例说明“一个角的余角大于这个角”是假命题,下列举例错误的是( )
A.设这个角是45°,它的余角是45°,但
B.设这个角是30°,它的余角是60°,但30°<60°
C.设这个角是60°,它的余角是30°,但30°<60°
D.设这个角是50°,它的余角是40°,但
8.如图,将△ABC沿MN折叠,使MN∥BC,点A的对应点为A′.若∠A′=32°,∠B=112°.则∠A′NC的度数是( )
A.114° B.112° C.110° D.108°
第8题图 第9题图 第10题图
9.如图,有下列条件:①∠1=∠2;②∠C=∠D;③∠A=∠F.从这三个条件中选出两个作为已知条件,另一个作为结论组成命题,则在所组成的命题中,正确命题的个数为( )
A.0 B.1 C.2 D.3
10.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG//CE,交AB于点G.若 则∠3的度数为( )
A.30° B.40° C.45° D.70°
二、填空题(每小题3分,共18分)
11.命题“不相等的两个角不是直角”的条件是______________,结论是_______________.
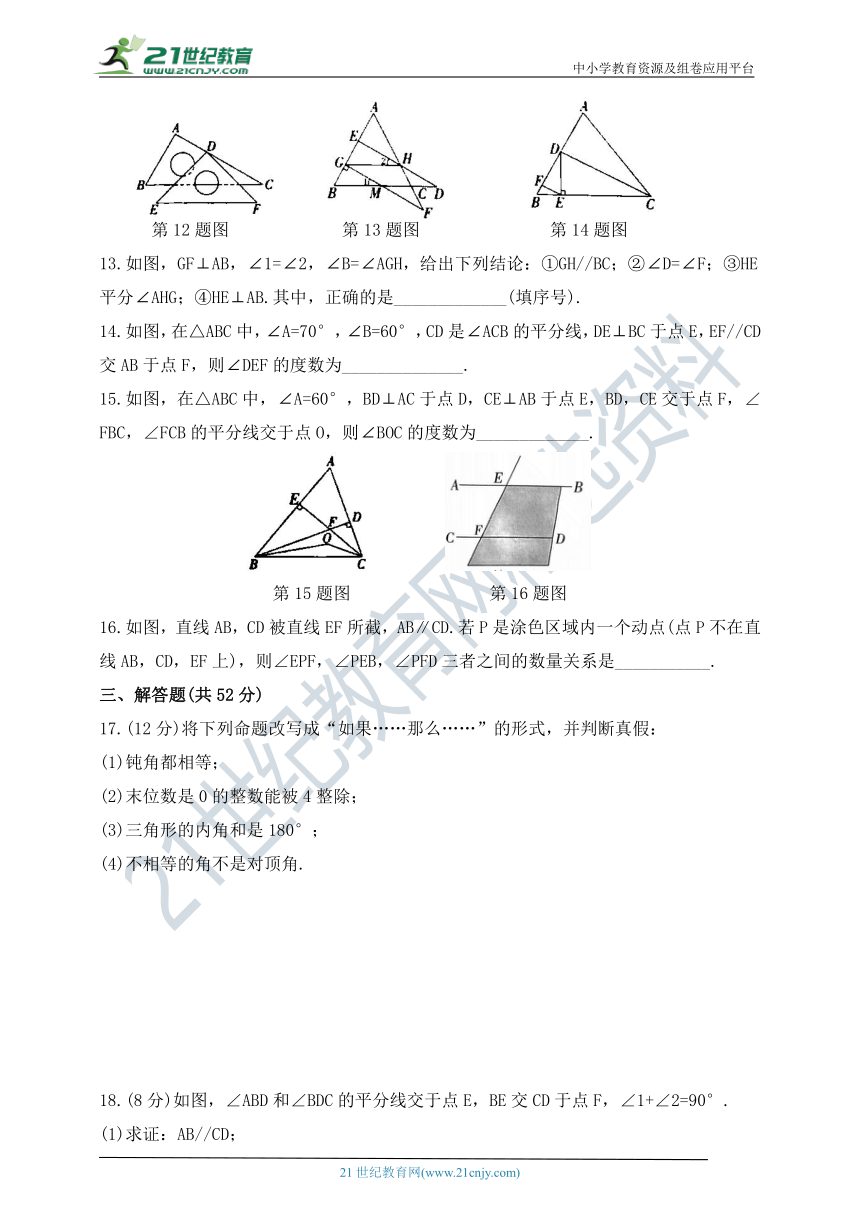
12.将一副三角尺按如图所示的方式摆放,点D在边AC上,BC//EF,则∠ADE的度数为____________.
第12题图 第13题图 第14题图
13.如图,GF⊥AB,∠1=∠2,∠B=∠AGH,给出下列结论:①GH//BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB.其中,正确的是_____________(填序号).
14.如图,在△ABC中,∠A=70°,∠B=60°,CD是∠ACB的平分线,DE⊥BC于点E,EF//CD交AB于点F,则∠DEF的度数为______________.
15.如图,在△ABC中,∠A=60°,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,∠FBC,∠FCB的平分线交于点O,则∠BOC的度数为_____________.
第15题图 第16题图
16.如图,直线AB,CD被直线EF所截,AB∥CD.若P是涂色区域内一个动点(点P不在直线AB,CD,EF上),则∠EPF,∠PEB,∠PFD三者之间的数量关系是___________.
三、解答题(共52分)
17.(12分)将下列命题改写成“如果……那么……”的形式,并判断真假:
(1)钝角都相等;
(2)末位数是0的整数能被4整除;
(3)三角形的内角和是180°;
(4)不相等的角不是对顶角.
18.(8分)如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)求证:AB//CD;
(2)试探究∠2与∠3的数量关系.
19.(8分)如图,在△ABC中,∠A=50°,点M在AB上,过点M作MN//BC,交AC于点N,D是AN上一点,连接DM并延长,交CB的延长线于点E.
(1)若∠ABE=110°,∠MDN=70°,求∠GEF的度数;
(2)求证:∠DEG-∠DNM=∠A+∠EMB.
20.(12分)如图,在△ABC中,∠BAC=50°,I是∠ABC,∠ACB平分线的交点.
(1)∠BIC=_________°.
(2)若D是两条外角平分线的交点,则∠BDC=___________°.
(3)在(2)的条件下,若E是内角∠ABC和外角∠ACG的平分线的交点,试探索∠BEC与∠BAC的数量关系,并说明理由.
(4)在(3)的条件下,当△ACB为多少度时,CE/AB 请说明理由.
21.(12分)已知点E在直线AB上,点F在直线CD上,EG⊥FG.
(1)如图①,若∠BEG+∠DFG=90°,请判断AB与CD的位置关系,并说明理由.
(2)如图②,在(1)的结论下,当EG⊥FG保持不变,EG上有一点M,使∠MFG=2∠DFG,则∠BEG与∠MFD存在怎样的数量关系 请说明理由.
(3)在图②的基础上,若移动点M,使∠MFG=n∠DFG,请直接写出∠BEG与∠MFD的数量关系.
参考答案
一、1.A 2.B 3.B 4.C 5.D 6.C 7.B 8.D 9.D 10.B
二、11.两个角不相等 这两个角不是直角 12. 75° 13.①④ 14.65° 15.150° 16.∠EPF=∠PEB+∠PFD或∠EPF=∠PEB-∠PFD
三、17.(1)如果几个角都是钝角,那么这几个角相等 假命题
(2)如果一个整数的末位数是0,那么它能被4整除 假命题
(3)如果一个图形是三角形,那么它的内角和是180° 真命题
(4)如果两个角不相等,那么这两个角不是对顶角 真命题
18.(1)∵BE,DE分别平分∠ABD,∠BDC,∴∠1=∠BDC.
∵∠1+∠2=90°,∴∠ABD+∠BDC=180°.∴AB∥CD
(2)∵DE平分∠BDC,∴∠2=∠FDE.∵∠1+∠2=90°,∴∠BED=180°-(∠1+∠2)=90°=∠DEF.∴∠3+∠FDE=90°.∴∠2+∠3=90°
19.(1)∵∠ABE=110°,∠A=50°,∴∠C=∠ABE-∠A=60°.∵MN∥BC,∴∠DNM=∠C=60°.∵∠MDN=70°,∴∠DMN=180°-∠MDN-∠DNM=50°.
∵MN∥BC,∴∠MEB=∠DMN=50°.∴∠GEF=∠MEB=50°
(2)∵∠DEG=∠MDN+∠C,∠MDN=∠A+∠AMD,∴∠DEG=∠A+∠AMD+∠C.
∵MN∥BC,∴∠DNM=∠C.∵∠EMB=∠AMD,∴∠DEG=∠A+∠EMB+∠DNM,
即∠DEG-∠DNM=∠A+∠EMB
20.(1) 115 (2) 65
理由:∵BE平分∠ABC,DB平分∠GBF,∴∠ABC,
∴90°.
∵D是两条外角平分线的交点,∴
又∵∠CBF+∠BCM=∠BAC+∠ACB+∠BAC+ ∴∠BDC=180°-(∠BCD)=∴∠BEC= (4)当∠ACB=80°时,CE∥AB 理由:∵CE∥AB,∴∠ACE=∠A=50°.∵CE是∠ACG的平分线,∴∠ACG=2∠ACE=100°.∴∠ACB=180°-∠ACG=180°-100°=80°.
21.(1)AB∥CD 理由:如图①,延长EG交CD于点H.∵EG⊥FG,∴∠HGF=∠EGF=90°.
∴∠GHF+∠GFH=90°.∵∠BEG+∠DFG=90°,∴∠BEG=∠GHF.∴AB∥CD.
理由:如图②,延长EG交CD于点H.
∵AB∥CD,∴∠BEG=∠GHF.∵EG⊥FG,∴∠GHF+∠GFH=90°.
∵∠MFG=2∠DFG,∴∴
°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《第八章 平行线的有关证明》
单元测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.下列说法错误的是( )
A.所有命题都是定理 B.定理是真命题
C.公理是真命题 D.“画线段AB=CD”不是命题
2.有下列命题:①两点之间的所有连线中,线段最短;②相等的角是对顶角;③过直线外一点有且仅有一条直线与已知直线平行;④两点之间的距离是两点间的线段;⑤如果一个角的两边与另一个角的两边互相垂直,那么这两个角相等.其中,是真命题的有( )
A.1个 B.2个 C.3个 D.4个
3.阅读下面的材料:
如图,直线b//c,a⊥b,求证:a⊥c.
证明:①∵a⊥b(已知)∴∠1=90°(垂直的定义).
②又∵b//c(已知),∴∠1=∠2(同位角相等,两直线平行).
③∴∠2=∠1=90°(等量代换).
④∴a⊥c(垂直的定义).
其①~④步中数学依据错误的是( )
A.① B.② C.③ D.④
4.如图,AB//CD,∠B=75°,∠E=27°,则∠D的度数为( )
A.58° B.50° C.48° D.45°
第4题图 第5题图
5.如图,直线m∥n,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分.若∠1=60°,则下列结论错误的是 ( )
A.∠2=75° B.∠3=45° C.∠4=105° D.∠5=130°
6.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容:
已知:如图,∠BEC=∠B+∠C.求证:AB//CD.
证明:延长BE交 ※ 于点F,则∠BEC= ◎ +∠C(三角形的外角等于与它不相邻两个内角之和).
又∠BEC=∠B+∠C,得∠B= ▲ .
故AB//CD( @ 相等,两直线平行).
则回答正确的是( )
A.◎代表∠FEC B.@代表同位角 C.▲代表∠EFC D.※代表AB
7.举反例说明“一个角的余角大于这个角”是假命题,下列举例错误的是( )
A.设这个角是45°,它的余角是45°,但
B.设这个角是30°,它的余角是60°,但30°<60°
C.设这个角是60°,它的余角是30°,但30°<60°
D.设这个角是50°,它的余角是40°,但
8.如图,将△ABC沿MN折叠,使MN∥BC,点A的对应点为A′.若∠A′=32°,∠B=112°.则∠A′NC的度数是( )
A.114° B.112° C.110° D.108°
第8题图 第9题图 第10题图
9.如图,有下列条件:①∠1=∠2;②∠C=∠D;③∠A=∠F.从这三个条件中选出两个作为已知条件,另一个作为结论组成命题,则在所组成的命题中,正确命题的个数为( )
A.0 B.1 C.2 D.3
10.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG//CE,交AB于点G.若 则∠3的度数为( )
A.30° B.40° C.45° D.70°
二、填空题(每小题3分,共18分)
11.命题“不相等的两个角不是直角”的条件是______________,结论是_______________.
12.将一副三角尺按如图所示的方式摆放,点D在边AC上,BC//EF,则∠ADE的度数为____________.
第12题图 第13题图 第14题图
13.如图,GF⊥AB,∠1=∠2,∠B=∠AGH,给出下列结论:①GH//BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB.其中,正确的是_____________(填序号).
14.如图,在△ABC中,∠A=70°,∠B=60°,CD是∠ACB的平分线,DE⊥BC于点E,EF//CD交AB于点F,则∠DEF的度数为______________.
15.如图,在△ABC中,∠A=60°,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,∠FBC,∠FCB的平分线交于点O,则∠BOC的度数为_____________.
第15题图 第16题图
16.如图,直线AB,CD被直线EF所截,AB∥CD.若P是涂色区域内一个动点(点P不在直线AB,CD,EF上),则∠EPF,∠PEB,∠PFD三者之间的数量关系是___________.
三、解答题(共52分)
17.(12分)将下列命题改写成“如果……那么……”的形式,并判断真假:
(1)钝角都相等;
(2)末位数是0的整数能被4整除;
(3)三角形的内角和是180°;
(4)不相等的角不是对顶角.
18.(8分)如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)求证:AB//CD;
(2)试探究∠2与∠3的数量关系.
19.(8分)如图,在△ABC中,∠A=50°,点M在AB上,过点M作MN//BC,交AC于点N,D是AN上一点,连接DM并延长,交CB的延长线于点E.
(1)若∠ABE=110°,∠MDN=70°,求∠GEF的度数;
(2)求证:∠DEG-∠DNM=∠A+∠EMB.
20.(12分)如图,在△ABC中,∠BAC=50°,I是∠ABC,∠ACB平分线的交点.
(1)∠BIC=_________°.
(2)若D是两条外角平分线的交点,则∠BDC=___________°.
(3)在(2)的条件下,若E是内角∠ABC和外角∠ACG的平分线的交点,试探索∠BEC与∠BAC的数量关系,并说明理由.
(4)在(3)的条件下,当△ACB为多少度时,CE/AB 请说明理由.
21.(12分)已知点E在直线AB上,点F在直线CD上,EG⊥FG.
(1)如图①,若∠BEG+∠DFG=90°,请判断AB与CD的位置关系,并说明理由.
(2)如图②,在(1)的结论下,当EG⊥FG保持不变,EG上有一点M,使∠MFG=2∠DFG,则∠BEG与∠MFD存在怎样的数量关系 请说明理由.
(3)在图②的基础上,若移动点M,使∠MFG=n∠DFG,请直接写出∠BEG与∠MFD的数量关系.
参考答案
一、1.A 2.B 3.B 4.C 5.D 6.C 7.B 8.D 9.D 10.B
二、11.两个角不相等 这两个角不是直角 12. 75° 13.①④ 14.65° 15.150° 16.∠EPF=∠PEB+∠PFD或∠EPF=∠PEB-∠PFD
三、17.(1)如果几个角都是钝角,那么这几个角相等 假命题
(2)如果一个整数的末位数是0,那么它能被4整除 假命题
(3)如果一个图形是三角形,那么它的内角和是180° 真命题
(4)如果两个角不相等,那么这两个角不是对顶角 真命题
18.(1)∵BE,DE分别平分∠ABD,∠BDC,∴∠1=∠BDC.
∵∠1+∠2=90°,∴∠ABD+∠BDC=180°.∴AB∥CD
(2)∵DE平分∠BDC,∴∠2=∠FDE.∵∠1+∠2=90°,∴∠BED=180°-(∠1+∠2)=90°=∠DEF.∴∠3+∠FDE=90°.∴∠2+∠3=90°
19.(1)∵∠ABE=110°,∠A=50°,∴∠C=∠ABE-∠A=60°.∵MN∥BC,∴∠DNM=∠C=60°.∵∠MDN=70°,∴∠DMN=180°-∠MDN-∠DNM=50°.
∵MN∥BC,∴∠MEB=∠DMN=50°.∴∠GEF=∠MEB=50°
(2)∵∠DEG=∠MDN+∠C,∠MDN=∠A+∠AMD,∴∠DEG=∠A+∠AMD+∠C.
∵MN∥BC,∴∠DNM=∠C.∵∠EMB=∠AMD,∴∠DEG=∠A+∠EMB+∠DNM,
即∠DEG-∠DNM=∠A+∠EMB
20.(1) 115 (2) 65
理由:∵BE平分∠ABC,DB平分∠GBF,∴∠ABC,
∴90°.
∵D是两条外角平分线的交点,∴
又∵∠CBF+∠BCM=∠BAC+∠ACB+∠BAC+ ∴∠BDC=180°-(∠BCD)=∴∠BEC= (4)当∠ACB=80°时,CE∥AB 理由:∵CE∥AB,∴∠ACE=∠A=50°.∵CE是∠ACG的平分线,∴∠ACG=2∠ACE=100°.∴∠ACB=180°-∠ACG=180°-100°=80°.
21.(1)AB∥CD 理由:如图①,延长EG交CD于点H.∵EG⊥FG,∴∠HGF=∠EGF=90°.
∴∠GHF+∠GFH=90°.∵∠BEG+∠DFG=90°,∴∠BEG=∠GHF.∴AB∥CD.
理由:如图②,延长EG交CD于点H.
∵AB∥CD,∴∠BEG=∠GHF.∵EG⊥FG,∴∠GHF+∠GFH=90°.
∵∠MFG=2∠DFG,∴∴
°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
