2021-2022学年沪科版数学七年级下册7.3一元一次不等式组(第一课时)课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级下册7.3一元一次不等式组(第一课时)课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 389.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
7.3 一元一次不等式组
沪科版数学七年级下
第一课时
设该校计划每月烧煤x吨,根据题意,得
未知数x同时满足① ②两个条件,把① ②两个不等
式合在一起,就组成一个一元一次不等式组,记作:
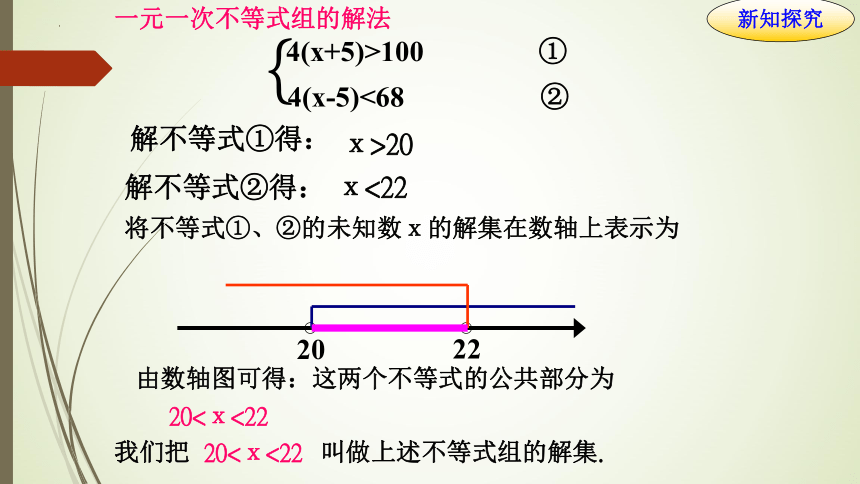
4(x+5)>100 ①
且 4(x-5)<68 ②
4(x+5)>100
4(x-5)<68
{
某校今年冬季烧煤取暖时间为4个月.如果每个月比计划多烧5吨煤, 那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨,该校计划每月烧煤多少吨
新知导入
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个。
两个或两个以上含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组。
一元一次不等式组定义:
新知讲解
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
4(x+5)>100 ①
4(x-5)<68 ②
{
解不等式①得:
x>20
解不等式②得:
x<22
20
22
将不等式①、②的未知数x的解集在数轴上表示为
一元一次不等式组的解法
由数轴图可得:这两个不等式的公共部分为
20<x<22
我们把 叫做上述不等式组的解集.
20<x<22
新知探究
不等式组的解集:
不等式组中所有不等式的解集的公共部分叫做不等式组的解集
求不等式组解集的过程叫做 解不等式组
解不等式组
2
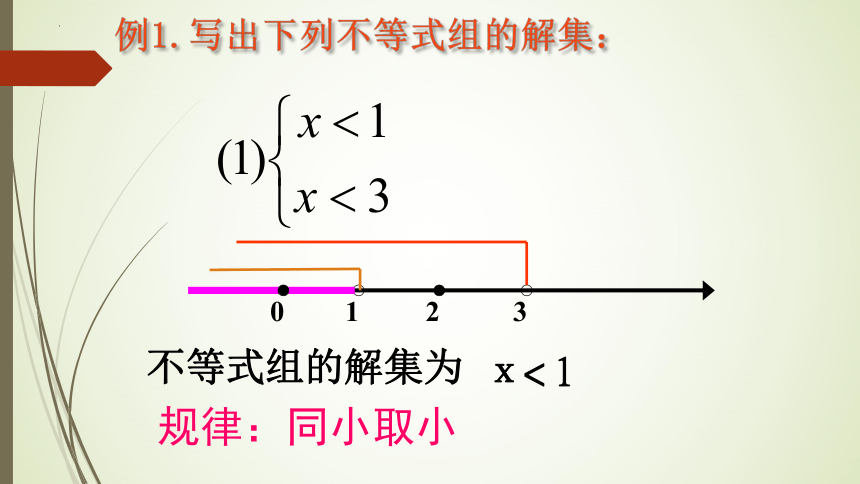
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
x< 1
规律:同小取小
2
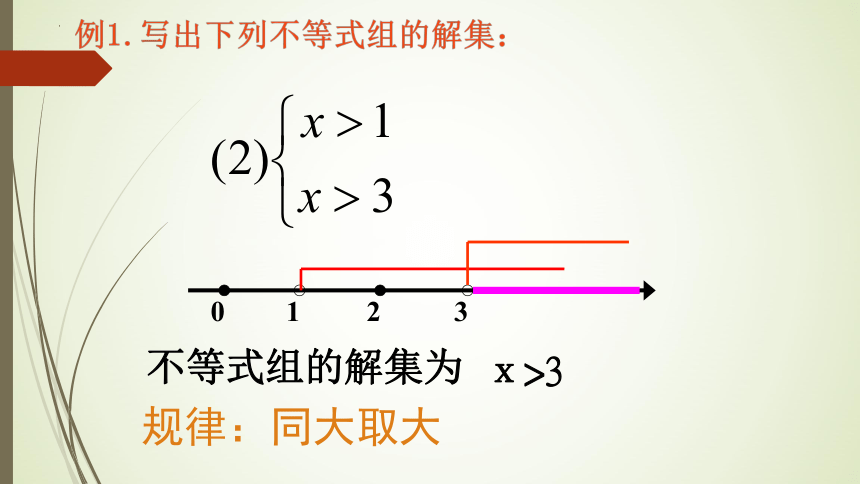
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
x>3
规律:同大取大
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
1<x< 3
规律:大小小大中间找
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为空集
即:不等式组无解
规律:大大小小找不到
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
解集为 : x<a
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
解集为:无解
(同大取大)
(同小取小)
(大小小大中间找)
(大大小小找不到)
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 大大取较大,
2.小小取较小;
3.大小小大取中间,
4.大大小小解不了。
x>2
x>-2
x<3
x<-4
3-1无解
无解
-2≤x<1
x≤-2
x<-2
x>2
0 1 2 3 4
例1:解下列不等式组
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
⑴
②
①
⑵
②
①
所以不等式组的解集:
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解.
-1 0 1 2 3
解一元一次不等式组的方法:
2.(1)利用数轴找几个解集的公共部分:
(2)利用规律: 大大取较大,小小取较小;大小小大取中间,大大小小解不了。
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
归纳:不等式组的解法是
分开解,借数轴,集中判
0 2 10 20 30 48 50
例题讲解
例2、解下列不等式组
⑴
②
①
⑵
②
①
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式的解集:
0 15
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式组无解
例3、解不等式组:
①
②
解:解不等式①,得
解不等式②,得
不等式组的解集是
2
0
4
2.5
1
3
例题讲解
0
8
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
例题讲解
1、选择题:
(1)不等式组 的解集是( )
A.x ≥2,
D.x =2.
B.x≤2,
C. 无解,
(2)不等式组 的整数解是( )
≤1
D. x≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
D
C
≥2
≤2
课堂练习
D.不能确定.
A. -2, 0, -1 ,
B. -2
C. -2, -1,
(3)不等式组 的负整数解是( )
≥-2,
(4)不等式组 的解集在数轴上
表示为 ( )
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
4.选择题:
(1)不等式组 的解集是( )
A.x<1
B.x ≥ 2
C. 1D. 无解
A.1
B.2
C.0
D.–1
D
C
A.x>b
B.xC.无解
D.aC
A
1.解下列不等式组:
解:(1) 1<x<5;
(2)-4<x≤1;
(3) x< ;
(4) 无解.
课堂练习
拓展 练习1
试求不等式组 的解集.
解:解不等式①,得 x > - 2
解不等式②,得 x > 3
解不等式③,得 x ≤ 6
把不等式①、②、③的解集表示在同一数轴上,如下图
-2 -1 0 1 2 3 4 5 6
○
●
○
所以,不等式组的解集是3 < x ≤ 6.
动手画一画,一起找一找.
若︱x+1︱= x+1,︱3x+2︱=-3x-2,
则x的取值范围是_______
-1≤x≤
2
3
解: 由题意,得
{
X+1≥0
-3x-2≥0
由①得 x≥-1
由② 得
x≤
2
3
①
②
所以这个不等式组的解集是
-1≤x≤
2
3
拓展 练习2
1. 由几个含有相同未知数的一元一次不等式所组成的不等式组叫做一元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
课堂总结
7.3 一元一次不等式组
沪科版数学七年级下
第一课时
设该校计划每月烧煤x吨,根据题意,得
未知数x同时满足① ②两个条件,把① ②两个不等
式合在一起,就组成一个一元一次不等式组,记作:
4(x+5)>100 ①
且 4(x-5)<68 ②
4(x+5)>100
4(x-5)<68
{
某校今年冬季烧煤取暖时间为4个月.如果每个月比计划多烧5吨煤, 那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨,该校计划每月烧煤多少吨
新知导入
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个。
两个或两个以上含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组。
一元一次不等式组定义:
新知讲解
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
4(x+5)>100 ①
4(x-5)<68 ②
{
解不等式①得:
x>20
解不等式②得:
x<22
20
22
将不等式①、②的未知数x的解集在数轴上表示为
一元一次不等式组的解法
由数轴图可得:这两个不等式的公共部分为
20<x<22
我们把 叫做上述不等式组的解集.
20<x<22
新知探究
不等式组的解集:
不等式组中所有不等式的解集的公共部分叫做不等式组的解集
求不等式组解集的过程叫做 解不等式组
解不等式组
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
x< 1
规律:同小取小
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
x>3
规律:同大取大
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为
1<x< 3
规律:大小小大中间找
2
例1.写出下列不等式组的解集:
1
3
0
不等式组的解集为空集
即:不等式组无解
规律:大大小小找不到
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
解集为 : x<a
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
解集为:无解
(同大取大)
(同小取小)
(大小小大中间找)
(大大小小找不到)
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 大大取较大,
2.小小取较小;
3.大小小大取中间,
4.大大小小解不了。
x>2
x>-2
x<3
x<-4
3
无解
-2≤x<1
x≤-2
x<-2
x>2
0 1 2 3 4
例1:解下列不等式组
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
⑴
②
①
⑵
②
①
所以不等式组的解集:
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解.
-1 0 1 2 3
解一元一次不等式组的方法:
2.(1)利用数轴找几个解集的公共部分:
(2)利用规律: 大大取较大,小小取较小;大小小大取中间,大大小小解不了。
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
归纳:不等式组的解法是
分开解,借数轴,集中判
0 2 10 20 30 48 50
例题讲解
例2、解下列不等式组
⑴
②
①
⑵
②
①
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式的解集:
0 15
解:解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
所以不等式组无解
例3、解不等式组:
①
②
解:解不等式①,得
解不等式②,得
不等式组的解集是
2
0
4
2.5
1
3
例题讲解
0
8
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
例题讲解
1、选择题:
(1)不等式组 的解集是( )
A.x ≥2,
D.x =2.
B.x≤2,
C. 无解,
(2)不等式组 的整数解是( )
≤1
D. x≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
D
C
≥2
≤2
课堂练习
D.不能确定.
A. -2, 0, -1 ,
B. -2
C. -2, -1,
(3)不等式组 的负整数解是( )
≥-2,
(4)不等式组 的解集在数轴上
表示为 ( )
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
4.选择题:
(1)不等式组 的解集是( )
A.x<1
B.x ≥ 2
C. 1
A.1
B.2
C.0
D.–1
D
C
A.x>b
B.x
D.a
A
1.解下列不等式组:
解:(1) 1<x<5;
(2)-4<x≤1;
(3) x< ;
(4) 无解.
课堂练习
拓展 练习1
试求不等式组 的解集.
解:解不等式①,得 x > - 2
解不等式②,得 x > 3
解不等式③,得 x ≤ 6
把不等式①、②、③的解集表示在同一数轴上,如下图
-2 -1 0 1 2 3 4 5 6
○
●
○
所以,不等式组的解集是3 < x ≤ 6.
动手画一画,一起找一找.
若︱x+1︱= x+1,︱3x+2︱=-3x-2,
则x的取值范围是_______
-1≤x≤
2
3
解: 由题意,得
{
X+1≥0
-3x-2≥0
由①得 x≥-1
由② 得
x≤
2
3
①
②
所以这个不等式组的解集是
-1≤x≤
2
3
拓展 练习2
1. 由几个含有相同未知数的一元一次不等式所组成的不等式组叫做一元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
课堂总结
