2021-2022学年华东师大版九年级数学下册27.2 第2课时 直线与圆的位置关系 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册27.2 第2课时 直线与圆的位置关系 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
请在此处输入文字
27.2 直线与圆的位置关系
第2课时
ZHI XIAN YU YUAN DE WEI ZHI GUAN XI
1.了解直线与圆的位置关系
Learning objectives
学习目标
2.根据定义来判断直线与圆的
位置关系
3.根据圆心到直线的距离与圆
的半径之间的数量关系,判定
直线与圆的位置关系.
知识回顾
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 dA
B
C
情境导入
世界上不是缺少美,而是缺少发现美的眼睛。我们要学会从生活中发现数学的“美”,并用“美”的数学为我们的生活服务。下面请同学们欣赏美丽的海上日出。
思考:从海上日出这种自然现象中,可以抽象出哪些平面图形?
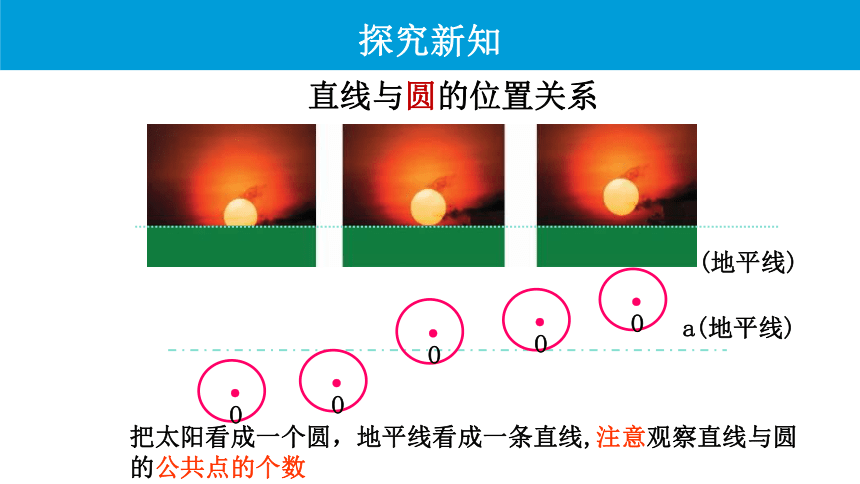
直线与圆的位置关系
(地平线)
a(地平线)
●O
●O
●O
●O
●O
探究新知
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
特点:
叫做直线和圆相交。
直线和圆有两个公共点,
特点:
直线和圆有惟一的公共点,
叫做直线和圆相切。
这时的直线叫切线
惟一的公共点叫切点。
特点:
直线和圆没有公共点,
叫直线和圆相离
.A
.A
.B
C
一、直线与圆的位置关系(用公共点的个数来区分)
探究新知
相交
相切
相离
1、在这个变化过程中,除了公共点的个数发生了变化,还有什么量在改变?
2、你能否用数量关系来判定直线与圆的位置关系?
3、如何用数量关系描述直线与圆的位置关系?
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
二、直线和圆的位置关系(用圆心o到直线l的距离d与圆的半径r的关系来区分)
易错警示
(1)理解切线定义时,要抓住关键字眼“只有一个”,避免
出现“有一个公共点时,直线和圆相切”的错误,用
动态的观点及数形结合思想来准确理解切线的定义.
(2)射线、线段和圆的位置关系不能像直线一样依据交点
个数判定,要具体情况具体分析.
师生小结
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
割线
1个
切点
切线
0个
相离
相切
相交
数量关系
d> r
d= r
d﹤r
∟
r
d
∟
r
d
r
d
2个
交点
三、例题讲解巩固新知
例1 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,以C为圆心,分别以下面的r为半径画圆,那么圆与斜边AB所在的直线有怎样的位置关系呢?
(1) r=4; (2) r=4.8; (3) r=5.
A
C
B
8
6
D
分析:要了解AB与☉C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
10.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=4.8.
所以 (1)当r=4时,有d >r,
☉C和AB相离.
A
C
B
8
6
D
d
(2)当r=4.8时,有d=r,
☉C和AB相切.
(3)当r=5时,有d☉C和AB相交.
四、反馈练习 检验新知
1.已知圆的半径为6cm,圆心到直线的距离为d :
(1)若d=4cm ,则直线与圆 ,直线与圆有____个公共点.
(2)若d=6cm ,则直线与圆______, 直线与圆有___个公共点.
(3)若d=8cm ,则直线与圆______, 直线与圆有___ 个公共点.
(3)若AB和☉O相交,则 .
2.已知☉O的半径为5cm, 圆心到直线AB的距离为d, 根据条件判断d的取值范围:
(1)若AB和☉O相离, 则 ;
(2)若AB和☉O相切, 则 ;
相交
2
相切
相离
d > 5cm
d = 5cm
0cm≤ d < 5cm
0
1
3. 已知⊙A的直径为6 cm ,点A的坐标为(-3,-4),则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。
A.(-3,-4)
O
X
Y
B
C
4
3
相离
相切
思考:求圆心A到X轴、
Y轴的距离各是多少
生活中的直线与圆的位置关系
相
切
相
交
相
交
相
离
1、直线与圆的位置关系3种:相离、相切和相交。
2、识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
五、课堂小结
六、分层作业 选优拔高
高分突破相关练习题
选做题
必做题
你知道圆与圆的位置关系吗?
谢谢大家!
请在此处输入文字
27.2 直线与圆的位置关系
第2课时
ZHI XIAN YU YUAN DE WEI ZHI GUAN XI
1.了解直线与圆的位置关系
Learning objectives
学习目标
2.根据定义来判断直线与圆的
位置关系
3.根据圆心到直线的距离与圆
的半径之间的数量关系,判定
直线与圆的位置关系.
知识回顾
点和圆的位置关系有几种?
点到圆心的距离为d,圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
B
C
情境导入
世界上不是缺少美,而是缺少发现美的眼睛。我们要学会从生活中发现数学的“美”,并用“美”的数学为我们的生活服务。下面请同学们欣赏美丽的海上日出。
思考:从海上日出这种自然现象中,可以抽象出哪些平面图形?
直线与圆的位置关系
(地平线)
a(地平线)
●O
●O
●O
●O
●O
探究新知
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
特点:
叫做直线和圆相交。
直线和圆有两个公共点,
特点:
直线和圆有惟一的公共点,
叫做直线和圆相切。
这时的直线叫切线
惟一的公共点叫切点。
特点:
直线和圆没有公共点,
叫直线和圆相离
.A
.A
.B
C
一、直线与圆的位置关系(用公共点的个数来区分)
探究新知
相交
相切
相离
1、在这个变化过程中,除了公共点的个数发生了变化,还有什么量在改变?
2、你能否用数量关系来判定直线与圆的位置关系?
3、如何用数量关系描述直线与圆的位置关系?
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
二、直线和圆的位置关系(用圆心o到直线l的距离d与圆的半径r的关系来区分)
易错警示
(1)理解切线定义时,要抓住关键字眼“只有一个”,避免
出现“有一个公共点时,直线和圆相切”的错误,用
动态的观点及数形结合思想来准确理解切线的定义.
(2)射线、线段和圆的位置关系不能像直线一样依据交点
个数判定,要具体情况具体分析.
师生小结
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
割线
1个
切点
切线
0个
相离
相切
相交
数量关系
d> r
d= r
d﹤r
∟
r
d
∟
r
d
r
d
2个
交点
三、例题讲解巩固新知
例1 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,以C为圆心,分别以下面的r为半径画圆,那么圆与斜边AB所在的直线有怎样的位置关系呢?
(1) r=4; (2) r=4.8; (3) r=5.
A
C
B
8
6
D
分析:要了解AB与☉C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB=
10.
根据三角形的面积公式有
∴
即圆心C到AB的距离d=4.8.
所以 (1)当r=4时,有d >r,
☉C和AB相离.
A
C
B
8
6
D
d
(2)当r=4.8时,有d=r,
☉C和AB相切.
(3)当r=5时,有d
四、反馈练习 检验新知
1.已知圆的半径为6cm,圆心到直线的距离为d :
(1)若d=4cm ,则直线与圆 ,直线与圆有____个公共点.
(2)若d=6cm ,则直线与圆______, 直线与圆有___个公共点.
(3)若d=8cm ,则直线与圆______, 直线与圆有___ 个公共点.
(3)若AB和☉O相交,则 .
2.已知☉O的半径为5cm, 圆心到直线AB的距离为d, 根据条件判断d的取值范围:
(1)若AB和☉O相离, 则 ;
(2)若AB和☉O相切, 则 ;
相交
2
相切
相离
d > 5cm
d = 5cm
0cm≤ d < 5cm
0
1
3. 已知⊙A的直径为6 cm ,点A的坐标为(-3,-4),则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。
A.(-3,-4)
O
X
Y
B
C
4
3
相离
相切
思考:求圆心A到X轴、
Y轴的距离各是多少
生活中的直线与圆的位置关系
相
切
相
交
相
交
相
离
1、直线与圆的位置关系3种:相离、相切和相交。
2、识别直线与圆的位置关系的方法:
(1)一种是根据定义进行识别:
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
五、课堂小结
六、分层作业 选优拔高
高分突破相关练习题
选做题
必做题
你知道圆与圆的位置关系吗?
谢谢大家!
