沪科版数学八上16.3等腰三角形的性质
文档属性
| 名称 | 沪科版数学八上16.3等腰三角形的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 392.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-15 00:00:00 | ||
图片预览



文档简介
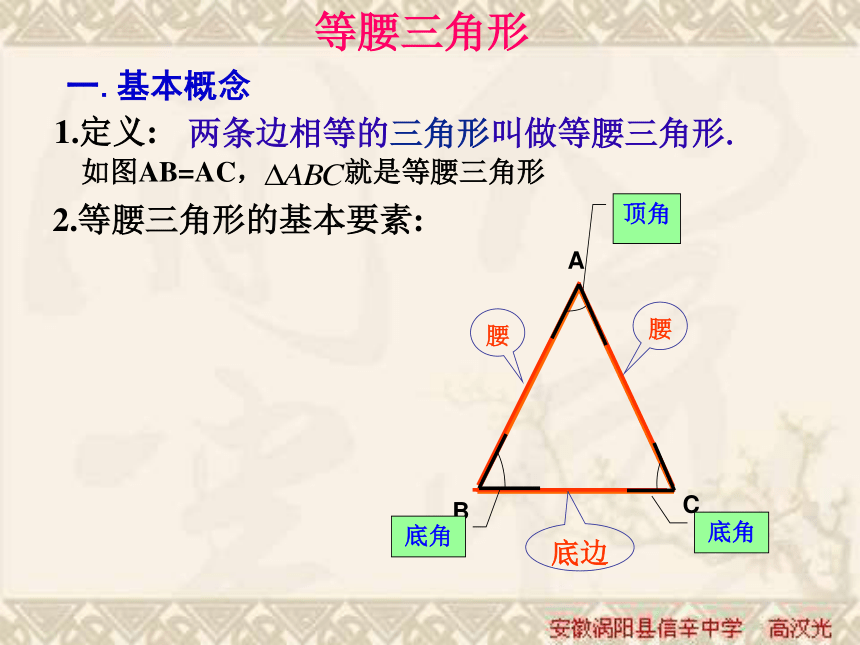
课件26张PPT。 16.3等腰三角形的性质 等腰三角形一.基本概念 1.定义:两条边相等的三角形叫做等腰三角形. 如图AB=AC, 就是等腰三角形 2.等腰三角形的基本要素:操作: 现在请同学们将所画的等腰三角形对折,
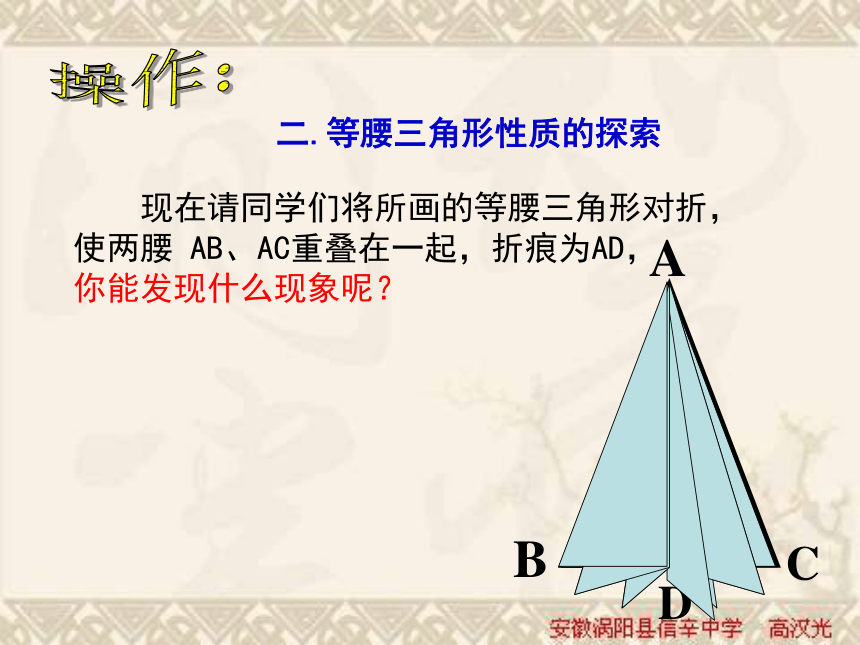
使两腰 AB、AC重叠在一起,折痕为AD,
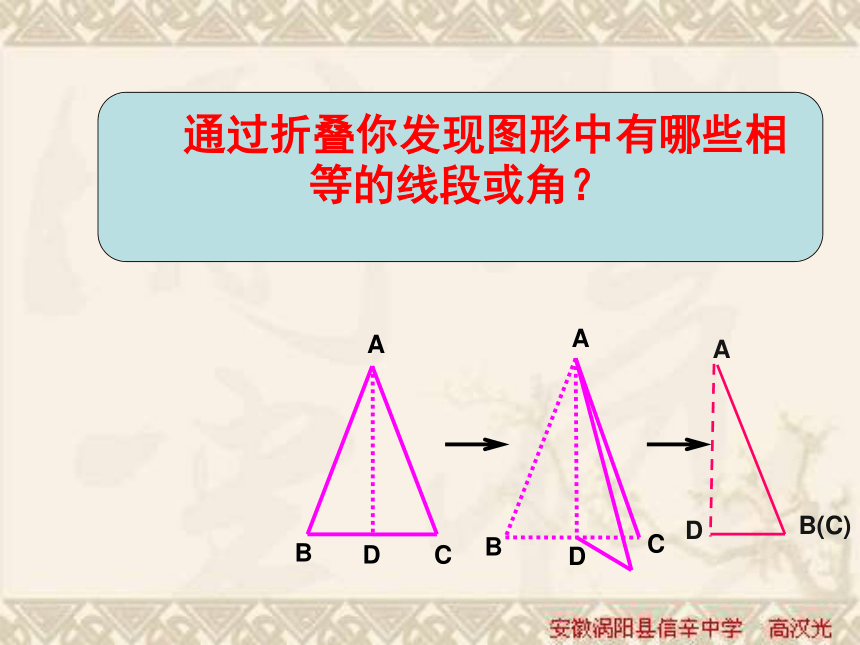
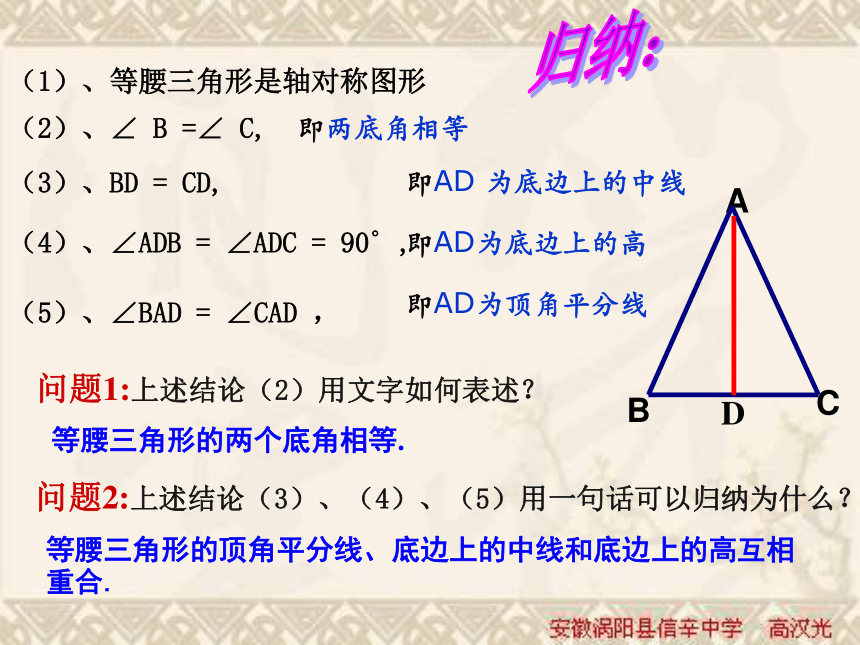
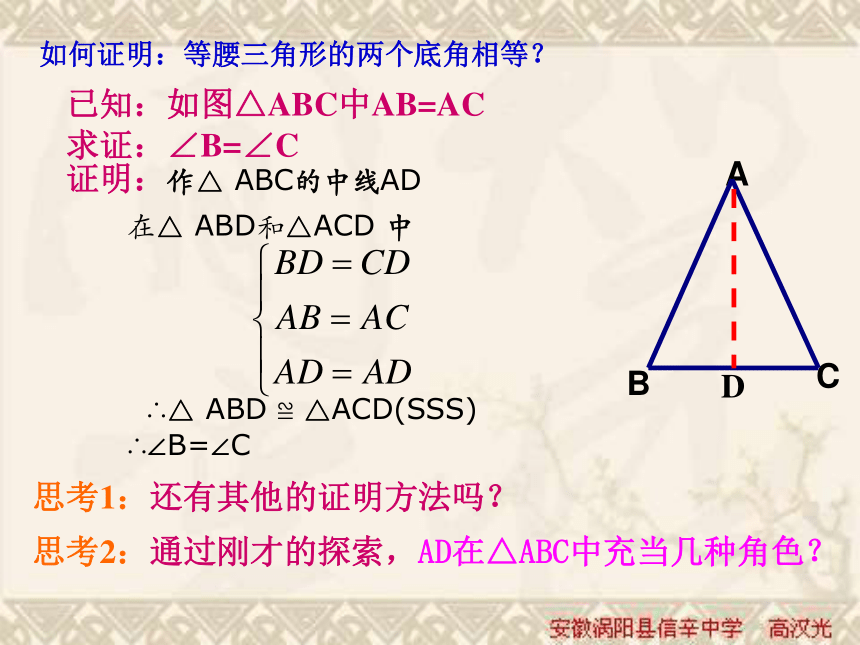
你能发现什么现象呢?二.等腰三角形性质的探索BACD 通过折叠你发现图形中有哪些相等的线段或角?(1)、等腰三角形是轴对称图形(2)、∠ B =∠ C,(3)、BD = CD,(4)、∠ADB = ∠ADC = 90°,(5)、∠BAD = ∠CAD ,问题1:上述结论(2)用文字如何表述?等腰三角形的两个底角相等.问题2:上述结论(3)、(4)、(5)用一句话可以归纳为什么?等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.归纳:即两底角相等即AD 为底边上的中线即AD为底边上的高即AD为顶角平分线D如何证明:等腰三角形的两个底角相等?已知:如图△ABC中AB=AC求证:∠B=∠C证明:作△ ABC的中线AD
在△ ABD和△ACD 中
∴△ ABD ≌ △ACD(SSS)
∴∠B=∠C思考1:还有其他的证明方法吗?思考2:通过刚才的探索,AD在△ABC中充当几种角色?等腰三角形的性质1、等腰三角形的两个底角相等
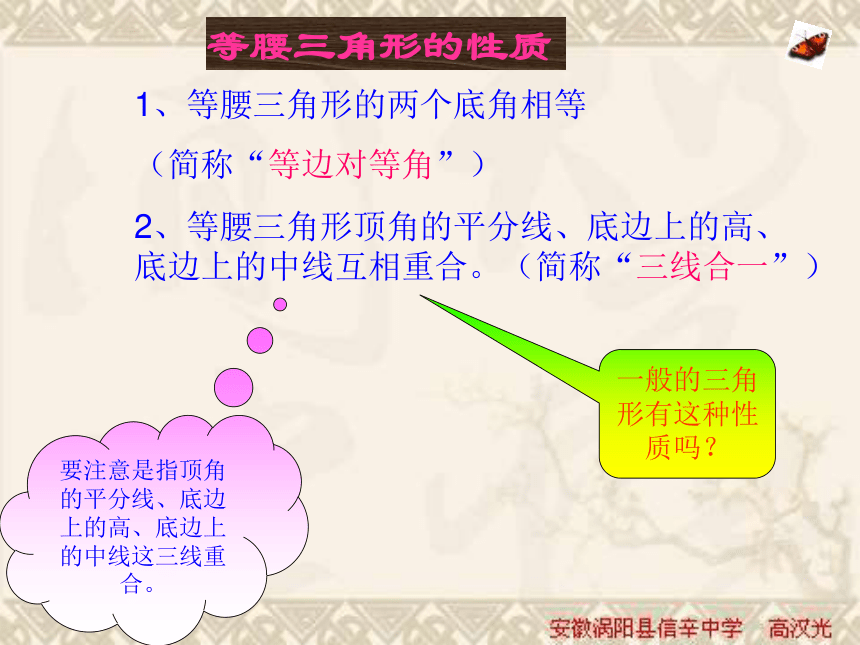
(简称“等边对等角”)2、等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合。(简称“三线合一”)一般的三角形有这种性质吗?要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。CDBA1、(1) 在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等边对等角① ∵AD⊥BC,
∴∠____ = ∠____,___= ___ ② ∵AD是中线,∴___⊥___ ,∠____ =∠____③∵AD是角平分线,
∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD(2) 在△ABC中, AB=AC时, 课堂练习:(三线合一)2 、在△ ABC中,若AB=BC=CA,
则 ∠A=______
∠B=______
∠C=______
推论:
等边三角形三个内角都相等,每一个角都等于 。课堂练习:60 °60 °60 °60°
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°
又∵BD=AD(已知)
∴∠BAD=∠B= 30°(等边对等角)
同理 ∠CAE =∠C= 30°
∴∠DAE =∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60 °例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,
求∠DAE的度数。能力拓展: 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟方法三:
证明△ ABE≌ △ ACD例2: 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720⒈等腰三角形一个底角为40°,它的顶角为______.⒉等腰三角形一顶角为40°,它的另外两个底角为
__________________.⒊等腰三角形一个角为40°,它的另外两个角为___________.100 °100°,40 °
或70 °,70 ° 70°,70° 4.等腰三角形一个角为120°,它的另外两个角为 . 30°30°1.如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC,试判断△ABC的形状,并说明理由? BDACE12作业:2.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?C3.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?ABCEDO4.如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,EG∥BC.请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCF5.如图,△ABC中,∠C=90°,AC=BC,AD是角平分线。求证:AB=AC+DC。ABCED6.如图:在△ABC中,AB=AC,∠1=∠2,求证:AD平分∠BAC。7、如图,已知AB=AC,EB=EC,
结论∠ABE= ∠ACE是否正确?
说明理由。8.已知如图,△ABC中,AB=AC,O是△ABC内一点,且OB=OC,AO的延长线交BC于D。 求证:AD⊥BC,BD=CD。挑战题: 1.已知,如图△ABC是等边三角形,AE平分∠BAC交BC于E,以BE为边向△ABC的外部作等边△BED。
求证:BD⊥CD
2.已知:如图,△ABC中,AB=AC,D点在AB上,E点在AC的延长线上,且BD=CE,连结DE,交BC于F求证:DF=EF 3. 如图,已知∠ABC=20°,
BD=DE=EF=FG。 (1)∠ABC内符合条件BD=DE=EF=FG的折线
(如BD、DE、EF)共有几条?
(2) 若∠ABC= 10°呢?试一试,并说明理由。小结:1、等腰三角形的性质:等边对等角2、 等腰三角形顶角的平分线垂直平分底边(三线合一)本节课你学到了什么? 4、有时利用等腰三角形的“三线合一”性质作辅助线(顶角的平分线、底边上的高、底边上的中线),可帮助我们解决实际问题。3、等边三角形三个内角相等,每一个内角都等于60°
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?二.等腰三角形性质的探索BACD 通过折叠你发现图形中有哪些相等的线段或角?(1)、等腰三角形是轴对称图形(2)、∠ B =∠ C,(3)、BD = CD,(4)、∠ADB = ∠ADC = 90°,(5)、∠BAD = ∠CAD ,问题1:上述结论(2)用文字如何表述?等腰三角形的两个底角相等.问题2:上述结论(3)、(4)、(5)用一句话可以归纳为什么?等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.归纳:即两底角相等即AD 为底边上的中线即AD为底边上的高即AD为顶角平分线D如何证明:等腰三角形的两个底角相等?已知:如图△ABC中AB=AC求证:∠B=∠C证明:作△ ABC的中线AD
在△ ABD和△ACD 中
∴△ ABD ≌ △ACD(SSS)
∴∠B=∠C思考1:还有其他的证明方法吗?思考2:通过刚才的探索,AD在△ABC中充当几种角色?等腰三角形的性质1、等腰三角形的两个底角相等
(简称“等边对等角”)2、等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合。(简称“三线合一”)一般的三角形有这种性质吗?要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。CDBA1、(1) 在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等边对等角① ∵AD⊥BC,
∴∠____ = ∠____,___= ___ ② ∵AD是中线,∴___⊥___ ,∠____ =∠____③∵AD是角平分线,
∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD(2) 在△ABC中, AB=AC时, 课堂练习:(三线合一)2 、在△ ABC中,若AB=BC=CA,
则 ∠A=______
∠B=______
∠C=______
推论:
等边三角形三个内角都相等,每一个角都等于 。课堂练习:60 °60 °60 °60°
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°
又∵BD=AD(已知)
∴∠BAD=∠B= 30°(等边对等角)
同理 ∠CAE =∠C= 30°
∴∠DAE =∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60 °例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,
求∠DAE的度数。能力拓展: 已知,如图AB=AC,AD=AE。求证:BD=CE。EDCBA方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF∟方法三:
证明△ ABE≌ △ ACD例2: 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=∠C=∠BDC
∠A=∠ABD (等边对等角)设∠A=x,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有
∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720⒈等腰三角形一个底角为40°,它的顶角为______.⒉等腰三角形一顶角为40°,它的另外两个底角为
__________________.⒊等腰三角形一个角为40°,它的另外两个角为___________.100 °100°,40 °
或70 °,70 ° 70°,70° 4.等腰三角形一个角为120°,它的另外两个角为 . 30°30°1.如图,AD是△ABC的外角∠EAC的平分线,且AD∥BC,试判断△ABC的形状,并说明理由? BDACE12作业:2.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?C3.如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于点O,那么△OBC是什么三角形?为什么?ABCEDO4.如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,EG∥BC.请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCF5.如图,△ABC中,∠C=90°,AC=BC,AD是角平分线。求证:AB=AC+DC。ABCED6.如图:在△ABC中,AB=AC,∠1=∠2,求证:AD平分∠BAC。7、如图,已知AB=AC,EB=EC,
结论∠ABE= ∠ACE是否正确?
说明理由。8.已知如图,△ABC中,AB=AC,O是△ABC内一点,且OB=OC,AO的延长线交BC于D。 求证:AD⊥BC,BD=CD。挑战题: 1.已知,如图△ABC是等边三角形,AE平分∠BAC交BC于E,以BE为边向△ABC的外部作等边△BED。
求证:BD⊥CD
2.已知:如图,△ABC中,AB=AC,D点在AB上,E点在AC的延长线上,且BD=CE,连结DE,交BC于F求证:DF=EF 3. 如图,已知∠ABC=20°,
BD=DE=EF=FG。 (1)∠ABC内符合条件BD=DE=EF=FG的折线
(如BD、DE、EF)共有几条?
(2) 若∠ABC= 10°呢?试一试,并说明理由。小结:1、等腰三角形的性质:等边对等角2、 等腰三角形顶角的平分线垂直平分底边(三线合一)本节课你学到了什么? 4、有时利用等腰三角形的“三线合一”性质作辅助线(顶角的平分线、底边上的高、底边上的中线),可帮助我们解决实际问题。3、等边三角形三个内角相等,每一个内角都等于60°
