沪科版数学八上16.3等腰三角形的判定
文档属性
| 名称 | 沪科版数学八上16.3等腰三角形的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 360.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-15 20:49:14 | ||
图片预览








文档简介
课件25张PPT。1.等腰三角形的两腰相等;2.等腰三角形的两个底角相等,(简称“在同一个三角形中,等边对等角”)
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合(简称“等腰三角形三线合一”)4.等腰三角形是轴对称图形,对称轴是底边的中垂线。1.如图:ΔABC中,已知AB=AC,∠ B= ∠ C(在同一个三角形中,等边对等角).2、反过来:在ΔABC中,∠ B= ∠ C, AB=AC成立吗?已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边
相等)12已知在一个三角形中,等角对等边 定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB. ( )用符号语言表示为:这又是一个判定两条线段相等根据之一.
推论1:证明已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
推论1.三个角都相等的三角形是等边三角形 安徽省涡阳县信辛中学 高汉光推论2:证明问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?第一种情况:当顶角是600时。
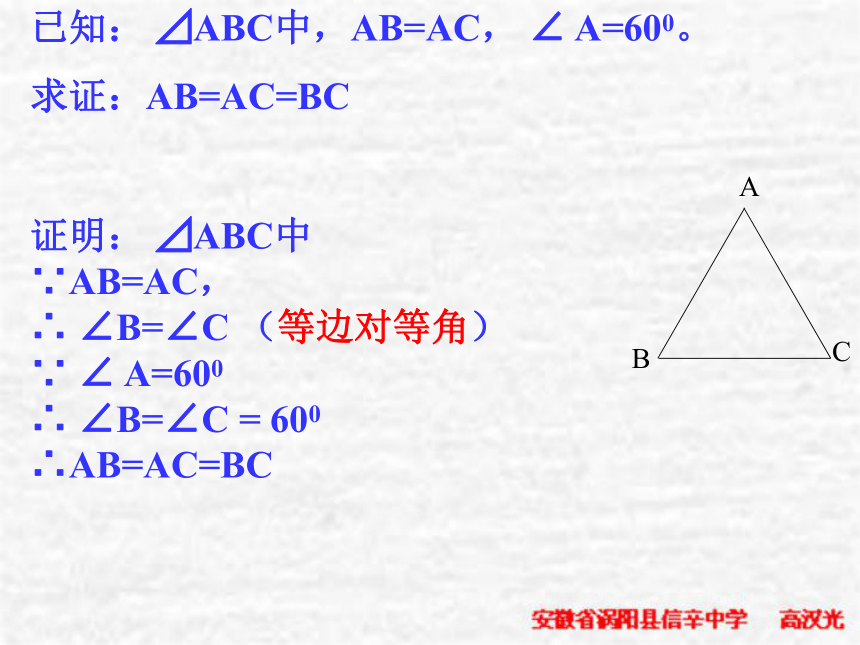
第二种情况:当底角是600时。已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
推论2.
有一个角是600的等腰三角形是等边三角形 如图:△ABC是直角三角形,其中,∠C=90°∠A=30°,若延长BC到点D,使BC=DC,则△ABD是等边三角形。则AB=BD=AD=1/2BC。 ABDC30°推论3 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
300 问:如图,下列推理正确吗? (等角对等边)(等角对等边)错,因为都不是在同一个三角形中。解: ∵ ∠ DAC= ∠ ACB+ ∠ ABC
(三角形外角的性质)∴ ∠ ABC= ∠ DAC -∠ ACB
=60 °- 30 ° =30 °∵ ∠ ABC= ∠ ACB∴ AB=AC(在同一个三角形中, 等角对等边)即AC的长就是河宽。 范例讲解:例1:一次数学实践活动的内容是测量河宽,如图,即测量A, B之间的距离。小明想出了一个方法:从点A出发,沿着与直线AB成60 °角的AC方向前进至C , 在C处测得∠ C= 30 °,量出AC的长,它就是河的宽度。这个方法正确吗?请说明理由。想一想:还有其它测量河宽的方法吗?ABCED例2:已知,如图等边△AEB与等 边△BCD在线段AC的同侧 求证: △ABD≌△EBCA B C DE变式:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
例3:如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)例4: 已知:如图,∠A=90°,∠B=15°,BD=DC. 求证:AC= BD.证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD例5:如图,在等边△ABC中,AF=BD=CE, 求证:△DEF也是等边三角形.证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
1.已知:如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长 2.上午8时,一条船从A处出发以15海里/小时的速度向北航行,10时到达B处,从A,B望灯塔C,测的∠NAC=42°,∠NBC=84°求从B处到灯塔C的距离。
CBA N 北南84°42°3.如图是屋架设计图的一部分,其中BC⊥AC,DE⊥AC,点D是AB的中点,∠A=30°,AB=7.4m,求BC,DE的长。
?
BACDE30°4.如图,△ABC中,∠C=90°,AC=BC,AD是角平分线。求证:AB=AC+DC。ABCED5.如图:在△ABC中,AB=AC,∠1=∠2,
求证:AD平分∠BAC。ABCDM12有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.2.等角对等边,1.两边相等。1.两腰相等.
3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合(简称“等腰三角形三线合一”)4.等腰三角形是轴对称图形,对称轴是底边的中垂线。1.如图:ΔABC中,已知AB=AC,∠ B= ∠ C(在同一个三角形中,等边对等角).2、反过来:在ΔABC中,∠ B= ∠ C, AB=AC成立吗?已知:⊿ABC中,∠B=∠C求证:AB=AC证明:作∠BAC的平分线AD在⊿BAD和⊿CAD中,∠1=∠2,
∠B=∠C,
AD=AD∴ ⊿BAD≌ ⊿CAD(AAS)∴AB=AC(全等三角形的对应边
相等)12已知在一个三角形中,等角对等边 定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB. ( )用符号语言表示为:这又是一个判定两条线段相等根据之一.
推论1:证明已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
推论1.三个角都相等的三角形是等边三角形 安徽省涡阳县信辛中学 高汉光推论2:证明问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?第一种情况:当顶角是600时。
第二种情况:当底角是600时。已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC
已知: ⊿ABC中,AB=AC, ∠B=600。
求证:AB=AC=BC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=600
∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
推论2.
有一个角是600的等腰三角形是等边三角形 如图:△ABC是直角三角形,其中,∠C=90°∠A=30°,若延长BC到点D,使BC=DC,则△ABD是等边三角形。则AB=BD=AD=1/2BC。 ABDC30°推论3 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
300 问:如图,下列推理正确吗? (等角对等边)(等角对等边)错,因为都不是在同一个三角形中。解: ∵ ∠ DAC= ∠ ACB+ ∠ ABC
(三角形外角的性质)∴ ∠ ABC= ∠ DAC -∠ ACB
=60 °- 30 ° =30 °∵ ∠ ABC= ∠ ACB∴ AB=AC(在同一个三角形中, 等角对等边)即AC的长就是河宽。 范例讲解:例1:一次数学实践活动的内容是测量河宽,如图,即测量A, B之间的距离。小明想出了一个方法:从点A出发,沿着与直线AB成60 °角的AC方向前进至C , 在C处测得∠ C= 30 °,量出AC的长,它就是河的宽度。这个方法正确吗?请说明理由。想一想:还有其它测量河宽的方法吗?ABCED例2:已知,如图等边△AEB与等 边△BCD在线段AC的同侧 求证: △ABD≌△EBCA B C DE变式:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
例3:如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)例4: 已知:如图,∠A=90°,∠B=15°,BD=DC. 求证:AC= BD.证明:
∵BD=DC,∠B=15°
∴∠DCB=∠B=15°(等角对等边)
∴∠ADC=∠B+∠DCB=30°
(三角形的外角等于和它不相邻的两个内角的和)
∵∠A=90°
∴AC= DC
∴AC= BD例5:如图,在等边△ABC中,AF=BD=CE, 求证:△DEF也是等边三角形.证明:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BD=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
1.已知:如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长 2.上午8时,一条船从A处出发以15海里/小时的速度向北航行,10时到达B处,从A,B望灯塔C,测的∠NAC=42°,∠NBC=84°求从B处到灯塔C的距离。
CBA N 北南84°42°3.如图是屋架设计图的一部分,其中BC⊥AC,DE⊥AC,点D是AB的中点,∠A=30°,AB=7.4m,求BC,DE的长。
?
BACDE30°4.如图,△ABC中,∠C=90°,AC=BC,AD是角平分线。求证:AB=AC+DC。ABCED5.如图:在△ABC中,AB=AC,∠1=∠2,
求证:AD平分∠BAC。ABCDM12有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.2.等角对等边,1.两边相等。1.两腰相等.
