小学数学北师大版六年级下册 四 正比例与反比例 变化的变量 学案(表格式 含答案)
文档属性
| 名称 | 小学数学北师大版六年级下册 四 正比例与反比例 变化的变量 学案(表格式 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 126.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览

文档简介
课题 正比例与反比例-变化的变量学案
知识点 变化的变量。生活中存在着大量互相关联的变量,在一定条件下变量之间的变化还存在着一定的规律,可以通过表格或图像表示出来。
案例 原题 星期天,王刚乘车去游乐场游玩。出租车的票价如下图。请根据下图,说一说票价是如何随里程的变化而变化的。
解析 票价在4千米以内(包括4千米)无变化,超过4千米,票价随里程的变化而变化,也就是里程每增加1千米,票价增加1.5元。
点拔 本题容易错在学生未能注意到前4千米票价并未随着路程的变化而变化,直接回答成“票价随里程的增加而增加。
归纳 在理解两个量之间的变化关系时,一定要注意,有时候两个量之间并不总是有着同一个变化关系,而只是在某一段范围内存在着一种变化关系。
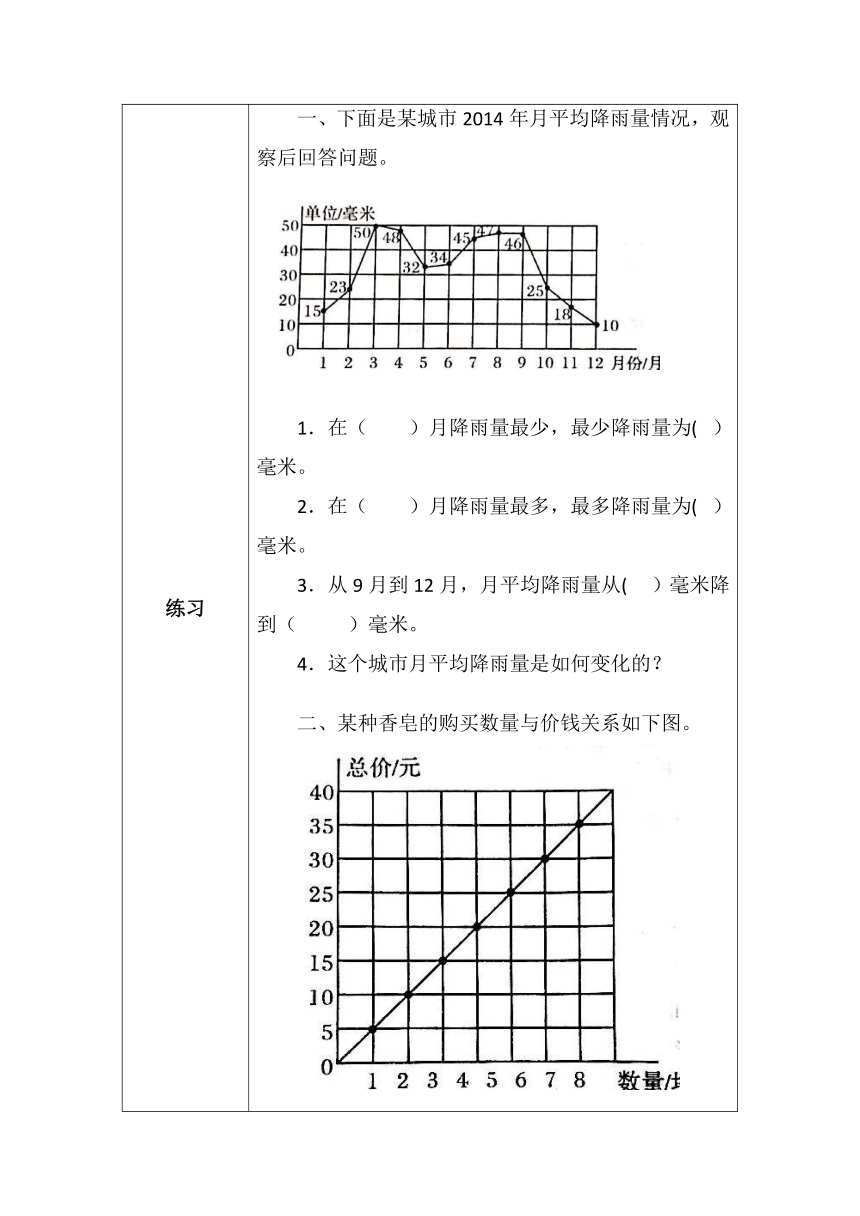
练习 一、下面是某城市2014年月平均降雨量情况,观察后回答问题。 1.在( )月降雨量最少,最少降雨量为( )毫米。 2.在( )月降雨量最多,最多降雨量为( )毫米。 3.从9月到12月,月平均降雨量从( )毫米降到( )毫米。 4.这个城市月平均降雨量是如何变化的? 二、某种香皂的购买数量与价钱关系如下图。 1.上图中有哪些量在变化? 2.香皂的总价与数量是如何变化的?
答案 练习 一、1. 12 10 3 50 46 10 4.这个城市月平均降雨量在1~3月逐月上升,3~5月逐月下降,5~8月缓慢上升,8~12月呈下降趋势。 二、1.图中香皂的数量和总价在变化。 2.购买香皂的数量增加了,总价也随之增加。购买香皂的块数量越多,总价就越多。
教材 【教材第40页“练一练”】 1.圆柱的体积随圆柱高的增加而增加。 2.(1)18米 3米(2)0~6分 6~12分(3)12分 3.t=n÷7+3
存在问 题摘要 (1). ; (2). ; (3). 。
反思 变化的量这部分内容,主要是让学生初步体会、理解函数思想,认识变化量之间的关系,让学生经历相关联的量的多种表示方法,如表格表示法、图像表示法等。为此,教材设置了“妙想6周岁前体重变化情况表和图”“骆驼体温变化统计图”等情境,让学生在观察这些情境的基础上,思考、讨论、交流,从而感受到生活中存在着许多相联的变量。教师在教学中,首先要让学生弄清题意,看懂图表,然后根据图表等所要表达的信息,回答问题,并尝试用自己的语言描述题中变量之间的关系;也可以引导学生举出生活中一个量随另一个量的变化而变化的例子,只要学生说的合理,就要给予肯定。
课外资料 根据量的变化关系巧测树高 一天,六(3)班的同学在李老师的带领下到野外去郊游。玩累了,大家一起坐在一棵大树下休息。此时李老师对同学们说:“我们身旁的这棵大树很高,大家能用我们学过的知识,想办法测量出这棵大树的高度吗?”同学们七嘴八舌地议论起来。 一会儿,数学课代表李梅说:“我有办法了。”说着,她捡起一根树枝,对大家说:“这根树枝大约1米长,把它立在地上,可以目测出它的影长大约是0.4米,我再用步测出大树的影子大约是4米,这样就可以计算出大树的高度了。”聪明的小朋友,你知识该如何计算出大树的高度吗?
知识点 变化的变量。生活中存在着大量互相关联的变量,在一定条件下变量之间的变化还存在着一定的规律,可以通过表格或图像表示出来。
案例 原题 星期天,王刚乘车去游乐场游玩。出租车的票价如下图。请根据下图,说一说票价是如何随里程的变化而变化的。
解析 票价在4千米以内(包括4千米)无变化,超过4千米,票价随里程的变化而变化,也就是里程每增加1千米,票价增加1.5元。
点拔 本题容易错在学生未能注意到前4千米票价并未随着路程的变化而变化,直接回答成“票价随里程的增加而增加。
归纳 在理解两个量之间的变化关系时,一定要注意,有时候两个量之间并不总是有着同一个变化关系,而只是在某一段范围内存在着一种变化关系。
练习 一、下面是某城市2014年月平均降雨量情况,观察后回答问题。 1.在( )月降雨量最少,最少降雨量为( )毫米。 2.在( )月降雨量最多,最多降雨量为( )毫米。 3.从9月到12月,月平均降雨量从( )毫米降到( )毫米。 4.这个城市月平均降雨量是如何变化的? 二、某种香皂的购买数量与价钱关系如下图。 1.上图中有哪些量在变化? 2.香皂的总价与数量是如何变化的?
答案 练习 一、1. 12 10 3 50 46 10 4.这个城市月平均降雨量在1~3月逐月上升,3~5月逐月下降,5~8月缓慢上升,8~12月呈下降趋势。 二、1.图中香皂的数量和总价在变化。 2.购买香皂的数量增加了,总价也随之增加。购买香皂的块数量越多,总价就越多。
教材 【教材第40页“练一练”】 1.圆柱的体积随圆柱高的增加而增加。 2.(1)18米 3米(2)0~6分 6~12分(3)12分 3.t=n÷7+3
存在问 题摘要 (1). ; (2). ; (3). 。
反思 变化的量这部分内容,主要是让学生初步体会、理解函数思想,认识变化量之间的关系,让学生经历相关联的量的多种表示方法,如表格表示法、图像表示法等。为此,教材设置了“妙想6周岁前体重变化情况表和图”“骆驼体温变化统计图”等情境,让学生在观察这些情境的基础上,思考、讨论、交流,从而感受到生活中存在着许多相联的变量。教师在教学中,首先要让学生弄清题意,看懂图表,然后根据图表等所要表达的信息,回答问题,并尝试用自己的语言描述题中变量之间的关系;也可以引导学生举出生活中一个量随另一个量的变化而变化的例子,只要学生说的合理,就要给予肯定。
课外资料 根据量的变化关系巧测树高 一天,六(3)班的同学在李老师的带领下到野外去郊游。玩累了,大家一起坐在一棵大树下休息。此时李老师对同学们说:“我们身旁的这棵大树很高,大家能用我们学过的知识,想办法测量出这棵大树的高度吗?”同学们七嘴八舌地议论起来。 一会儿,数学课代表李梅说:“我有办法了。”说着,她捡起一根树枝,对大家说:“这根树枝大约1米长,把它立在地上,可以目测出它的影长大约是0.4米,我再用步测出大树的影子大约是4米,这样就可以计算出大树的高度了。”聪明的小朋友,你知识该如何计算出大树的高度吗?
