小学数学 北师大版 六年级下册 四 正比例与反比例 画一画 学案(表格式 含答案)
文档属性
| 名称 | 小学数学 北师大版 六年级下册 四 正比例与反比例 画一画 学案(表格式 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 151.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 14:05:50 | ||
图片预览

文档简介
课题 正比例与反比例-画一画学案
知识点 认识正比例图像。 绘制正比例图像时,首先根据题中相关联的两个变量所对应的数据在图中描出各个点,然后把这些点顺次连接起来,就可以发现正比例的图像是一条直线。
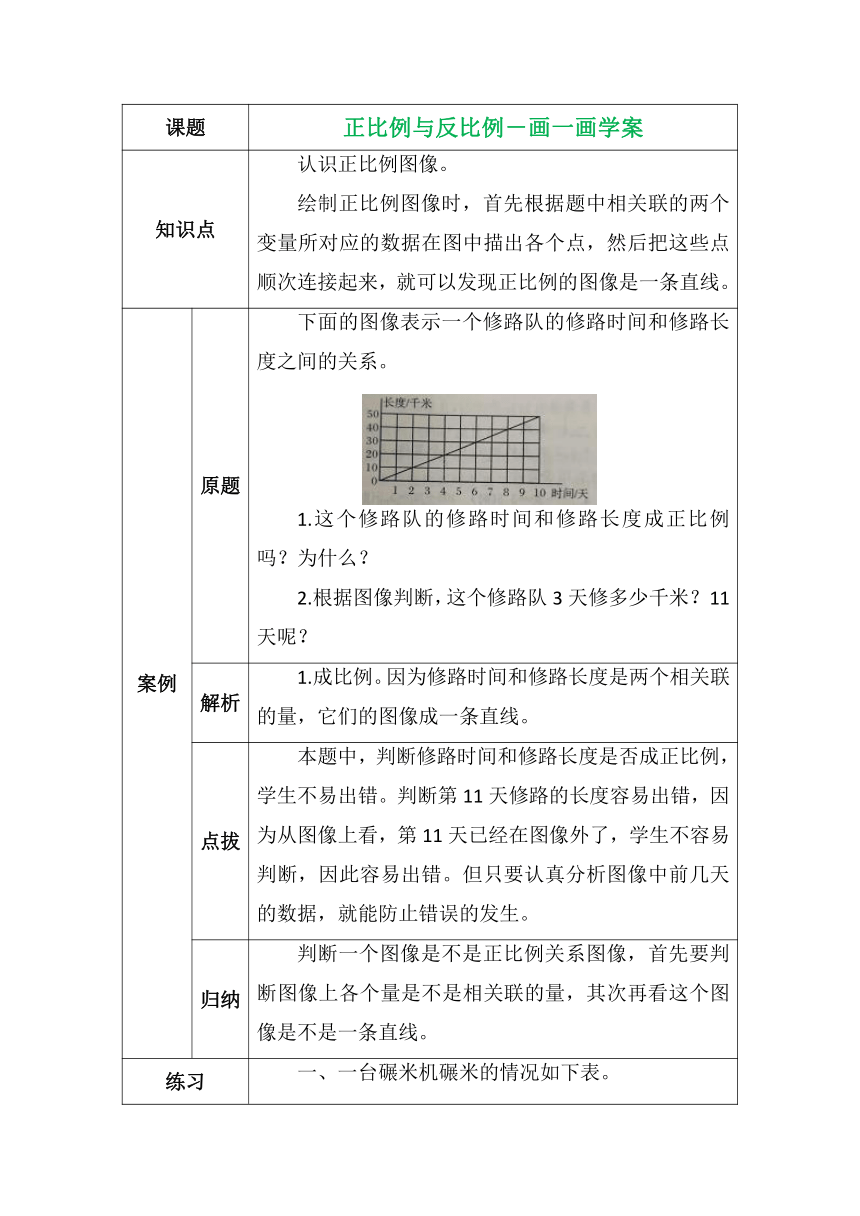
案例 原题 下面的图像表示一个修路队的修路时间和修路长度之间的关系。 1.这个修路队的修路时间和修路长度成正比例吗?为什么? 2.根据图像判断,这个修路队3天修多少千米?11天呢?
解析 1.成比例。因为修路时间和修路长度是两个相关联的量,它们的图像成一条直线。
点拔 本题中,判断修路时间和修路长度是否成正比例,学生不易出错。判断第11天修路的长度容易出错,因为从图像上看,第11天已经在图像外了,学生不容易判断,因此容易出错。但只要认真分析图像中前几天的数据,就能防止错误的发生。
归纳 判断一个图像是不是正比例关系图像,首先要判断图像上各个量是不是相关联的量,其次再看这个图像是不是一条直线。
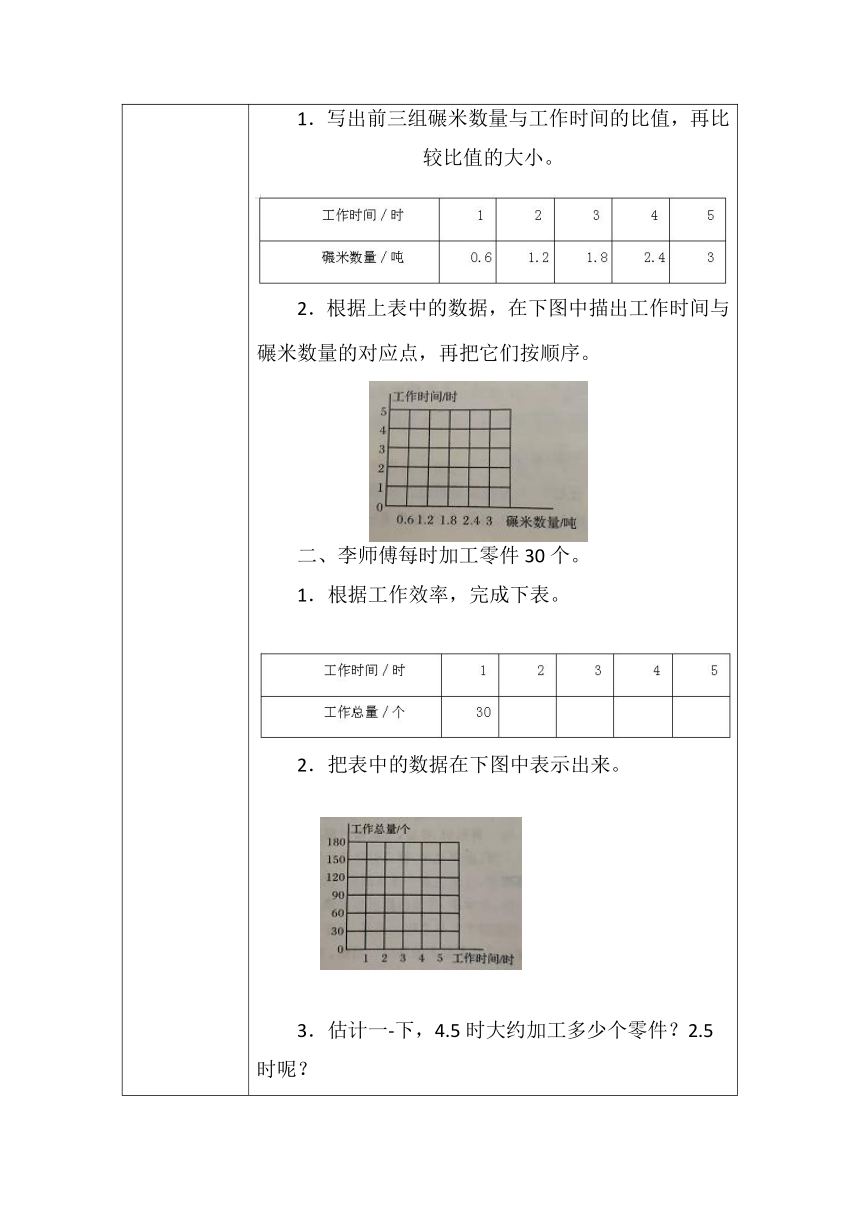
练习 一、一台碾米机碾米的情况如下表。 1.写出前三组碾米数量与工作时间的比值,再比较比值的大小。 2.根据上表中的数据,在下图中描出工作时间与碾米数量的对应点,再把它们按顺序。 二、李师傅每时加工零件30个。 1.根据工作效率,完成下表。 2.把表中的数据在下图中表示出来。 3.估计一-下,4.5时大约加工多少个零件?2.5时呢? 4.如果加工165个零件需要几时?105个零件呢?
答案 练习 一、1.=0.6 =0.6 =0.6 = = =0.6 2.略 二、1~2.略 3.4.5时大约加工135个零件,2.5时大约加工75个零件。1 4.165÷30=5.5(时)105÷30=3.5(时)
教材 【教材第45页“练一练”】 (1)20 25 30 35 (2)成正比例 (3)发现连接各点后,图像是一条直线。 (4)在直线上,这一点表示8个人需要船费40元。 2.成正比例,因为在弹性限度内,弹簧伸长的长度与物体重量的比值是一定的。
存在问 题摘要 (1). ; (2). ; (3). 。
反思 画一画这一内容是在学生学习了变化的量和正比例这两节内容后安排的,通过前面两节内容的学习,学生已经认识到生活中存在着许多相互依存的变量,懂得了正比例的意义,能初步判断两个相关联的量是否成正比例。在此基础上,本节课旨在让学生初步认识正比例图像。本节课教材设置了看电影的问题情境,首先通过判断看电影的人数和所付票费之间是否成正比例关系,让学生进一步认识正比例,以及正比例中两个相关联的量之间的关系;然后再让学生根据表中的数据在方格纸上描出成正比例的量所对应的点,并用线连成正比例图像;最后让学生通过观察,了解正比例图像的特点,并能根据图像中一个变量的值估计所对应的变量的值。教师在教学中要注意引导学生运用已有的知识,在观察中发现正比例图像可形成一条直线的特点。另外,学生在用描点法画正比例图像时,教师要注意引导学生数清格数,正确描出点的位置。
课外资料 正比例关系图像是否经过原点一般来说,正比例关系的图像是一条经过原点(0,0)的直线,它的画法和折线统计图的画法相同。从图像中,可以直观地看到两种量的变化情况,还可以由一个量的值直接找到对应的另一个量的值。因为正比例关系中,两个变量的比值是一定的。有人认为,比表示两个数相除,而0不能作除数,所以正比例图像不能从原点(0,0)画起。而且,正比例图像的那条直线的一端如果正好到从0开始,这样就非常容易会让学生误认为正比例的图像其实就是一条射线,所以这些人认为在小学正比例的图像的那条直线,可以不画到0,画到0反而不好。但是在现实生活中,有0的情况是大量存在的,所以,正比例关系图像是一条经过原点的直线,那么正比例与其道理相同,正比例反映的是两个量之间相互变化的关系,用正比例图像反应出来变化的趋势更加明显,是一条直线。关于原点到第一个数据这一段的处理,应该描出来,它同样反应了两个量的变化关系。
知识点 认识正比例图像。 绘制正比例图像时,首先根据题中相关联的两个变量所对应的数据在图中描出各个点,然后把这些点顺次连接起来,就可以发现正比例的图像是一条直线。
案例 原题 下面的图像表示一个修路队的修路时间和修路长度之间的关系。 1.这个修路队的修路时间和修路长度成正比例吗?为什么? 2.根据图像判断,这个修路队3天修多少千米?11天呢?
解析 1.成比例。因为修路时间和修路长度是两个相关联的量,它们的图像成一条直线。
点拔 本题中,判断修路时间和修路长度是否成正比例,学生不易出错。判断第11天修路的长度容易出错,因为从图像上看,第11天已经在图像外了,学生不容易判断,因此容易出错。但只要认真分析图像中前几天的数据,就能防止错误的发生。
归纳 判断一个图像是不是正比例关系图像,首先要判断图像上各个量是不是相关联的量,其次再看这个图像是不是一条直线。
练习 一、一台碾米机碾米的情况如下表。 1.写出前三组碾米数量与工作时间的比值,再比较比值的大小。 2.根据上表中的数据,在下图中描出工作时间与碾米数量的对应点,再把它们按顺序。 二、李师傅每时加工零件30个。 1.根据工作效率,完成下表。 2.把表中的数据在下图中表示出来。 3.估计一-下,4.5时大约加工多少个零件?2.5时呢? 4.如果加工165个零件需要几时?105个零件呢?
答案 练习 一、1.=0.6 =0.6 =0.6 = = =0.6 2.略 二、1~2.略 3.4.5时大约加工135个零件,2.5时大约加工75个零件。1 4.165÷30=5.5(时)105÷30=3.5(时)
教材 【教材第45页“练一练”】 (1)20 25 30 35 (2)成正比例 (3)发现连接各点后,图像是一条直线。 (4)在直线上,这一点表示8个人需要船费40元。 2.成正比例,因为在弹性限度内,弹簧伸长的长度与物体重量的比值是一定的。
存在问 题摘要 (1). ; (2). ; (3). 。
反思 画一画这一内容是在学生学习了变化的量和正比例这两节内容后安排的,通过前面两节内容的学习,学生已经认识到生活中存在着许多相互依存的变量,懂得了正比例的意义,能初步判断两个相关联的量是否成正比例。在此基础上,本节课旨在让学生初步认识正比例图像。本节课教材设置了看电影的问题情境,首先通过判断看电影的人数和所付票费之间是否成正比例关系,让学生进一步认识正比例,以及正比例中两个相关联的量之间的关系;然后再让学生根据表中的数据在方格纸上描出成正比例的量所对应的点,并用线连成正比例图像;最后让学生通过观察,了解正比例图像的特点,并能根据图像中一个变量的值估计所对应的变量的值。教师在教学中要注意引导学生运用已有的知识,在观察中发现正比例图像可形成一条直线的特点。另外,学生在用描点法画正比例图像时,教师要注意引导学生数清格数,正确描出点的位置。
课外资料 正比例关系图像是否经过原点一般来说,正比例关系的图像是一条经过原点(0,0)的直线,它的画法和折线统计图的画法相同。从图像中,可以直观地看到两种量的变化情况,还可以由一个量的值直接找到对应的另一个量的值。因为正比例关系中,两个变量的比值是一定的。有人认为,比表示两个数相除,而0不能作除数,所以正比例图像不能从原点(0,0)画起。而且,正比例图像的那条直线的一端如果正好到从0开始,这样就非常容易会让学生误认为正比例的图像其实就是一条射线,所以这些人认为在小学正比例的图像的那条直线,可以不画到0,画到0反而不好。但是在现实生活中,有0的情况是大量存在的,所以,正比例关系图像是一条经过原点的直线,那么正比例与其道理相同,正比例反映的是两个量之间相互变化的关系,用正比例图像反应出来变化的趋势更加明显,是一条直线。关于原点到第一个数据这一段的处理,应该描出来,它同样反应了两个量的变化关系。
