24.3正多边形和圆

课件24张PPT。24.3正多边形和圆 第二十四章 圆
土台九年制学校 蔡帮均教学目标：知识与技能：了解正多边形和圆的有关概念；理解并掌握正多边形半径、中心角、弦心距、边长之间的关系
过程与方法： ，会应用多边形和圆的有关知识解决实际问题． ．
情感态度与价值观: 复习正多边形概念，让学生尽可能讲出生活中的多边形为引题引入正多边形和圆这一节间的内容．
重点：讲清正多边形和圆中心正多边形半径、中心角、弦心距、边长之间的关系．
难点：通过例题使学生理解四者：正多边形半径、中心角、弦心距、边长之间的关系．
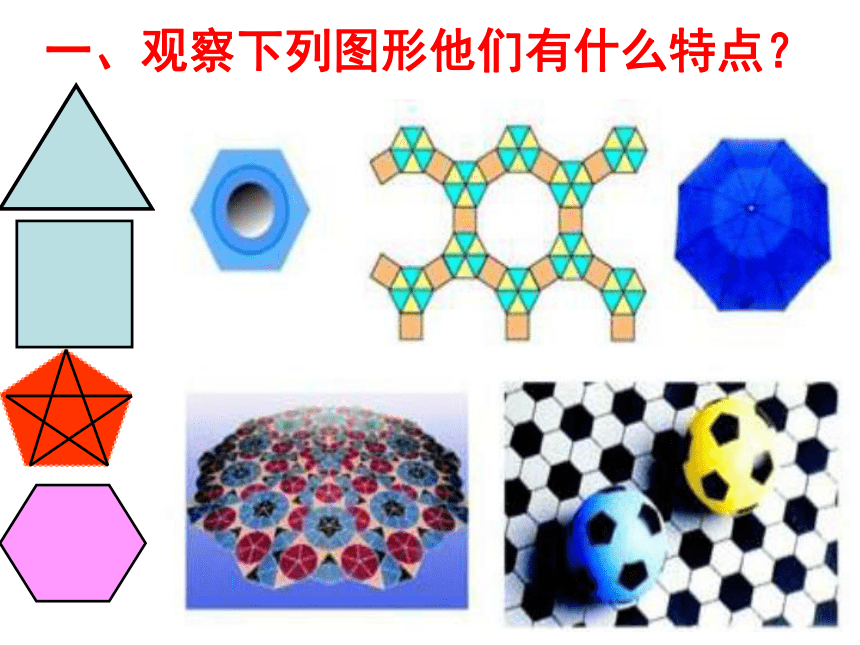
教学方法： 观察 发现 分析 归纳 讨论 练习一、观察下列图形他们有什么特点？二、小组合作 解读教材自学课本104页—105页内容
动手尝试，并要求讲出画图的方法？问题1：给你一个圆，你能把这个圆周四等分吗？问题2：你能把一个圆周五等分吗？请说出你的画
法。归纳：要把一个圆周进行等分，只要把圆心角进
行等分就可以了。一般地，要把一个圆周n等分，
只要把周角n等分即可，每一个圆心角的度数是
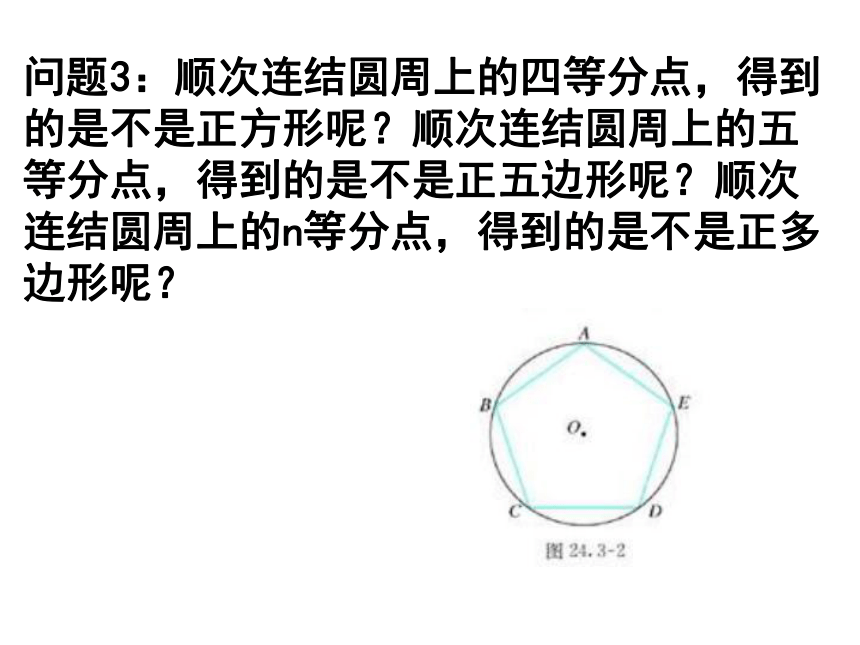
。问题3：顺次连结圆周上的四等分点，得到
的是不是正方形呢？顺次连结圆周上的五
等分点，得到的是不是正五边形呢？顺次
连结圆周上的n等分点，得到的是不是正多
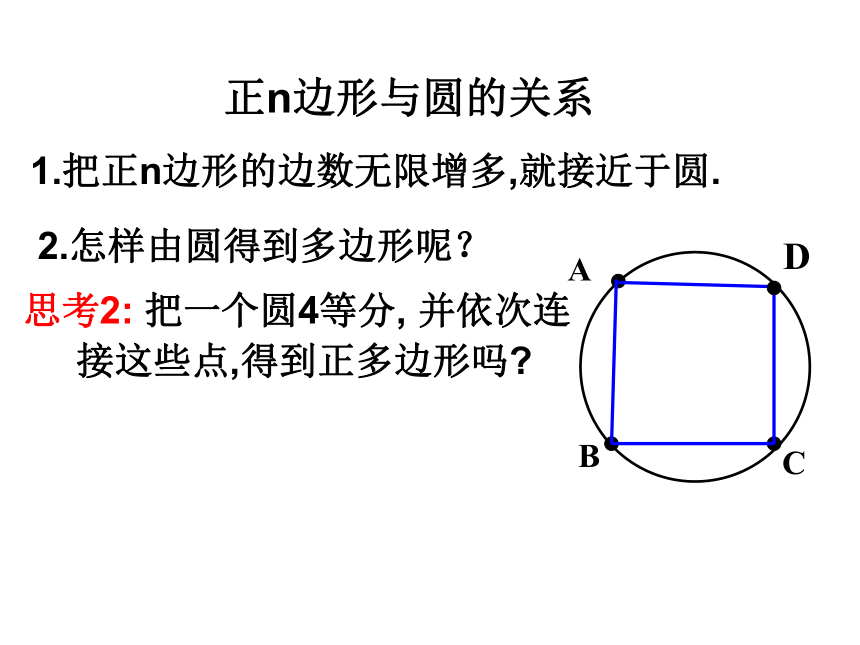
边形呢？正n边形与圆的关系1.把正n边形的边数无限增多,就接近于圆.2.怎样由圆得到多边形呢？ABCD思考2: 把一个圆4等分, 并依次连
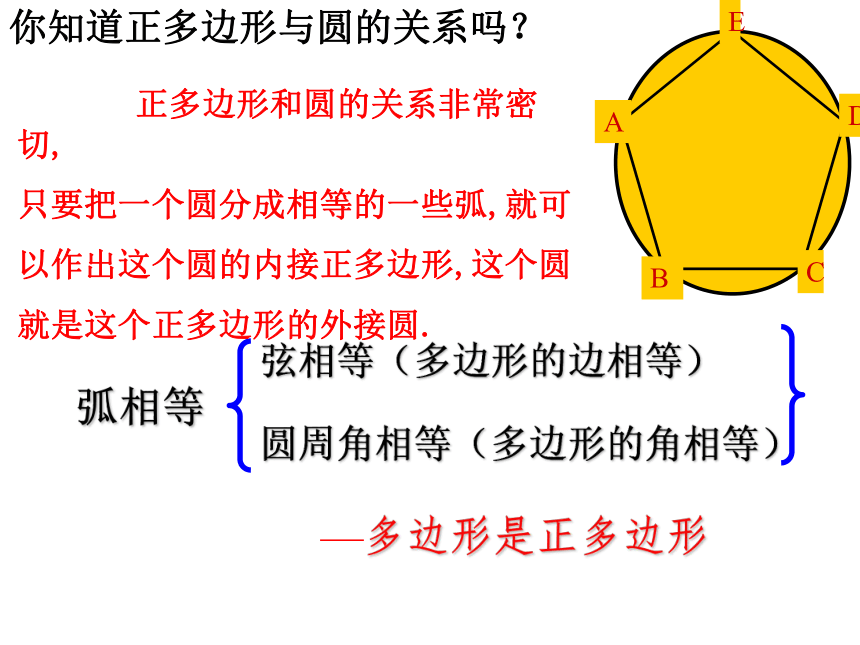
接这些点,得到正多边形吗?弧相等弦相等（多边形的边相等）圆周角相等（多边形的角相等）—多边形是正多边形你知道正多边形与圆的关系吗？ 正多边形和圆的关系非常密切,
只要把一个圆分成相等的一些弧,就可
以作出这个圆的内接正多边形,这个圆
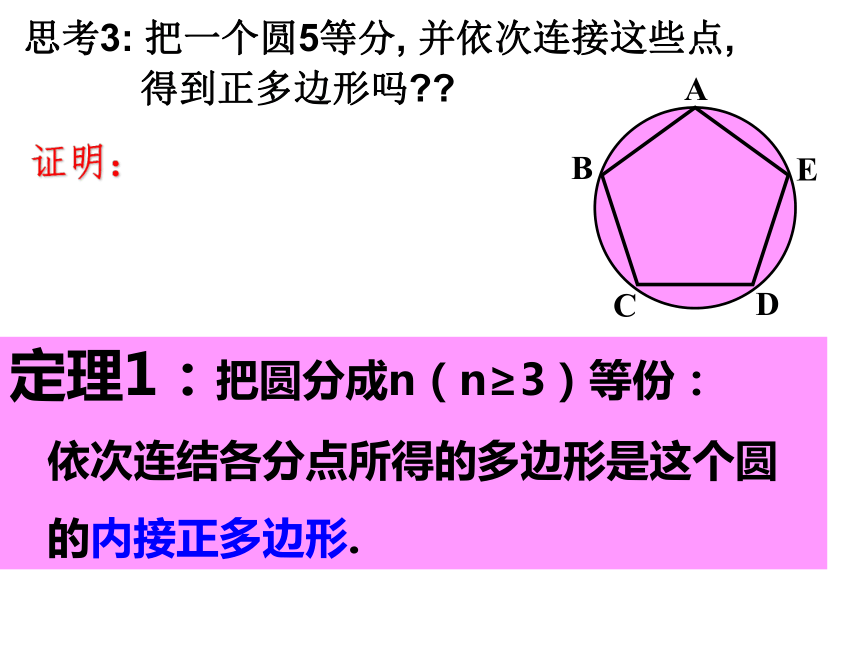
就是这个正多边形的外接圆.思考3: 把一个圆5等分, 并依次连接这些点,
得到正多边形吗??证明：ABCDE定理1：把圆分成n（n≥3）等份：
依次连结各分点所得的多边形是这个圆
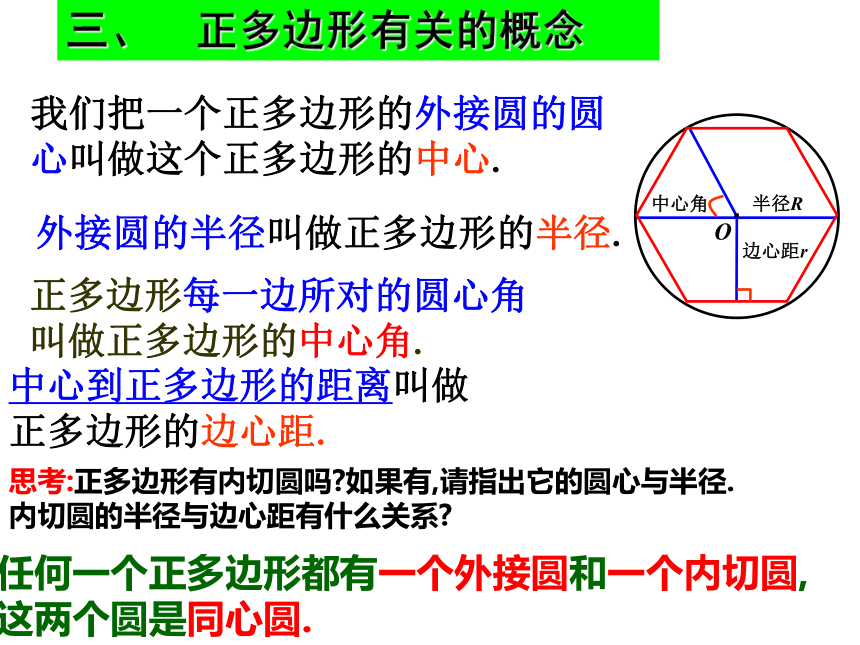
的内接正多边形.三、 正多边形有关的概念正多边形每一边所对的圆心角叫做正多边形的中心角.我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.思考:正多边形有内切圆吗?如果有,请指出它的圆心与半径.
内切圆的半径与边心距有什么关系? 任何一个正多边形都有一个外接圆和一个内切圆,
这两个圆是同心圆.1. O是正△ABC的中心，它是△ABC的_____
圆与________圆的圆心。2. OB叫正△ABC的_____,
它是正△ABC的______圆
的半径。 　　　　　3. OD叫作正△ABC______,
它是正△ABC的______
圆的半径。ABC　.OD外接内切半径外接边心距内切4. ∠BOC是正△ABC的________角; 中心∠BOC=_____度; ∠BOD=_____度.12060三、抢答题：5、正方形ABCD的外接圆圆心O叫做
正方形ABCD的____________6、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的___________ABCD.OE中心边心距7、⊙O是正五边形ABCDE的外接圆，弦AB的
弦心距OF叫正五边形ABCDE的________，
它是正五边形ABCDE的________圆的半径。8、∠AOB叫做正五边形ABCDE的_______角，
它的度数是________DEABC.OF边心距内切中心72度9、图中正六边形ABCDEF的中心角是_______;
它的度数是_________;10、你发现正六边形ABCDEF的半径与边长具有
什么数量关系？为什么？　BAEFCD.O∠AOB60度.O中心角ABG边心距把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,则周长为L=na.Ra正n边形的一个内角的度数是____________;
中心角的和是_____;正多边形一个中心角是___ _；
正N边形就有N个相等的中心角
正多边形的中心角与外角的大小关系是________.相等五例 有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积(精确到0.1平方米)..OBCrRP∴亭子的周长 L=6×4=24(m).OBCrR=4P四、练习1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不是正多边形，因为四条边不都相等;菱形不是正多边形，因为菱形的四个角不都相等;正方形是正多边形．因为四条边都相等，四个角都相等.解答：2、各边相等的圆内接多边形是正多边形吗？各角相等的圆内接多边形呢？如果是，说明理由，如果不是举出反例。 各边相等的圆内接多边形的各个角也相等，它是正多边形；各角相等的圆内接多边形不是正多边形，例如矩形。3、判断（1）各边都相等的正多边形是正多边形。（ ）
（2）一个圆有且只有一个内接正多形。（ ）××4.分别求出半径为R的圆内接正三角形，正方形的边长，边心距和面积.解：作等边△ABC的BC边上的高AD,垂足为D连接OB，则OB=R，BC=a在Rt△OBD中 ∠OBD=30°,边心距＝OD= BD=·ABCDOR即正三角形的边长为 边心距为 面积为 解：连接OB，OC 作OE⊥BC垂足为E，
∠OEB=90° ∠OBE= ∠ BOE=45°在Rt△OBE中为等腰直角三角形·ABCDOE 1、我的收获

2、我的疑惑 五、回顾与思考六、作业1、教材107页
　　　　第1、2题
2、完成<名师>相关部分作业。