苏教版数学五年级下册 六圆 单元综合练(word版 含解析)
文档属性
| 名称 | 苏教版数学五年级下册 六圆 单元综合练(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 117.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 14:30:33 | ||
图片预览

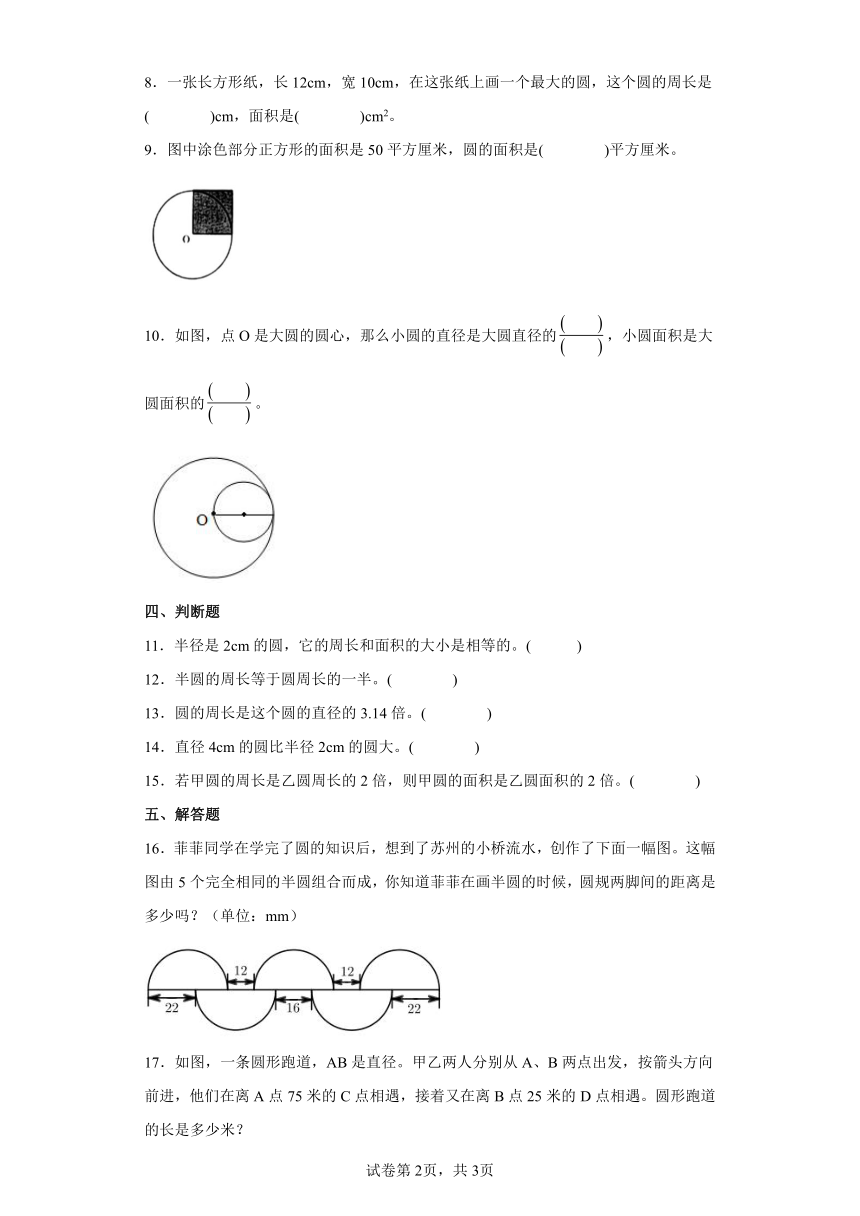


文档简介
苏教版五年级下册 六 圆 单元综合练
一、选择题
1.一个半圆,半径是r,它的周长是( )。
A. B. C.
2.甲圆的直径是乙圆的3倍,甲圆的面积是乙圆的( )倍。
A.9 B.6 C. D.3
3.下列说法,正确的有( )个。
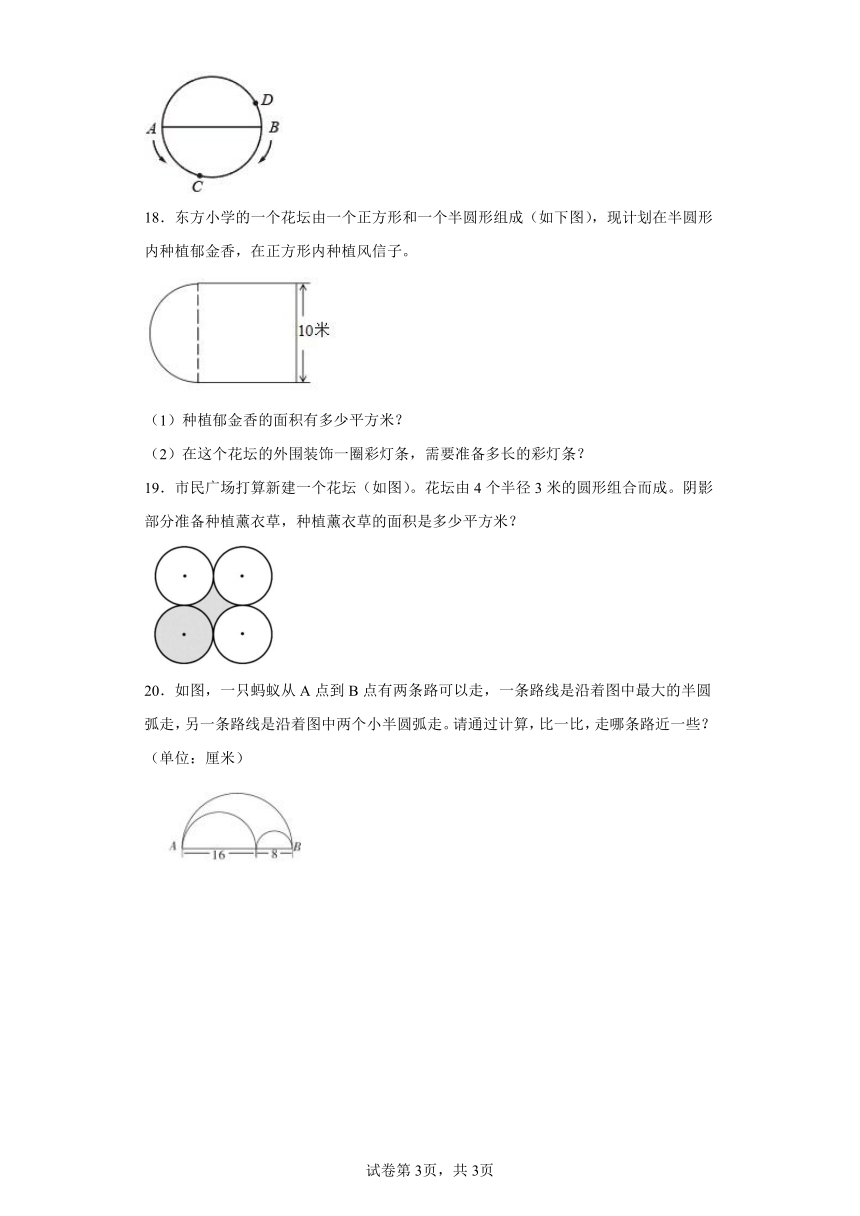
①互质的两个数都是质数。②分子大于分母的分数一定是假分数。③一根绳子分成6段,每段长占全长的。④分数值比较大的分数,分数单位一定大。⑤圆的周长是它直径的倍。
A.1 B.2 C.3 D.4
4.如图,从甲地到乙地有A、B两条路线可以走,这两条路线相比,( )。
A.同样长 B.A路线长 C.B路线长
5.下图中两个正方形的边长相等,下面关于这两个图形阴影部分的说法正确的是( )。
A.面积相等,周长不相等 B.面积相等,周长也相等
C.面积不相等,周长也不相等 D.面积不相等,周长相等
二、图形计算
三、填空题
6.在一个长9cm、宽8cm的长方形中画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2。
7.圆的半径扩大到原来的3倍,周长扩大到原来的( )倍;面积扩大到原来的( )倍。
8.一张长方形纸,长12cm,宽10cm,在这张纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2。
9.图中涂色部分正方形的面积是50平方厘米,圆的面积是( )平方厘米。
10.如图,点O是大圆的圆心,那么小圆的直径是大圆直径的,小圆面积是大圆面积的。
四、判断题
11.半径是2cm的圆,它的周长和面积的大小是相等的。( )
12.半圆的周长等于圆周长的一半。( )
13.圆的周长是这个圆的直径的3.14倍。( )
14.直径4cm的圆比半径2cm的圆大。( )
15.若甲圆的周长是乙圆周长的2倍,则甲圆的面积是乙圆面积的2倍。( )
五、解答题
16.菲菲同学在学完了圆的知识后,想到了苏州的小桥流水,创作了下面一幅图。这幅图由5个完全相同的半圆组合而成,你知道菲菲在画半圆的时候,圆规两脚间的距离是多少吗?(单位:mm)
17.如图,一条圆形跑道,AB是直径。甲乙两人分别从A、B两点出发,按箭头方向前进,他们在离A点75米的C点相遇,接着又在离B点25米的D点相遇。圆形跑道的长是多少米?
18.东方小学的一个花坛由一个正方形和一个半圆形组成(如下图),现计划在半圆形内种植郁金香,在正方形内种植风信子。
(1)种植郁金香的面积有多少平方米?
(2)在这个花坛的外围装饰一圈彩灯条,需要准备多长的彩灯条?
19.市民广场打算新建一个花坛(如图)。花坛由4个半径3米的圆形组合而成。阴影部分准备种植薰衣草,种植薰衣草的面积是多少平方米?
20.如图,一只蚂蚁从A点到B点有两条路可以走,一条路线是沿着图中最大的半圆弧走,另一条路线是沿着图中两个小半圆弧走。请通过计算,比一比,走哪条路近一些?(单位:厘米)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
半圆的周长=整圆周长的一半+一条直径,据此解答即可。
【详解】
2πr÷2+2r
=πr+2r
则它的周长是πr+2r。
故选:B
【点睛】
本题考查圆的周长,明确半圆的周长=整圆周长的一半+一条直径是解题的关键。
2.A
【解析】
【分析】
设乙圆的直径为d,则甲圆的直径就是3d,根据圆的面积公式:S=πr2表示出两圆的面积,求商即可解答。
【详解】
设乙圆的直径为d,则甲圆的直径就是3d。
甲圆的面积:π(3d÷2)2=9π(d÷2)2
乙圆的面积:π(d÷2)2
甲圆的面积是乙圆的:9π(d÷2)2÷π(d÷2)2=9。
故答案为:A
【点睛】
本题主要考查圆的面积公式的灵活应用。
3.B
【解析】
【分析】
逐句分析,找出说法正确的选择即可。
【详解】
①互质的两个数不一定都是质数。例如3和4两个数互质,4是合数。
②分子大于分母的分数一定是大于1的分数,是假分数。原题说法正确。
③一根绳子平均分成6段,每段长占全长的。原题说法错误。
④分数值比较大的分数,分数单位不一定大。比如 < ,> ,原题说法错误。
⑤圆的周长是它直径的倍。说法正确。
所以正确的说法有2个。
故选择:B
【点睛】
此题考查的知识面较为广泛,注意基础知识的积累。
4.A
【解析】
【分析】
由图知道小圆的直径是大圆的半径,利用圆的周长公式C=2πr或πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可。
【详解】
假设小圆的直径为d,则大圆的半径为d,
A路线的长度为:2πd÷2=πd,
B路线的长度为:πd÷2×2=πd;
所以A、B两条路的长度一样长;
故答案为:A。
【点睛】
本题主要是灵活利用圆的周长公式解决问题。
5.A
【解析】
【分析】
根据图可知:第一个图片阴影部分周长:两个半圆弧的周长加上两个正方形的边长,由于两个半圆弧拼起来正好是一个以正方形边长的长度为直径的圆的周长和两个正方形边长和,阴影部分的面积:正方形的面积减去一个以正方形边长的长度为直径的圆的面积;第二个图片的周长是4个圆的周长,相当于一个以正方形边长的长度为直径的圆的周长,由此即可比较;阴影部分的面积:正方形的面积减去一个以正方形边长的长度为直径的圆的面积。由此即可比较。
【详解】
由分析可知,这两个图形阴影部分的周长不相等,面积相等。
故答案为:A。
【点睛】
本题主要考查圆的周长和面积公式,熟练掌握它们的公式并灵活运用。
6. 25.12 50.24
【解析】
【分析】
由题意知:在一个长9cm、宽8cm的长方形中画一个最大的圆,这个圆的直径长度等于长方形的宽,知道圆的直径,利用圆的周长和面积公式即可计算出这个圆的周长和面积。据此解答。
【详解】
圆的周长:8×3.14=25.12(厘米)
圆的面积:3.14×(8÷2)
=3.14×16
=50.24(平方厘米)
【点睛】
理解最大的圆的直径等于长方形的宽,进而利用圆的周长和面积公式求得结果是解答本题的关键。
7. 3 9
【解析】
【分析】
假设圆的半径为1,则扩大后的半径为3,根据“C=2πr”、“S=πr2”计算出变化前的周长和面积,再进行解答即可。
【详解】
假设圆的半径为1,则扩大后的半径为3;
变化前周长:2×π×1=2π;
变化后周长:2×π×4=6π;
6π÷2π=3;
圆的周长扩大到原来的3倍;
变化前面积:π×12=π;
变化后面积:π×32=9π;
9π÷π=9;
面积扩大到原来的9倍
【点睛】
熟练掌握圆的周长和面积公式是解答本题的关键,周长扩大倍数和直径、半径扩大倍数相等,面积扩大倍数是直径、半径扩大倍数的平方。
8. 31.4 78.5
【解析】
【分析】
根据题意可知,圆的直径等于长方形的宽,根据圆的周长C=πd,圆的面积S=πr2,代入数据计算即可。
【详解】
3.14×10=31.4(厘米),圆的周长是31.4厘米;
3.14×(10÷2)2
=3.14×25
=78.5(平方厘米),圆的面积是78.5平方厘米。
【点睛】
此题考查了圆的周长和面积的计算,先确定出圆的直径是解题关键。
9.157
【解析】
【分析】
观察图形可知,正方形的边长等于圆的半径,正方形面积=边长2,圆的面积=π×半径2,圆的面积=π×正方形面积,即:π×50。
【详解】
3.14×50=157(平方厘米)
【点睛】
本题考查正方形面积公式、圆的面积公式的应用,关键是明确正方形边长的平方等于圆的半径的平方。
10.;
【解析】
【分析】
根据图文可知:小圆的直径正好是大圆的半径,那么小圆的直径是大圆直径的,再根据小圆的直径是大圆直径的,可知小圆的半径是大圆半径的,那么小圆的面积是大圆面积的()2=。
【详解】
小圆的直径正好是大圆的半径,
那么小圆的直径是大圆直径的;
则小圆的半径是大圆半径的,
那么小圆的面积是大圆面积的()2=。
【点睛】
解答此题应明确:两个圆的周长的比、半径的比和直径的比都相等;面积的比即半径的平方比。
11.×
【解析】
【分析】
周长是长度,面积是图形所占平面的大小,不能比较。
【详解】
半径是2cm的圆,它的周长和面积的大小是相等的,说法错误。
故答案为:×。
【点睛】
本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积概念。
12.×
【解析】
【分析】
半圆和圆周长的一半不一样,半圆的周长=圆周长的一半+一条直径的长度,据此解答。
【详解】
如图所示,半圆的周长大于圆周长的一半。
故答案为:×
【点睛】
掌握半圆和圆周长的一半的区别是解答题目的关键。
13.×
【解析】
【分析】
根据圆周率的含义:圆周率等于圆的周长和它直径的比值,用字母“π”表示,由此解答即可
【详解】
由分析可知:
圆的周长是这个圆的直径的π倍。故本题说法错误。
【点睛】
此题考查了圆的基础知识,应注意基础知识的积累和理解。
14.×
【解析】
【分析】
圆的大小是由半径决定的,求出直径是4厘米圆的半径,再比较半径的长度,即可解答。
【详解】
4÷2=2(cm)
2cm=2cm
直径是4cm的圆等于半径2cm的圆
原题说法是错误的
故答案为:×
【点睛】
本题考查圆的大小,圆的大小是由圆的半径决定的,半径相等,圆也相等。
15.×
【解析】
【分析】
甲圆的周长是乙圆周长的2倍,也就是说甲圆的半径是乙圆半径的2倍,设乙圆的半径为r,则甲圆半径为2r,根据圆的面积公式πr2,求出甲圆的面积和乙圆的面积,在进行判断,即可解答。
【详解】
甲圆的周长是乙圆周长的2倍,则甲圆的半径是乙圆半径的2倍,设乙圆半径为r,则甲圆半径为2r
甲圆面积:π(2r)2=4πr2
乙圆面积:πr2
甲圆面积÷乙圆面积=4πr2÷πr2=4倍
若甲圆的的周长是乙圆周长的2倍,则甲圆的面积是乙圆面积的4倍
原题若甲圆的周长是乙圆周长的2倍,则甲圆的面积是乙圆面积的2倍是错误的
故答案为:×
【点睛】
本题考查圆的周长公式、面积公式的应用,熟记公式,灵活应用。
16.18毫米
【解析】
【分析】
观察图形可知,上半部分是三个直径与两个12毫米的和,下半部分是两个直径与两个22毫米一个16毫米的和,设:圆的直径为x毫米。列方程:3x+12×2=2x+22×2+16,解方程,求出直径,再除以2,就是这个圆规两脚之间的距离。
【详解】
解:设圆的直径为x毫米
3x+12×2=2x+22×2+16
3x+24=2x+44+16
3x-2x=60-24
x=36
36÷2=18(毫米)
答:圆规两脚的距离是18毫米。
【点睛】
本题考查方程的实际应用,根据题意找出相关的量,列方程,解方程。
17.400米
【解析】
【分析】
由于甲、乙两人分别从圆形跑道直径AB两端同时出发相向而行,则第一次相遇时二人共行了半个圆周,甲行了AC=75米,即每行半个圆周,甲就行75米,第二次相遇,二人共行了1.5个圆周,则甲应该行:75×3=225米,即:AD=225米,又:BD=25米,所以所以半个圆周:AB=AD-BD=225-25=200(米),由此即能求出圆的周长。
【详解】
(75×3-25)×2
=(225-25)×2
=200×2
=400(米)
答:圆形跑道的长是400米。
【点睛】
明确所给条件求出圆的周长是完成本题的关键.本题通过画图分析更直观一些。
18.(1)39.25平方米
(2)45.7米
【解析】
【分析】
(1)圆的面积=πr2,据此求出整圆的面积,再除以2即可求出半圆的面积。
(2)彩灯条的长度就是花坛的周长。观察图形可知,花坛的周长包括圆周长的一半和正方形的3条边。圆的周长=πd,据此求出圆周长的一半,再加上正方形的3条边即可。
【详解】
(1)3.14×(10÷2)2÷2
=3.14×25÷2
=39.25(平方米)
答:种植郁金香的面积有39.25平方米。
(2)3.14×10÷2+10×3
=15.7+30
=45.7(米)
答:需要准备45.7米的彩灯条。
【点睛】
本题主要考查圆的面积和含圆的图形的周长。理解图形周长的意义是解题的关键。
19.36平方米
【解析】
【分析】
观察图形可知,阴影部分面积是一个半径为3米圆的面积,与边长为6米的正方形减去一个半径为3米圆的面积的差的和,根据圆的面积公式:π×半径2;正方形面积公式:边长×边长,代入数据,即可解答。
【详解】
3.14×32+[(3+3)×(3+3)-3.14×32]
=3.14×9+[6×6-3.14×9]
=3.14×9+36-3.14×9
=36(平方米)
答:种植薰衣草的面积是36平方米。
【点睛】
本题考查圆的面积与正方形面积公式的运用,关键是4个圆中心部分的面积是边长等于圆直径的正方形面积减去半径为3米圆面积。
20.一样近
【解析】
【分析】
根据圆的周长公式,求出最大半圆的半弧长,再求出两个小半圆弧长的和,进行比较,即可解答。
【详解】
最大半圆弧长:
3.14×(16+8)÷2
=3.14×24÷2
=75.36÷2
=37.68(厘米)
两个小半圆弧长:
3.14×16÷2+3.14×8÷2
=50.24÷2+25.12÷2
=25.12+12.56
=37.68(厘米)
37.68=37.68
这两条路一样近
答:这两条路一样近。
【点睛】
本题考查圆的周长公式的运用,熟记公式,灵活运用。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.一个半圆,半径是r,它的周长是( )。
A. B. C.
2.甲圆的直径是乙圆的3倍,甲圆的面积是乙圆的( )倍。
A.9 B.6 C. D.3
3.下列说法,正确的有( )个。
①互质的两个数都是质数。②分子大于分母的分数一定是假分数。③一根绳子分成6段,每段长占全长的。④分数值比较大的分数,分数单位一定大。⑤圆的周长是它直径的倍。
A.1 B.2 C.3 D.4
4.如图,从甲地到乙地有A、B两条路线可以走,这两条路线相比,( )。
A.同样长 B.A路线长 C.B路线长
5.下图中两个正方形的边长相等,下面关于这两个图形阴影部分的说法正确的是( )。
A.面积相等,周长不相等 B.面积相等,周长也相等
C.面积不相等,周长也不相等 D.面积不相等,周长相等
二、图形计算
三、填空题
6.在一个长9cm、宽8cm的长方形中画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2。
7.圆的半径扩大到原来的3倍,周长扩大到原来的( )倍;面积扩大到原来的( )倍。
8.一张长方形纸,长12cm,宽10cm,在这张纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2。
9.图中涂色部分正方形的面积是50平方厘米,圆的面积是( )平方厘米。
10.如图,点O是大圆的圆心,那么小圆的直径是大圆直径的,小圆面积是大圆面积的。
四、判断题
11.半径是2cm的圆,它的周长和面积的大小是相等的。( )
12.半圆的周长等于圆周长的一半。( )
13.圆的周长是这个圆的直径的3.14倍。( )
14.直径4cm的圆比半径2cm的圆大。( )
15.若甲圆的周长是乙圆周长的2倍,则甲圆的面积是乙圆面积的2倍。( )
五、解答题
16.菲菲同学在学完了圆的知识后,想到了苏州的小桥流水,创作了下面一幅图。这幅图由5个完全相同的半圆组合而成,你知道菲菲在画半圆的时候,圆规两脚间的距离是多少吗?(单位:mm)
17.如图,一条圆形跑道,AB是直径。甲乙两人分别从A、B两点出发,按箭头方向前进,他们在离A点75米的C点相遇,接着又在离B点25米的D点相遇。圆形跑道的长是多少米?
18.东方小学的一个花坛由一个正方形和一个半圆形组成(如下图),现计划在半圆形内种植郁金香,在正方形内种植风信子。
(1)种植郁金香的面积有多少平方米?
(2)在这个花坛的外围装饰一圈彩灯条,需要准备多长的彩灯条?
19.市民广场打算新建一个花坛(如图)。花坛由4个半径3米的圆形组合而成。阴影部分准备种植薰衣草,种植薰衣草的面积是多少平方米?
20.如图,一只蚂蚁从A点到B点有两条路可以走,一条路线是沿着图中最大的半圆弧走,另一条路线是沿着图中两个小半圆弧走。请通过计算,比一比,走哪条路近一些?(单位:厘米)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
半圆的周长=整圆周长的一半+一条直径,据此解答即可。
【详解】
2πr÷2+2r
=πr+2r
则它的周长是πr+2r。
故选:B
【点睛】
本题考查圆的周长,明确半圆的周长=整圆周长的一半+一条直径是解题的关键。
2.A
【解析】
【分析】
设乙圆的直径为d,则甲圆的直径就是3d,根据圆的面积公式:S=πr2表示出两圆的面积,求商即可解答。
【详解】
设乙圆的直径为d,则甲圆的直径就是3d。
甲圆的面积:π(3d÷2)2=9π(d÷2)2
乙圆的面积:π(d÷2)2
甲圆的面积是乙圆的:9π(d÷2)2÷π(d÷2)2=9。
故答案为:A
【点睛】
本题主要考查圆的面积公式的灵活应用。
3.B
【解析】
【分析】
逐句分析,找出说法正确的选择即可。
【详解】
①互质的两个数不一定都是质数。例如3和4两个数互质,4是合数。
②分子大于分母的分数一定是大于1的分数,是假分数。原题说法正确。
③一根绳子平均分成6段,每段长占全长的。原题说法错误。
④分数值比较大的分数,分数单位不一定大。比如 < ,> ,原题说法错误。
⑤圆的周长是它直径的倍。说法正确。
所以正确的说法有2个。
故选择:B
【点睛】
此题考查的知识面较为广泛,注意基础知识的积累。
4.A
【解析】
【分析】
由图知道小圆的直径是大圆的半径,利用圆的周长公式C=2πr或πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可。
【详解】
假设小圆的直径为d,则大圆的半径为d,
A路线的长度为:2πd÷2=πd,
B路线的长度为:πd÷2×2=πd;
所以A、B两条路的长度一样长;
故答案为:A。
【点睛】
本题主要是灵活利用圆的周长公式解决问题。
5.A
【解析】
【分析】
根据图可知:第一个图片阴影部分周长:两个半圆弧的周长加上两个正方形的边长,由于两个半圆弧拼起来正好是一个以正方形边长的长度为直径的圆的周长和两个正方形边长和,阴影部分的面积:正方形的面积减去一个以正方形边长的长度为直径的圆的面积;第二个图片的周长是4个圆的周长,相当于一个以正方形边长的长度为直径的圆的周长,由此即可比较;阴影部分的面积:正方形的面积减去一个以正方形边长的长度为直径的圆的面积。由此即可比较。
【详解】
由分析可知,这两个图形阴影部分的周长不相等,面积相等。
故答案为:A。
【点睛】
本题主要考查圆的周长和面积公式,熟练掌握它们的公式并灵活运用。
6. 25.12 50.24
【解析】
【分析】
由题意知:在一个长9cm、宽8cm的长方形中画一个最大的圆,这个圆的直径长度等于长方形的宽,知道圆的直径,利用圆的周长和面积公式即可计算出这个圆的周长和面积。据此解答。
【详解】
圆的周长:8×3.14=25.12(厘米)
圆的面积:3.14×(8÷2)
=3.14×16
=50.24(平方厘米)
【点睛】
理解最大的圆的直径等于长方形的宽,进而利用圆的周长和面积公式求得结果是解答本题的关键。
7. 3 9
【解析】
【分析】
假设圆的半径为1,则扩大后的半径为3,根据“C=2πr”、“S=πr2”计算出变化前的周长和面积,再进行解答即可。
【详解】
假设圆的半径为1,则扩大后的半径为3;
变化前周长:2×π×1=2π;
变化后周长:2×π×4=6π;
6π÷2π=3;
圆的周长扩大到原来的3倍;
变化前面积:π×12=π;
变化后面积:π×32=9π;
9π÷π=9;
面积扩大到原来的9倍
【点睛】
熟练掌握圆的周长和面积公式是解答本题的关键,周长扩大倍数和直径、半径扩大倍数相等,面积扩大倍数是直径、半径扩大倍数的平方。
8. 31.4 78.5
【解析】
【分析】
根据题意可知,圆的直径等于长方形的宽,根据圆的周长C=πd,圆的面积S=πr2,代入数据计算即可。
【详解】
3.14×10=31.4(厘米),圆的周长是31.4厘米;
3.14×(10÷2)2
=3.14×25
=78.5(平方厘米),圆的面积是78.5平方厘米。
【点睛】
此题考查了圆的周长和面积的计算,先确定出圆的直径是解题关键。
9.157
【解析】
【分析】
观察图形可知,正方形的边长等于圆的半径,正方形面积=边长2,圆的面积=π×半径2,圆的面积=π×正方形面积,即:π×50。
【详解】
3.14×50=157(平方厘米)
【点睛】
本题考查正方形面积公式、圆的面积公式的应用,关键是明确正方形边长的平方等于圆的半径的平方。
10.;
【解析】
【分析】
根据图文可知:小圆的直径正好是大圆的半径,那么小圆的直径是大圆直径的,再根据小圆的直径是大圆直径的,可知小圆的半径是大圆半径的,那么小圆的面积是大圆面积的()2=。
【详解】
小圆的直径正好是大圆的半径,
那么小圆的直径是大圆直径的;
则小圆的半径是大圆半径的,
那么小圆的面积是大圆面积的()2=。
【点睛】
解答此题应明确:两个圆的周长的比、半径的比和直径的比都相等;面积的比即半径的平方比。
11.×
【解析】
【分析】
周长是长度,面积是图形所占平面的大小,不能比较。
【详解】
半径是2cm的圆,它的周长和面积的大小是相等的,说法错误。
故答案为:×。
【点睛】
本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积概念。
12.×
【解析】
【分析】
半圆和圆周长的一半不一样,半圆的周长=圆周长的一半+一条直径的长度,据此解答。
【详解】
如图所示,半圆的周长大于圆周长的一半。
故答案为:×
【点睛】
掌握半圆和圆周长的一半的区别是解答题目的关键。
13.×
【解析】
【分析】
根据圆周率的含义:圆周率等于圆的周长和它直径的比值,用字母“π”表示,由此解答即可
【详解】
由分析可知:
圆的周长是这个圆的直径的π倍。故本题说法错误。
【点睛】
此题考查了圆的基础知识,应注意基础知识的积累和理解。
14.×
【解析】
【分析】
圆的大小是由半径决定的,求出直径是4厘米圆的半径,再比较半径的长度,即可解答。
【详解】
4÷2=2(cm)
2cm=2cm
直径是4cm的圆等于半径2cm的圆
原题说法是错误的
故答案为:×
【点睛】
本题考查圆的大小,圆的大小是由圆的半径决定的,半径相等,圆也相等。
15.×
【解析】
【分析】
甲圆的周长是乙圆周长的2倍,也就是说甲圆的半径是乙圆半径的2倍,设乙圆的半径为r,则甲圆半径为2r,根据圆的面积公式πr2,求出甲圆的面积和乙圆的面积,在进行判断,即可解答。
【详解】
甲圆的周长是乙圆周长的2倍,则甲圆的半径是乙圆半径的2倍,设乙圆半径为r,则甲圆半径为2r
甲圆面积:π(2r)2=4πr2
乙圆面积:πr2
甲圆面积÷乙圆面积=4πr2÷πr2=4倍
若甲圆的的周长是乙圆周长的2倍,则甲圆的面积是乙圆面积的4倍
原题若甲圆的周长是乙圆周长的2倍,则甲圆的面积是乙圆面积的2倍是错误的
故答案为:×
【点睛】
本题考查圆的周长公式、面积公式的应用,熟记公式,灵活应用。
16.18毫米
【解析】
【分析】
观察图形可知,上半部分是三个直径与两个12毫米的和,下半部分是两个直径与两个22毫米一个16毫米的和,设:圆的直径为x毫米。列方程:3x+12×2=2x+22×2+16,解方程,求出直径,再除以2,就是这个圆规两脚之间的距离。
【详解】
解:设圆的直径为x毫米
3x+12×2=2x+22×2+16
3x+24=2x+44+16
3x-2x=60-24
x=36
36÷2=18(毫米)
答:圆规两脚的距离是18毫米。
【点睛】
本题考查方程的实际应用,根据题意找出相关的量,列方程,解方程。
17.400米
【解析】
【分析】
由于甲、乙两人分别从圆形跑道直径AB两端同时出发相向而行,则第一次相遇时二人共行了半个圆周,甲行了AC=75米,即每行半个圆周,甲就行75米,第二次相遇,二人共行了1.5个圆周,则甲应该行:75×3=225米,即:AD=225米,又:BD=25米,所以所以半个圆周:AB=AD-BD=225-25=200(米),由此即能求出圆的周长。
【详解】
(75×3-25)×2
=(225-25)×2
=200×2
=400(米)
答:圆形跑道的长是400米。
【点睛】
明确所给条件求出圆的周长是完成本题的关键.本题通过画图分析更直观一些。
18.(1)39.25平方米
(2)45.7米
【解析】
【分析】
(1)圆的面积=πr2,据此求出整圆的面积,再除以2即可求出半圆的面积。
(2)彩灯条的长度就是花坛的周长。观察图形可知,花坛的周长包括圆周长的一半和正方形的3条边。圆的周长=πd,据此求出圆周长的一半,再加上正方形的3条边即可。
【详解】
(1)3.14×(10÷2)2÷2
=3.14×25÷2
=39.25(平方米)
答:种植郁金香的面积有39.25平方米。
(2)3.14×10÷2+10×3
=15.7+30
=45.7(米)
答:需要准备45.7米的彩灯条。
【点睛】
本题主要考查圆的面积和含圆的图形的周长。理解图形周长的意义是解题的关键。
19.36平方米
【解析】
【分析】
观察图形可知,阴影部分面积是一个半径为3米圆的面积,与边长为6米的正方形减去一个半径为3米圆的面积的差的和,根据圆的面积公式:π×半径2;正方形面积公式:边长×边长,代入数据,即可解答。
【详解】
3.14×32+[(3+3)×(3+3)-3.14×32]
=3.14×9+[6×6-3.14×9]
=3.14×9+36-3.14×9
=36(平方米)
答:种植薰衣草的面积是36平方米。
【点睛】
本题考查圆的面积与正方形面积公式的运用,关键是4个圆中心部分的面积是边长等于圆直径的正方形面积减去半径为3米圆面积。
20.一样近
【解析】
【分析】
根据圆的周长公式,求出最大半圆的半弧长,再求出两个小半圆弧长的和,进行比较,即可解答。
【详解】
最大半圆弧长:
3.14×(16+8)÷2
=3.14×24÷2
=75.36÷2
=37.68(厘米)
两个小半圆弧长:
3.14×16÷2+3.14×8÷2
=50.24÷2+25.12÷2
=25.12+12.56
=37.68(厘米)
37.68=37.68
这两条路一样近
答:这两条路一样近。
【点睛】
本题考查圆的周长公式的运用,熟记公式,灵活运用。
答案第1页,共2页
答案第1页,共2页
