苏教版数学五年级下册 七解决问题的策略 单元综合练(word版 含解析)
文档属性
| 名称 | 苏教版数学五年级下册 七解决问题的策略 单元综合练(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 14:31:55 | ||
图片预览




文档简介
苏教版五年级下册 七 解决问题的策略 单元综合练
一、选择题
1.下面运用了“转化”思想方法的是( )
A.① B.②③ C.②③④ D.①②③④
2.比较下面三个三角形中的涂色部分面积大小(每个扇形的半径为1cm)结果是( )。
A.第一个最大 B.第三个最大 C.一样大
3.10+11+12+13+14+15=( )。
A.76 B.75 C.65
4.按规律: 上要画的图是( )。
A. B. C. D.
5.在甲组图形的四个图中,每个图是由四中简单图A、B、C、D(不同的线段或圆)中的某两个图形构成的,例如由A、B组成的图形记为A*B,在乙组图形的(a)(b)(c)(d)四个图中,表示“A*D”和“A*C"的是( )。
A.(a)和(b) B.(b)和(c) C.(c)和(d) D.(b)和(d)
二、填空题
6.将一些▲按一定的规律摆放(如图所示),图形中▲的个数依次是6、10、16、24……
第7个图形中有( )个▲,第10个图形中有( )个▲。
7.将小正方体按下图的方式摆放:摆1个小正方体有5个面露在外面,摆2个小正方体有8个面露在外面,摆3个小正方体有( )个面露在外面,摆n个小正方体有( )个面露在外面。
8.观察下列式子:,,,……
请计算( )。
三、解答题
9.修一条路,第一天修了全长的一半多6米,第二天修了余下的一半少20米,第三天修了30米,最后还剩14米没修.这条路长多少米?
10.一张桌子可以坐6人,两张桌子拼起来可以坐10人,三张桌子拼起来可以坐14人.像这样共几张桌子拼起来可以坐50人?
11.先计算下面各题,然后找出规律。
(1)=
(2)=
(3)=
12.计算,把正方形看作单位“1”,把算式的加数填入下图,再计算。
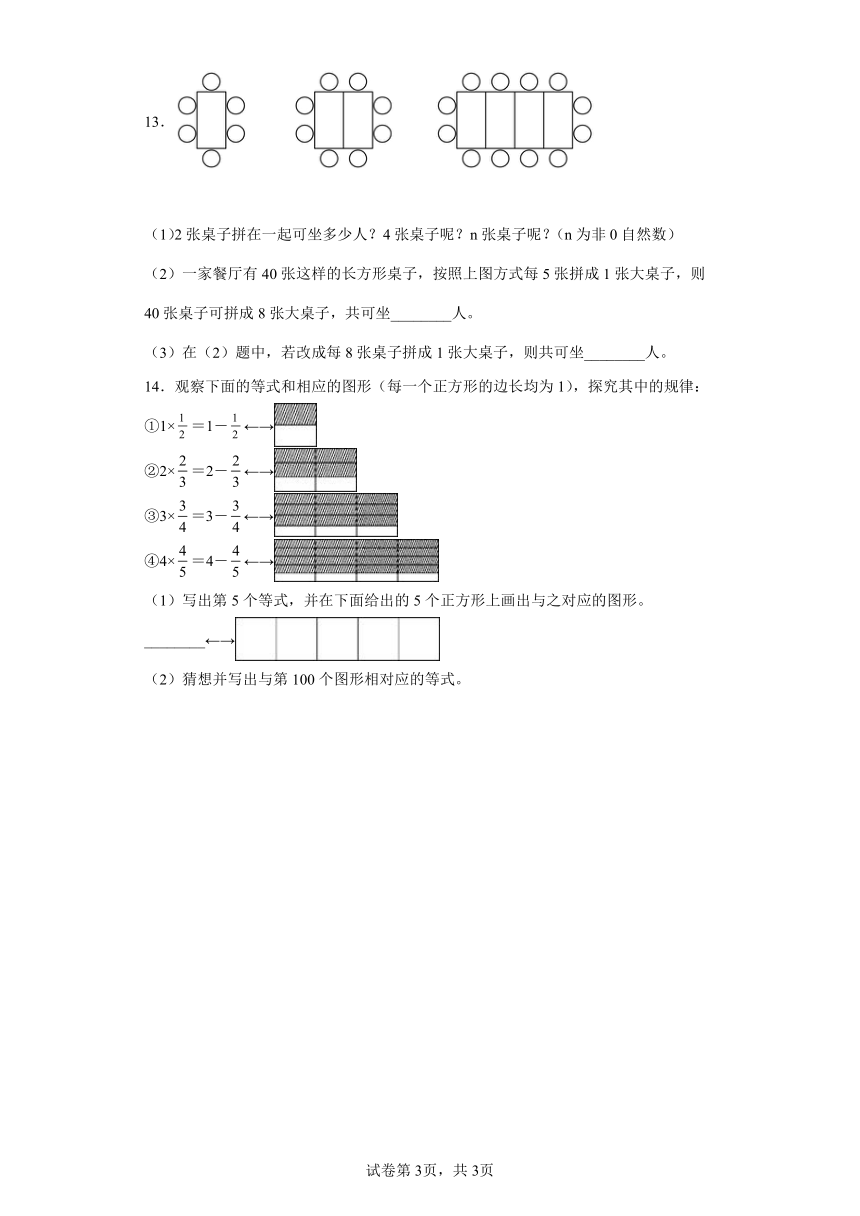
13.
(1)2张桌子拼在一起可坐多少人?4张桌子呢?n张桌子呢?(n为非0自然数)
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐________人。
(3)在(2)题中,若改成每8张桌子拼成1张大桌子,则共可坐________人。
14.观察下面的等式和相应的图形(每一个正方形的边长均为1),探究其中的规律:
①1×=1-←→
②2×=2-←→
③3×=3-←→
④4×=4-←→
(1)写出第5个等式,并在下面给出的5个正方形上画出与之对应的图形。
________←→
(2)猜想并写出与第100个图形相对应的等式。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
转化思想是数学学习中常用的数学思想,逐项分析,新内容是转化成了哪个已学内容即可。
【详解】
①是将小数乘法转化为整数乘法;是将圆柱体积转化成了长方体体积;
②是将平行四边形面积转化为长方形面积;
③把异分母分数相加减转化为同分母分数进行计算;
④是将五边形内角和转化为三角形内角和。
故答案为:D。
【点睛】
转化的目的是不断发现问题,分析问题,最终解决问题。
2.C
【解析】
【分析】
因为每个扇形的半径为1cm,三角形内角和等于180°,所以可以将①②③三幅图中阴影部分面积转化为半径是1cm的半圆面积,据此解答即可。
【详解】
由分析可得,三幅图中阴影部分面积都是半径为1厘米的半圆面积;
3.14×12÷2=1.57(平方厘米)
故答案为:C
【点睛】
巧妙利用转化思想是解题关键。
3.B
【解析】
【分析】
根据数据特点,10+15=11+14=12+13,据此计算即可。
【详解】
10+11+12+13+14+15
=(10+15)+(11+14)+(12+13)
=25×3
=75
故答案为:B
【点睛】
本题也可以直接计算得出答案。
4.D
【解析】
【分析】
观察可知,图形每次顺时针旋转90°,据此分析。
【详解】
如图 。
故答案为:D
【点睛】
关键是观察前后图形之间的变化规律,注意旋转方向和角度。
5.D
【解析】
【分析】
根据图形发现规律:由甲组的A*B,B*C,B*D可知,B为较大的圆,A为竖线,C为横线,D为较小的圆,据此解答。
【详解】
根据图意,由甲组的A* B, B*C, B* D可知,B为较大的圆,A为竖线,C为横线,D为较小的圆,所以: A* D为b, A* C为d,所以答案为: D。
【点睛】
本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
6. 60 114
【解析】
【分析】
先观察每个图形的最外侧都有4个▲,再观察每个图形内部▲的行数和列数,则有第1个图形中有4+1×2=6个▲,第2个图形中有4+2×3=10个▲,第3个图形中有4+3×4=16个▲,则第7个图形中有4+7×(7+1)个▲,则第10个图形中有4+10×(10+1)个▲,据此规律解答。
【详解】
根据分析可知,第7个图形共有:
4+7×(7+1)
=4+56
=60(个)
第10个图形中共有:
4+10×(10+1)
=4+110
=114(个)
第7个图形共有60个▲,第10个图形中共有114个▲。
【点睛】
本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
7. 11 3n+2
【解析】
【分析】
观察小正方体的摆放可以发现,摆放图形的左右2个侧面总是露在外面,而前面、后面和上面3个面中露在外面的面的个数都等于小正方体的个数,则整个图形露在外面的面的个数=小正方体的个数×3+2,据此解答。
【详解】
3×3+2=11(个),则摆3个小正方体有11个面露在外面;摆n个小正方体有 3n+2(或2+3n)个面露在外面。
【点睛】
本题考查数形结合问题。数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
8.
【解析】
【分析】
将原式化为:()+()+()+……(-),再去括号简算即可。
【详解】
=()+()+()+(-)+(-)+(-)+(-)+(-)+(-)
=+++-+-+-+-+-+-
=1-
=
【点睛】
本题主要考查的灵活应用。
9.108米
【解析】
【分析】
要求这条路长多少米,通过题意可知,如果第二天正好修了余下的一半,则剩下30+14﹣20=24米,用24×2则算出余下的长度;又因为第一天修了全长的一半多6米,如果第一天正好修了全长的一半时,则剩下(24×2+6)米;这样得出剩下的长度的2倍即全长;由此进行解答即可.
【详解】
(30+14﹣20)×2
=24×2
=48(米)
(48+6)×2=108(米)
答:这条路长108米.
【点睛】
解决此类问题的关键是抓住最后得到的数量,从后向前进行推理,根据加减乘除的逆运算思维进行解答.
10.12张
【解析】
【分析】
第一张桌子可以坐6人;
拼2张桌子可以坐6+4×1=10人;
拼3张桌子可以坐6+4×2=14人;
故n张桌子拼在一起可以坐6+4(n-1)=4n+2.
【详解】
解:设第n张桌子可以坐50人.
4n+2=50
n=12
答:像这样12张桌子拼起来可以坐50人.
11.(1);(2);(3)
规律:后一种加数是前一个加数的一半的连加算式的和是:1减最后一个加数的差,即分母是最后一个加数的分母,分子比分母少1。
【解析】
【分析】
这三个算式中每一个相加的加数中后一个加数的分母是前一个加数分母的2倍,可以利用拆项法分别算出算式(1)和是、算式(2)和是、算式(3)和是,通过比较可知,这三个算式的和正好分别是1减最后一个加数的差,由此解答。
【详解】
(1),
=
=1-+-+-
=1-
=
(2)+++
=(1-)+(-)+(-)+(-)
=1+-+-+-
=1-
=
(3)++++
=(1-)+(-)+(-)+(-)+(-)
=1-+-+-+-+-
=1-
=
规律是:后一种加数是前一个加数的一半的连加算式的和是:1减最后一个加数的差,即分母是最后一个加数的分母,分子比分母少1。
【点评】
此题主要考查利用拆项法求和的方法。
12.图见解析;
【解析】
【分析】
根据分数的意义,把单位“1”平均分成若干份,表示这样的一份或几份的数叫分数,填空解答即可。
【详解】
如图:;
==
【点睛】
理解并能运用数形结合的思想解题是关键。
13.(1)8人;12人;(2n+4)人
(2)112
(3)100
【解析】
【分析】
(1)根据图示,发现这组图形的规律:1张桌子可坐人数:6人;2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)根据(1)的规律可知:5张桌子拼一块,可坐人数:2×5+4=14(人).40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)由(1)知,每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
据此解答.
【详解】
(1)2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)5张桌子拼一块,可坐人数:2×5+4=14(人),40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
【点睛】
本题主要考查数与形结合的规律,关键根据所给图形发现这组图形的规律,并运用规律解决问题。
14.(1)5×=5-;作图见详解
(2)100×=100-
【解析】
【分析】
观察可知,第几个等式对应第一个乘数和第二个乘数的分子就是几,分母是分子+1;图形对应规律是第几个等式就将图形平均分成几份,分子是几涂几份。
【详解】
(1)5×=5-;
(2)100×=100-
【点睛】
在探索数与形结合的规律时,要考虑数的排列规律,通过数形结合、对应等方法来解决问题。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.下面运用了“转化”思想方法的是( )
A.① B.②③ C.②③④ D.①②③④
2.比较下面三个三角形中的涂色部分面积大小(每个扇形的半径为1cm)结果是( )。
A.第一个最大 B.第三个最大 C.一样大
3.10+11+12+13+14+15=( )。
A.76 B.75 C.65
4.按规律: 上要画的图是( )。
A. B. C. D.
5.在甲组图形的四个图中,每个图是由四中简单图A、B、C、D(不同的线段或圆)中的某两个图形构成的,例如由A、B组成的图形记为A*B,在乙组图形的(a)(b)(c)(d)四个图中,表示“A*D”和“A*C"的是( )。
A.(a)和(b) B.(b)和(c) C.(c)和(d) D.(b)和(d)
二、填空题
6.将一些▲按一定的规律摆放(如图所示),图形中▲的个数依次是6、10、16、24……
第7个图形中有( )个▲,第10个图形中有( )个▲。
7.将小正方体按下图的方式摆放:摆1个小正方体有5个面露在外面,摆2个小正方体有8个面露在外面,摆3个小正方体有( )个面露在外面,摆n个小正方体有( )个面露在外面。
8.观察下列式子:,,,……
请计算( )。
三、解答题
9.修一条路,第一天修了全长的一半多6米,第二天修了余下的一半少20米,第三天修了30米,最后还剩14米没修.这条路长多少米?
10.一张桌子可以坐6人,两张桌子拼起来可以坐10人,三张桌子拼起来可以坐14人.像这样共几张桌子拼起来可以坐50人?
11.先计算下面各题,然后找出规律。
(1)=
(2)=
(3)=
12.计算,把正方形看作单位“1”,把算式的加数填入下图,再计算。
13.
(1)2张桌子拼在一起可坐多少人?4张桌子呢?n张桌子呢?(n为非0自然数)
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐________人。
(3)在(2)题中,若改成每8张桌子拼成1张大桌子,则共可坐________人。
14.观察下面的等式和相应的图形(每一个正方形的边长均为1),探究其中的规律:
①1×=1-←→
②2×=2-←→
③3×=3-←→
④4×=4-←→
(1)写出第5个等式,并在下面给出的5个正方形上画出与之对应的图形。
________←→
(2)猜想并写出与第100个图形相对应的等式。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
转化思想是数学学习中常用的数学思想,逐项分析,新内容是转化成了哪个已学内容即可。
【详解】
①是将小数乘法转化为整数乘法;是将圆柱体积转化成了长方体体积;
②是将平行四边形面积转化为长方形面积;
③把异分母分数相加减转化为同分母分数进行计算;
④是将五边形内角和转化为三角形内角和。
故答案为:D。
【点睛】
转化的目的是不断发现问题,分析问题,最终解决问题。
2.C
【解析】
【分析】
因为每个扇形的半径为1cm,三角形内角和等于180°,所以可以将①②③三幅图中阴影部分面积转化为半径是1cm的半圆面积,据此解答即可。
【详解】
由分析可得,三幅图中阴影部分面积都是半径为1厘米的半圆面积;
3.14×12÷2=1.57(平方厘米)
故答案为:C
【点睛】
巧妙利用转化思想是解题关键。
3.B
【解析】
【分析】
根据数据特点,10+15=11+14=12+13,据此计算即可。
【详解】
10+11+12+13+14+15
=(10+15)+(11+14)+(12+13)
=25×3
=75
故答案为:B
【点睛】
本题也可以直接计算得出答案。
4.D
【解析】
【分析】
观察可知,图形每次顺时针旋转90°,据此分析。
【详解】
如图 。
故答案为:D
【点睛】
关键是观察前后图形之间的变化规律,注意旋转方向和角度。
5.D
【解析】
【分析】
根据图形发现规律:由甲组的A*B,B*C,B*D可知,B为较大的圆,A为竖线,C为横线,D为较小的圆,据此解答。
【详解】
根据图意,由甲组的A* B, B*C, B* D可知,B为较大的圆,A为竖线,C为横线,D为较小的圆,所以: A* D为b, A* C为d,所以答案为: D。
【点睛】
本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
6. 60 114
【解析】
【分析】
先观察每个图形的最外侧都有4个▲,再观察每个图形内部▲的行数和列数,则有第1个图形中有4+1×2=6个▲,第2个图形中有4+2×3=10个▲,第3个图形中有4+3×4=16个▲,则第7个图形中有4+7×(7+1)个▲,则第10个图形中有4+10×(10+1)个▲,据此规律解答。
【详解】
根据分析可知,第7个图形共有:
4+7×(7+1)
=4+56
=60(个)
第10个图形中共有:
4+10×(10+1)
=4+110
=114(个)
第7个图形共有60个▲,第10个图形中共有114个▲。
【点睛】
本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
7. 11 3n+2
【解析】
【分析】
观察小正方体的摆放可以发现,摆放图形的左右2个侧面总是露在外面,而前面、后面和上面3个面中露在外面的面的个数都等于小正方体的个数,则整个图形露在外面的面的个数=小正方体的个数×3+2,据此解答。
【详解】
3×3+2=11(个),则摆3个小正方体有11个面露在外面;摆n个小正方体有 3n+2(或2+3n)个面露在外面。
【点睛】
本题考查数形结合问题。数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
8.
【解析】
【分析】
将原式化为:()+()+()+……(-),再去括号简算即可。
【详解】
=()+()+()+(-)+(-)+(-)+(-)+(-)+(-)
=+++-+-+-+-+-+-
=1-
=
【点睛】
本题主要考查的灵活应用。
9.108米
【解析】
【分析】
要求这条路长多少米,通过题意可知,如果第二天正好修了余下的一半,则剩下30+14﹣20=24米,用24×2则算出余下的长度;又因为第一天修了全长的一半多6米,如果第一天正好修了全长的一半时,则剩下(24×2+6)米;这样得出剩下的长度的2倍即全长;由此进行解答即可.
【详解】
(30+14﹣20)×2
=24×2
=48(米)
(48+6)×2=108(米)
答:这条路长108米.
【点睛】
解决此类问题的关键是抓住最后得到的数量,从后向前进行推理,根据加减乘除的逆运算思维进行解答.
10.12张
【解析】
【分析】
第一张桌子可以坐6人;
拼2张桌子可以坐6+4×1=10人;
拼3张桌子可以坐6+4×2=14人;
故n张桌子拼在一起可以坐6+4(n-1)=4n+2.
【详解】
解:设第n张桌子可以坐50人.
4n+2=50
n=12
答:像这样12张桌子拼起来可以坐50人.
11.(1);(2);(3)
规律:后一种加数是前一个加数的一半的连加算式的和是:1减最后一个加数的差,即分母是最后一个加数的分母,分子比分母少1。
【解析】
【分析】
这三个算式中每一个相加的加数中后一个加数的分母是前一个加数分母的2倍,可以利用拆项法分别算出算式(1)和是、算式(2)和是、算式(3)和是,通过比较可知,这三个算式的和正好分别是1减最后一个加数的差,由此解答。
【详解】
(1),
=
=1-+-+-
=1-
=
(2)+++
=(1-)+(-)+(-)+(-)
=1+-+-+-
=1-
=
(3)++++
=(1-)+(-)+(-)+(-)+(-)
=1-+-+-+-+-
=1-
=
规律是:后一种加数是前一个加数的一半的连加算式的和是:1减最后一个加数的差,即分母是最后一个加数的分母,分子比分母少1。
【点评】
此题主要考查利用拆项法求和的方法。
12.图见解析;
【解析】
【分析】
根据分数的意义,把单位“1”平均分成若干份,表示这样的一份或几份的数叫分数,填空解答即可。
【详解】
如图:;
==
【点睛】
理解并能运用数形结合的思想解题是关键。
13.(1)8人;12人;(2n+4)人
(2)112
(3)100
【解析】
【分析】
(1)根据图示,发现这组图形的规律:1张桌子可坐人数:6人;2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)根据(1)的规律可知:5张桌子拼一块,可坐人数:2×5+4=14(人).40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)由(1)知,每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
据此解答.
【详解】
(1)2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)5张桌子拼一块,可坐人数:2×5+4=14(人),40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
【点睛】
本题主要考查数与形结合的规律,关键根据所给图形发现这组图形的规律,并运用规律解决问题。
14.(1)5×=5-;作图见详解
(2)100×=100-
【解析】
【分析】
观察可知,第几个等式对应第一个乘数和第二个乘数的分子就是几,分母是分子+1;图形对应规律是第几个等式就将图形平均分成几份,分子是几涂几份。
【详解】
(1)5×=5-;
(2)100×=100-
【点睛】
在探索数与形结合的规律时,要考虑数的排列规律,通过数形结合、对应等方法来解决问题。
答案第1页,共2页
答案第1页,共2页
