24.1.1圆(课件)

课件26张PPT。“一切立体图形中最美的是球，
一切平面图形中最美的是圆”。

————毕达哥拉斯24.1.1 圆圆是一种基本的几何图形，圆形物体在生活中随处可见，例如：生活剪影一石激起千层浪奥运五环福建土楼乐在其中小憩片刻祥子请在白纸上画一个半径为2cm的圆．若要在平坦的操场上画一个半
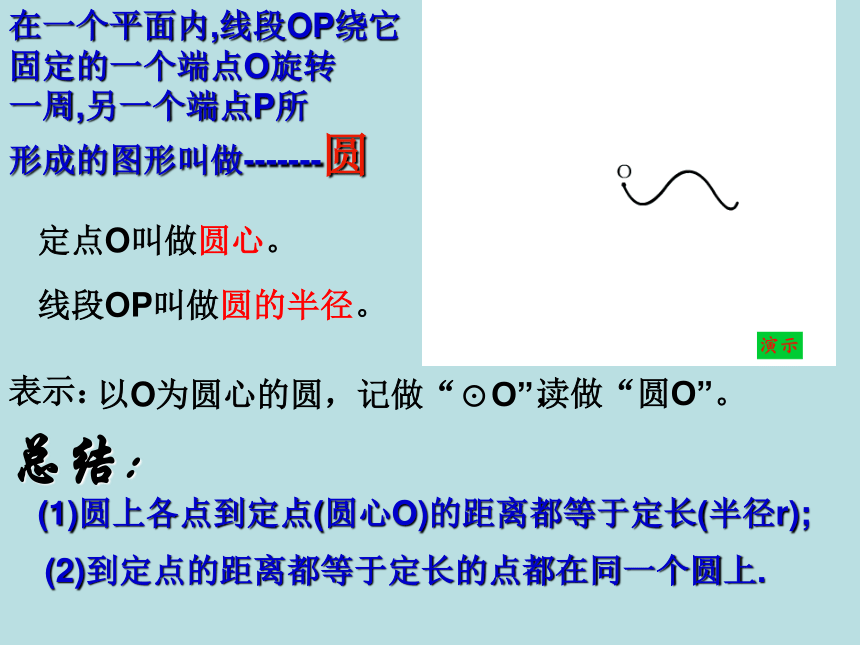
径为3m的圆,你有什么办法?圆的画法定点O叫做圆心。线段OP叫做圆的半径。在一个平面内,线段OP绕它
固定的一个端点O旋转
一周,另一个端点P所
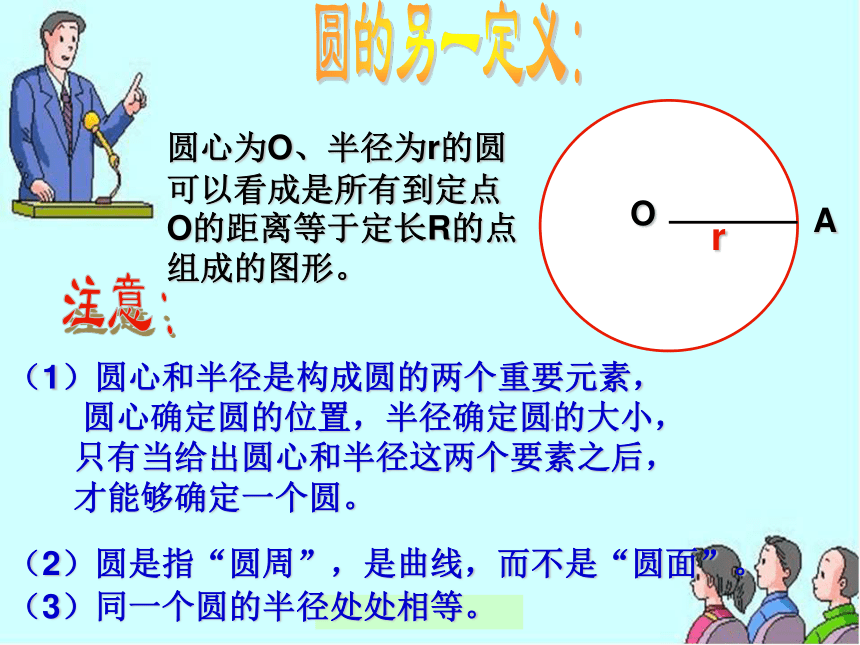
形成的图形叫做-------圆总结:(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);(2)到定点的距离都等于定长的点都在同一个圆上.OA圆的另一定义:r圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长R的点组成的图形。注意：（1）圆心和半径是构成圆的两个重要元素，
圆心确定圆的位置，半径确定圆的大小，
只有当给出圆心和半径这两个要素之后，
才能够确定一个圆。（2）圆是指“圆周”，是曲线，而不是“圆面”。（3）同一个圆的半径处处相等。同心圆 等圆确定一个圆的要素圆心与半径圆心相同，半径不同半径相同，圆心不同生活离不开圆 圆是我们的好朋友圆形车轮为什么平稳? 车轮边缘上任意两点到轴心的距离都相等, 任意一点到轴心的距离是一个定值.圆上的点到圆心的距离是一个定值 投圈游戏 一些学生正在做投圈游戏,他们呈“一”字型排开,这样的队形对每个人公平吗?你认为他们应当排成什么样的队形? 为了使投圈游戏公平,现在有一条3米长的绳子,你准备怎么办?矩形的四个顶点在以对角线交点
为圆心的同一个圆上.
想一想.OABC弦连接圆上任意两点的线段(图中的线段AB、AC）。直径经过圆心的弦（图中的AB）。弦直径注意:凡直径都是弦,是圆中最长的弦,但弦不一定是直径.重要概念(一)即时考你：.OADQCBPHGFE如图(1)直径是_______;

(2)弦是_____________;

(3) PQ是直径吗?______;

(4)线段EF、GH
是弦吗？_______.KABCD、DK、AB不是不是●OBCA 1.如图,半径有:______________OA、OB、OC若∠AOB=60°，
则△AOB是_____三角形. 2.如图,弦有:______________AB、BC、AC在圆中有长度不等的弦，等边直径是圆中最长的弦即时再考你：圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ，读作：“圆弧AB”或“弧AB”。注意：大于半圆的弧（用三个点表示，如： 或 或 ），
叫做优弧；小于半圆的弧叫做劣弧. 如:圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.重要概念(二)●OBCA 1.如图,弧有:______________2 .劣弧有：优弧有：你知道优弧与劣弧的区别么？判断：半圆是弧，但弧不一定是半圆.( )判断下列说法的正误：(1)弦是直径；(2)半圆是弧；(3)过圆心的线段是直径；(6)圆心相同，半径相等的两个圆是同心圆。(4)半圆是最长的弧；(5)直径是最长的弦；
（7）半圆是弧，但弧不一定是半圆.( )
基础训练1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上，图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.A7或312442第5题24°范例例1、如图，点A、B在⊙O上，∠AOB
=60°，试说明△ABO的等边三角形。2、如图，OA、OB、OC是⊙O的三条
半径，∠AOC=∠BOC ，M、N分别是
OA、OB的中点。
求证：MC=NC。巩固范例例2、已知：如图，在⊙O中，A、B是
线段CD于圆的两个交点，且AC=BD。
求证：△OCD为等腰三角形。半径是重要的辅助线6、如图，CD是⊙O的直径，点A在DC
的延长线上，AE交⊙O于点B、E，AB
等于⊙O的半径，∠DOE=78°，求
∠A的度数。巩固课堂小结请谈谈这节课的收获吧 如图,一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 课后拓展(一)正确答案 一个8×10米的长方形草地，现要安装自动喷水装置,这种装置喷水的半径为2.5米,你准备安装几个? 怎样安装? 请说明理由.课后拓展(二)