三角形相似判定二、三
图片预览

文档简介
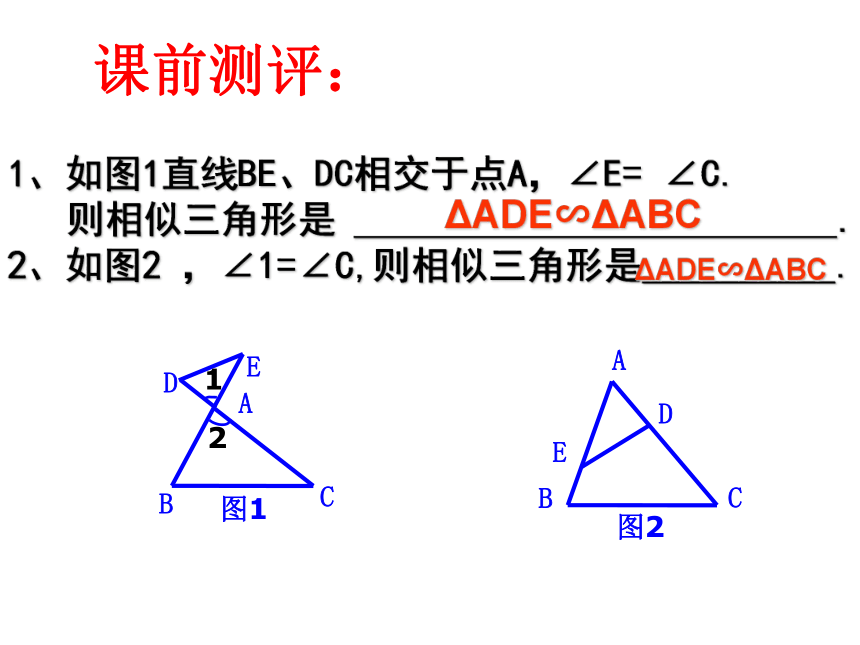
课件13张PPT。1、如图1直线BE、DC相交于点A,∠E= ∠C.
则相似三角形是 .
2、如图2 ,∠1=∠C,则相似三角形是__________.课前测评:ΔADE∽ΔABC
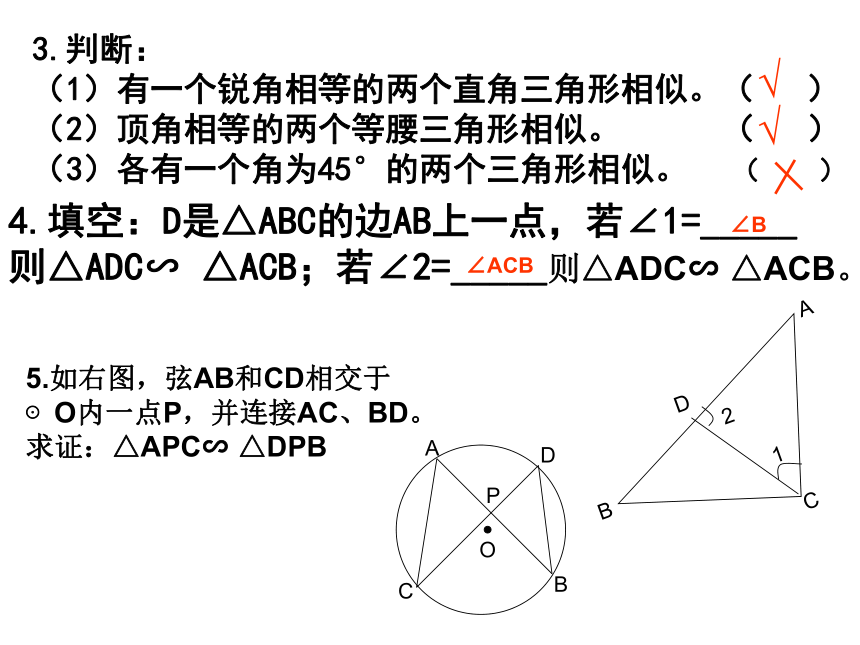
ΔADE∽ΔABC3.判断:
(1)有一个锐角相等的两个直角三角形相似。( )
(2)顶角相等的两个等腰三角形相似。 ( )
(3)各有一个角为45°的两个三角形相似。 ( )4.填空:D是△ABC的边AB上一点,若∠1=_____
则△ADC∽ △ACB;若∠2=_____则△ADC∽ △ACB。
5.如右图,弦AB和CD相交于
⊙O内一点P,并连接AC、BD。
求证:△APC∽ △DPB
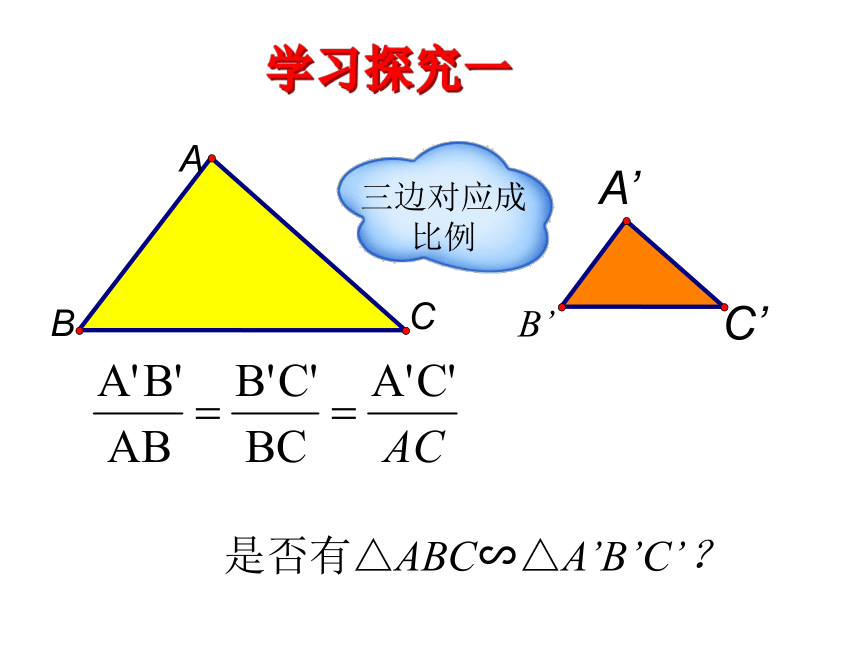
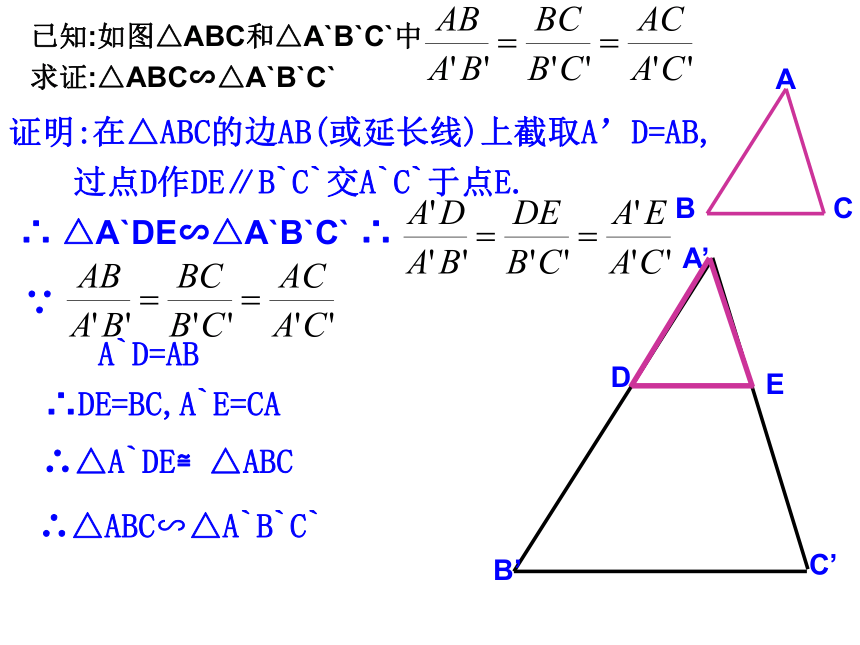
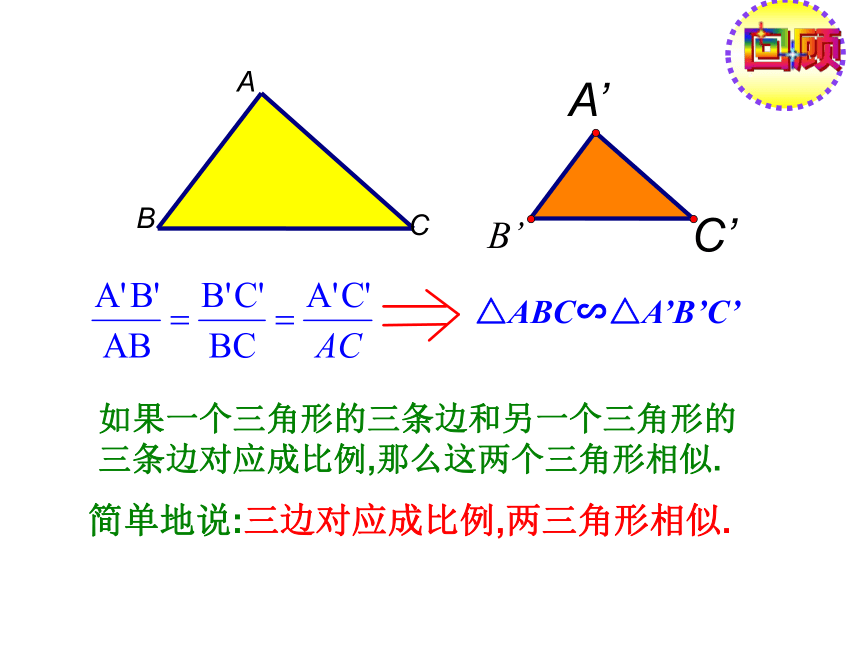
√√∠B∠ACB 是否有△ABC∽△A’B’C’?ABC学习探究一证明:在△ABC的边AB(或延长线)上截取A’D=AB, DE过点D作DE∥B`C`交A`C`于点E. A`D=AB∴DE=BC,A`E=CA∴△ABC∽△A`B`C` ∴△A`DE≌△ABC回顾△ABC∽△A’B’C’ 如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简单地说:三边对应成比例,两三角形相似.练习1:在△ABC和△A′B′C′中,已知:
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
试判定△ABC与A′B′C′是否相似,并说明理由. (2) AB=12cm, BC=15cm, AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=30cm∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 判定定理:如果两个三角形的两组
对应边的比相等,并且相应的夹角相等,
那么这两个三角形相似 (简称:两边夹一角)学习探究二(3)2、判断图中△AEB和△FEC是否相似? 解:∴△AEB∽△FEC ∵∠1=∠212练3.如图:在求证: B△ACP∽△ABC练习.已知:在△ABC中,AB=4,AC=2,P是边AB上一点,连结CP,当PA=___时, BP1△ACP∽△ABC? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似。? 三边对应成比例,两三角形相似.相似三角形的判定方法两组对应边的成相等且相应的夹角相等,
那么 两三角形相似.。? 两角对应相等,两三角形相似.
则相似三角形是 .
2、如图2 ,∠1=∠C,则相似三角形是__________.课前测评:ΔADE∽ΔABC
ΔADE∽ΔABC3.判断:
(1)有一个锐角相等的两个直角三角形相似。( )
(2)顶角相等的两个等腰三角形相似。 ( )
(3)各有一个角为45°的两个三角形相似。 ( )4.填空:D是△ABC的边AB上一点,若∠1=_____
则△ADC∽ △ACB;若∠2=_____则△ADC∽ △ACB。
5.如右图,弦AB和CD相交于
⊙O内一点P,并连接AC、BD。
求证:△APC∽ △DPB
√√∠B∠ACB 是否有△ABC∽△A’B’C’?ABC学习探究一证明:在△ABC的边AB(或延长线)上截取A’D=AB, DE过点D作DE∥B`C`交A`C`于点E. A`D=AB∴DE=BC,A`E=CA∴△ABC∽△A`B`C` ∴△A`DE≌△ABC回顾△ABC∽△A’B’C’ 如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简单地说:三边对应成比例,两三角形相似.练习1:在△ABC和△A′B′C′中,已知:
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
试判定△ABC与A′B′C′是否相似,并说明理由. (2) AB=12cm, BC=15cm, AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=30cm∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 判定定理:如果两个三角形的两组
对应边的比相等,并且相应的夹角相等,
那么这两个三角形相似 (简称:两边夹一角)学习探究二(3)2、判断图中△AEB和△FEC是否相似? 解:∴△AEB∽△FEC ∵∠1=∠212练3.如图:在求证: B△ACP∽△ABC练习.已知:在△ABC中,AB=4,AC=2,P是边AB上一点,连结CP,当PA=___时, BP1△ACP∽△ABC? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似。? 三边对应成比例,两三角形相似.相似三角形的判定方法两组对应边的成相等且相应的夹角相等,
那么 两三角形相似.。? 两角对应相等,两三角形相似.
