2021-2022学年高二下学期数学人教A版(2019) 选择性必修第三册第六章杨辉三角的性质与应用课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019) 选择性必修第三册第六章杨辉三角的性质与应用课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 454.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 08:30:06 | ||
图片预览






文档简介
(共15张PPT)
杨辉三角的性质与应用
第六章 计数原理
目录
知识讲解
知识讲解
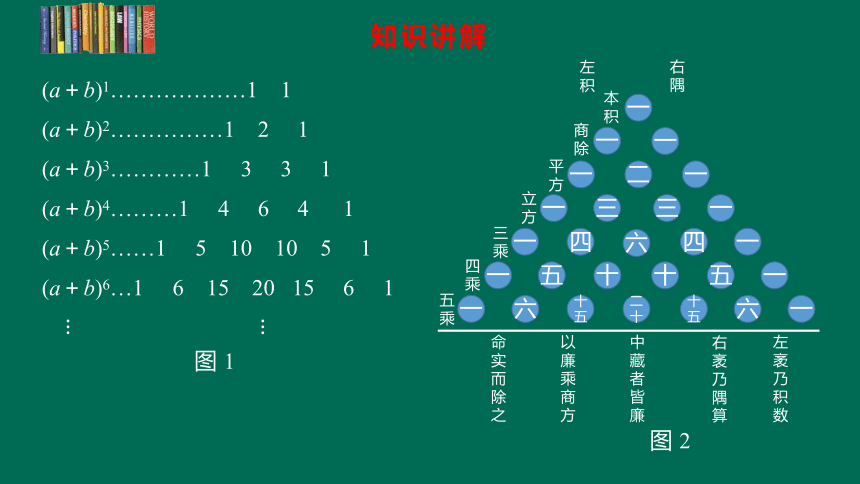
在探究 (a+b)n 的展开式的二项式系数性质时,我们曾把系数写成一张表(图 1),借助它发现了系数的一些规律.事实上,在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书中,就已经出现了这个表.所不同的只是这里的表用阿拉伯数字表示,在那本书里是用汉字表示(图 2).我们称这个表为杨辉三角.
知识讲解
(a+b)1………………1 1
(a+b)2……………1 2 1
(a+b)3…………1 3 3 1
(a+b)4………1 4 6 4 1
(a+b)5……1 5 10 10 5 1
(a+b)6…1 6 15 20 15 6 1
图 1
一
一
一
左积
右隅
二
一
一
三
三
一
一
四
四
六
一
一
五
五
十
十
一
一
六
六
十五
十五
二十
一
一
本积
商除
平方
立方
三乘
四乘
五乘
命实而除之
以廉乘商方
中藏者皆廉
右袤乃隅算
左袤乃积数
图 2
知识讲解
杨辉是我国古代数学史上一位著述丰富的数学家,著有《详解九章算法》《日用算法》和《杨辉算法》.在编写这些算书时,杨辉广泛引用古代数学典籍,使得我们能够了解许多已经失传的数学方法.杨辉在《详解九章算法》里指出,杨辉三角这种方法出于《释锁》算书,且我国北宋数学家贾宪(约11世纪)曾用过.由此可以推断,我国发现这个表不晚于11世纪.在欧洲,这个表被认为是法国数学家帕斯卡(B. Pascal,1623-1662)首先发现的,他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.
杨辉三角本身包含了很多有趣的性质,利用这些性质,可以解决很多数学问题.下面让我们一起来探索吧!
知识讲解
一、探究的内容:杨辉三角的性质与应用
(一)杨辉三角的性质
1.观察杨辉三角的结构,即杨辉三角中数字排列的规律,例如每一行、相邻两行、斜行等,画一画,连一连,算一算,写出你发现的结论.
例如:
(1)结合图 1 和图 2,可以发现,杨辉三角的第 n 行的第 r 个数可以表示为 ,第 n 行就是 (a+b)n 的展开式的二项式系数,如图 3 所示.
知识讲解
第 0 行 1
第 1 行 1 1
第 2 行 1 2 1
第 3 行 1 3 3 1
第 4 行 1 4 6 4 1
第 5 行 1 5 10 10 5 1
第 6 行 1 6 15 20 15 6 1
第 n-1 行 1 1
第 n 行 1 1
图 3
知识讲解
(2)观察杨辉三角的相邻两行,可以发现,三角形的两个腰都是由数字 1 组成的,其余的数都等于它肩上的两个数相加.
如图 4 所示,2=1+1,3=1+2,4=1+3,6=3+3,.一般地,有
=+. ①
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
1
1
5
6
15
20
15
6
1
1
图 4
知识讲解
2.利用已学知识,尝试对所得结论进行证明.
例如,对于①式,可按如下方式进行证明.
因为
+=+=[r+(n-r)]=,
又 =,所以 =+.
上式是杨辉三角最基本的性质,也是二项式系数和组合数的性质.正因为杨辉三角中的数与开方、解方程、组合数学、概率论都有密切的关系,所以历代数学家从不同角度研究它的性质,例如帕斯卡在《论算术三角》一书中就给出了 19 条性质.你也来试一试吧,看能发现和证明多少性质!
知识讲解
(二)杨辉三角的应用
在我国古代,杨辉三角是解决很多数学问题的有力工具,像开方问题、数列问题等.
例如,开方古算题(出自杨辉《详解九章算法》):
积一百三十三万六千三百三十六尺,问为三乘方几何.
在我国清中叶以前,称平方为自乘,立方为再自乘,四次方为三乘方.因此,这个问题相当于解方程 x4=1 336 336.
杨辉三角(图 2)中的五句话,前三句“左袤乃积数,右袤乃隅算,中藏者皆廉”分别说明了图中数字代表的意义,后两句“以廉乘商方,命实而除之”说明了如何应用各行系数进行开方.
知识讲解
你可以查阅相关书籍或上网搜索相关资料,探究一下开方算法的具体操作及其中蕴含的算法思想,感受我国古代数学的独特风格.
再如,数列古算题(出自杨辉《详解九章算法》):
三角垛,下广,一面十二个,上尖,问计几何.
在我国古代,很多数学家研究数列的问题,并取得了辉煌的成就.就像通过研究“三角垛”这样的一类问题——垛积问题,发现了一系列数列的求和公式.上述三角垛问题一般化后,就相当于如下将圆球堆成三角垛的问题:
底层是每边堆 n 个圆球的三角形(如图 5),向上逐层每边减少 1 个,顶层是 1 个,求总数.
图 5
……
……
……
……
知识讲解
利用杨辉三角,就可以解决以上问题,并获得每层圆球数所构成的数列的一般求和公式.你可以试一试.
除此之外,你还可以通过查阅相关书籍或上网搜索相关资料,从杨辉三角出发,一步步探究,拓展到更多类数列的问题.
二、对探究活动的要求
以独立探究和小组合作相结合的方式开展探究活动.建议按如下步骤完成:
1.小组集体讨论探究方案,确定研究思路.
2.小组成员各自开展独立探究,并以专题作业的形式撰写研究报告.
3.小组内进行交流讨论,完善研究成果,并形成一份小组研究报告.
4.全班进行成果交流、评价.
知识讲解
三、研究报告的参考形式
杨辉三角的性质与应用
______年级______班
完成时间:_____________
1.课题组成员及分工
2.发现的数学结论及发现过程概述
知识讲解
3.证明思路及其形成过程描述
4.结论的证明或否定
5.杨辉三角的应用举例
6.收获与体会
谢谢观看
杨辉三角的性质与应用
第六章 计数原理
目录
知识讲解
知识讲解
在探究 (a+b)n 的展开式的二项式系数性质时,我们曾把系数写成一张表(图 1),借助它发现了系数的一些规律.事实上,在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书中,就已经出现了这个表.所不同的只是这里的表用阿拉伯数字表示,在那本书里是用汉字表示(图 2).我们称这个表为杨辉三角.
知识讲解
(a+b)1………………1 1
(a+b)2……………1 2 1
(a+b)3…………1 3 3 1
(a+b)4………1 4 6 4 1
(a+b)5……1 5 10 10 5 1
(a+b)6…1 6 15 20 15 6 1
图 1
一
一
一
左积
右隅
二
一
一
三
三
一
一
四
四
六
一
一
五
五
十
十
一
一
六
六
十五
十五
二十
一
一
本积
商除
平方
立方
三乘
四乘
五乘
命实而除之
以廉乘商方
中藏者皆廉
右袤乃隅算
左袤乃积数
图 2
知识讲解
杨辉是我国古代数学史上一位著述丰富的数学家,著有《详解九章算法》《日用算法》和《杨辉算法》.在编写这些算书时,杨辉广泛引用古代数学典籍,使得我们能够了解许多已经失传的数学方法.杨辉在《详解九章算法》里指出,杨辉三角这种方法出于《释锁》算书,且我国北宋数学家贾宪(约11世纪)曾用过.由此可以推断,我国发现这个表不晚于11世纪.在欧洲,这个表被认为是法国数学家帕斯卡(B. Pascal,1623-1662)首先发现的,他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.
杨辉三角本身包含了很多有趣的性质,利用这些性质,可以解决很多数学问题.下面让我们一起来探索吧!
知识讲解
一、探究的内容:杨辉三角的性质与应用
(一)杨辉三角的性质
1.观察杨辉三角的结构,即杨辉三角中数字排列的规律,例如每一行、相邻两行、斜行等,画一画,连一连,算一算,写出你发现的结论.
例如:
(1)结合图 1 和图 2,可以发现,杨辉三角的第 n 行的第 r 个数可以表示为 ,第 n 行就是 (a+b)n 的展开式的二项式系数,如图 3 所示.
知识讲解
第 0 行 1
第 1 行 1 1
第 2 行 1 2 1
第 3 行 1 3 3 1
第 4 行 1 4 6 4 1
第 5 行 1 5 10 10 5 1
第 6 行 1 6 15 20 15 6 1
第 n-1 行 1 1
第 n 行 1 1
图 3
知识讲解
(2)观察杨辉三角的相邻两行,可以发现,三角形的两个腰都是由数字 1 组成的,其余的数都等于它肩上的两个数相加.
如图 4 所示,2=1+1,3=1+2,4=1+3,6=3+3,.一般地,有
=+. ①
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
1
1
5
6
15
20
15
6
1
1
图 4
知识讲解
2.利用已学知识,尝试对所得结论进行证明.
例如,对于①式,可按如下方式进行证明.
因为
+=+=[r+(n-r)]=,
又 =,所以 =+.
上式是杨辉三角最基本的性质,也是二项式系数和组合数的性质.正因为杨辉三角中的数与开方、解方程、组合数学、概率论都有密切的关系,所以历代数学家从不同角度研究它的性质,例如帕斯卡在《论算术三角》一书中就给出了 19 条性质.你也来试一试吧,看能发现和证明多少性质!
知识讲解
(二)杨辉三角的应用
在我国古代,杨辉三角是解决很多数学问题的有力工具,像开方问题、数列问题等.
例如,开方古算题(出自杨辉《详解九章算法》):
积一百三十三万六千三百三十六尺,问为三乘方几何.
在我国清中叶以前,称平方为自乘,立方为再自乘,四次方为三乘方.因此,这个问题相当于解方程 x4=1 336 336.
杨辉三角(图 2)中的五句话,前三句“左袤乃积数,右袤乃隅算,中藏者皆廉”分别说明了图中数字代表的意义,后两句“以廉乘商方,命实而除之”说明了如何应用各行系数进行开方.
知识讲解
你可以查阅相关书籍或上网搜索相关资料,探究一下开方算法的具体操作及其中蕴含的算法思想,感受我国古代数学的独特风格.
再如,数列古算题(出自杨辉《详解九章算法》):
三角垛,下广,一面十二个,上尖,问计几何.
在我国古代,很多数学家研究数列的问题,并取得了辉煌的成就.就像通过研究“三角垛”这样的一类问题——垛积问题,发现了一系列数列的求和公式.上述三角垛问题一般化后,就相当于如下将圆球堆成三角垛的问题:
底层是每边堆 n 个圆球的三角形(如图 5),向上逐层每边减少 1 个,顶层是 1 个,求总数.
图 5
……
……
……
……
知识讲解
利用杨辉三角,就可以解决以上问题,并获得每层圆球数所构成的数列的一般求和公式.你可以试一试.
除此之外,你还可以通过查阅相关书籍或上网搜索相关资料,从杨辉三角出发,一步步探究,拓展到更多类数列的问题.
二、对探究活动的要求
以独立探究和小组合作相结合的方式开展探究活动.建议按如下步骤完成:
1.小组集体讨论探究方案,确定研究思路.
2.小组成员各自开展独立探究,并以专题作业的形式撰写研究报告.
3.小组内进行交流讨论,完善研究成果,并形成一份小组研究报告.
4.全班进行成果交流、评价.
知识讲解
三、研究报告的参考形式
杨辉三角的性质与应用
______年级______班
完成时间:_____________
1.课题组成员及分工
2.发现的数学结论及发现过程概述
知识讲解
3.证明思路及其形成过程描述
4.结论的证明或否定
5.杨辉三角的应用举例
6.收获与体会
谢谢观看
