第20章数据的分析练习题2020-2021学年宁夏部分地区人教版数学八年级下学期期末试题选编(Word版含解析)
文档属性
| 名称 | 第20章数据的分析练习题2020-2021学年宁夏部分地区人教版数学八年级下学期期末试题选编(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 10:21:02 | ||
图片预览



文档简介
第20章:数据的分析练习题
一、单选题
1.(2021·宁夏原州·八年级期末)服装销售商在进行市场占有情况的调查时,最应该关注的是已售出服装型号的( )
A.中位数 B.平均数 C.众数 D.最小数
2.(2021·宁夏大武口·八年级期末)某次疫情知识竞赛8名选手得分如下表:
得分 80 85 87 90
人数 1 3 2 2
则这8名选手得分的众数,中位数分别是( )
A.85、86 B.87、85 C.85、85 D.85、87
3.(2021·宁夏同心·八年级期末)2021年4月23日是第25个世界读书日,某中学为了解九年级学生假期的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下
册数/册 1 2 3 4 5
人数/人 1 6 7 3 3
根据统计表中的数据,这20名同学读书册数的众数是( )
A.7 B.6 C.3 D.2
4.(2021·宁夏同心·八年级期末)为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如下统计图(每个小组含前一个边界值,不含后一个边界值),根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A.中位数在60分~70分之间 B.中位数在70分~80分之间
C.中位数在80分~90分之间 D.中位数在90分~100分之间
5.(2021·宁夏红寺堡·八年级期末)期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”.上面两位同学的话能反映出的统计量分别是( )
A.众数和平均数 B.平均数和中位数
C.众数和方差 D.众数和中位数
6.(2021·宁夏原州·八年级期末)小明在参加区运动会前刻苦进行100米跑训练,老师对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则老师需要知道他这10次成绩的( )
A.众数 B.方差 C.平均数 D.频数
7.(2021·宁夏西吉·八年级期末)甲、乙、丙、丁四位同学的五次数学测验成绩统计如下表所示,如果要从这四位同学中,选出一位成绩好又稳定的同学参加数学竞赛,则应选的同学是( )
甲 乙 丙 丁
平均分 90 85 90 85
方差 42 50 50 42
A.甲 B.乙 C.丙 D.丁
二、填空题
8.(2021·宁夏同心·八年级期末)甲、乙两个样本,甲的方差为0.102,乙的方差为0.06,哪个样本的数据波动大?答:________.
9.(2021·宁夏同心·八年级期末)如果一组数据4,x,2,3,6的平均数是4,那么x是_____.
10.(2021·宁夏·银川市第十八中学八年级期末)某校组织了一次比赛,甲、乙两队各有5人参加比赛,两队每人的比赛成绩(单位:分)如下:
甲队:7,8,9,6,10
乙队:10,9,5,8,8
已知甲队成绩的方差为S甲2=2,则成绩波动较大的是_____队.
11.(2021·宁夏大武口·八年级期末)已知一组数据:1, 2,2, 2, 3,则这组数据的方差是_______.
12.(2021·宁夏原州·八年级期末)、、三种糖果售价分别为每千克10元,11元,14元.若将种糖果3kg,种糖果2kg,种糖果1kg混在一起,则售价应定为每千克______元.
13.(2021·宁夏红寺堡·八年级期末)某中学八年级人数相等的甲、乙两个班级参加了同一次数学测验,两班平均分和方差分别为甲=79分,乙=79分,S甲 =235,S乙 =201,则成绩较为整齐的是______(填“甲班”或“乙班”).
14.(2021·宁夏西吉·八年级期末)在一组数据中,出现次数最多的数据叫做这组数据的________.
15.(2021·宁夏·平罗县教学研究室(平罗县教师发展中心)八年级期末)某快餐店某天销售3种盒饭的有关数据如图所示,则3种盒饭的价格平均数是_____元.
16.(2021·宁夏·平罗县教学研究室(平罗县教师发展中心)八年级期末)某生物学习小组进行了“亲手发豆芽感受新生长”的生物实践活动,在《种子萌发及生长》项目学习报告中,记录了颗黄豆芽在生芽第三天时的长度如表:
黄豆芽的长度/
对应黄豆发芽的数量/颗
则黄豆芽长度的中位数为___________.
三、解答题
17.(2021·宁夏红寺堡·八年级期末)某公司为了了解员工每人所创年利润情况,公司从各部门抽取部分员工对每年所创年利润情况进行统计,并绘制如图所示的统计图.
(1)求抽取员工总人数,并将图补充完整;
(2)每人所创年利润的众数是________,每人所创年利润的中位数是________,平均数是________;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
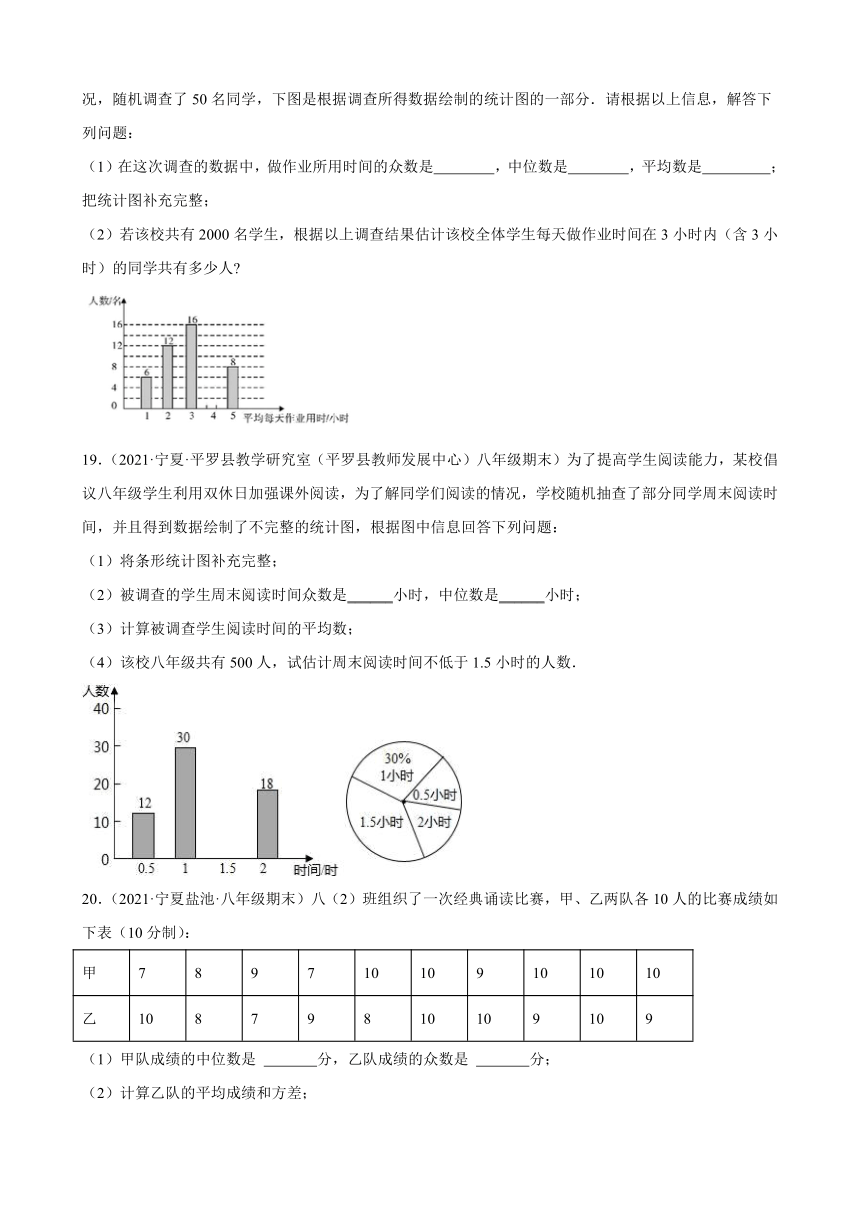
18.(2021·宁夏·银川市第十八中学八年级期末)某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是 ,中位数是 ,平均数是 ;把统计图补充完整;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人
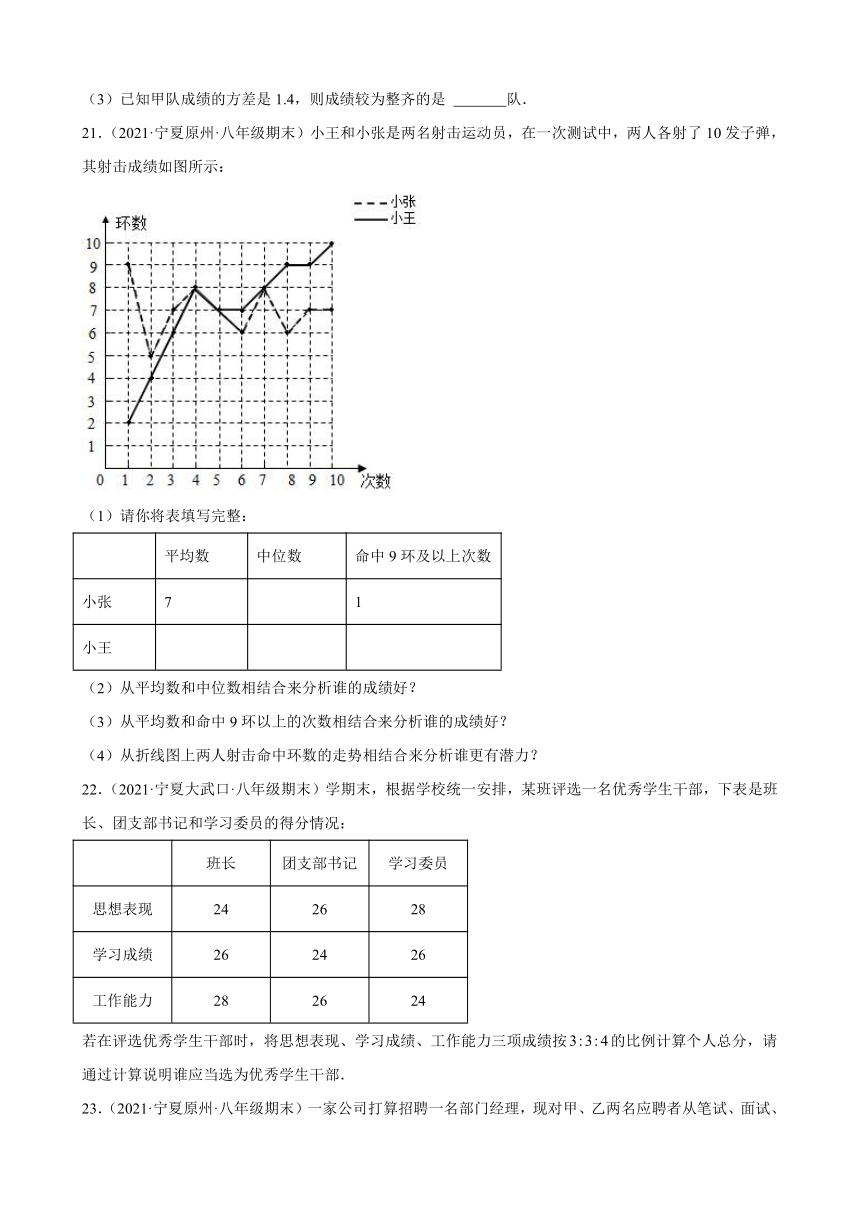
19.(2021·宁夏·平罗县教学研究室(平罗县教师发展中心)八年级期末)为了提高学生阅读能力,某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)被调查的学生周末阅读时间众数是______小时,中位数是______小时;
(3)计算被调查学生阅读时间的平均数;
(4)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
20.(2021·宁夏盐池·八年级期末)八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
21.(2021·宁夏原州·八年级期末)小王和小张是两名射击运动员,在一次测试中,两人各射了10发子弹,其射击成绩如图所示:
(1)请你将表填写完整:
平均数 中位数 命中9环及以上次数
小张 7 1
小王
(2)从平均数和中位数相结合来分析谁的成绩好?
(3)从平均数和命中9环以上的次数相结合来分析谁的成绩好?
(4)从折线图上两人射击命中环数的走势相结合来分析谁更有潜力?
22.(2021·宁夏大武口·八年级期末)学期末,根据学校统一安排,某班评选一名优秀学生干部,下表是班长、团支部书记和学习委员的得分情况:
班长 团支部书记 学习委员
思想表现 24 26 28
学习成绩 26 24 26
工作能力 28 26 24
若在评选优秀学生干部时,将思想表现、学习成绩、工作能力三项成绩按的比例计算个人总分,请通过计算说明谁应当选为优秀学生干部.
23.(2021·宁夏原州·八年级期末)一家公司打算招聘一名部门经理,现对甲、乙两名应聘者从笔试、面试、实习三个方面表现进行评分,甲、乙两名应聘者的各项成绩如表所示:
应聘者 笔试成绩 面试成绩 实习成绩
甲 85 83 90
乙 80 85 92
若笔试、面试、实习成绩按的比确定,会录用哪位应聘者,为什么?
24.(2021·宁夏同心·八年级期末)“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩如图所示.
(1)请你计两个班的平均成绩各是多少分;
(2)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
25.(2021·宁夏西吉·八年级期末)某校开展“卫生西吉100问”知识竞赛,八年级两个班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手复赛成绩如图所示.
班级 平均数(分) 中位数 众数
八(A)班 85 85
八(B)班 80
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
26.(2021·宁夏同心·八年级期末)2020年12月17日凌晨,嫦娥五号返回器携带月球样品在内蒙古四子王旗预定区域安全着陆,标志着我国首次地外采样返回任务圆满完成.某校以此为契机,组织了“中国梦 航天情”系列活动.下面是八年级甲、乙两个班各项目的成绩(单位:分)
项目/班次 知识竞赛 演讲比赛 版面创作
甲 85 91 88
乙 90 84 87
如果将知识竞赛、演讲比赛、版面创作按5:3:2的比例确定最后成绩,请通过计算说明甲乙两班谁将获胜.
试卷第1页,共3页
参考答案:
1.C
【分析】
他们应该最关注的是哪种服装售出的最多,因而最关心的是众数.
【详解】
解:服装销售商在进行市场占有情况的调查时,他们应该最关注的是哪种服装售出的最多,因而最关心的是众数.
故选:C.
【点睛】
本题主要考查统计的有关知识,主要包括平均数、中位数、众数的意义,解题的关键是掌握反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
2.A
【分析】
由表可知,得分80的有1人,得分85的有3人,得分87的有2人,得分90的有2人.再根据众数和平均数概念求解;
【详解】
解:众数是一组数据中出现次数最多的数据,
∴众数是85;
把数据按从小到大顺序排列,可得中位数=(85+87)÷2=86;
故选:A.
【点睛】
本题考查了众数和中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个,找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.
3.C
【分析】
根据众数的定义分别进行解答即可.
【详解】
解:∵3出现了7次,出现的次数最多,
∴这组数据的众数是3册.
故选:C.
【点睛】
本题考查了众数的定义.用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.
4.C
【分析】
根据统计图得出参赛学生的总人数,根据中位数的定义计算即可得答案.
【详解】
∵参赛学生的总人数为30+60+90+90=270(人),
∴这次知识竞赛成绩的中位数为从低到高排列的第135、136位的平均数,
∴这次知识竞赛成绩的中位数在80分~90分之间,
故选:C.
【点睛】
本题考查中位数,熟练掌握中位数的定义及计算方法是解题关键.
5.D
【分析】
根据众数和中位数的概念可得出结论.
【详解】
一组数据中出现次数最多的数值是众数;将数据从小到大排列,当项数为奇数时中间的数为中位数,当项数为偶数时中间两个数的平均数为中位数;由题可知,小明所说的是多数人的分数,是众数,小英所说的为排在中间人的分数,是中位数.
故选为D.
【点睛】
本题考查众数和中位数的定义,熟记定义是解题的关键.
6.B
【详解】
分析:根据众数、平均数、频数、方差的概念分析.
详解:众数、平均数是反映一组数据的集中趋势,而频数是数据出现的次数,只有方差是反映数据的波动大小的.故为了判断成绩是否稳定,需要知道的是方差.
故选B.
点睛:此题考查统计学的相关知识.注意:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.A
【分析】
先找到四人中平均数大的,即成绩好的;再从平均成绩好的人中选择方差小,即成绩稳定的,从而得出答案.
【详解】
解:∵,
∴四位同学中甲、丙的平均成绩较好,
又∵S甲2<S丙2,
∴甲的成绩好又稳定,
故选:A.
【点睛】
本题考查平均数和方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
8.甲的波动比乙的波动大.
【分析】
根据方差的定义,方差越小数据越稳定,故可得到正确答案.
【详解】
解:根据方差的意义,甲样本的方差大于乙样本的方差,故甲的波动比乙的波动大.
故答案:甲的波动比乙的波动大.
【点睛】
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
9.
【分析】
由一组数据4,x,2,3,6的平均数是4,可列方程:再解方程可得答案.
【详解】
解: 一组数据4,x,2,3,6的平均数是4,
故答案为:
【点睛】
本题考查的是平均数的含义,掌握平均数的计算是解题的关键.
10.乙
【分析】
先由平均数的公式计算出乙队的平均成绩,再根据方差的公式求出乙队的方差,然后根据方差的意义即可得出答案.
【详解】
解:乙队的平均成绩为(10+9+5+8+8)=8(分),
其方差S2乙=[(10﹣8)2+(9﹣8)2+(5﹣8)2+(8﹣8)2+(8﹣8)2]=2.8.
∵22.8,即S2甲S2乙,
∴乙队成绩波动较大.
故答案为:乙.
【点睛】
本题主要考查平均数与方差,掌握平均数与方差的求法是解题的关键.
11.0.4
【分析】
先由平均数的公式计算出这组数据的平均数,再根据方差的公式进行计算即可.
【详解】
这组数据的平均数是(1+2+2+2+3)÷5=2
则这组数据的方差是:
故答案为:0.4.
【点睛】
本题考查了求方差,熟记公式是解题关键.
12.11
【分析】
根据加权平均数的计算方法是求出所有糖果的总钱数,然后除以糖果的总质量.
【详解】
解:售价应定为每千克(元.
故答案为:11.
【点睛】
本题考查的是加权平均数的求法,本题易出现的错误是对加权平均数的理解不正确,而求10、11、14这三个数的平均数.
13.乙班
【分析】
根据方差的意义(方差越小数据越稳定)进行判断.
【详解】
解:因为S甲 =235,S乙 =201,
则乙的方差小于甲的方差,
所以成绩较为整齐的是乙班.
故答案为:乙班.
【点睛】
本题考查了方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
14.众数
【详解】
本题考查的是众数的定义
根据众数的定义即可解答.
一组数据中出现次数最多的数据就是这组数据的众数.
15.8.7
【分析】
根据扇形统计图获取信息,利用加权平均数的定义列式计算即可.
【详解】
解:3种盒饭的价格平均数是6×25%+8×15%+10×60%=8.7(元),
故答案为:8.7.
【点睛】
本题考查获取扇形统计图信息,加权平均数,掌握获取扇形统计图信息,加权平均数,会利用加权平均数解决问题是关键.
16.15.5
【分析】
中位数是将一组数据按照大小顺序排列后,取最中间或最中间两个数的平均数,根据中位数的定义即可得出答案.
【详解】
解:将这30颗黄豆芽的长度排序后,第15,16个数据分别为15mm,16mm,
所以中位数为: (mm),
故答案为:15.5.
【点睛】
本题主要考查了中位数的定义,解决本题的关键是要熟练掌握中位数的定义.
17.(1)见解析(2)8万元,8万元,8.12万元(3)384人
【分析】
试题分析:(1)根据扇形中各部分所占的百分比的和是1,即可求得3万元的员工所占的百分比,然后根据百分比的意义求得直方图中缺少部分的人数;
(2)根据众数、中位数以及平均数的定义求解;
(3)利用总数1200乘以对应的比例即可求解.
【详解】
试题解析:(1)3万元的员工的百分比为:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取员工总数为:4÷8%=50(人)
5万元的员工人数为:50×24%=12(人)
8万元的员工人数为:50×36%=18(人)
(2)每人所创年利润的众数是 8万元,每人所创年利润的中位数是8万元,
平均数是:(3×4+5×12+8×18+10×10+15×6)=8.12万元.
故答案为8万元,8万元,8.12万元.
(3)1200×=384(人).
答:在公司1200员工中有384人可以评为优秀员工.
【点睛】
考点: 条形统计图;用样本估计总体;扇形统计图;加权平均数;中位数.
18.(1)3小时,3小时,3小时,补图见解析;(2)1360人
【分析】
(1)首先求得平均每天作业用时是4小时的人数,然后利用众数,中位数,平均数的定义即可求解;
(2)利用总人数2000乘以每天做作业时间在3小时内(含3小时)的同学所占的比例即可求解.
【详解】
(1)每天作业用时是4小时的人数是:50-6-12-16-8=8(人),
∵每天作业用时是3小时的人数最多,是16人,
∴众数是3小时;
∵从小到大排列后排在第25和第26位的都是每天作业用时是3小时的人,
∴中位数是3小时;
平均数是(小时),
补全条形统计图如图所示:
故答案为:3小时、3小时、3小时;
(3)2000×(人),
答:估计该校全体学生每天组作业时间在3小时内(含3小时)的同学共有1360人.
【点睛】
本题考查了平均数、中位数、众数的意义和计算方法,掌握平均数、中位数、众数的计算方法是正确计算的前提,样本估计总体是统计中常用的方法.
19.(1)补图见解析;(2)1.5,1.5;(3)被调查同学的平均阅读时间为1.32小时;(4)290人.
【分析】
(1)由条形图知,周末阅读1小时的有30人,由扇形图可知,周末阅读1小时的人数占总人数的30%,将30除以30%先解得总人数,再减去各项人数即可解题;
(2)众数是一组数据中出现最多次的数,中位数是将这组数据按顺序排列,位于正中间的一个数(或正中间的两个数的平均值),据此解题;
(3)将计算各时间段阅读的时间总和除以100即可;
(4)先周末阅读时间不低于1.5小时的人数占总人数的比例,再乘以500即可解题.
【详解】
解:(1)由题意可得,本次调查的学生数为:30÷30%=100(人),
阅读时间1.5小时的学生数为:100﹣12﹣30﹣18=40(人),
补全的条形统计图如图所示,
(2)由补全的条形统计图可知,有40人周末阅读时间在1.5小时,其他时间段的人数都比40少,即被调查的学生周末阅读时间众数是1.5小时;
总共调查100个数据,位于正中间的数是第50个与第51个数,即中位数是1.5小时,
故答案为:1.5,1.5;
(3)所有被调查学生阅读时间的平均数为:×(12×0.5+30×1+40×1.5+18×2)=1.32小时,即所有被调查同学的平均阅读时间为1.32小时;
(4)估计周末阅读时间不低于1.5小时的人数为500×=290(人).
【点睛】
本题考查条形统计图与扇形统计图,涉及众数、中位数、平均数、用样本估计总体等知识,是重要考点,难度较易,掌握相关知识是解题关键.
20.(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【分析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【详解】
解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
【点睛】
本题考查方差、中位数和众数:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
21.(1)7,7,7.5,3;(2)小王的成绩比较好;(3)小王的成绩比较好;(4)小王更有潜力
【分析】
(1)根据中位数,平均数的定义求解即可;
(2)从平均数和中位数相结合来分析可得结论;
(3)从平均数和命中9环以上的次数相结合来分析可得结论;
(4)从折线图上两人射击命中环数的走势分析可得结论.
【详解】
解:(1)小张的中位数为7,
小王的平均数,
小王的中位数,
小王命中9环及以上次数为3.
故答案为:7,7,7.5,3.
(2)从平均数看两人的成绩一样,
从中位数来看小王的成绩比较好.
综上所述,小王的成绩比较好.
(3)从平均数和命中9环以上的次数相结合来看,小王的成绩比较好.
(4)从折线图上两人射击命中环数的走势相结合来看,小王更有潜力.
【点睛】
本题考查折线统计图,中位数,平均数等知识,解题的关键是理解中位数,平均数的定义,属于中考常考题型.
22.班长应当选
【分析】
根据三项成绩的不同权重,分别计算三人的成绩.
【详解】
解:班长的成绩==26.2(分),
学习委员的成绩==25.8(分),
团支部书记的成绩==25.4(分),
∵26.2>25.8>25.4,
∴班长应当选.
【点睛】
本题考查了加权成绩的计算.解题的关键是掌握加权平均数的定义.
23.乙,理由见解析
【分析】
首先根据加权平均数的计算方法,分别求出甲、乙的平均成绩各是多少;然后比较大小,判断出谁会被公司录取即可.
【详解】
解:甲的平均成绩为:(分,
乙的平均成绩为:(分,
,
乙的平均成绩较高,
乙会被公司录取.
【点睛】
本题考查了加权平均数的知识,解题的关键是牢记公式并正确的运算.
24.(1)86分,86分;(2)八(1)班的成绩较为整齐
【分析】
(1)根据每个班5名学生的成绩,求出对应班级的平均成绩即可得到答案;
(2)根据(1)中求得的每个班级的平均成绩,求出对应的方差,然后判断即可得到答案.
【详解】
解:(1)由条形分布图可知:
八(1)班的5名学生的成绩分别为:80、80、90、80、100
八(2)班的5名学生的成绩分别为:80、100、95、70、85
∴八(1)班的5名学生的平均成绩(分)
八(2)班的5名学生的平均成绩(分)
答:两个班的平均成绩各是86分、86分;
(2)八(1)班的5名学生成绩的方差
八(2)班的5名学生成绩的方差
∴八(1)班的5名学生成绩的方差小于八(2)班的5名学生成绩的方差
∴八(1)班的成绩较为整齐.
【点睛】
本题主要考查了平均数和方差,并用方差比较稳定性,解题的关键在于能够熟练掌握相关知识进行求解.
25.(1)85,85,100;(2)八(A)班成绩好些.因为两个班的平均数一样,八(A)班的中位数高,所以八(A)班成绩好些.
【分析】
(1)观察统计图分别写出八(A)班和八(B)班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
(2)在平均数相同的情况下,中位数高的成绩较好.
【详解】
解:(1)由图可知八(A)班5名选手的复赛成绩为:75、80、85、85、100,
八(B)班5名选手的复赛成绩为:70、100、100、75、80,
八(A)的平均数为(75+80+85+85+100)÷5=85,
八(A)的中位数为85,
八(A)的众数为85,
把八(B)的成绩按从小到大的顺序排列为:70、75、80、100、100,
八(B)班的中位数是80;
八(B)班的众数是100;
八(B)的平均数为(70+75+80+100+100)÷5=85,
故答案是:85,85,100;
(2)八(A)班成绩好些.因为两个班的平均数一样,八(A)班的中位数高,所以八(A)班成绩好些.
【点睛】
本题考查了中位数、众数以及平均数的求法,并用这些统计量进行决策,解题的关键是牢记这些统计量的意义,并能熟练运用计算公式.
26.乙班将获胜
【分析】
根据加权平均数的计算公式带入求平均数即可;
【详解】
解:甲班平均成绩: (分),
乙班的平均成绩: (分),
∵ ,
∴乙班将获胜.
【点睛】
此题考查利用加权平均数做决策,考查加权平均数的计算,难度一般.
答案第1页,共2页
一、单选题
1.(2021·宁夏原州·八年级期末)服装销售商在进行市场占有情况的调查时,最应该关注的是已售出服装型号的( )
A.中位数 B.平均数 C.众数 D.最小数
2.(2021·宁夏大武口·八年级期末)某次疫情知识竞赛8名选手得分如下表:
得分 80 85 87 90
人数 1 3 2 2
则这8名选手得分的众数,中位数分别是( )
A.85、86 B.87、85 C.85、85 D.85、87
3.(2021·宁夏同心·八年级期末)2021年4月23日是第25个世界读书日,某中学为了解九年级学生假期的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下
册数/册 1 2 3 4 5
人数/人 1 6 7 3 3
根据统计表中的数据,这20名同学读书册数的众数是( )
A.7 B.6 C.3 D.2
4.(2021·宁夏同心·八年级期末)为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如下统计图(每个小组含前一个边界值,不含后一个边界值),根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A.中位数在60分~70分之间 B.中位数在70分~80分之间
C.中位数在80分~90分之间 D.中位数在90分~100分之间
5.(2021·宁夏红寺堡·八年级期末)期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”.上面两位同学的话能反映出的统计量分别是( )
A.众数和平均数 B.平均数和中位数
C.众数和方差 D.众数和中位数
6.(2021·宁夏原州·八年级期末)小明在参加区运动会前刻苦进行100米跑训练,老师对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则老师需要知道他这10次成绩的( )
A.众数 B.方差 C.平均数 D.频数
7.(2021·宁夏西吉·八年级期末)甲、乙、丙、丁四位同学的五次数学测验成绩统计如下表所示,如果要从这四位同学中,选出一位成绩好又稳定的同学参加数学竞赛,则应选的同学是( )
甲 乙 丙 丁
平均分 90 85 90 85
方差 42 50 50 42
A.甲 B.乙 C.丙 D.丁
二、填空题
8.(2021·宁夏同心·八年级期末)甲、乙两个样本,甲的方差为0.102,乙的方差为0.06,哪个样本的数据波动大?答:________.
9.(2021·宁夏同心·八年级期末)如果一组数据4,x,2,3,6的平均数是4,那么x是_____.
10.(2021·宁夏·银川市第十八中学八年级期末)某校组织了一次比赛,甲、乙两队各有5人参加比赛,两队每人的比赛成绩(单位:分)如下:
甲队:7,8,9,6,10
乙队:10,9,5,8,8
已知甲队成绩的方差为S甲2=2,则成绩波动较大的是_____队.
11.(2021·宁夏大武口·八年级期末)已知一组数据:1, 2,2, 2, 3,则这组数据的方差是_______.
12.(2021·宁夏原州·八年级期末)、、三种糖果售价分别为每千克10元,11元,14元.若将种糖果3kg,种糖果2kg,种糖果1kg混在一起,则售价应定为每千克______元.
13.(2021·宁夏红寺堡·八年级期末)某中学八年级人数相等的甲、乙两个班级参加了同一次数学测验,两班平均分和方差分别为甲=79分,乙=79分,S甲 =235,S乙 =201,则成绩较为整齐的是______(填“甲班”或“乙班”).
14.(2021·宁夏西吉·八年级期末)在一组数据中,出现次数最多的数据叫做这组数据的________.
15.(2021·宁夏·平罗县教学研究室(平罗县教师发展中心)八年级期末)某快餐店某天销售3种盒饭的有关数据如图所示,则3种盒饭的价格平均数是_____元.
16.(2021·宁夏·平罗县教学研究室(平罗县教师发展中心)八年级期末)某生物学习小组进行了“亲手发豆芽感受新生长”的生物实践活动,在《种子萌发及生长》项目学习报告中,记录了颗黄豆芽在生芽第三天时的长度如表:
黄豆芽的长度/
对应黄豆发芽的数量/颗
则黄豆芽长度的中位数为___________.
三、解答题
17.(2021·宁夏红寺堡·八年级期末)某公司为了了解员工每人所创年利润情况,公司从各部门抽取部分员工对每年所创年利润情况进行统计,并绘制如图所示的统计图.
(1)求抽取员工总人数,并将图补充完整;
(2)每人所创年利润的众数是________,每人所创年利润的中位数是________,平均数是________;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
18.(2021·宁夏·银川市第十八中学八年级期末)某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是 ,中位数是 ,平均数是 ;把统计图补充完整;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人
19.(2021·宁夏·平罗县教学研究室(平罗县教师发展中心)八年级期末)为了提高学生阅读能力,某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)被调查的学生周末阅读时间众数是______小时,中位数是______小时;
(3)计算被调查学生阅读时间的平均数;
(4)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
20.(2021·宁夏盐池·八年级期末)八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
21.(2021·宁夏原州·八年级期末)小王和小张是两名射击运动员,在一次测试中,两人各射了10发子弹,其射击成绩如图所示:
(1)请你将表填写完整:
平均数 中位数 命中9环及以上次数
小张 7 1
小王
(2)从平均数和中位数相结合来分析谁的成绩好?
(3)从平均数和命中9环以上的次数相结合来分析谁的成绩好?
(4)从折线图上两人射击命中环数的走势相结合来分析谁更有潜力?
22.(2021·宁夏大武口·八年级期末)学期末,根据学校统一安排,某班评选一名优秀学生干部,下表是班长、团支部书记和学习委员的得分情况:
班长 团支部书记 学习委员
思想表现 24 26 28
学习成绩 26 24 26
工作能力 28 26 24
若在评选优秀学生干部时,将思想表现、学习成绩、工作能力三项成绩按的比例计算个人总分,请通过计算说明谁应当选为优秀学生干部.
23.(2021·宁夏原州·八年级期末)一家公司打算招聘一名部门经理,现对甲、乙两名应聘者从笔试、面试、实习三个方面表现进行评分,甲、乙两名应聘者的各项成绩如表所示:
应聘者 笔试成绩 面试成绩 实习成绩
甲 85 83 90
乙 80 85 92
若笔试、面试、实习成绩按的比确定,会录用哪位应聘者,为什么?
24.(2021·宁夏同心·八年级期末)“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩如图所示.
(1)请你计两个班的平均成绩各是多少分;
(2)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
25.(2021·宁夏西吉·八年级期末)某校开展“卫生西吉100问”知识竞赛,八年级两个班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手复赛成绩如图所示.
班级 平均数(分) 中位数 众数
八(A)班 85 85
八(B)班 80
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
26.(2021·宁夏同心·八年级期末)2020年12月17日凌晨,嫦娥五号返回器携带月球样品在内蒙古四子王旗预定区域安全着陆,标志着我国首次地外采样返回任务圆满完成.某校以此为契机,组织了“中国梦 航天情”系列活动.下面是八年级甲、乙两个班各项目的成绩(单位:分)
项目/班次 知识竞赛 演讲比赛 版面创作
甲 85 91 88
乙 90 84 87
如果将知识竞赛、演讲比赛、版面创作按5:3:2的比例确定最后成绩,请通过计算说明甲乙两班谁将获胜.
试卷第1页,共3页
参考答案:
1.C
【分析】
他们应该最关注的是哪种服装售出的最多,因而最关心的是众数.
【详解】
解:服装销售商在进行市场占有情况的调查时,他们应该最关注的是哪种服装售出的最多,因而最关心的是众数.
故选:C.
【点睛】
本题主要考查统计的有关知识,主要包括平均数、中位数、众数的意义,解题的关键是掌握反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
2.A
【分析】
由表可知,得分80的有1人,得分85的有3人,得分87的有2人,得分90的有2人.再根据众数和平均数概念求解;
【详解】
解:众数是一组数据中出现次数最多的数据,
∴众数是85;
把数据按从小到大顺序排列,可得中位数=(85+87)÷2=86;
故选:A.
【点睛】
本题考查了众数和中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个,找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.
3.C
【分析】
根据众数的定义分别进行解答即可.
【详解】
解:∵3出现了7次,出现的次数最多,
∴这组数据的众数是3册.
故选:C.
【点睛】
本题考查了众数的定义.用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.
4.C
【分析】
根据统计图得出参赛学生的总人数,根据中位数的定义计算即可得答案.
【详解】
∵参赛学生的总人数为30+60+90+90=270(人),
∴这次知识竞赛成绩的中位数为从低到高排列的第135、136位的平均数,
∴这次知识竞赛成绩的中位数在80分~90分之间,
故选:C.
【点睛】
本题考查中位数,熟练掌握中位数的定义及计算方法是解题关键.
5.D
【分析】
根据众数和中位数的概念可得出结论.
【详解】
一组数据中出现次数最多的数值是众数;将数据从小到大排列,当项数为奇数时中间的数为中位数,当项数为偶数时中间两个数的平均数为中位数;由题可知,小明所说的是多数人的分数,是众数,小英所说的为排在中间人的分数,是中位数.
故选为D.
【点睛】
本题考查众数和中位数的定义,熟记定义是解题的关键.
6.B
【详解】
分析:根据众数、平均数、频数、方差的概念分析.
详解:众数、平均数是反映一组数据的集中趋势,而频数是数据出现的次数,只有方差是反映数据的波动大小的.故为了判断成绩是否稳定,需要知道的是方差.
故选B.
点睛:此题考查统计学的相关知识.注意:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.A
【分析】
先找到四人中平均数大的,即成绩好的;再从平均成绩好的人中选择方差小,即成绩稳定的,从而得出答案.
【详解】
解:∵,
∴四位同学中甲、丙的平均成绩较好,
又∵S甲2<S丙2,
∴甲的成绩好又稳定,
故选:A.
【点睛】
本题考查平均数和方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
8.甲的波动比乙的波动大.
【分析】
根据方差的定义,方差越小数据越稳定,故可得到正确答案.
【详解】
解:根据方差的意义,甲样本的方差大于乙样本的方差,故甲的波动比乙的波动大.
故答案:甲的波动比乙的波动大.
【点睛】
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
9.
【分析】
由一组数据4,x,2,3,6的平均数是4,可列方程:再解方程可得答案.
【详解】
解: 一组数据4,x,2,3,6的平均数是4,
故答案为:
【点睛】
本题考查的是平均数的含义,掌握平均数的计算是解题的关键.
10.乙
【分析】
先由平均数的公式计算出乙队的平均成绩,再根据方差的公式求出乙队的方差,然后根据方差的意义即可得出答案.
【详解】
解:乙队的平均成绩为(10+9+5+8+8)=8(分),
其方差S2乙=[(10﹣8)2+(9﹣8)2+(5﹣8)2+(8﹣8)2+(8﹣8)2]=2.8.
∵22.8,即S2甲S2乙,
∴乙队成绩波动较大.
故答案为:乙.
【点睛】
本题主要考查平均数与方差,掌握平均数与方差的求法是解题的关键.
11.0.4
【分析】
先由平均数的公式计算出这组数据的平均数,再根据方差的公式进行计算即可.
【详解】
这组数据的平均数是(1+2+2+2+3)÷5=2
则这组数据的方差是:
故答案为:0.4.
【点睛】
本题考查了求方差,熟记公式是解题关键.
12.11
【分析】
根据加权平均数的计算方法是求出所有糖果的总钱数,然后除以糖果的总质量.
【详解】
解:售价应定为每千克(元.
故答案为:11.
【点睛】
本题考查的是加权平均数的求法,本题易出现的错误是对加权平均数的理解不正确,而求10、11、14这三个数的平均数.
13.乙班
【分析】
根据方差的意义(方差越小数据越稳定)进行判断.
【详解】
解:因为S甲 =235,S乙 =201,
则乙的方差小于甲的方差,
所以成绩较为整齐的是乙班.
故答案为:乙班.
【点睛】
本题考查了方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
14.众数
【详解】
本题考查的是众数的定义
根据众数的定义即可解答.
一组数据中出现次数最多的数据就是这组数据的众数.
15.8.7
【分析】
根据扇形统计图获取信息,利用加权平均数的定义列式计算即可.
【详解】
解:3种盒饭的价格平均数是6×25%+8×15%+10×60%=8.7(元),
故答案为:8.7.
【点睛】
本题考查获取扇形统计图信息,加权平均数,掌握获取扇形统计图信息,加权平均数,会利用加权平均数解决问题是关键.
16.15.5
【分析】
中位数是将一组数据按照大小顺序排列后,取最中间或最中间两个数的平均数,根据中位数的定义即可得出答案.
【详解】
解:将这30颗黄豆芽的长度排序后,第15,16个数据分别为15mm,16mm,
所以中位数为: (mm),
故答案为:15.5.
【点睛】
本题主要考查了中位数的定义,解决本题的关键是要熟练掌握中位数的定义.
17.(1)见解析(2)8万元,8万元,8.12万元(3)384人
【分析】
试题分析:(1)根据扇形中各部分所占的百分比的和是1,即可求得3万元的员工所占的百分比,然后根据百分比的意义求得直方图中缺少部分的人数;
(2)根据众数、中位数以及平均数的定义求解;
(3)利用总数1200乘以对应的比例即可求解.
【详解】
试题解析:(1)3万元的员工的百分比为:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取员工总数为:4÷8%=50(人)
5万元的员工人数为:50×24%=12(人)
8万元的员工人数为:50×36%=18(人)
(2)每人所创年利润的众数是 8万元,每人所创年利润的中位数是8万元,
平均数是:(3×4+5×12+8×18+10×10+15×6)=8.12万元.
故答案为8万元,8万元,8.12万元.
(3)1200×=384(人).
答:在公司1200员工中有384人可以评为优秀员工.
【点睛】
考点: 条形统计图;用样本估计总体;扇形统计图;加权平均数;中位数.
18.(1)3小时,3小时,3小时,补图见解析;(2)1360人
【分析】
(1)首先求得平均每天作业用时是4小时的人数,然后利用众数,中位数,平均数的定义即可求解;
(2)利用总人数2000乘以每天做作业时间在3小时内(含3小时)的同学所占的比例即可求解.
【详解】
(1)每天作业用时是4小时的人数是:50-6-12-16-8=8(人),
∵每天作业用时是3小时的人数最多,是16人,
∴众数是3小时;
∵从小到大排列后排在第25和第26位的都是每天作业用时是3小时的人,
∴中位数是3小时;
平均数是(小时),
补全条形统计图如图所示:
故答案为:3小时、3小时、3小时;
(3)2000×(人),
答:估计该校全体学生每天组作业时间在3小时内(含3小时)的同学共有1360人.
【点睛】
本题考查了平均数、中位数、众数的意义和计算方法,掌握平均数、中位数、众数的计算方法是正确计算的前提,样本估计总体是统计中常用的方法.
19.(1)补图见解析;(2)1.5,1.5;(3)被调查同学的平均阅读时间为1.32小时;(4)290人.
【分析】
(1)由条形图知,周末阅读1小时的有30人,由扇形图可知,周末阅读1小时的人数占总人数的30%,将30除以30%先解得总人数,再减去各项人数即可解题;
(2)众数是一组数据中出现最多次的数,中位数是将这组数据按顺序排列,位于正中间的一个数(或正中间的两个数的平均值),据此解题;
(3)将计算各时间段阅读的时间总和除以100即可;
(4)先周末阅读时间不低于1.5小时的人数占总人数的比例,再乘以500即可解题.
【详解】
解:(1)由题意可得,本次调查的学生数为:30÷30%=100(人),
阅读时间1.5小时的学生数为:100﹣12﹣30﹣18=40(人),
补全的条形统计图如图所示,
(2)由补全的条形统计图可知,有40人周末阅读时间在1.5小时,其他时间段的人数都比40少,即被调查的学生周末阅读时间众数是1.5小时;
总共调查100个数据,位于正中间的数是第50个与第51个数,即中位数是1.5小时,
故答案为:1.5,1.5;
(3)所有被调查学生阅读时间的平均数为:×(12×0.5+30×1+40×1.5+18×2)=1.32小时,即所有被调查同学的平均阅读时间为1.32小时;
(4)估计周末阅读时间不低于1.5小时的人数为500×=290(人).
【点睛】
本题考查条形统计图与扇形统计图,涉及众数、中位数、平均数、用样本估计总体等知识,是重要考点,难度较易,掌握相关知识是解题关键.
20.(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【分析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【详解】
解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
【点睛】
本题考查方差、中位数和众数:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
21.(1)7,7,7.5,3;(2)小王的成绩比较好;(3)小王的成绩比较好;(4)小王更有潜力
【分析】
(1)根据中位数,平均数的定义求解即可;
(2)从平均数和中位数相结合来分析可得结论;
(3)从平均数和命中9环以上的次数相结合来分析可得结论;
(4)从折线图上两人射击命中环数的走势分析可得结论.
【详解】
解:(1)小张的中位数为7,
小王的平均数,
小王的中位数,
小王命中9环及以上次数为3.
故答案为:7,7,7.5,3.
(2)从平均数看两人的成绩一样,
从中位数来看小王的成绩比较好.
综上所述,小王的成绩比较好.
(3)从平均数和命中9环以上的次数相结合来看,小王的成绩比较好.
(4)从折线图上两人射击命中环数的走势相结合来看,小王更有潜力.
【点睛】
本题考查折线统计图,中位数,平均数等知识,解题的关键是理解中位数,平均数的定义,属于中考常考题型.
22.班长应当选
【分析】
根据三项成绩的不同权重,分别计算三人的成绩.
【详解】
解:班长的成绩==26.2(分),
学习委员的成绩==25.8(分),
团支部书记的成绩==25.4(分),
∵26.2>25.8>25.4,
∴班长应当选.
【点睛】
本题考查了加权成绩的计算.解题的关键是掌握加权平均数的定义.
23.乙,理由见解析
【分析】
首先根据加权平均数的计算方法,分别求出甲、乙的平均成绩各是多少;然后比较大小,判断出谁会被公司录取即可.
【详解】
解:甲的平均成绩为:(分,
乙的平均成绩为:(分,
,
乙的平均成绩较高,
乙会被公司录取.
【点睛】
本题考查了加权平均数的知识,解题的关键是牢记公式并正确的运算.
24.(1)86分,86分;(2)八(1)班的成绩较为整齐
【分析】
(1)根据每个班5名学生的成绩,求出对应班级的平均成绩即可得到答案;
(2)根据(1)中求得的每个班级的平均成绩,求出对应的方差,然后判断即可得到答案.
【详解】
解:(1)由条形分布图可知:
八(1)班的5名学生的成绩分别为:80、80、90、80、100
八(2)班的5名学生的成绩分别为:80、100、95、70、85
∴八(1)班的5名学生的平均成绩(分)
八(2)班的5名学生的平均成绩(分)
答:两个班的平均成绩各是86分、86分;
(2)八(1)班的5名学生成绩的方差
八(2)班的5名学生成绩的方差
∴八(1)班的5名学生成绩的方差小于八(2)班的5名学生成绩的方差
∴八(1)班的成绩较为整齐.
【点睛】
本题主要考查了平均数和方差,并用方差比较稳定性,解题的关键在于能够熟练掌握相关知识进行求解.
25.(1)85,85,100;(2)八(A)班成绩好些.因为两个班的平均数一样,八(A)班的中位数高,所以八(A)班成绩好些.
【分析】
(1)观察统计图分别写出八(A)班和八(B)班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可;
(2)在平均数相同的情况下,中位数高的成绩较好.
【详解】
解:(1)由图可知八(A)班5名选手的复赛成绩为:75、80、85、85、100,
八(B)班5名选手的复赛成绩为:70、100、100、75、80,
八(A)的平均数为(75+80+85+85+100)÷5=85,
八(A)的中位数为85,
八(A)的众数为85,
把八(B)的成绩按从小到大的顺序排列为:70、75、80、100、100,
八(B)班的中位数是80;
八(B)班的众数是100;
八(B)的平均数为(70+75+80+100+100)÷5=85,
故答案是:85,85,100;
(2)八(A)班成绩好些.因为两个班的平均数一样,八(A)班的中位数高,所以八(A)班成绩好些.
【点睛】
本题考查了中位数、众数以及平均数的求法,并用这些统计量进行决策,解题的关键是牢记这些统计量的意义,并能熟练运用计算公式.
26.乙班将获胜
【分析】
根据加权平均数的计算公式带入求平均数即可;
【详解】
解:甲班平均成绩: (分),
乙班的平均成绩: (分),
∵ ,
∴乙班将获胜.
【点睛】
此题考查利用加权平均数做决策,考查加权平均数的计算,难度一般.
答案第1页,共2页
