2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册与导函数有关的图像问题课件(10张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册与导函数有关的图像问题课件(10张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 17:27:26 | ||
图片预览


文档简介
(共10张PPT)
与导函数有关的图像问题
导数判断函数的单调性的一般步骤:
(1)确定函数y=f(x)的定义域;
(2)求出导数f′(x)的零点;
(3)解不等式f′(x)>0,函数在解集与定义域的交集上单调递增.
(4)解不等式f′(x)<0,函数在解集与定义域的交集上单调递减.
回顾单调性:
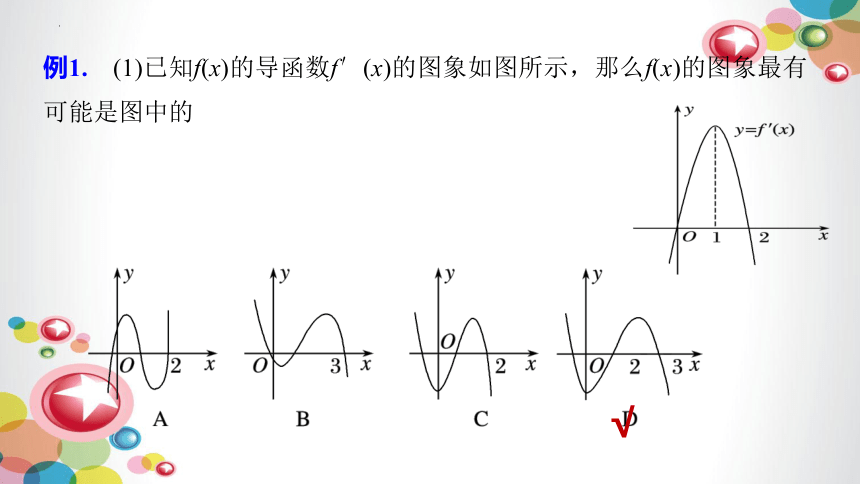
例1. (1)已知f(x)的导函数f′(x)的图象如图所示,那么f(x)的图象最有可能是图中的
√
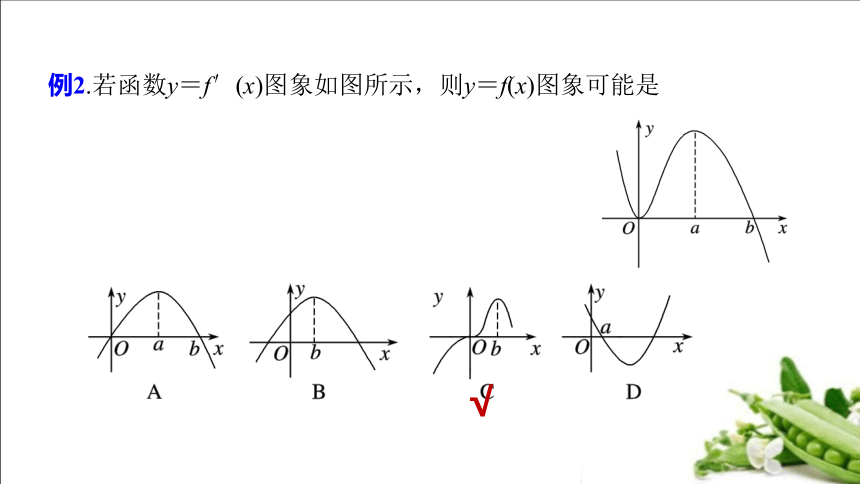
例2.若函数y=f′(x)图象如图所示,则y=f(x)图象可能是
√
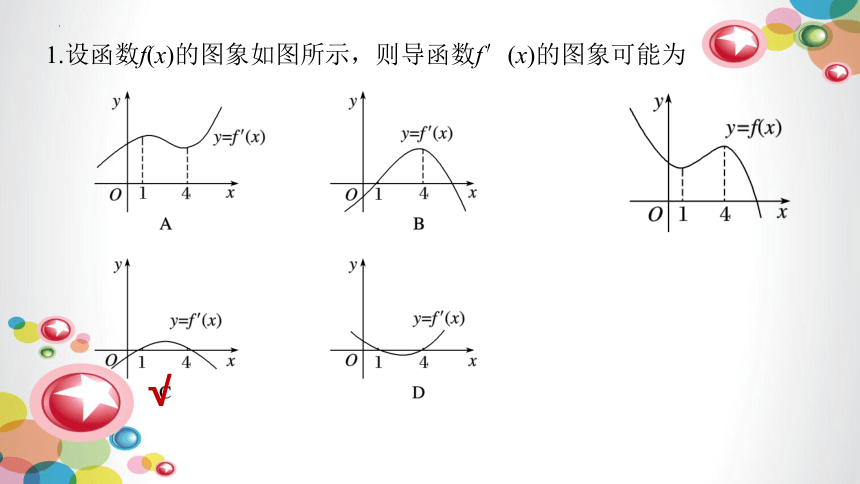
1.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为
√
例3. 观察下图,试分析函数增长或减少的速度与导数的大小关系?
知识归纳:
函数图象的变化趋势与导数的绝对值的大小的关系
一般地,设函数y=f(x),在区间(a,b)上:
导数的绝对值 函数值变化 函数的图象
越大 快 比较“陡峭”(向上或向下)
越小 慢 比较“平缓”(向上或向下)
注意点:分析图象的变化与导数的绝对值的大小关系.
例3 如图所示为函数y=f(x),y=g(x)的导函数的图象,那么y=f(x),y=g(x)的图象可能是
√
跟踪训练3 若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是
√
1.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象的大致形状是
√
分析: 由已知图象可知,f(x)先减后增再单调性不变,则f′(x)先小于零后大于零最后等于0.
与导函数有关的图像问题
导数判断函数的单调性的一般步骤:
(1)确定函数y=f(x)的定义域;
(2)求出导数f′(x)的零点;
(3)解不等式f′(x)>0,函数在解集与定义域的交集上单调递增.
(4)解不等式f′(x)<0,函数在解集与定义域的交集上单调递减.
回顾单调性:
例1. (1)已知f(x)的导函数f′(x)的图象如图所示,那么f(x)的图象最有可能是图中的
√
例2.若函数y=f′(x)图象如图所示,则y=f(x)图象可能是
√
1.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为
√
例3. 观察下图,试分析函数增长或减少的速度与导数的大小关系?
知识归纳:
函数图象的变化趋势与导数的绝对值的大小的关系
一般地,设函数y=f(x),在区间(a,b)上:
导数的绝对值 函数值变化 函数的图象
越大 快 比较“陡峭”(向上或向下)
越小 慢 比较“平缓”(向上或向下)
注意点:分析图象的变化与导数的绝对值的大小关系.
例3 如图所示为函数y=f(x),y=g(x)的导函数的图象,那么y=f(x),y=g(x)的图象可能是
√
跟踪训练3 若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是
√
1.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象的大致形状是
√
分析: 由已知图象可知,f(x)先减后增再单调性不变,则f′(x)先小于零后大于零最后等于0.
