第六章 计数原理6.2 排列与组合6.2.1排列14张ppt
文档属性
| 名称 | 第六章 计数原理6.2 排列与组合6.2.1排列14张ppt |  | |
| 格式 | zip | ||
| 文件大小 | 278.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 20:17:51 | ||
图片预览





文档简介
(共14张PPT)
第六章
计数原理
6.2排列与组合
6.2.1排列(第1课时)
1.分类加法计数原理:
完成一件事,有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法 …在第n类方案中有mn种不同的方法.那么完成这件事共有 种不同的方法.
2.分步乘法计数原理:
完成一件事,需要分成n个步骤,做 第 1 步有m1种不同的方法,做第2步有m2种不同的方法…,做 第 n 步 有mn种不同的方法.那 么 完 成这件 事 共有 种不同的方法.
一、回顾旧知
N=m1+m2+…+mn
N=m1×m2×…×mn
分步乘法
分类加法
共同点
区别一
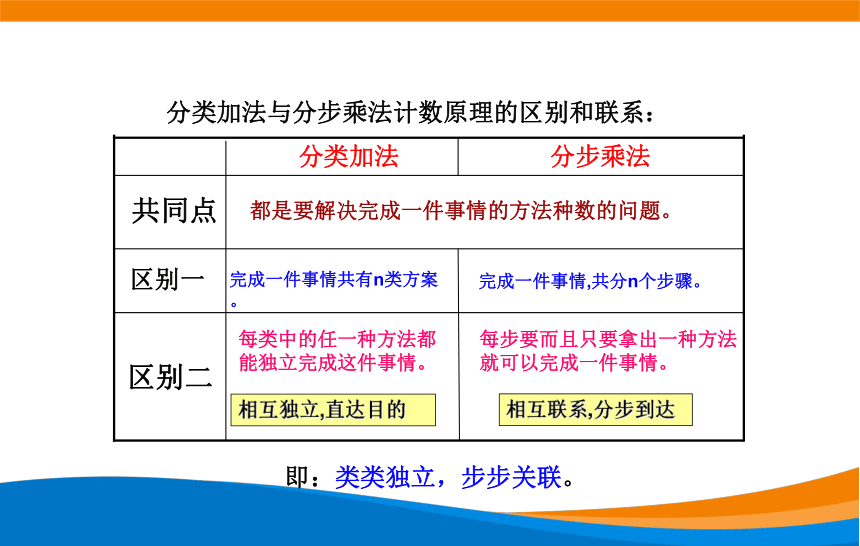
完成一件事情共有n类方案。
完成一件事情,共分n个步骤。
区别二
每类中的任一种方法都
能独立完成这件事情。
每步要而且只要拿出一种方法
就可以完成一件事情。
都是要解决完成一件事情的方法种数的问题。
分类加法与分步乘法计数原理的区别和联系:
相互独立,直达目的
相互联系,分步到达
即:类类独立,步步关联。
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
二、探究新知:
上午 下午 相应的排法
甲
乙
丙
乙
丙
甲乙
甲丙
分析:要完成的一件事情是“选出2名同学参加活动,1名参上午的活动,另1名参加下午的活动”,可以分步完成.
图6.2-1
解:从3名同学中选出2名同学参加活动,1名上午,另1名下午,可以分两个步骤完成:
乙甲
乙丙
丙甲
丙乙
甲
乙
甲
丙
第1步,确定参加上午活动的同学,从3人中任选1人,有3种选法;
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人去选,有2种选法.
根据分步乘法计数原理,不同选法的种数N=3×2=6.
6种选法如图6.2-1所示
探究1:若把上面问题中被取的对象叫做元素,于是问题1就可以叙述为:
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
不同的排列:ab, ac, ba, bc, ca, cb
不同的排列方法种数: N=3×2=6.
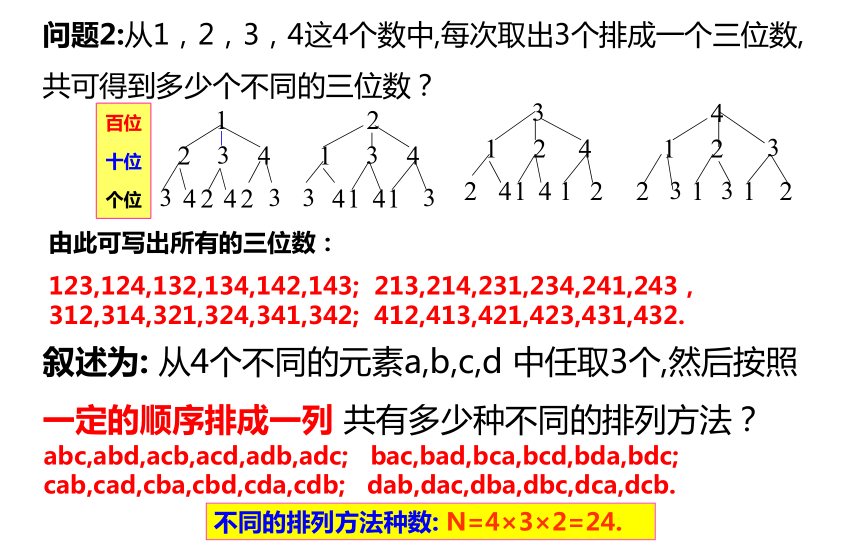
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
叙述为: 从4个不同的元素a,b,c,d 中任取3个,然后按照一定的顺序排成一列 共有多少种不同的排列方法?
abc,abd,acb,acd,adb,adc; bac,bad,bca,bcd,bda,bdc;
cab,cad,cba,cbd,cda,cdb; dab,dac,dba,dbc,dca,dcb.
由此可写出所有的三位数:
123,124,132,134,142,143; 213,214,231,234,241,243,312,314,321,324,341,342; 412,413,421,423,431,432.
百位
十位
个位
不同的排列方法种数: N=4×3×2=24.
问题1
从甲、乙、丙3名同学中选出2名参加某天 的 一项活动,其中1名参加上午的活动,1名参加下午的活动,有哪些不同的排法
实质是:从3个不同的元素中,任取2个,按一定的顺序排成一列,有哪些不同的排法.
问题2
从1,2,3,4这4个数中,每次取出3个排成一个三位数,共 可 得到多少个不同的三位数?
实质是:从4个不同的元素中, 任取3个,按照一定的顺序排成一列,写出所有不同的排法.
排列
排列:
从n个不同元素中取出m (m ≤ n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
注意:
1).元素不能重复。
2).“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3).两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4).m<n时的排列叫选排列,m=n时的排列叫全排列。
5).为了使写出的所有排列情况既不重复也不遗漏, 最好采用“树形图”。
(有序性)
(互异性)
1 .判断下列“事情”是否为排列:
(1) 5人站成一排照相;
(2) 从全班50名同学中挑选4人;
(3) 从某6人中选取4人参加4×100m接力赛;
(4) 将3本不同的书分发给3个人.
是
是
是
否
三、巩固新知
2.判断下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3三个数字中,任选两个做除法,其不同结果有多少种?
(3)从1到10十个自然数中任取两个组成点的坐标,可得多少个不同的点的坐标?
(4)10个学生排队照相,则不同的站法有多少种?
(从中归纳这几类问题的区别)
不是排列
是排列
是排列
是排列
三、巩固新知:
例1.某省中学生足球赛每组有6支队,每支队都要与同组的其他各队在主、客场 分别 比赛1场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的1场比赛, 可以看作是从该组6支队中选2支,按“主队、客队”的顺序排成一个排列.
解:可以先从6支队选1支队为主队,然后从剩下的5支队中选1支队为客队,按分步乘法计数原理,每组进行的比赛场数为:6×5=30.
三、巩固新知:
例2.(1).一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
(2).学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?.
分析:3名同学每人从5盘不同菜中取1盘菜,可看作从5盘菜中任取3盘放在3个位置(给3名同学)的一个排列; 而3名同学每人从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列.
解:(1).可以先从这5盘菜中取1盘给同学甲,然后从剩下4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为:5×4×3=60.
(2).可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从从5种菜中选1种,有5种选法; 最后让同学丙从5种菜中选1种,有5种选法. 按分步乘法计数原理,不同的取法种数为:5×5×5=125.
三、巩固新知:
四. 巩固练习:
课本16页练习
五.课堂小结
排列:从n个不同元素中选出m(m≤n)个元素,并按一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
关键点:a.互异性(被选、所选元素互不相同)
b.有序性(所选元素有先后位置等顺序之分)
第六章
计数原理
6.2排列与组合
6.2.1排列(第1课时)
1.分类加法计数原理:
完成一件事,有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法 …在第n类方案中有mn种不同的方法.那么完成这件事共有 种不同的方法.
2.分步乘法计数原理:
完成一件事,需要分成n个步骤,做 第 1 步有m1种不同的方法,做第2步有m2种不同的方法…,做 第 n 步 有mn种不同的方法.那 么 完 成这件 事 共有 种不同的方法.
一、回顾旧知
N=m1+m2+…+mn
N=m1×m2×…×mn
分步乘法
分类加法
共同点
区别一
完成一件事情共有n类方案。
完成一件事情,共分n个步骤。
区别二
每类中的任一种方法都
能独立完成这件事情。
每步要而且只要拿出一种方法
就可以完成一件事情。
都是要解决完成一件事情的方法种数的问题。
分类加法与分步乘法计数原理的区别和联系:
相互独立,直达目的
相互联系,分步到达
即:类类独立,步步关联。
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
二、探究新知:
上午 下午 相应的排法
甲
乙
丙
乙
丙
甲乙
甲丙
分析:要完成的一件事情是“选出2名同学参加活动,1名参上午的活动,另1名参加下午的活动”,可以分步完成.
图6.2-1
解:从3名同学中选出2名同学参加活动,1名上午,另1名下午,可以分两个步骤完成:
乙甲
乙丙
丙甲
丙乙
甲
乙
甲
丙
第1步,确定参加上午活动的同学,从3人中任选1人,有3种选法;
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人去选,有2种选法.
根据分步乘法计数原理,不同选法的种数N=3×2=6.
6种选法如图6.2-1所示
探究1:若把上面问题中被取的对象叫做元素,于是问题1就可以叙述为:
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
不同的排列:ab, ac, ba, bc, ca, cb
不同的排列方法种数: N=3×2=6.
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
叙述为: 从4个不同的元素a,b,c,d 中任取3个,然后按照一定的顺序排成一列 共有多少种不同的排列方法?
abc,abd,acb,acd,adb,adc; bac,bad,bca,bcd,bda,bdc;
cab,cad,cba,cbd,cda,cdb; dab,dac,dba,dbc,dca,dcb.
由此可写出所有的三位数:
123,124,132,134,142,143; 213,214,231,234,241,243,312,314,321,324,341,342; 412,413,421,423,431,432.
百位
十位
个位
不同的排列方法种数: N=4×3×2=24.
问题1
从甲、乙、丙3名同学中选出2名参加某天 的 一项活动,其中1名参加上午的活动,1名参加下午的活动,有哪些不同的排法
实质是:从3个不同的元素中,任取2个,按一定的顺序排成一列,有哪些不同的排法.
问题2
从1,2,3,4这4个数中,每次取出3个排成一个三位数,共 可 得到多少个不同的三位数?
实质是:从4个不同的元素中, 任取3个,按照一定的顺序排成一列,写出所有不同的排法.
排列
排列:
从n个不同元素中取出m (m ≤ n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
注意:
1).元素不能重复。
2).“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3).两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4).m<n时的排列叫选排列,m=n时的排列叫全排列。
5).为了使写出的所有排列情况既不重复也不遗漏, 最好采用“树形图”。
(有序性)
(互异性)
1 .判断下列“事情”是否为排列:
(1) 5人站成一排照相;
(2) 从全班50名同学中挑选4人;
(3) 从某6人中选取4人参加4×100m接力赛;
(4) 将3本不同的书分发给3个人.
是
是
是
否
三、巩固新知
2.判断下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3三个数字中,任选两个做除法,其不同结果有多少种?
(3)从1到10十个自然数中任取两个组成点的坐标,可得多少个不同的点的坐标?
(4)10个学生排队照相,则不同的站法有多少种?
(从中归纳这几类问题的区别)
不是排列
是排列
是排列
是排列
三、巩固新知:
例1.某省中学生足球赛每组有6支队,每支队都要与同组的其他各队在主、客场 分别 比赛1场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的1场比赛, 可以看作是从该组6支队中选2支,按“主队、客队”的顺序排成一个排列.
解:可以先从6支队选1支队为主队,然后从剩下的5支队中选1支队为客队,按分步乘法计数原理,每组进行的比赛场数为:6×5=30.
三、巩固新知:
例2.(1).一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
(2).学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?.
分析:3名同学每人从5盘不同菜中取1盘菜,可看作从5盘菜中任取3盘放在3个位置(给3名同学)的一个排列; 而3名同学每人从食堂窗口的5种菜中选1种,每人都有5种选法,不能看成一个排列.
解:(1).可以先从这5盘菜中取1盘给同学甲,然后从剩下4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为:5×4×3=60.
(2).可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从从5种菜中选1种,有5种选法; 最后让同学丙从5种菜中选1种,有5种选法. 按分步乘法计数原理,不同的取法种数为:5×5×5=125.
三、巩固新知:
四. 巩固练习:
课本16页练习
五.课堂小结
排列:从n个不同元素中选出m(m≤n)个元素,并按一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
关键点:a.互异性(被选、所选元素互不相同)
b.有序性(所选元素有先后位置等顺序之分)
