小学数学 苏教版 六年级下册 二 圆柱和圆锥圆柱和圆锥整理与练习课件(41张ppt)
文档属性
| 名称 | 小学数学 苏教版 六年级下册 二 圆柱和圆锥圆柱和圆锥整理与练习课件(41张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 13:30:35 | ||
图片预览


文档简介
(共41张PPT)
圆柱和圆锥整理与练习(1)
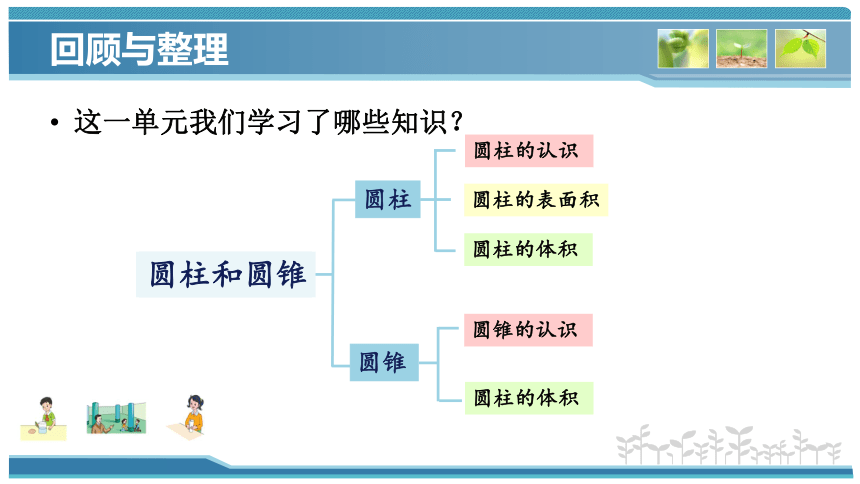
这一单元我们学习了哪些知识?
回顾与整理
圆柱和圆锥
圆柱
圆柱的认识
圆锥的认识
圆柱的表面积
圆锥
圆柱的体积
圆柱的体积
圆柱和圆锥
1.圆柱和圆锥各有哪些特征?
底面
底面
侧面
高
高
回顾与整理
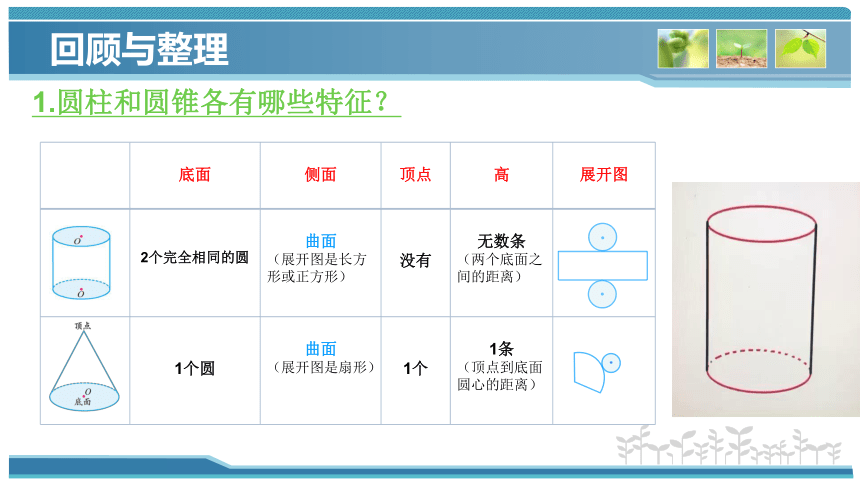
1.圆柱和圆锥各有哪些特征?
底面 侧面 顶点 高
展开图
2个完全相同的圆 曲面 (展开图是长方形或正方形) 没有 无数条 (两个底面之间的距离)
1个圆 曲面 (展开图是扇形) 1个 1条 (顶点到底面圆心的距离)
回顾与整理
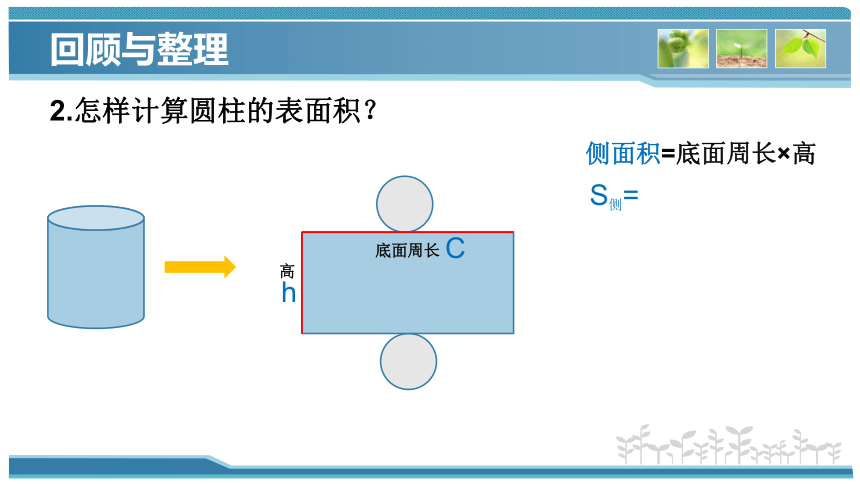
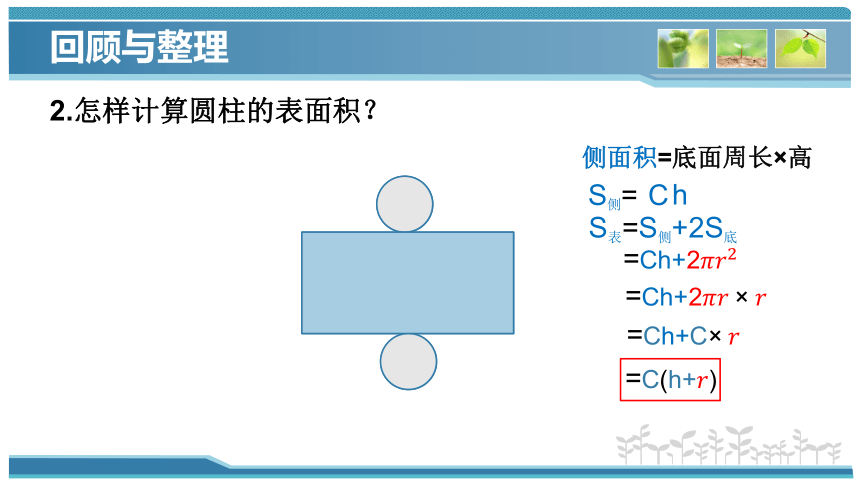
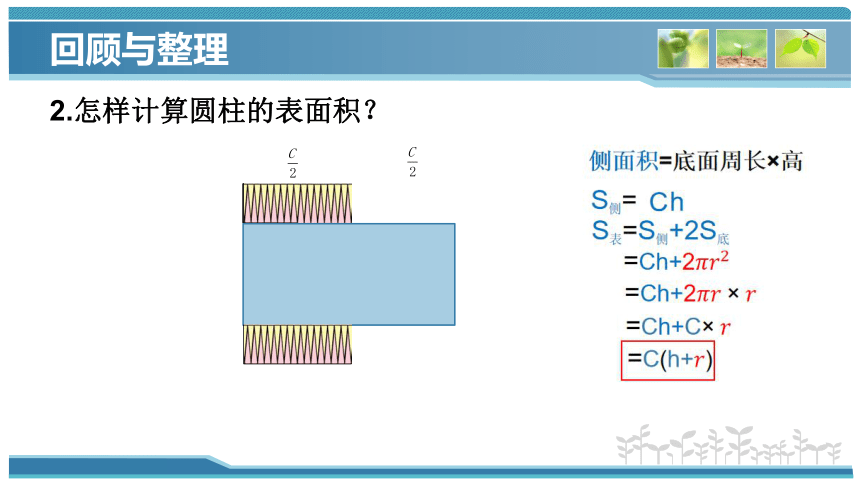
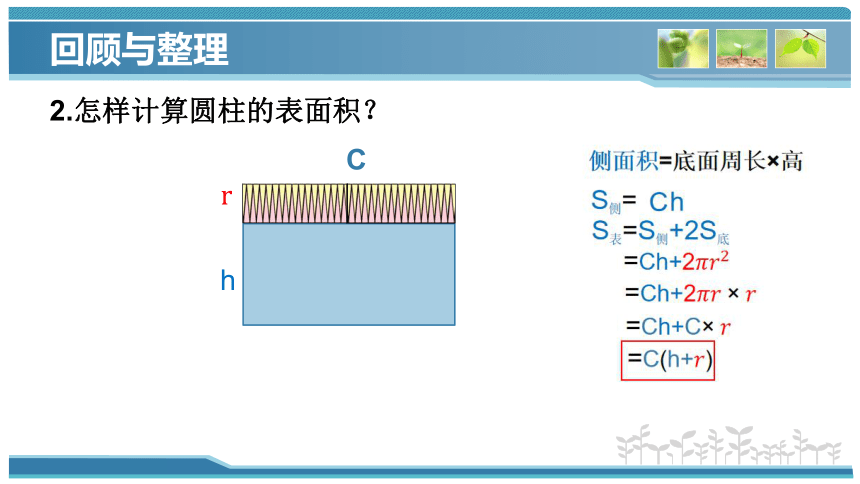
2.怎样计算圆柱的表面积?
回顾与整理
底面周长
高
侧面积=底面周长×高
S侧=
C
h
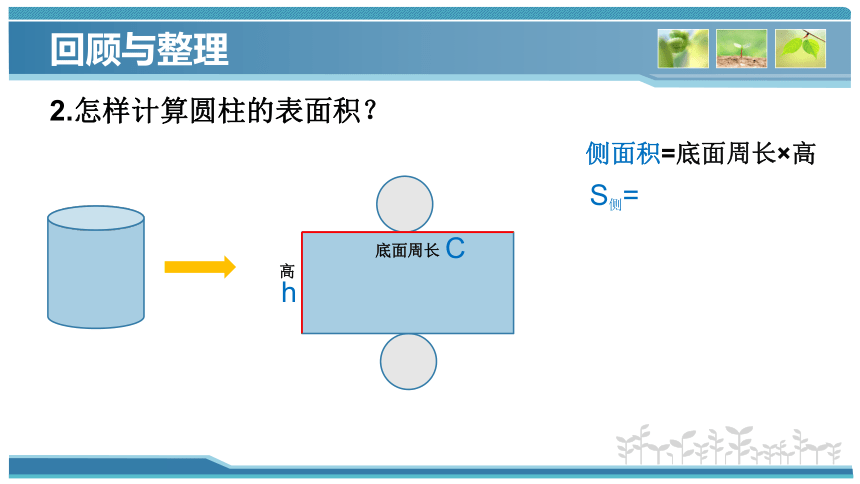
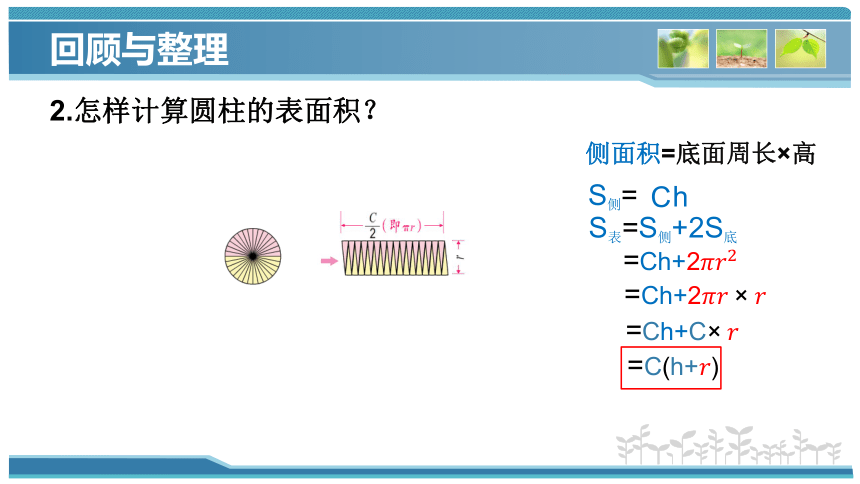
2.怎样计算圆柱的表面积?
回顾与整理
底面周长
高
S侧=
C
h
侧面积=底面周长×高
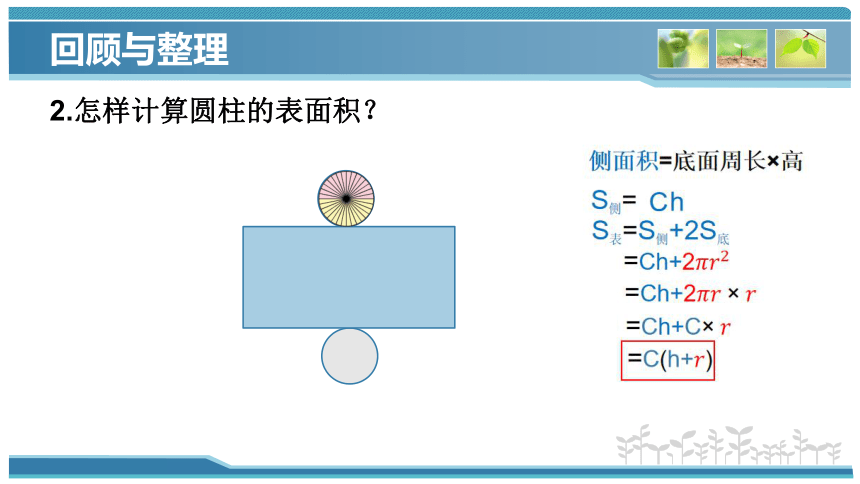
2.怎样计算圆柱的表面积?
侧面积=底面周长×高
S侧=
C
h
S表=S侧+2S底
=Ch+2
=Ch+2
=C(h+)
=Ch+C
回顾与整理
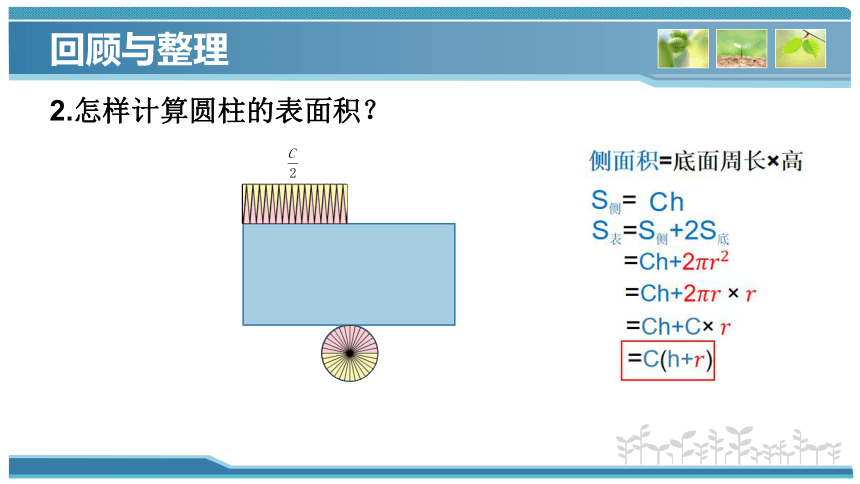
2.怎样计算圆柱的表面积?
回顾与整理
S侧=
C
h
S表=S侧+2S底
=Ch+2
=Ch+2
=C(h+)
=Ch+C
侧面积=底面周长×高
2.怎样计算圆柱的表面积?
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
h
C
r
练习与应用
做一个底面周长12.56分米,高8分米的圆柱形铁皮油桶,至少用铁皮多少平方分米?
做一个底面周长12.56分米,高8分米的圆柱形铁皮油桶,至少用铁皮多少平方分米?
方法一:
S表=C(h+r)
12.56×(8+12.56÷3.14÷2)
= 12.56 × 10
= 125.6(平方分米)
练习与应用
做一个底面周长12.56分米,高8分米的圆柱形铁皮油桶,至少用铁皮多少平方分米?
方法一: 方法二:
S表=C(h+r)
12.56×(8+12.56÷3.14÷2)
= 12.56 × 10
=125.6(平方分米)
S表=S侧+2S底
答:至少用铁皮125.6平方分米。
练习与应用
12.56×8+2×
= 12.56×8+8
= 125.6(平方分米)
思路点拨:
①轮宽是指谁的长度?
②求“前轮滚动一周所压路的面积”,就是求谁的面积?
圆柱形前轮的侧面积
2. 一种压路机的前轮是圆柱形的,轮宽
1.6米,直径是0.8米。前轮滚动一周,
压路的面积是多少平方米
练习与应用
圆柱形车轮的高
1.6米
2. 一种压路机的前轮是圆柱形的,轮宽
1.6米,直径是0.8米。前轮滚动一周,
压路的面积是多少平方米
S侧=
0.8 ×1.6
= 1.28 (平方米)
答:压路的面积是1.28平方米。
练习与应用
思路点拨:
①铁箍的长度是指谁的长度?
②求“做无盖水桶至少要用木板多少平方分米”,是要求
圆柱哪几个面的面积?
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约
长15.7分米。
(1)做这个水桶至少要用木板多少平方分米?
练习与应用
圆柱底面周长
圆柱侧面积与一个底面积的和
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约
长15.7分米。
(1)做这个水桶至少要用木板多少平方分米?
S侧=ch
15.7×6
=94.2(平方分米)
S底= r
3.14×(15.7÷3.14÷2)
=19.625(平方分米)
94.2+19.625 =113.825(平方分米)
答:做这个水桶至少要用木板113.825平方分米。
练习与应用
解决圆柱表面积的实际问题要注意什么?
回顾与整理
1.要注意数据的合理选择,运用公式时直径、半径相互转化;
2.在解决实际问题时要注意认真审题,看清要计算圆柱哪几
个面的面积。
3.我们是怎样发现圆柱体积公式的?
回顾与整理
长方体的体积与圆柱的体积相等。
长方体的高等于
圆柱的高。
长方体的底面积等于圆柱的底面积。
拼成的长方体与原来的圆柱有什么关系呢?
圆柱的体积 = 底面积×高
V圆柱 = Sh
回顾与整理
3.我们是怎样发现圆柱的体积公式的?
3.我们是怎样发现圆锥体积公式的?
回顾与整理
圆锥的体积是与它等底等高圆柱体积的 。
圆锥的体积 =底面积 × 高 ×
V圆锥 = S h
回顾与整理
名称 底面半径 底面直径 高 表面积 体积
圆柱 2cm 5cm
10cm 8cm
圆锥 5cm 1.2cm ——
0.6cm 1.8cm ——
小贴士:①选择合理的方式进行计算;
②为了计算方便,结果可以用含有“”的式子表示。
第一关:算一算,填一填。
练习与应用
名称 底面半径 底面直径 高 表面积 体积
圆柱 2cm 5cm
10cm 8cm
圆锥 5cm 1.2cm ——
0.6cm 1.8cm ——
4cm
5cm
2.5cm
1.2cm
20c
200c
2.5 c
0.216 c
28cm
130cm
小贴士:①选择合理的方式进行计算;
②为了计算方便,结果可以用含有“”的式子表示。
第一关:算一算,填一填。
练习与应用
练习与应用
第二关:生活应用小达人
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约 长15.7分米。
(2)这个水桶能盛120升水吗?
思路点拨:
要判断这个水桶能不能盛120升水,就是要比什么?
练习与应用
第二关:生活应用小达人
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约 长15.7分米。
(2)这个水桶能盛120升水吗?
方法一:
19.625×6=117.75(立方分米)
117.75立方分米=117.75升
117.75<120
方法二:
19.625×6<20×6
19.625<20
答:这个水桶不能盛120升水。
练习与应用
第二关:生活应用小达人
4.有一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?
(得数保留整数)
思路点拨:
要求这堆稻谷的重量应该先算什么?
练习与应用
第二关:生活应用小达人
4.有一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?
(得数保留整数)
V圆锥 = S h
×3.14 × 1.5
6.28 ×0.55≈3(吨)
答:这堆稻谷大约重3吨。
=6.28
(立方米)
练习与应用
第三关:解决问题小能手
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米。
(1)把它捏成底面积是15平方厘米的圆锥形,高是多少厘米?
思路点拨:
①把圆柱捏成圆锥什么变了,什么没变?
②等体积、等底面积的圆柱和圆锥的高有什么联系?
圆柱和圆锥的体积不变,在等体积等底面积的情况下,圆锥的高是圆柱的3倍。
练习与应用
第三关:解决问题小能手
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米。
(1)把它捏成底面积是15平方厘米的圆锥形,高是多少厘米?
方法一:
15×6×3÷15=18(厘米)
方法二:
6×3=18(厘米)
答:高是18厘米。
练习与应用
第三关:解决问题小能手
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米
(2)把它捏成高是6厘米的圆锥形,底面积是多少平方厘米?
通过刚才问题的解答,你又想到了怎样的解题方法呢?
15×3=45(平方厘米)
答:底面积是45平方厘米。
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
思路点拨:
①可以分别算出圆柱和圆锥的体积,再相加求出它们体积之和;
②利用等底等高的圆柱与圆锥体积的关系,用倍差关系来解决。
你能用不同的方法计算吗?
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法一:
(6÷2)2 ×12 + (6÷2)2 ×12
=108 +36
=144 (立方厘米)
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法二:
×(6÷2)2 ×12 ×(1 + )
=108 ×
=144 (立方厘米)
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法二:
×(6÷2)2 ×12 ×(1 + )
=108 ×
=144 (立方厘米)
方法三:
×(6÷2)2×12 ×(1 + 3 )
=36 × 4
=144 (立方厘米)
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法四:
(6÷2)2 ×(12 +12÷3)
=9× 16
=144 (立方厘米)
收获与反思
通过这节课的学习,你有哪些收获和体会?
课后练习
“圆柱和圆锥的整理与练习(1)”课后检测
一、火眼金睛
1.从圆锥的顶点到底面上的任何一点的距离就是圆锥的高。 ( )
2.圆柱的底面半径扩大到原来的2倍,高不变,则侧面积扩大到原来的4倍。( )
3.把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。 ( )
4.如果两个圆柱的侧面积相等,那么它们的体积也相等。 ( )
5.将一个圆柱切拼成一个近似的长方体,这个长方体和原来的圆柱相比,
体积不变,表面积变小。 ( )
课后练习
圆柱和圆锥整理与练习(1)
这一单元我们学习了哪些知识?
回顾与整理
圆柱和圆锥
圆柱
圆柱的认识
圆锥的认识
圆柱的表面积
圆锥
圆柱的体积
圆柱的体积
圆柱和圆锥
1.圆柱和圆锥各有哪些特征?
底面
底面
侧面
高
高
回顾与整理
1.圆柱和圆锥各有哪些特征?
底面 侧面 顶点 高
展开图
2个完全相同的圆 曲面 (展开图是长方形或正方形) 没有 无数条 (两个底面之间的距离)
1个圆 曲面 (展开图是扇形) 1个 1条 (顶点到底面圆心的距离)
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
底面周长
高
侧面积=底面周长×高
S侧=
C
h
2.怎样计算圆柱的表面积?
回顾与整理
底面周长
高
S侧=
C
h
侧面积=底面周长×高
2.怎样计算圆柱的表面积?
侧面积=底面周长×高
S侧=
C
h
S表=S侧+2S底
=Ch+2
=Ch+2
=C(h+)
=Ch+C
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
S侧=
C
h
S表=S侧+2S底
=Ch+2
=Ch+2
=C(h+)
=Ch+C
侧面积=底面周长×高
2.怎样计算圆柱的表面积?
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
2.怎样计算圆柱的表面积?
回顾与整理
h
C
r
练习与应用
做一个底面周长12.56分米,高8分米的圆柱形铁皮油桶,至少用铁皮多少平方分米?
做一个底面周长12.56分米,高8分米的圆柱形铁皮油桶,至少用铁皮多少平方分米?
方法一:
S表=C(h+r)
12.56×(8+12.56÷3.14÷2)
= 12.56 × 10
= 125.6(平方分米)
练习与应用
做一个底面周长12.56分米,高8分米的圆柱形铁皮油桶,至少用铁皮多少平方分米?
方法一: 方法二:
S表=C(h+r)
12.56×(8+12.56÷3.14÷2)
= 12.56 × 10
=125.6(平方分米)
S表=S侧+2S底
答:至少用铁皮125.6平方分米。
练习与应用
12.56×8+2×
= 12.56×8+8
= 125.6(平方分米)
思路点拨:
①轮宽是指谁的长度?
②求“前轮滚动一周所压路的面积”,就是求谁的面积?
圆柱形前轮的侧面积
2. 一种压路机的前轮是圆柱形的,轮宽
1.6米,直径是0.8米。前轮滚动一周,
压路的面积是多少平方米
练习与应用
圆柱形车轮的高
1.6米
2. 一种压路机的前轮是圆柱形的,轮宽
1.6米,直径是0.8米。前轮滚动一周,
压路的面积是多少平方米
S侧=
0.8 ×1.6
= 1.28 (平方米)
答:压路的面积是1.28平方米。
练习与应用
思路点拨:
①铁箍的长度是指谁的长度?
②求“做无盖水桶至少要用木板多少平方分米”,是要求
圆柱哪几个面的面积?
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约
长15.7分米。
(1)做这个水桶至少要用木板多少平方分米?
练习与应用
圆柱底面周长
圆柱侧面积与一个底面积的和
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约
长15.7分米。
(1)做这个水桶至少要用木板多少平方分米?
S侧=ch
15.7×6
=94.2(平方分米)
S底= r
3.14×(15.7÷3.14÷2)
=19.625(平方分米)
94.2+19.625 =113.825(平方分米)
答:做这个水桶至少要用木板113.825平方分米。
练习与应用
解决圆柱表面积的实际问题要注意什么?
回顾与整理
1.要注意数据的合理选择,运用公式时直径、半径相互转化;
2.在解决实际问题时要注意认真审题,看清要计算圆柱哪几
个面的面积。
3.我们是怎样发现圆柱体积公式的?
回顾与整理
长方体的体积与圆柱的体积相等。
长方体的高等于
圆柱的高。
长方体的底面积等于圆柱的底面积。
拼成的长方体与原来的圆柱有什么关系呢?
圆柱的体积 = 底面积×高
V圆柱 = Sh
回顾与整理
3.我们是怎样发现圆柱的体积公式的?
3.我们是怎样发现圆锥体积公式的?
回顾与整理
圆锥的体积是与它等底等高圆柱体积的 。
圆锥的体积 =底面积 × 高 ×
V圆锥 = S h
回顾与整理
名称 底面半径 底面直径 高 表面积 体积
圆柱 2cm 5cm
10cm 8cm
圆锥 5cm 1.2cm ——
0.6cm 1.8cm ——
小贴士:①选择合理的方式进行计算;
②为了计算方便,结果可以用含有“”的式子表示。
第一关:算一算,填一填。
练习与应用
名称 底面半径 底面直径 高 表面积 体积
圆柱 2cm 5cm
10cm 8cm
圆锥 5cm 1.2cm ——
0.6cm 1.8cm ——
4cm
5cm
2.5cm
1.2cm
20c
200c
2.5 c
0.216 c
28cm
130cm
小贴士:①选择合理的方式进行计算;
②为了计算方便,结果可以用含有“”的式子表示。
第一关:算一算,填一填。
练习与应用
练习与应用
第二关:生活应用小达人
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约 长15.7分米。
(2)这个水桶能盛120升水吗?
思路点拨:
要判断这个水桶能不能盛120升水,就是要比什么?
练习与应用
第二关:生活应用小达人
3.一个圆柱形水桶,高6分米。水桶外围的一圈铁箍大约 长15.7分米。
(2)这个水桶能盛120升水吗?
方法一:
19.625×6=117.75(立方分米)
117.75立方分米=117.75升
117.75<120
方法二:
19.625×6<20×6
19.625<20
答:这个水桶不能盛120升水。
练习与应用
第二关:生活应用小达人
4.有一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?
(得数保留整数)
思路点拨:
要求这堆稻谷的重量应该先算什么?
练习与应用
第二关:生活应用小达人
4.有一个近似于圆锥形的稻谷堆,底面直径是4米,高是1.5米。如果每立方米稻谷大约重0.55吨,这堆稻谷大约重多少吨?
(得数保留整数)
V圆锥 = S h
×3.14 × 1.5
6.28 ×0.55≈3(吨)
答:这堆稻谷大约重3吨。
=6.28
(立方米)
练习与应用
第三关:解决问题小能手
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米。
(1)把它捏成底面积是15平方厘米的圆锥形,高是多少厘米?
思路点拨:
①把圆柱捏成圆锥什么变了,什么没变?
②等体积、等底面积的圆柱和圆锥的高有什么联系?
圆柱和圆锥的体积不变,在等体积等底面积的情况下,圆锥的高是圆柱的3倍。
练习与应用
第三关:解决问题小能手
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米。
(1)把它捏成底面积是15平方厘米的圆锥形,高是多少厘米?
方法一:
15×6×3÷15=18(厘米)
方法二:
6×3=18(厘米)
答:高是18厘米。
练习与应用
第三关:解决问题小能手
5.一块圆柱形橡皮泥,底面积是15平方厘米,高是6厘米
(2)把它捏成高是6厘米的圆锥形,底面积是多少平方厘米?
通过刚才问题的解答,你又想到了怎样的解题方法呢?
15×3=45(平方厘米)
答:底面积是45平方厘米。
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
思路点拨:
①可以分别算出圆柱和圆锥的体积,再相加求出它们体积之和;
②利用等底等高的圆柱与圆锥体积的关系,用倍差关系来解决。
你能用不同的方法计算吗?
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法一:
(6÷2)2 ×12 + (6÷2)2 ×12
=108 +36
=144 (立方厘米)
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法二:
×(6÷2)2 ×12 ×(1 + )
=108 ×
=144 (立方厘米)
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法二:
×(6÷2)2 ×12 ×(1 + )
=108 ×
=144 (立方厘米)
方法三:
×(6÷2)2×12 ×(1 + 3 )
=36 × 4
=144 (立方厘米)
练习与应用
第三关:解决问题小能手
6.一个圆柱和一个圆锥,底面直径都是6厘米,高都是12厘米。它们的体积一共是多少立方厘米?
你能用不同的方法计算吗?
方法四:
(6÷2)2 ×(12 +12÷3)
=9× 16
=144 (立方厘米)
收获与反思
通过这节课的学习,你有哪些收获和体会?
课后练习
“圆柱和圆锥的整理与练习(1)”课后检测
一、火眼金睛
1.从圆锥的顶点到底面上的任何一点的距离就是圆锥的高。 ( )
2.圆柱的底面半径扩大到原来的2倍,高不变,则侧面积扩大到原来的4倍。( )
3.把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。 ( )
4.如果两个圆柱的侧面积相等,那么它们的体积也相等。 ( )
5.将一个圆柱切拼成一个近似的长方体,这个长方体和原来的圆柱相比,
体积不变,表面积变小。 ( )
课后练习
