小学数学 苏教版 六年级下册 二 圆柱和圆锥圆柱和圆锥整理与练习课件(33张ppt)
文档属性
| 名称 | 小学数学 苏教版 六年级下册 二 圆柱和圆锥圆柱和圆锥整理与练习课件(33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 13:33:57 | ||
图片预览








文档简介
(共33张PPT)
圆柱和圆锥整理与练习(2)
课后练习
一、火眼金睛
1.从圆锥的顶点到底面上的任何一点的距离就是圆锥的高。( )
×
解析:从圆锥的顶点到底面圆心的距离是圆锥的高。
2.圆柱的底面半径扩大到原来的2倍,高不变,则侧面积扩大到原来的
4倍。 ( )
×
解析:圆柱的侧面积=底面周长×高,S侧=2πrh,当圆柱底面半径扩大到原来的2倍,高不变时,侧面积也扩大到原来的2倍。
课后练习
一、火眼金睛
3.把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。
( )
√
4.如果两个圆柱的侧面积相等,那么它们的体积也相等。 ( )
×
解析:两个圆柱的侧面积相等仅仅说明半径和高的乘积相等,但底面半径和高不一定相等,所以体积也不一定相等。
解析:把一个圆柱削成一个最大的圆锥,削成的圆锥的体积是圆柱体积的 ,
削掉部分是圆柱体积的 ,即削掉部分的体积是圆锥体积的2倍。
课后练习
5.将一个圆柱切拼成一个近似的长方体,这个长方体和原来的圆柱相比,体积不变,表面积变小。 ( )
×
解析:将一个圆柱切拼成一个近似的长方体后,体积不变,但表面积增加两个侧面,即增加了2rh。
一、火眼金睛
课后练习
1.如果一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高和它的底面直径的比是( )
A. 1:1 B. 1:π C. 2:π D. π:1
二、精准选择
解析:圆柱的侧面展开后是正方形,则圆柱的底面周长和高相等,即h=πd,则h:d=πd:d=π:1。
D
课后练习
2.一根圆柱形木料的底面直径是12厘米,高是20厘米,把它截成三段,每段都是圆柱,截成三段后表面积增加了( )平方厘米。
A.48π B. 72π C. 720π D. 144π
二、精准选择
解析:把圆柱截成三段,每段都是圆柱,表面积增加了4个底面的面积,即π×(12÷2)2×4=144π
D
课后练习
二、精准选择
A
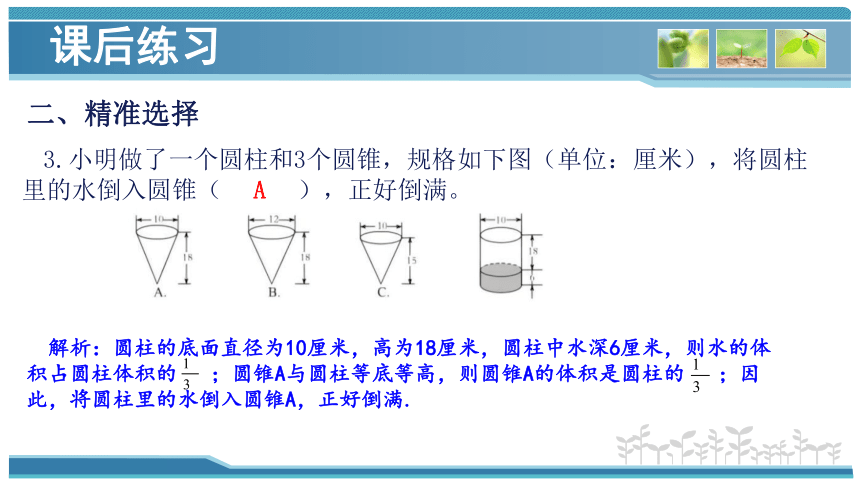
3.小明做了一个圆柱和3个圆锥,规格如下图(单位:厘米),将圆柱里的水倒入圆锥( ),正好倒满。
解析:圆柱的底面直径为10厘米,高为18厘米,圆柱中水深6厘米,则水的体积占圆柱体积的 ;圆锥A与圆柱等底等高,则圆锥A的体积是圆柱的 ;因此,将圆柱里的水倒入圆锥A,正好倒满.
课后练习
4.下面的几何体中,( )的体积不可以用“底面积×高”求得。
A. 长方体 B. 正方体 C. 圆柱 D. 圆锥
二、精准选择
D
解析:长方体、正方体、圆柱都是直柱体,它们的体积都可以用“底面积×高”计算,圆锥的体积是与它等底等高的圆柱体积的 ,V锥= ×底面积×高。
课后练习
二、精准选择
C
解析:甲沿底面切分,增加两个底面积,即增加2πy2 ;乙沿高切分,增加两个 长为高、宽为底面直径的长方形的面积,即增加4yh。
D
5.下面是两位同学对同一个圆柱的两种不同的切分(平均分成两块)方 法。甲切分后,表面积比原来增加( );乙切分后,表面积比原来增加( )。
A. πy B. 2yh C. 2πy2 D. 4yh
探索与发现1:
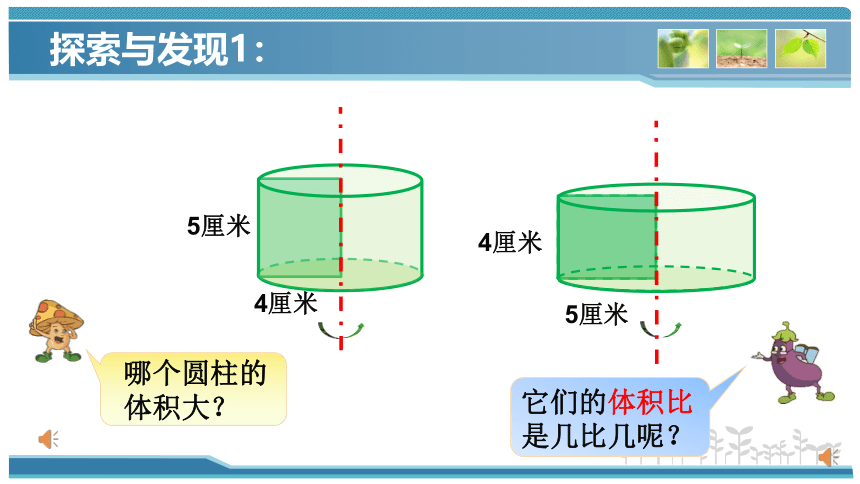
4厘米
5厘米
5厘米
4厘米
哪个圆柱的
体积大?
它们的体积比是几比几呢?
探索与发现1:
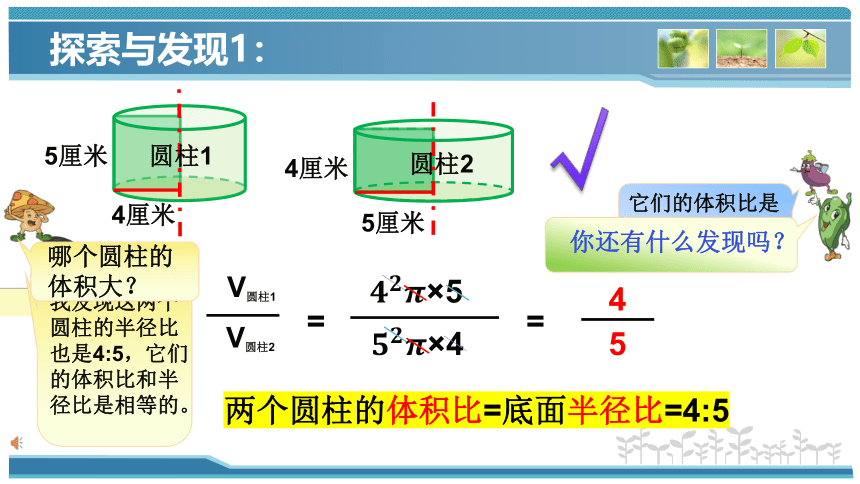
我发现这两个
圆柱的半径比也是4:5,它们的体积比和半径比是相等的。
它们的体积比是几比几呢?
4厘米
5厘米
5厘米
4厘米
×4
×5
圆柱1
V圆柱1
圆柱2
V圆柱2
=
=
5
4
√
你还有什么发现吗?
两个圆柱的体积比=底面半径比=4:5
哪个圆柱的
体积大?
探索与发现2:
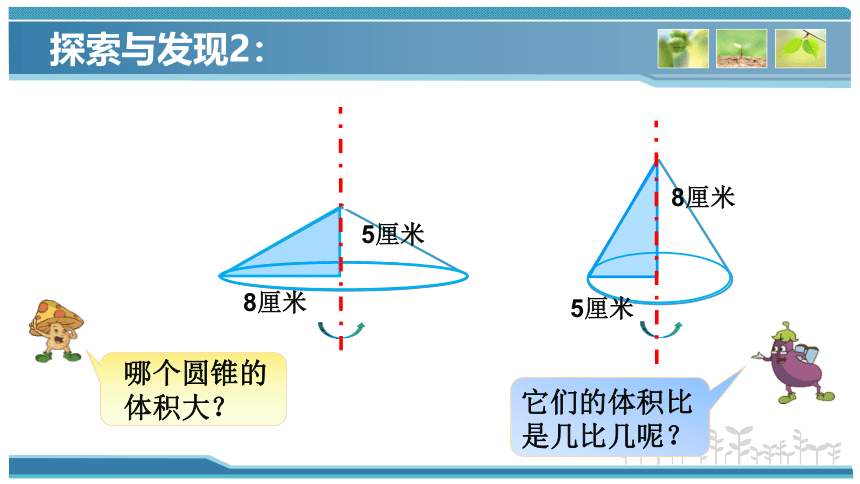
哪个圆锥的
体积大?
它们的体积比是几比几呢?
8厘米
5厘米
5厘米
8厘米
探索与发现2:
哪个圆锥的
体积大?
它们的体积比是几比几呢?
×8÷3
×5÷3
V圆锥1
V圆锥2
=
=
5
8
这两个圆锥的体积比与它们的半径比相等吗?
两个圆锥的体积比=底面半径比=8:5
圆锥2
圆锥1
√
探索与发现
通过刚才的研究,你有什么发现?
探索与发现
用同一个长方形或直角三角形绕不同的边旋转,
可以得到大小不同的圆柱或圆锥;还发现这两个
圆柱或圆锥的体积比就等于它们底面半径比。
选一张长方形纸,卷成两个大小不同的圆柱。
探索与发现3:
怎样卷圆柱的体积比较大?
它们的体积比是几比几呢?
它们的体积比与底面半径比相等吗?
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
长方形的长和宽分别对应了圆柱的什么?
20厘米
30厘米
长方形的长对应圆柱1的底面周长。
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
长方形的长和宽分别对应了圆柱的什么?
20厘米
30厘米
长方形的宽对应圆柱2的底面周长,长对应圆柱2
的高,是30厘米。
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
20厘米
30厘米
还需要知道圆柱的底面半径和高。
怎样卷圆柱的体积比较大?
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
20厘米
30厘米
我们可以根据周长比推算出半径比,
因为圆的周长都等于半径×2×π。
怎样卷圆柱的体积比较大?
探索与发现3:
把长方形的长卷成圆柱
的底面周长,这样卷圆
柱的体积比较大。
它们的体积比是几比几呢?
× 3
× 2
V圆柱1
V圆柱2
=
=
2
3
现在,你有什么发现?
两个圆柱的体积比=它们的底面半径比=3:2
圆柱2
圆柱1
2r1
C1
C2
=
=
2
3
2r2
20
h1
h2
=
=
2
3
30
√
有两个圆柱形容器,它们的高相等,底面半径的比是1:2。
探索与发现4:
它们的体积比是几比几呢?
假设法:假设两个容器的高都是10厘米,一个容器底面半径是1厘米,另一个容器底面半径是2厘米。
圆柱1
圆柱2
× 10
× 10
V圆柱1
V圆柱2
=
=
4
1
半径r 底面积s 高h 体积v
圆柱1 1
圆柱2 2
列表整理
1
1
1
1
4
4
V=Sh
我是根据圆柱体积公式进行推理。
练习与应用
8.有两个不同形状但高都是10厘米的装饰瓶,里面放满了五彩石。从里面量,圆柱形装饰瓶的底面直径是10厘米;长方体装饰瓶的长和宽都是11厘米。
哪个装饰瓶里的五彩石多一些?
8.有两个不同形状但高都是10厘米的装饰瓶,里面放满了五彩石。从里面量,圆柱形装饰瓶的底面直径是10厘米;长方体装饰瓶的长和宽都是11厘米。哪个装饰瓶里的五彩石多一些?
(10÷2) ×π×10
11×11×10=1210(立方厘米)
785 <1210
答:长方体装饰瓶里的五彩石多一些。
=25×10×π
=250π
=785(立方厘米)
练习与应用
9.一根自来水管的内直径是20毫米。如果水流的速度是0.8米/秒,这根
水管1分钟可以流出多少升水?
思路点拨:“水管1分钟可以流出多少升水”就是求什么?
答:这根水管1分钟可以流出4.8升水。
1分=60秒
20毫米=0.2分米
0.8米/秒=8分米/秒
8×60=480(分米)
4.8立方分米=4.8升
练习与应用
×480
(0.2÷2)2
=4.8(立方分米)
收获与反思
通过这节课的学习,你有哪些收获?
动手操作
善于想象
探索发现
灵活运用
课后练习
课后练习
思路点拨:
①求“沙坑里沙子的厚度是多少厘米”就是求什么呢?
②你还有什么地方需要提醒大家的?
10.一个圆锥形沙堆,底面积是24平方米,高是1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
练习与应用
方法二:
方法一:
10.一个圆锥形沙堆,底面积是24平方米,高是1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
方程法
算术法
解:设沙坑里沙子的厚度是x米。
30 x=9.6
X=0.32
h=V÷S
( ×24×1.2) ÷(7.5×4)
=9.6÷30
=0.32(米)
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
7.5×4x= ×24×1.2
练习与应用
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱。(如图)
⑴纸箱的长、宽、高至少各是多少厘米?
长:6×7=42(厘米)
宽:4×7=28(厘米)
高:12厘米
答:纸箱的长至少是42厘米;宽至少是28厘米;高至少是12厘米。
练习与应用
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱。(如图)
⑵纸箱的容积至少是多少立方厘米?
42×28×12=14112(立方厘米)
答:纸箱的容积至少是14112立方厘米。
练习与应用
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱。(如图)
⑶做一个这样的纸箱,至少要用硬纸板多少平方厘米?
(箱盖和箱底的重叠部分按2000平方厘米计算)
(42×28+42×12+28×12)×2
=(1176+504+336)×2
=2016×2
=4032(平方厘米)
4032+2000=6032(平方厘米)
答:至少要用硬纸板6032平方厘米。
练习与应用
圆柱和圆锥整理与练习(2)
课后练习
一、火眼金睛
1.从圆锥的顶点到底面上的任何一点的距离就是圆锥的高。( )
×
解析:从圆锥的顶点到底面圆心的距离是圆锥的高。
2.圆柱的底面半径扩大到原来的2倍,高不变,则侧面积扩大到原来的
4倍。 ( )
×
解析:圆柱的侧面积=底面周长×高,S侧=2πrh,当圆柱底面半径扩大到原来的2倍,高不变时,侧面积也扩大到原来的2倍。
课后练习
一、火眼金睛
3.把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。
( )
√
4.如果两个圆柱的侧面积相等,那么它们的体积也相等。 ( )
×
解析:两个圆柱的侧面积相等仅仅说明半径和高的乘积相等,但底面半径和高不一定相等,所以体积也不一定相等。
解析:把一个圆柱削成一个最大的圆锥,削成的圆锥的体积是圆柱体积的 ,
削掉部分是圆柱体积的 ,即削掉部分的体积是圆锥体积的2倍。
课后练习
5.将一个圆柱切拼成一个近似的长方体,这个长方体和原来的圆柱相比,体积不变,表面积变小。 ( )
×
解析:将一个圆柱切拼成一个近似的长方体后,体积不变,但表面积增加两个侧面,即增加了2rh。
一、火眼金睛
课后练习
1.如果一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高和它的底面直径的比是( )
A. 1:1 B. 1:π C. 2:π D. π:1
二、精准选择
解析:圆柱的侧面展开后是正方形,则圆柱的底面周长和高相等,即h=πd,则h:d=πd:d=π:1。
D
课后练习
2.一根圆柱形木料的底面直径是12厘米,高是20厘米,把它截成三段,每段都是圆柱,截成三段后表面积增加了( )平方厘米。
A.48π B. 72π C. 720π D. 144π
二、精准选择
解析:把圆柱截成三段,每段都是圆柱,表面积增加了4个底面的面积,即π×(12÷2)2×4=144π
D
课后练习
二、精准选择
A
3.小明做了一个圆柱和3个圆锥,规格如下图(单位:厘米),将圆柱里的水倒入圆锥( ),正好倒满。
解析:圆柱的底面直径为10厘米,高为18厘米,圆柱中水深6厘米,则水的体积占圆柱体积的 ;圆锥A与圆柱等底等高,则圆锥A的体积是圆柱的 ;因此,将圆柱里的水倒入圆锥A,正好倒满.
课后练习
4.下面的几何体中,( )的体积不可以用“底面积×高”求得。
A. 长方体 B. 正方体 C. 圆柱 D. 圆锥
二、精准选择
D
解析:长方体、正方体、圆柱都是直柱体,它们的体积都可以用“底面积×高”计算,圆锥的体积是与它等底等高的圆柱体积的 ,V锥= ×底面积×高。
课后练习
二、精准选择
C
解析:甲沿底面切分,增加两个底面积,即增加2πy2 ;乙沿高切分,增加两个 长为高、宽为底面直径的长方形的面积,即增加4yh。
D
5.下面是两位同学对同一个圆柱的两种不同的切分(平均分成两块)方 法。甲切分后,表面积比原来增加( );乙切分后,表面积比原来增加( )。
A. πy B. 2yh C. 2πy2 D. 4yh
探索与发现1:
4厘米
5厘米
5厘米
4厘米
哪个圆柱的
体积大?
它们的体积比是几比几呢?
探索与发现1:
我发现这两个
圆柱的半径比也是4:5,它们的体积比和半径比是相等的。
它们的体积比是几比几呢?
4厘米
5厘米
5厘米
4厘米
×4
×5
圆柱1
V圆柱1
圆柱2
V圆柱2
=
=
5
4
√
你还有什么发现吗?
两个圆柱的体积比=底面半径比=4:5
哪个圆柱的
体积大?
探索与发现2:
哪个圆锥的
体积大?
它们的体积比是几比几呢?
8厘米
5厘米
5厘米
8厘米
探索与发现2:
哪个圆锥的
体积大?
它们的体积比是几比几呢?
×8÷3
×5÷3
V圆锥1
V圆锥2
=
=
5
8
这两个圆锥的体积比与它们的半径比相等吗?
两个圆锥的体积比=底面半径比=8:5
圆锥2
圆锥1
√
探索与发现
通过刚才的研究,你有什么发现?
探索与发现
用同一个长方形或直角三角形绕不同的边旋转,
可以得到大小不同的圆柱或圆锥;还发现这两个
圆柱或圆锥的体积比就等于它们底面半径比。
选一张长方形纸,卷成两个大小不同的圆柱。
探索与发现3:
怎样卷圆柱的体积比较大?
它们的体积比是几比几呢?
它们的体积比与底面半径比相等吗?
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
长方形的长和宽分别对应了圆柱的什么?
20厘米
30厘米
长方形的长对应圆柱1的底面周长。
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
长方形的长和宽分别对应了圆柱的什么?
20厘米
30厘米
长方形的宽对应圆柱2的底面周长,长对应圆柱2
的高,是30厘米。
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
20厘米
30厘米
还需要知道圆柱的底面半径和高。
怎样卷圆柱的体积比较大?
A4纸的长大约是30厘米,宽大约是20厘米,卷成两个大小不同的圆柱。
探索与发现3:
30厘米
20厘米
圆柱1
圆柱2
20厘米
30厘米
我们可以根据周长比推算出半径比,
因为圆的周长都等于半径×2×π。
怎样卷圆柱的体积比较大?
探索与发现3:
把长方形的长卷成圆柱
的底面周长,这样卷圆
柱的体积比较大。
它们的体积比是几比几呢?
× 3
× 2
V圆柱1
V圆柱2
=
=
2
3
现在,你有什么发现?
两个圆柱的体积比=它们的底面半径比=3:2
圆柱2
圆柱1
2r1
C1
C2
=
=
2
3
2r2
20
h1
h2
=
=
2
3
30
√
有两个圆柱形容器,它们的高相等,底面半径的比是1:2。
探索与发现4:
它们的体积比是几比几呢?
假设法:假设两个容器的高都是10厘米,一个容器底面半径是1厘米,另一个容器底面半径是2厘米。
圆柱1
圆柱2
× 10
× 10
V圆柱1
V圆柱2
=
=
4
1
半径r 底面积s 高h 体积v
圆柱1 1
圆柱2 2
列表整理
1
1
1
1
4
4
V=Sh
我是根据圆柱体积公式进行推理。
练习与应用
8.有两个不同形状但高都是10厘米的装饰瓶,里面放满了五彩石。从里面量,圆柱形装饰瓶的底面直径是10厘米;长方体装饰瓶的长和宽都是11厘米。
哪个装饰瓶里的五彩石多一些?
8.有两个不同形状但高都是10厘米的装饰瓶,里面放满了五彩石。从里面量,圆柱形装饰瓶的底面直径是10厘米;长方体装饰瓶的长和宽都是11厘米。哪个装饰瓶里的五彩石多一些?
(10÷2) ×π×10
11×11×10=1210(立方厘米)
785 <1210
答:长方体装饰瓶里的五彩石多一些。
=25×10×π
=250π
=785(立方厘米)
练习与应用
9.一根自来水管的内直径是20毫米。如果水流的速度是0.8米/秒,这根
水管1分钟可以流出多少升水?
思路点拨:“水管1分钟可以流出多少升水”就是求什么?
答:这根水管1分钟可以流出4.8升水。
1分=60秒
20毫米=0.2分米
0.8米/秒=8分米/秒
8×60=480(分米)
4.8立方分米=4.8升
练习与应用
×480
(0.2÷2)2
=4.8(立方分米)
收获与反思
通过这节课的学习,你有哪些收获?
动手操作
善于想象
探索发现
灵活运用
课后练习
课后练习
思路点拨:
①求“沙坑里沙子的厚度是多少厘米”就是求什么呢?
②你还有什么地方需要提醒大家的?
10.一个圆锥形沙堆,底面积是24平方米,高是1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
练习与应用
方法二:
方法一:
10.一个圆锥形沙堆,底面积是24平方米,高是1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
方程法
算术法
解:设沙坑里沙子的厚度是x米。
30 x=9.6
X=0.32
h=V÷S
( ×24×1.2) ÷(7.5×4)
=9.6÷30
=0.32(米)
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
7.5×4x= ×24×1.2
练习与应用
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱。(如图)
⑴纸箱的长、宽、高至少各是多少厘米?
长:6×7=42(厘米)
宽:4×7=28(厘米)
高:12厘米
答:纸箱的长至少是42厘米;宽至少是28厘米;高至少是12厘米。
练习与应用
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱。(如图)
⑵纸箱的容积至少是多少立方厘米?
42×28×12=14112(立方厘米)
答:纸箱的容积至少是14112立方厘米。
练习与应用
11.一种圆柱形饮料罐,底面直径是7厘米,高是12厘米。将24罐这种饮料放入一个长方体纸箱。(如图)
⑶做一个这样的纸箱,至少要用硬纸板多少平方厘米?
(箱盖和箱底的重叠部分按2000平方厘米计算)
(42×28+42×12+28×12)×2
=(1176+504+336)×2
=2016×2
=4032(平方厘米)
4032+2000=6032(平方厘米)
答:至少要用硬纸板6032平方厘米。
练习与应用
