沪科版数学七年级下6.2.1实数课件 (共18张PPT)
文档属性
| 名称 | 沪科版数学七年级下6.2.1实数课件 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
6.2 实数(第一课时)
沪科版数学七年级下
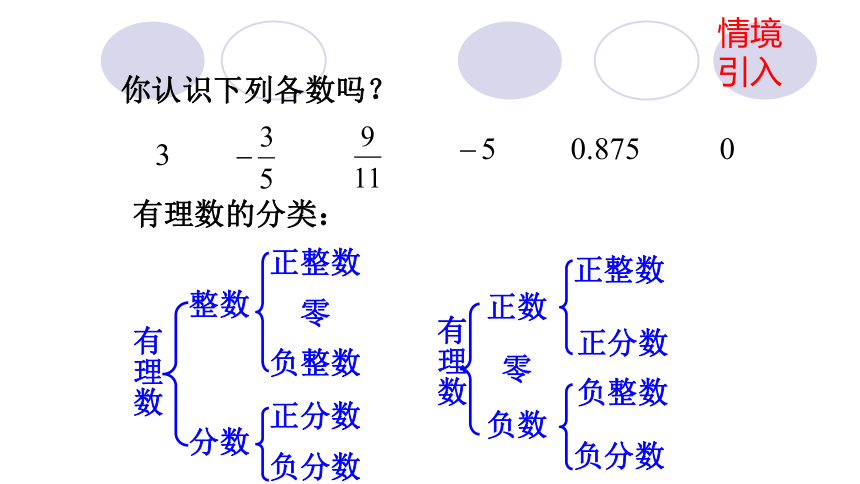
你认识下列各数吗?
有理数的分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正数
负数
正整数
零
负整数
正分数
负分数
情境引入
在数轴上表示下列各数:
-3 -2 -1 0 1 2 3 4
有理数都可以用数轴上的点表示.
它们是正确的吗?
-4是16的平方根
16的平方根是4与-4
平方根等于本身的数1,0
算术平方根等于本身的数是1
3的算术平方根记作
把下列各数写成小数的形式:
整数和分数统称为有理数
有限小数
无限循环小数
有限小数和无限循环小数叫有理数
新知探究
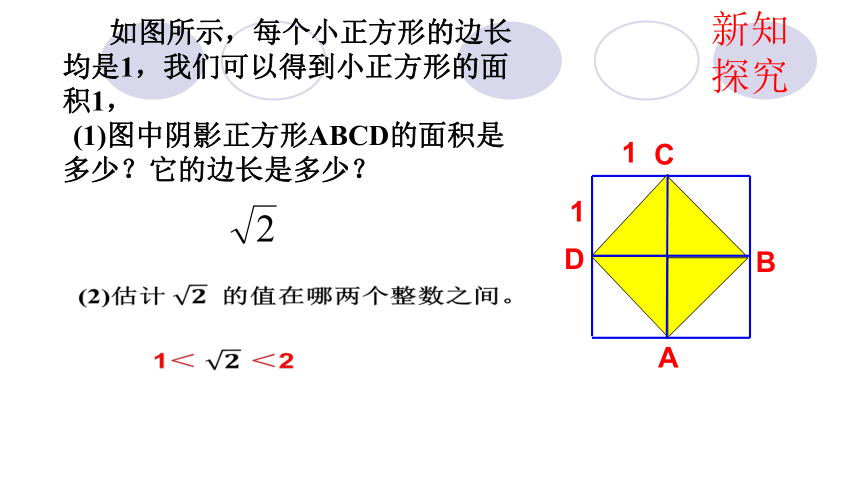
如图所示,每个小正方形的边长均是1,我们可以得到小正方形的面积1,
(1)图中阴影正方形ABCD的面积是多少?它的边长是多少?
1< <2
新知探究
(2)估计 的值在哪两个整数之间。
1
1
A
B
C
D
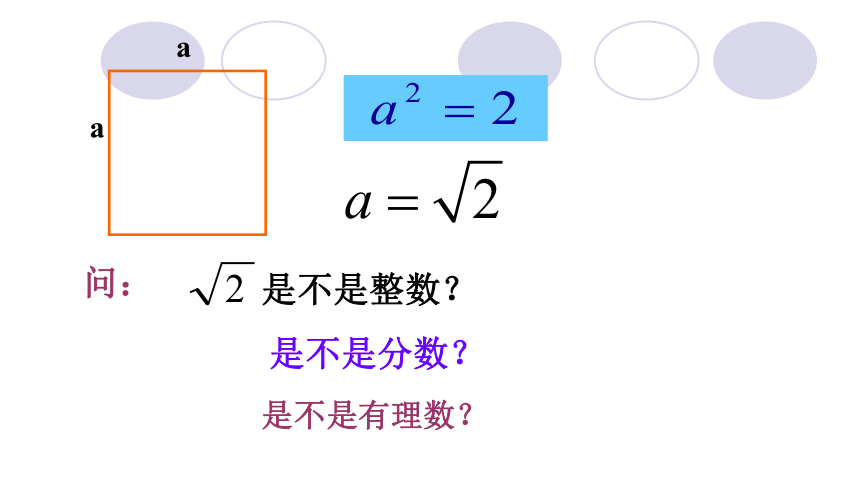
是不是有理数?
a
a
是不是整数?
是不是分数?
问:
有多大
12=1, ( )2=2, 22=4
1.412=1.9881, ( )2=2, 1.422=2.0164
1.41< <1.42
1.42=1.96 ( )2=2, 1.52=2.25
1.4< <1.5
1< < 2
=1.
=1.4
=1.41
用这种方法可以得到一系列越来越接近 的 近似值。
有多大呢?
你以前见过这种数吗?
无限不循环小数叫做无理数
——无理数
无理数的三种形式
2 ). π, -π…
1).
3). 0.101001000…(两个“1”之间依次多一个0),
-7.2121121112… (两个“2”之间依次多一个1)
小数的分类:
有限小数
无限小数
无限循环小数
无限不循环小数
不可化为分数
有理数
(均可化为分数)
是一个无限不循环小数,因此它不是一个有理数,是无理数
有理数和无理数统称实数.
实数定义:
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
实数分类
(无限不循环小数)
(有限小数或无限循环小数)
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
按定义分类:
分数
整数
开方开不尽的数
有规律但不循环的数
含有π 的数
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
0
正实数
负实数
例1、在 中,
属于有理数的:
属于无理数的:
属于实数的有:
例题讲解
把下列各数填入相应的集合内.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
不是带根号的都是无理数
课堂练习1
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
课堂练习2
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
有理数和无理数统称为实数.
或 有理数
整数
分数
(无限不循环小数)
(有限小数或
无限循环小数)
课堂小结
6.2 实数(第一课时)
沪科版数学七年级下
你认识下列各数吗?
有理数的分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正数
负数
正整数
零
负整数
正分数
负分数
情境引入
在数轴上表示下列各数:
-3 -2 -1 0 1 2 3 4
有理数都可以用数轴上的点表示.
它们是正确的吗?
-4是16的平方根
16的平方根是4与-4
平方根等于本身的数1,0
算术平方根等于本身的数是1
3的算术平方根记作
把下列各数写成小数的形式:
整数和分数统称为有理数
有限小数
无限循环小数
有限小数和无限循环小数叫有理数
新知探究
如图所示,每个小正方形的边长均是1,我们可以得到小正方形的面积1,
(1)图中阴影正方形ABCD的面积是多少?它的边长是多少?
1< <2
新知探究
(2)估计 的值在哪两个整数之间。
1
1
A
B
C
D
是不是有理数?
a
a
是不是整数?
是不是分数?
问:
有多大
12=1, ( )2=2, 22=4
1.412=1.9881, ( )2=2, 1.422=2.0164
1.41< <1.42
1.42=1.96 ( )2=2, 1.52=2.25
1.4< <1.5
1< < 2
=1.
=1.4
=1.41
用这种方法可以得到一系列越来越接近 的 近似值。
有多大呢?
你以前见过这种数吗?
无限不循环小数叫做无理数
——无理数
无理数的三种形式
2 ). π, -π…
1).
3). 0.101001000…(两个“1”之间依次多一个0),
-7.2121121112… (两个“2”之间依次多一个1)
小数的分类:
有限小数
无限小数
无限循环小数
无限不循环小数
不可化为分数
有理数
(均可化为分数)
是一个无限不循环小数,因此它不是一个有理数,是无理数
有理数和无理数统称实数.
实数定义:
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
实数分类
(无限不循环小数)
(有限小数或无限循环小数)
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
按定义分类:
分数
整数
开方开不尽的数
有规律但不循环的数
含有π 的数
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
0
正实数
负实数
例1、在 中,
属于有理数的:
属于无理数的:
属于实数的有:
例题讲解
把下列各数填入相应的集合内.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
不是带根号的都是无理数
课堂练习1
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
课堂练习2
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
有理数和无理数统称为实数.
或 有理数
整数
分数
(无限不循环小数)
(有限小数或
无限循环小数)
课堂小结
