沪科版数学七年级下7.3.2一元一次不等式组 课件(共21张PPT)
文档属性
| 名称 | 沪科版数学七年级下7.3.2一元一次不等式组 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
7.3 一元一次不等式组
沪科版数学七年级下
第二课时
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
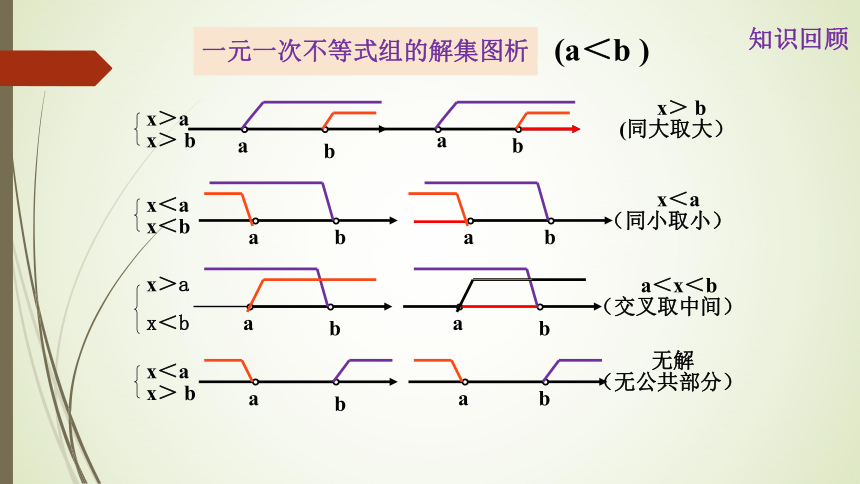
x>a
x> b
x<a
x<b
x<a
x> b
x>a
x<b
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
x> b
(同大取大)
x<a
(同小取小)
a<x<b
(交叉取中间)
无解
(无公共部分)
一元一次不等式组的解集图析
(a<b )
知识回顾
例4.解不等式:
1)
2≤3x-7<8
3)
2)
(2x-3)(x+1)<0
4)
5)
(2x-1)(x+3)>0
6)
例题讲解
(1)2≤3x-7<8
解:整理不等式为
2≤3x-7 (1)
3x-7<8 (1)
解法一
解不等式(1)得:
X≥3
解不等式(2)得:
X<5
3≤x<5
∴ 不等式组的解集为:
变为不等式组
2≤3x-7<8
2+7≤3x-7+7<8+7
9≤3x<15
3≤x<5
解法二:
利用不等式性质
解: 不等式两边同时加上7
不等式两边同时除以3
9÷3≤3x÷3<15÷3
解法一
解不等式①得:
解不等式②得:
∴ 不等式组的解集为:
变为不等式组
解:整理不等式为
解法二:
∴ 不等式组的解集为:
利用不等式性质
-9≤2x-1<15
-8≤2x<16
-4≤x<8
不等式两边同时加上1
不等式两边同时除以2
解:不等式两边同时乘以3
利用不等式性质
(2x-3)(x+1)<0
4)
解:整理不等式为
2x-3>0
x+1<0
或
2x-3<0
x+1>0
两数相乘。同号得正,异号得负
解不等式组
2x-3>0
x+1<0
x>
x<-1
得:
∴此不等式组无解
解不等式组
2x-3<0
x+1>0
X<
X>-1
得:
∴此不等式组解集 -1<x<
∴原不等式解集 -1<x<
5)
(2x-1)(x+3)>0
解:整理不等式为
2x-1>0
x+3>0
或
2x-1<0
x+3<0
两数相乘,同号得正,异号得负
解不等式组
x>
X>-3
得:
∴此不等式组解集:x>
解不等式组
2x-1<0
x+3<0
X<
X<-3
得:
∴此不等式组解集 x<
∴原不等式解集:
2x-1>0
x+3>0
x>
x<
或
6)
两数相除,同号得正,异号得负
解:整理不等式为
x-1≥0
x+2>0
或
x-1≤0
x+2<0
解不等式组
x-1≥0
x+2>0
X≥
X>-2
得:
∴此不等式组解集:x≥
x-1≤0
x+2<0
解不等式组
X≤
X<-2
得:
∴此不等式组解集:X<-2
∴原不等式解集:
X≥3
x<
或
注意:
分母不能为零
0 m 1 2
有解,则m的取值范围是______.
解:化简不等式组得
根据不等式组解集的规律,得
∵不等式组有解,
∴ m≤ x ≤
这中间的m当作数轴上的一个已知数
例2、若关于 x的不等式组
3-2x≥0
X≥m
X≤
X≥m
∴ m ≤
m ≤
例题讲解
例3、(1)若不等式组
的解集是-1<x<2,则m=____,n=____.
①
②
解: 解不等式①,得,x>m-2
解不等式②,得,x < n + 1
因为不等式组有解,所以
m-2 <x< n + 1
又因为 -1<x<2
∴ m=1 , n=1
-1 2
< x <
m-2
n + 1
∴ m-2= -1 , n + 1 = 2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
1
1
例题讲解
这里是一个含x、y的二元一次不等式组,将m看作已知数,求方程组的解集
例题讲解
1、已知关于x的不等式组
的解集为3≤x<5,
求的值
解: 解不等式①,得,x≥m+n
解不等式②,得,x < (2n+m+1)
∵不等式组有解,
∴ m+n≤ x < ( 2n+m+1 )
又 ∵3≤x<5
解得
∴ =4
这里也是一个含x的一元一次不等式,将m,n看作两个已知数
巩固练习
∵ -1∴a=1,b= - 2
∴ =1, 2b+3= -1
∴(a+1)(b-1)= - 6
巩固练习
2、已知不等式组 的解集
为-1<x<1,则(a+1)(b-1)的值为多少
2X-a<
X-2b>3
解:由题意,得不等式组的解集
2b+3< x <
1、已知关于x不等式组
无解,则a的取值范围是 ___
2、若不等式组
有解,则m的取值范围是__________.
3、关于x的不等式组
的解集为x>3,则a的取值范围是( ).
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
A
m ≥1.5
a>3
提升练习1
完成下列填空
已知关于x不等式组
无解,则a的取值范围是____
解:将x>-1,x<2在数轴上表示出来为
要使方程无解,则a不能在-1的右边,即a≤-1
-1 2
提升练习2
a≤-1
x满足不等式组
{
3x - 6 ≤2x-4
x - a >0
且x可取2个正整数解,a的取值为_ __
强化 练习1
②
①
解:解不等式①,得 x <2
解不等式②,得 x > a
a
2
∵x可取2个正整数解
∴a的取值范围是:-1≤a<0
1
0
-1
加油!
0
1
2
3
-1
m
则m的取值范围是 .
若不等式组 的解是x>2,
x >m
x >2
{
m≤2
强化练习2
课堂小结
1.关键概念:
一元一次不等式组;不等式组的解集.
2.学法指导:
数形结合法,依靠数轴求不等式组的解集.
会运用不等式组的知识解决实际问题,并注意检验结果的合理性.
7.3 一元一次不等式组
沪科版数学七年级下
第二课时
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
x>a
x> b
x<a
x<b
x<a
x> b
x>a
x<b
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
b
x> b
(同大取大)
x<a
(同小取小)
a<x<b
(交叉取中间)
无解
(无公共部分)
一元一次不等式组的解集图析
(a<b )
知识回顾
例4.解不等式:
1)
2≤3x-7<8
3)
2)
(2x-3)(x+1)<0
4)
5)
(2x-1)(x+3)>0
6)
例题讲解
(1)2≤3x-7<8
解:整理不等式为
2≤3x-7 (1)
3x-7<8 (1)
解法一
解不等式(1)得:
X≥3
解不等式(2)得:
X<5
3≤x<5
∴ 不等式组的解集为:
变为不等式组
2≤3x-7<8
2+7≤3x-7+7<8+7
9≤3x<15
3≤x<5
解法二:
利用不等式性质
解: 不等式两边同时加上7
不等式两边同时除以3
9÷3≤3x÷3<15÷3
解法一
解不等式①得:
解不等式②得:
∴ 不等式组的解集为:
变为不等式组
解:整理不等式为
解法二:
∴ 不等式组的解集为:
利用不等式性质
-9≤2x-1<15
-8≤2x<16
-4≤x<8
不等式两边同时加上1
不等式两边同时除以2
解:不等式两边同时乘以3
利用不等式性质
(2x-3)(x+1)<0
4)
解:整理不等式为
2x-3>0
x+1<0
或
2x-3<0
x+1>0
两数相乘。同号得正,异号得负
解不等式组
2x-3>0
x+1<0
x>
x<-1
得:
∴此不等式组无解
解不等式组
2x-3<0
x+1>0
X<
X>-1
得:
∴此不等式组解集 -1<x<
∴原不等式解集 -1<x<
5)
(2x-1)(x+3)>0
解:整理不等式为
2x-1>0
x+3>0
或
2x-1<0
x+3<0
两数相乘,同号得正,异号得负
解不等式组
x>
X>-3
得:
∴此不等式组解集:x>
解不等式组
2x-1<0
x+3<0
X<
X<-3
得:
∴此不等式组解集 x<
∴原不等式解集:
2x-1>0
x+3>0
x>
x<
或
6)
两数相除,同号得正,异号得负
解:整理不等式为
x-1≥0
x+2>0
或
x-1≤0
x+2<0
解不等式组
x-1≥0
x+2>0
X≥
X>-2
得:
∴此不等式组解集:x≥
x-1≤0
x+2<0
解不等式组
X≤
X<-2
得:
∴此不等式组解集:X<-2
∴原不等式解集:
X≥3
x<
或
注意:
分母不能为零
0 m 1 2
有解,则m的取值范围是______.
解:化简不等式组得
根据不等式组解集的规律,得
∵不等式组有解,
∴ m≤ x ≤
这中间的m当作数轴上的一个已知数
例2、若关于 x的不等式组
3-2x≥0
X≥m
X≤
X≥m
∴ m ≤
m ≤
例题讲解
例3、(1)若不等式组
的解集是-1<x<2,则m=____,n=____.
①
②
解: 解不等式①,得,x>m-2
解不等式②,得,x < n + 1
因为不等式组有解,所以
m-2 <x< n + 1
又因为 -1<x<2
∴ m=1 , n=1
-1 2
< x <
m-2
n + 1
∴ m-2= -1 , n + 1 = 2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
1
1
例题讲解
这里是一个含x、y的二元一次不等式组,将m看作已知数,求方程组的解集
例题讲解
1、已知关于x的不等式组
的解集为3≤x<5,
求的值
解: 解不等式①,得,x≥m+n
解不等式②,得,x < (2n+m+1)
∵不等式组有解,
∴ m+n≤ x < ( 2n+m+1 )
又 ∵3≤x<5
解得
∴ =4
这里也是一个含x的一元一次不等式,将m,n看作两个已知数
巩固练习
∵ -1
∴ =1, 2b+3= -1
∴(a+1)(b-1)= - 6
巩固练习
2、已知不等式组 的解集
为-1<x<1,则(a+1)(b-1)的值为多少
2X-a<
X-2b>3
解:由题意,得不等式组的解集
2b+3< x <
1、已知关于x不等式组
无解,则a的取值范围是 ___
2、若不等式组
有解,则m的取值范围是__________.
3、关于x的不等式组
的解集为x>3,则a的取值范围是( ).
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
A
m ≥1.5
a>3
提升练习1
完成下列填空
已知关于x不等式组
无解,则a的取值范围是____
解:将x>-1,x<2在数轴上表示出来为
要使方程无解,则a不能在-1的右边,即a≤-1
-1 2
提升练习2
a≤-1
x满足不等式组
{
3x - 6 ≤2x-4
x - a >0
且x可取2个正整数解,a的取值为_ __
强化 练习1
②
①
解:解不等式①,得 x <2
解不等式②,得 x > a
a
2
∵x可取2个正整数解
∴a的取值范围是:-1≤a<0
1
0
-1
加油!
0
1
2
3
-1
m
则m的取值范围是 .
若不等式组 的解是x>2,
x >m
x >2
{
m≤2
强化练习2
课堂小结
1.关键概念:
一元一次不等式组;不等式组的解集.
2.学法指导:
数形结合法,依靠数轴求不等式组的解集.
会运用不等式组的知识解决实际问题,并注意检验结果的合理性.
