青岛版小学三年级数学下册《不进位乘法笔算(信息窗2)》教学设计
文档属性
| 名称 | 青岛版小学三年级数学下册《不进位乘法笔算(信息窗2)》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-02 00:00:00 | ||
图片预览


文档简介
《美丽的街景——两位数乘两位数》教学设计
教学内容:教科书第26~27页,两位数乘两位数(不进位)。
教学目标:
1.充分体验解决不进位的两位数乘两位数计算的过程和形成竖式的过程,借助数形结合直观感受算理,能正确地计算。
2.感悟蕴含于两位数乘两位数计算过程中的数学思想方法。
3.主动参与新知识的探究活动,能够有条理地表述自己的想法,学会有序的思考,培养学生的合作意识,评价意识及良好的学习习惯。
教学过程:
活动一:数形结合,提高估算能力。
1.导入新课,提出问题。
(出示一幅硬笔书法作品。)
师:看到这幅书法作品,你能提出什么数学问题?
生:一共有多少个字?
师:那要解决这个问题需要知道哪些条件?
生:一行有多少个字,一共有这样的多少行。
师生共同数一数一行的字数和行数——一行有23个字;有12行。
师:要求一共有多少个字应该怎样列算式?
生:23×12。
师:为什么用乘法?
生:每行23个,12行,也就是求12个23是多少;所以用23×12。
【设计意图:让学生根据实际情境自主提出问题,并找出解决问题所需要的条件,较好的培养了学生的数学问题意识,同时对乘法的意义进行了巩固复习。】
2.进行估算,培养估算意识。
师:孩子们,你觉得,这幅作品大约一共有多少个字?来,结合算式估一估。
生l:大约有200个。
师:说说你的想法。
生:把23估成20,把12估成10,20×10=200。
师:20×10=200这个结果,比实际结果,大了还是小了?为什么?
生:小了。因为把因数估小了,所以乘积也就小了。
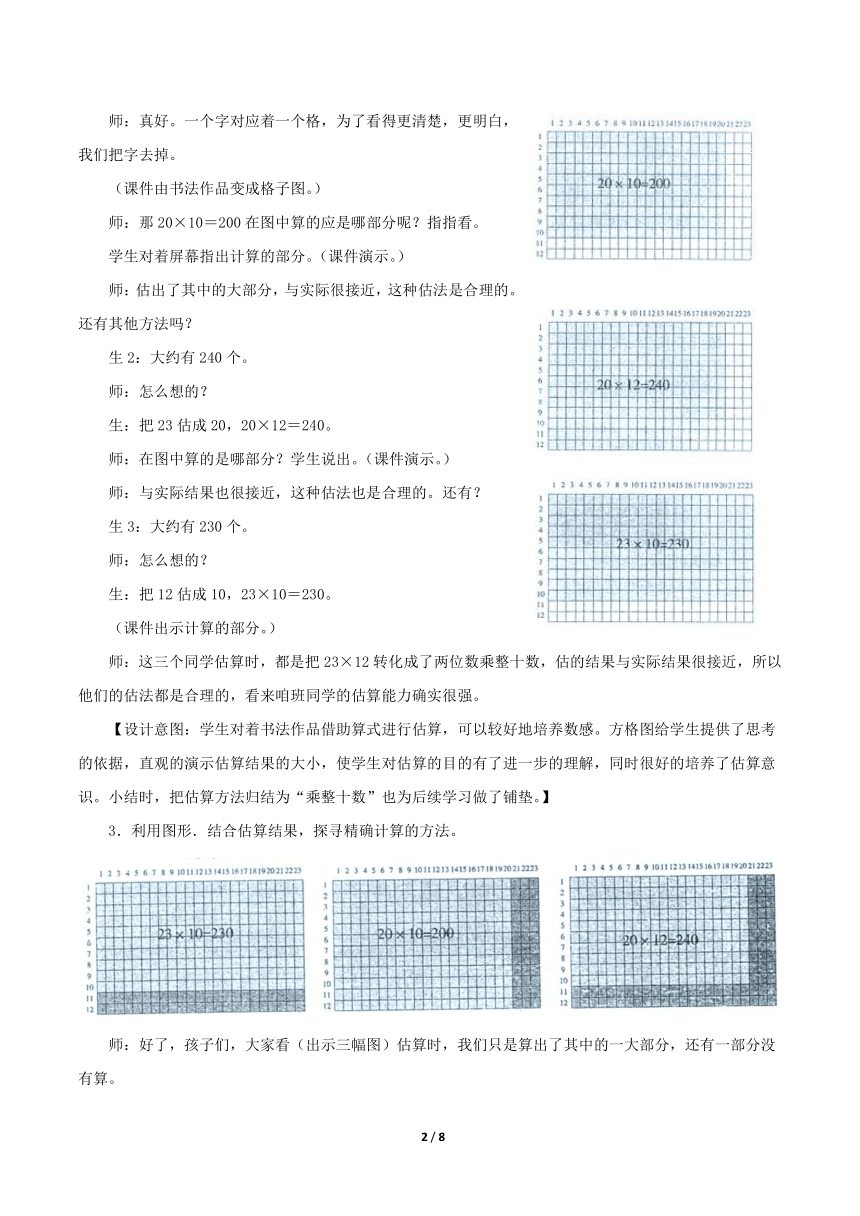
师:真好。一个字对应着一个格,为了看得更清楚,更明白,我们把字去掉。
(课件由书法作品变成格子图。)
师:那20×10=200在图中算的应是哪部分呢?指指看。
学生对着屏幕指出计算的部分。(课件演示。)
师:估出了其中的大部分,与实际很接近,这种估法是合理的。还有其他方法吗?
生2:大约有240个。
师:怎么想的?
生:把23估成20,20×12=240。
师:在图中算的是哪部分?学生说出。(课件演示。)
师:与实际结果也很接近,这种估法也是合理的。还有?
生3:大约有230个。
师:怎么想的?
生:把12估成10,23×10=230。
(课件出示计算的部分。)
师:这三个同学估算时,都是把23×12转化成了两位数乘整十数,估的结果与实际结果很接近,所以他们的估法都是合理的,看来咱班同学的估算能力确实很强。
【设计意图:学生对着书法作品借助算式进行估算,可以较好地培养数感。方格图给学生提供了思考的依据,直观的演示估算结果的大小,使学生对估算的目的有了进一步的理解,同时很好的培养了估算意识。小结时,把估算方法归结为“乘整十数”也为后续学习做了铺垫。】
3.利用图形.结合估算结果,探寻精确计算的方法。
师:好了,孩子们,大家看(出示三幅图)估算时,我们只是算出了其中的一大部分,还有一部分没有算。
那到底一共有多少个字呢?你觉得可以怎样做?
生1:用估算的那部分,加上还没有估的那部分。
生2:用已经算的那部分,加上没算的那部分。
【设计意图:利用方格图的直观呈现,进行估算结果与实际结果的对比,使学生深刻理解,估算结果只是实际结果的一部分,还有一部分没有算,进而初步构建计算准确结果的模型。】
活动二:探究精算方法,渗透数学思想。
师:下面我们就用这种方法,列式计算一下。
听要求:同位合作,从三种思路中选取一种,在图的右边列式计算出一共有多少字。
小组合作,教师巡视指导。进行方法交流展示。
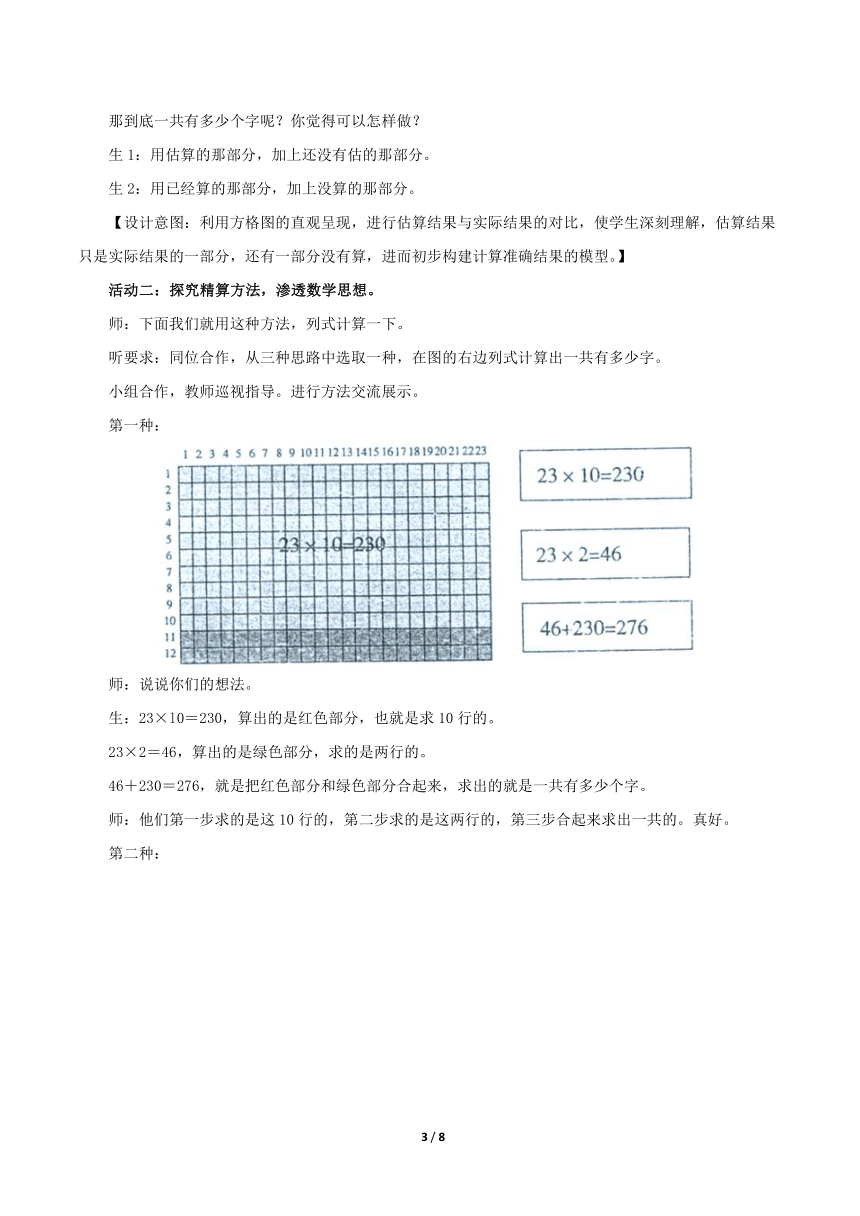
第一种:
师:说说你们的想法。
生:23×l0=230,算出的是红色部分,也就是求10行的。
23×2=46,算出的是绿色部分,求的是两行的。
46+230=276,就是把红色部分和绿色部分合起来,求出的就是一共有多少个字。
师:他们第一步求的是这10行的,第二步求的是这两行的,第三步合起来求出一共的。真好。
第二种:
师:谁来说说,他们每一步求的是什么?
生1:第一步求的是红色部分。
生2:第二步求的是绿色部分。
生3:第三步合起来求出一共的。
师:他也是分了三步,第一步算出左边这一大部分,第二步算出右边这一部分,第三步合起来。也很好!
师:大家看,23×12,以前我们不会计算,但是咱们大家把它变了变,变成了已学的两位数乘整十数、两位数乘一位数。把没学的变成已经学习的来解决。咱班同学真会思考,其实大家刚才用的方法,就是数学中常说的“转化”。这种方法在以后的学习中,我们会经常用到。
【设计意图:通过给学生创设广阔的思维空间,让学生利用自主创造出来的思路,小组合作探究,找出不同思路下解决问题的方法;很好地培养了学生的思维能力和解决问题的能力,以及小组合作的能力,对后续竖式算理的理解做好了铺垫。】
活动三:尝试列竖式,明确算理和算法。
师:刚才我们是利用口算的方法计算出23×12的结果是276,那还可以怎样做?
生:列竖式。
师:怎样列竖式呢?
大家看,刚才我们借助方格图,分三步求出一共有276个字。那你们能不能用竖式把这三步过程清楚地表示出来呢?
来,试试看。
学生独立完成,教师巡视指导。交流展示。
第一种:
师:说说你的想法。
生:第一步23×2=46,算的是绿色部分;第二步23×10=230,算的是红色部;第三步46+230=276,就是把两部分合起来,求出一共的。
师:他用三个竖式分三步计算出结果,把刚才的过程很好地表示出来了。很好。
第二种:
师:他把三个竖式合在一起了,用一个竖式来表示。谁来说说,他分了几步来完成的?
生1:分三步完成的。
师:是哪三步?
生2:第一步是23×2=46,第二步是23×10=230,第三步是46+230=276。
师:他用一个竖式就计算出了结果,非常好。
第三种:
师:比较一下刚才的方法和这种方法,有没有什么不同?
生:这种方法没写加号,23后面没写0。
师:哦,计算过程是,一样的,只是没写加号和0;我们先来看,23后面不写O,行不行?
生:行。
师:为什么?
生1:因为23乘十位上的1,得到的是23个十,也就是230,所以那个O可以不写。
师:确实,O写上是对的,不写也是对的。
师:O的问题解决了。我们再来看这个加号,可以不写吗?为什么?
生:可以。写上,表示的是把上下两部分合起来;不写,表示的也是把那两个数合起来。
师:哦,写不写表示的含义都是一样的,所以,加号可以写,也可以不写。这种写法,省了0和加号更简单了。
【设计意图:让学生亲身经历由三步横式到竖式,竖式由分别列出的三个竖式,到整合在一起的一个竖式,最后到规范的简化竖式。这里通过这个过程促使学生明白知识间的联系,在理解算理的基础上,深刻感悟出计算中每步简化的优越性;同时让学生学会交流,学会分享,在交流中体验算法多样化,欣赏别人的长处。】
师:看来啊,我们用一个竖式就可以计算出23×12的结果,我们一起来写一下。
先写:23乘l2,要把相同数位对齐。
师:乘的时候,其实就是把l2分成lO和2。通常情况下,我们先乘个位(遮住十位上的1)。
先算23×2,算出两行的。
再算(遮住个位上的2)23乘十位上的1,得23个十,O可以省略不写。2写在百位,3写在十位,一定要把数位对齐。算出这10行的。
然后把这两部分加起来。是276。
师:好了,大家看,开始的时候,我们是用三步,计算出276。(指着竖式。)现在,也是用这三步。虽然书写方式不同,但是道理却一样的。用竖式来计算,更清楚,更便捷了。以后,我们计算两位数乘两位数,就可以用竖式来进行计算。
【设计意图:通过对竖式的规范整理,借助方格图,使数和形有机结合,化抽象为形象,使学生对算理的理解从纯粹的数据分析中走出来,变得有“形”可依。进而,在学生头脑中建立起清晰的三步有序过程,使他们对竖式每一步的理解就不再仅仅是一种计算程序,而是活生生的直观再现。这样学生就充分地体验了由抽象算理到直观算法的过渡和演绎过程,进而达到对算理的深刻理解和对算法的真正掌握。】
活动四:巩固练习。
师:我们做个题目试试,好吗?
1.仿例练习。
师:拿出3号题卡,完成第一题中的两个题目。巡视时,可以提示:有困难的同学,可以像刚才老师那样,把不算的那个数字先遮住。
学生独立完成。
师:多数同学已经完成了,我们一起来看一下。
第1题,第一步算的是:42×2.填84;第二步算的是42×l,表示42个十,也就是420。
那第一步算出的,在图中,就是算出几行的?第二步呢?
师:再看这个012×24,来说一下——第一步算的是?第二步呢?,第三步?你们填对了吗?
大家想一想,如果这里有一个长方形,每行有12个,有这样的24行,第一步算出的几行的?第二步呢?第三步是把4行的和20行的合起来。
师:看来咱们同学已经掌握了两位数乘两位数的方法。再看第二题。
2.火眼金睛辨对错。
师:仔细观察,看看问题出在哪儿?说说吧。
师:第二个43表示的是430,3应该对齐十位。
师:我们在列竖式计算时,需要注意什么啊?一定要把数位对齐。
师:你们记住了?请完成题卡中的“列竖式计算”。
3.竖式计算:23×21。
师:说说怎样想的?第一步算的是23×l,第二步算的是23×20,第三步加起来。
师:看来咱们大家不但会算,还明白了其中的道理。真不错。
活动五:总结反思。
师:一节课马上就要结束了,谁来谈谈你这节课都有哪些收获?
(数学知识方面的:两位数乘两位数的计算,会列竖式计算两位数乘两位数等。)
师:其实我们还有一个收获,那就是在遇到新问题的时候,可以把它转化成已学的知识来解决。有时我们还可以利用图形来帮忙。
师:最后,老师给大家一个建议,课后利用本节课的收获?解决一下三位数乘两位数和三位数乘三位数的问题。相信你们一定能行的。这节课我们就上到这,下课。
1 / 8
教学内容:教科书第26~27页,两位数乘两位数(不进位)。
教学目标:
1.充分体验解决不进位的两位数乘两位数计算的过程和形成竖式的过程,借助数形结合直观感受算理,能正确地计算。
2.感悟蕴含于两位数乘两位数计算过程中的数学思想方法。
3.主动参与新知识的探究活动,能够有条理地表述自己的想法,学会有序的思考,培养学生的合作意识,评价意识及良好的学习习惯。
教学过程:
活动一:数形结合,提高估算能力。
1.导入新课,提出问题。
(出示一幅硬笔书法作品。)
师:看到这幅书法作品,你能提出什么数学问题?
生:一共有多少个字?
师:那要解决这个问题需要知道哪些条件?
生:一行有多少个字,一共有这样的多少行。
师生共同数一数一行的字数和行数——一行有23个字;有12行。
师:要求一共有多少个字应该怎样列算式?
生:23×12。
师:为什么用乘法?
生:每行23个,12行,也就是求12个23是多少;所以用23×12。
【设计意图:让学生根据实际情境自主提出问题,并找出解决问题所需要的条件,较好的培养了学生的数学问题意识,同时对乘法的意义进行了巩固复习。】
2.进行估算,培养估算意识。
师:孩子们,你觉得,这幅作品大约一共有多少个字?来,结合算式估一估。
生l:大约有200个。
师:说说你的想法。
生:把23估成20,把12估成10,20×10=200。
师:20×10=200这个结果,比实际结果,大了还是小了?为什么?
生:小了。因为把因数估小了,所以乘积也就小了。
师:真好。一个字对应着一个格,为了看得更清楚,更明白,我们把字去掉。
(课件由书法作品变成格子图。)
师:那20×10=200在图中算的应是哪部分呢?指指看。
学生对着屏幕指出计算的部分。(课件演示。)
师:估出了其中的大部分,与实际很接近,这种估法是合理的。还有其他方法吗?
生2:大约有240个。
师:怎么想的?
生:把23估成20,20×12=240。
师:在图中算的是哪部分?学生说出。(课件演示。)
师:与实际结果也很接近,这种估法也是合理的。还有?
生3:大约有230个。
师:怎么想的?
生:把12估成10,23×10=230。
(课件出示计算的部分。)
师:这三个同学估算时,都是把23×12转化成了两位数乘整十数,估的结果与实际结果很接近,所以他们的估法都是合理的,看来咱班同学的估算能力确实很强。
【设计意图:学生对着书法作品借助算式进行估算,可以较好地培养数感。方格图给学生提供了思考的依据,直观的演示估算结果的大小,使学生对估算的目的有了进一步的理解,同时很好的培养了估算意识。小结时,把估算方法归结为“乘整十数”也为后续学习做了铺垫。】
3.利用图形.结合估算结果,探寻精确计算的方法。
师:好了,孩子们,大家看(出示三幅图)估算时,我们只是算出了其中的一大部分,还有一部分没有算。
那到底一共有多少个字呢?你觉得可以怎样做?
生1:用估算的那部分,加上还没有估的那部分。
生2:用已经算的那部分,加上没算的那部分。
【设计意图:利用方格图的直观呈现,进行估算结果与实际结果的对比,使学生深刻理解,估算结果只是实际结果的一部分,还有一部分没有算,进而初步构建计算准确结果的模型。】
活动二:探究精算方法,渗透数学思想。
师:下面我们就用这种方法,列式计算一下。
听要求:同位合作,从三种思路中选取一种,在图的右边列式计算出一共有多少字。
小组合作,教师巡视指导。进行方法交流展示。
第一种:
师:说说你们的想法。
生:23×l0=230,算出的是红色部分,也就是求10行的。
23×2=46,算出的是绿色部分,求的是两行的。
46+230=276,就是把红色部分和绿色部分合起来,求出的就是一共有多少个字。
师:他们第一步求的是这10行的,第二步求的是这两行的,第三步合起来求出一共的。真好。
第二种:
师:谁来说说,他们每一步求的是什么?
生1:第一步求的是红色部分。
生2:第二步求的是绿色部分。
生3:第三步合起来求出一共的。
师:他也是分了三步,第一步算出左边这一大部分,第二步算出右边这一部分,第三步合起来。也很好!
师:大家看,23×12,以前我们不会计算,但是咱们大家把它变了变,变成了已学的两位数乘整十数、两位数乘一位数。把没学的变成已经学习的来解决。咱班同学真会思考,其实大家刚才用的方法,就是数学中常说的“转化”。这种方法在以后的学习中,我们会经常用到。
【设计意图:通过给学生创设广阔的思维空间,让学生利用自主创造出来的思路,小组合作探究,找出不同思路下解决问题的方法;很好地培养了学生的思维能力和解决问题的能力,以及小组合作的能力,对后续竖式算理的理解做好了铺垫。】
活动三:尝试列竖式,明确算理和算法。
师:刚才我们是利用口算的方法计算出23×12的结果是276,那还可以怎样做?
生:列竖式。
师:怎样列竖式呢?
大家看,刚才我们借助方格图,分三步求出一共有276个字。那你们能不能用竖式把这三步过程清楚地表示出来呢?
来,试试看。
学生独立完成,教师巡视指导。交流展示。
第一种:
师:说说你的想法。
生:第一步23×2=46,算的是绿色部分;第二步23×10=230,算的是红色部;第三步46+230=276,就是把两部分合起来,求出一共的。
师:他用三个竖式分三步计算出结果,把刚才的过程很好地表示出来了。很好。
第二种:
师:他把三个竖式合在一起了,用一个竖式来表示。谁来说说,他分了几步来完成的?
生1:分三步完成的。
师:是哪三步?
生2:第一步是23×2=46,第二步是23×10=230,第三步是46+230=276。
师:他用一个竖式就计算出了结果,非常好。
第三种:
师:比较一下刚才的方法和这种方法,有没有什么不同?
生:这种方法没写加号,23后面没写0。
师:哦,计算过程是,一样的,只是没写加号和0;我们先来看,23后面不写O,行不行?
生:行。
师:为什么?
生1:因为23乘十位上的1,得到的是23个十,也就是230,所以那个O可以不写。
师:确实,O写上是对的,不写也是对的。
师:O的问题解决了。我们再来看这个加号,可以不写吗?为什么?
生:可以。写上,表示的是把上下两部分合起来;不写,表示的也是把那两个数合起来。
师:哦,写不写表示的含义都是一样的,所以,加号可以写,也可以不写。这种写法,省了0和加号更简单了。
【设计意图:让学生亲身经历由三步横式到竖式,竖式由分别列出的三个竖式,到整合在一起的一个竖式,最后到规范的简化竖式。这里通过这个过程促使学生明白知识间的联系,在理解算理的基础上,深刻感悟出计算中每步简化的优越性;同时让学生学会交流,学会分享,在交流中体验算法多样化,欣赏别人的长处。】
师:看来啊,我们用一个竖式就可以计算出23×12的结果,我们一起来写一下。
先写:23乘l2,要把相同数位对齐。
师:乘的时候,其实就是把l2分成lO和2。通常情况下,我们先乘个位(遮住十位上的1)。
先算23×2,算出两行的。
再算(遮住个位上的2)23乘十位上的1,得23个十,O可以省略不写。2写在百位,3写在十位,一定要把数位对齐。算出这10行的。
然后把这两部分加起来。是276。
师:好了,大家看,开始的时候,我们是用三步,计算出276。(指着竖式。)现在,也是用这三步。虽然书写方式不同,但是道理却一样的。用竖式来计算,更清楚,更便捷了。以后,我们计算两位数乘两位数,就可以用竖式来进行计算。
【设计意图:通过对竖式的规范整理,借助方格图,使数和形有机结合,化抽象为形象,使学生对算理的理解从纯粹的数据分析中走出来,变得有“形”可依。进而,在学生头脑中建立起清晰的三步有序过程,使他们对竖式每一步的理解就不再仅仅是一种计算程序,而是活生生的直观再现。这样学生就充分地体验了由抽象算理到直观算法的过渡和演绎过程,进而达到对算理的深刻理解和对算法的真正掌握。】
活动四:巩固练习。
师:我们做个题目试试,好吗?
1.仿例练习。
师:拿出3号题卡,完成第一题中的两个题目。巡视时,可以提示:有困难的同学,可以像刚才老师那样,把不算的那个数字先遮住。
学生独立完成。
师:多数同学已经完成了,我们一起来看一下。
第1题,第一步算的是:42×2.填84;第二步算的是42×l,表示42个十,也就是420。
那第一步算出的,在图中,就是算出几行的?第二步呢?
师:再看这个012×24,来说一下——第一步算的是?第二步呢?,第三步?你们填对了吗?
大家想一想,如果这里有一个长方形,每行有12个,有这样的24行,第一步算出的几行的?第二步呢?第三步是把4行的和20行的合起来。
师:看来咱们同学已经掌握了两位数乘两位数的方法。再看第二题。
2.火眼金睛辨对错。
师:仔细观察,看看问题出在哪儿?说说吧。
师:第二个43表示的是430,3应该对齐十位。
师:我们在列竖式计算时,需要注意什么啊?一定要把数位对齐。
师:你们记住了?请完成题卡中的“列竖式计算”。
3.竖式计算:23×21。
师:说说怎样想的?第一步算的是23×l,第二步算的是23×20,第三步加起来。
师:看来咱们大家不但会算,还明白了其中的道理。真不错。
活动五:总结反思。
师:一节课马上就要结束了,谁来谈谈你这节课都有哪些收获?
(数学知识方面的:两位数乘两位数的计算,会列竖式计算两位数乘两位数等。)
师:其实我们还有一个收获,那就是在遇到新问题的时候,可以把它转化成已学的知识来解决。有时我们还可以利用图形来帮忙。
师:最后,老师给大家一个建议,课后利用本节课的收获?解决一下三位数乘两位数和三位数乘三位数的问题。相信你们一定能行的。这节课我们就上到这,下课。
1 / 8
