2021-2022学年人教版数学八年级下册第18章平行四边形测试题(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册第18章平行四边形测试题(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 713.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 14:28:20 | ||
图片预览



文档简介
2021-2022学年度初中数学八年级下册第十八章
平行四边形试题
一、单选题
1.如图,将矩形纸片ABCD沿EF折叠,使点A恰好与点C重合,点B的对应点为点B′,若DC=4,AF=5,则BC的长为( )
A. B. C.10 D.8
2.下列条件中,不能判定平行四边形ABCD为矩形的是( )
A.∠A=∠C B.∠A=∠B C.AC=BD D.AB⊥BC
3.已知:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE至点F,使得EF=DE,那么四边形AFCD一定是( )
A.菱形 B.矩形 C.直角梯形 D.等腰梯形
4.如图,在中,,于点D,F在BC上且,连接AF,E为AF的中点,连接DE,则DE的长为( )
A.1 B.2 C.3 D.4
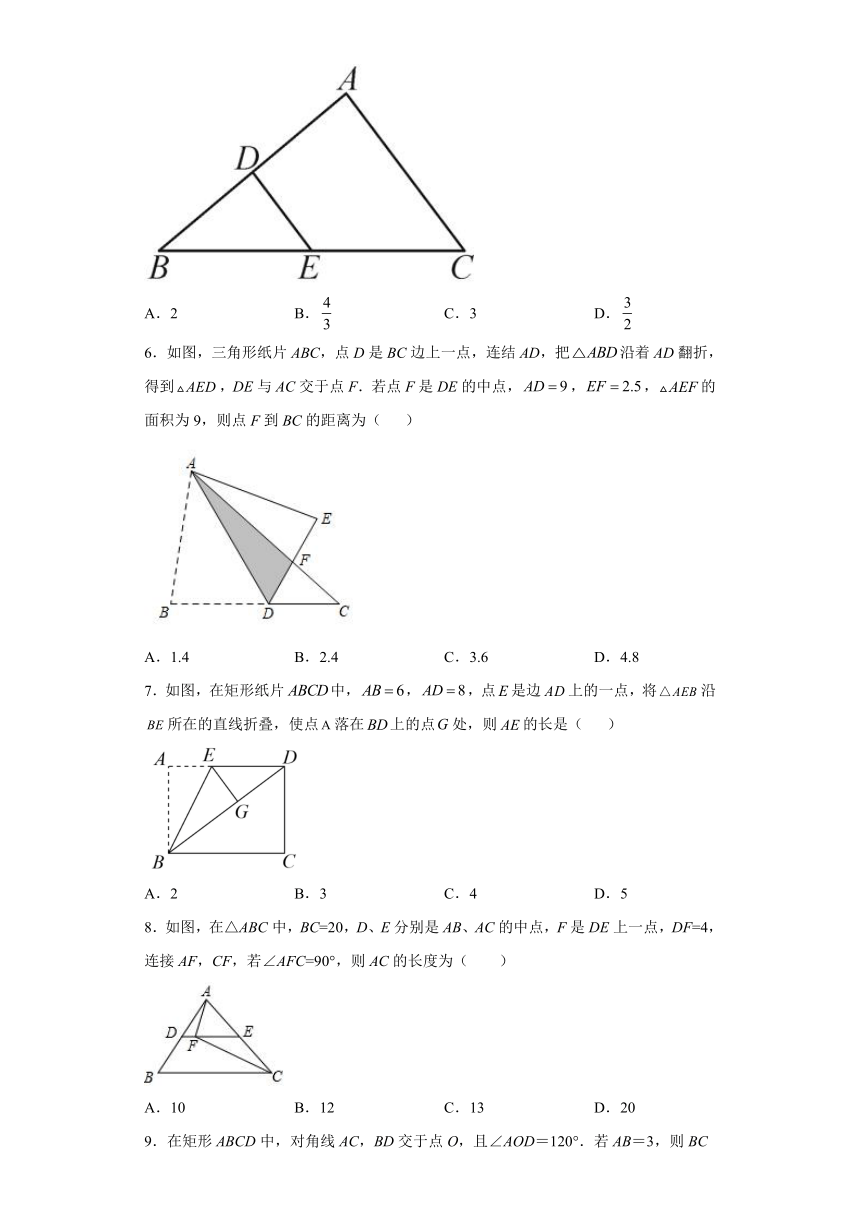
5.如图,点D,E分别是△ABC边BA,BC的中点,AC=3,则DE的长为( )
A.2 B. C.3 D.
6.如图,三角形纸片ABC,点D是BC边上一点,连结AD,把沿着AD翻折,得到,DE与AC交于点F.若点F是DE的中点,,,的面积为9,则点F到BC的距离为( )
A.1.4 B.2.4 C.3.6 D.4.8
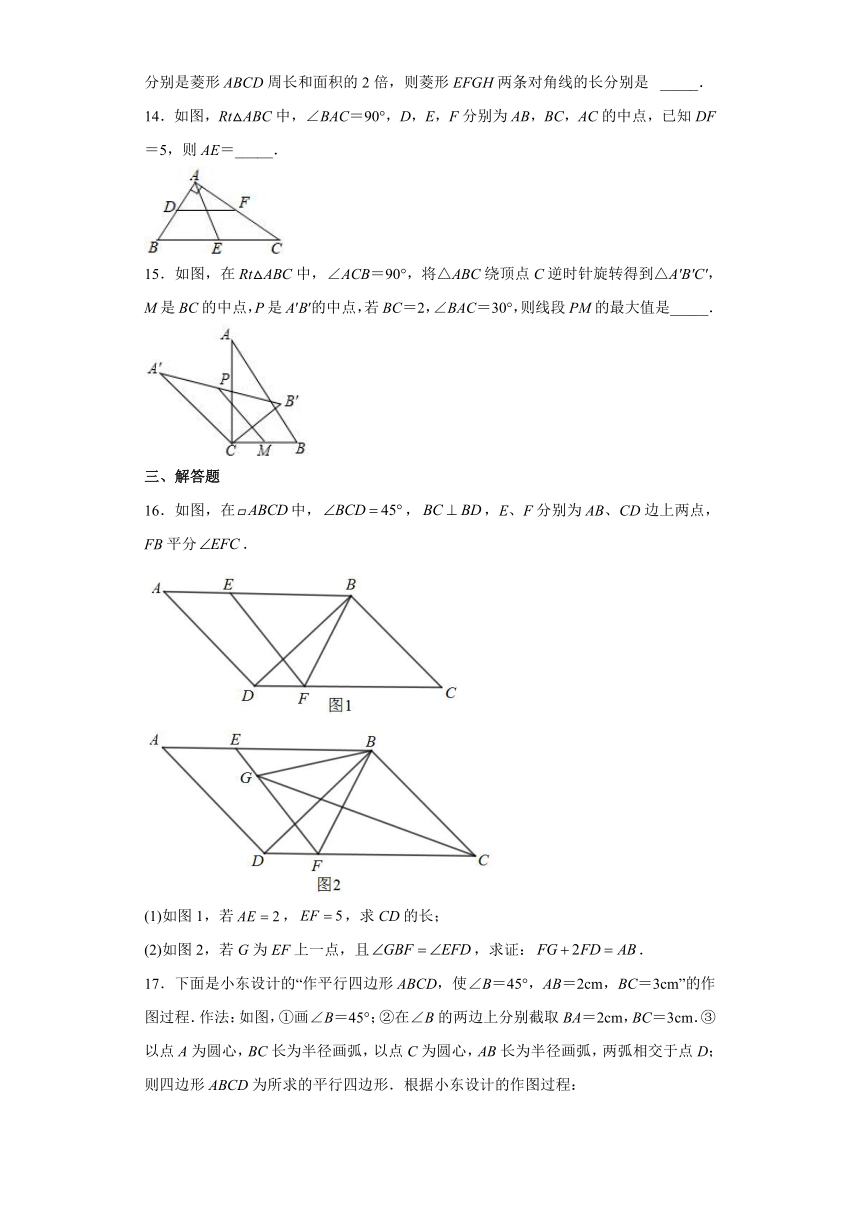
7.如图,在矩形纸片中,,,点是边上的一点,将沿所在的直线折叠,使点落在上的点处,则的长是( )
A.2 B.3 C.4 D.5
8.如图,在△ABC中,BC=20,D、E分别是AB、AC的中点,F是DE上一点,DF=4,连接AF,CF,若∠AFC=90°,则AC的长度为( )
A.10 B.12 C.13 D.20
9.在矩形ABCD中,对角线AC,BD交于点O,且∠AOD=120°.若AB=3,则BC的长为( )
A. B.3 C. D.6
10.如图,等腰中,,于,的平分线分别交、于点、,的平分线分别交、于点、,连接、,下列结论:①;②;③是等边三角形;④;⑤垂直平分,其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.如图,在中,分别为的中点.若,则的长度为_______.
12.如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将ADF绕点A顺时针旋转90°得到ABG,若BE=2,则EF的长为___.
13.已知菱形ABCD两条对角线的长分别为6和8,若另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,则菱形EFGH两条对角线的长分别是 _____.
14.如图,Rt△ABC中,∠BAC=90°,D,E,F分别为AB,BC,AC的中点,已知DF=5,则AE=_____.
15.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C′,M是BC的中点,P是A′B′的中点,若BC=2,∠BAC=30°,则线段PM的最大值是_____.
三、解答题
16.如图,在中,,,E、F分别为AB、CD边上两点,FB平分.
(1)如图1,若,,求CD的长;
(2)如图2,若G为EF上一点,且,求证:.
17.下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.作法:如图,①画∠B=45°;②在∠B的两边上分别截取BA=2cm,BC=3cm.③以点A为圆心,BC长为半径画弧,以点C为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.根据小东设计的作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB= ,CB= ,
∴四边形ABCD为所求的平行四边形( )(填推理的依据).
18.(1)【发现证明】
如图1,在正方形中,点,分别是,边上的动点,且,求证:.小明发现,当把绕点顺时针旋转90°至,使与重合时能够证明,请你给出证明过程.
(2)【类比引申】
①如图2,在正方形中,如果点,分别是,延长线上的动点,且,则(1)中的结论还成立吗?若不成立,请写出,,之间的数量关系______(不要求证明)
②如图3,如果点,分别是,延长线上的动点,且,则,,之间的数量关系是______(不要求证明)
(3)【联想拓展】如图1,若正方形的边长为6,,求的长.
19.如图,在中,于点E,延长BC至点F,使,连接AF,DE,DF.
(1)求证:四边形AEFD为矩形;
(2)若,,,求DF的长.
试卷第1页,共3页
参考答案:
1.D
【详解】
解:由折叠得:FA=FC=5,
∵四边形ABCD是矩形,CD=4,
∴△CDF是直角三角形,
∴DF==3,
∴BC=AD=AF+DF=8;
故选:D.
2.A
【详解】
解:A、在 ABCD,若∠A=∠C,
则四边形ABCD还是平行四边形;故选项A符合题意;
B、在 ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD是矩形,故选项B不符合题意;
C、在 ABCD中,AC=BD,
则 ABCD是矩形;故选项C不符合题意;
D、在 ABCD中,AB⊥BC,
∴∠ABC=90°,
∴ ABCD是矩形,故选项D不符合题意;
故选:A.
3.B
【详解】
解:∵E是AC中点,
∴AE=EC,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵AD=DB,AE=EC,
∴DE=BC,
∴DF=BC,
∵CA=CB,
∴AC=DF,
∴四边形ADCF是矩形;
故选:B.
4.B
【详解】
解:,
,
,
(等腰三角形的三线合一),
即点是的中点,
为的中点,
是的中位线,
,
故选:B.
5.D
【解析】
略
6.B
【详解】
如图,连接BE,交AD于点O.过点E作于点H,点F作于点G,
由翻折可知AB=AE,,BD=DE,
又∵AO=AO,
∴,
∴BO=EO,,
∴.
∵点F是DE的中点,EF=2.5,
∴DF=EF=2.5,BD=DE=5,
∴和等底同高,
∴.
∵,
∴,
解得:.
∴在中,,
∵.
∴.
又∵,
∴,
解得:.
∵点F是DE的中点,,,
∴FG为中位线,
∴.
故选B.
7.B
【详解】
解:根据题意得: ,
在矩形纸片中, ,
∴ ,
∴ ,
设 ,则 ,
在 中, ,
∴ ,解得: ,
即 .
故选:B
8.B
【详解】
解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=10,
∴EF=DE-DF=10-4=6,
在Rt△AFC中,AE=EC,
∴AC=2EF=12,
故选:B.
9.C
【详解】
解:∵∠AOD=120°,∠AOD+∠AOB=180°,
∴∠AOB=60°,
∵四边形ABCD是矩形,
∴OA=OB=OC,∠ABC=90°,
∴△AOB是等边三角形,
∴AB=OA=OC,
∵AB=3,
∴AC=6,
∴BC= ,
故选:C.
10.C
【详解】
解:,,,
,,,,
平分,
,
,
,
,
为的中点,
,
,
,
在和中
,
,
,故①正确;
∵AN平分∠CAD,
∴,
在和中
,
,
,
,
,故②正确;
,为的中点,
,
,
同理,
,
平分,
,
,
,
,
,
,
垂直平分,故⑤正确;
,
,
,
,
,
是等腰三角形,
而,
不是等边三角形,故③错误,
,,
,
,
,
,
,故④正确;
即正确的有4个,
故选:.
11.4
【详解】
解:∵分别为的中点.
∴ ,
∵为的中点.
∴ ,
∵,
∴ ,
∴ 是等边三角形,
∴.
故答案为:4
12.5
【详解】
解:由旋转的性质可知:,,,
,
点在的延长线上,
四边形为正方形,
.
又,
.
.
.
在和中,
,
,
,
,
,
,
,
,
故答案为:5.
13.,
【详解】
解:如图,菱形ABCD中,AC=8,BD=6,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB==5,
∴菱形ABCD的周长是:5×4=20,面积是:×6×8=24.
∵另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,
∴菱形EFGH的周长和面积分别是40,48,
∴菱形EFGH的边长是10,
设菱形EFGH的对角线为2a,2b,
∴a2+b2=100,×2a×2b=48,
∴a=,b=,
∴菱形EFGH两条对角线的长分别是,,
故答案为:2,.
14.5
【详解】
∵ D,F分别为AB,AC的中点,
∴DF是△ABC的中位线,
∴BC=2DF=10,
在Rt△ABC中,E为BC的中点,
故答案为:5.
15.3
【详解】
解:连结PC,
∵∠ACB=90°,BC=2,∠BAC=30°,
∴AB=2BC=4,
∵将△ABC绕顶点C逆时针旋转得到△A′B′C′,
∴=AB=4,
∵M为BC中点,
∴CM=,
∵点P为的中点,△是直角三角形,
∴CP=,
根据两点间距离得出PM≤PC+CM,
当点P、C、M三点共线时PM最大,PM最大=PC+CM=2+1=3.
故答案为:3.
16.(1)7
(2)见解析
(1)
解:在中,AB∥CD,AB=CD,
∴∠EBF=∠CFB,
∵FB平分,
∴∠EFB=∠CFB,
∴∠EFB=∠EBF,
∴BE=EF=5,
∵AE=2,
∴CD=AB=AE+BE=7;
(2)
证明:如图,再CF上截取FN=FG,
∵,
∴ ,
∴∠BGF=∠BNF,
∵ ,∠BFG+∠BGF+∠GBF=180°,∠GBF=∠EFD,
∴∠BGF=∠BFN,
∴∠BFN=∠BNF,
∴∠BFD=∠BNC,
∵BC⊥BD,
∴∠CBD=90°,
∵∠BCD=45°,
∴∠BDC=∠BCD=45°,
∴BC=BD,
∴△BDF≌△BCN(AAS),
∴NC=FD,
∴CD=DF+FN+CN=2FD+FG,
∵AB=CD,
∴FG+2FD=AB.
17.(1)见解析
(2)CD;AD;两组对边分别相等的四边形是平行四边形
(1)
补全图形如下,
.
(2)
∵AB=CD,CB=AD
∴四边形ABCD为所求的平行四边形(两组对边分别相等的四边形是平行四边形).
故答案为:CD,AD,两组对边分别相等的四边形是平行四边形.
18.(1)见解析;(2)①不成立,结论:;②,见解析;(3)
【详解】
(1)证明:把绕点顺时针旋转至,如图1,
,,,
,
,,三点共线,
,
,
,
,
,
,
,
;
(2)①不成立,结论:;
证明:如图2,将绕点顺时针旋转至,
,,,,
,
,
,
;
②如图3,将绕点逆时针旋转至,
,,
,
,
,
,
,
,
.
即.
故答案为:.
(3)解:由(1)可知,
正方形的边长为6,
,
.
,
,
设,则,,
在中,
,
,
解得:.
,
.
19.(1)见解析
(2)
(1)
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
∵ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD为矩形.
(2)
∵四边形AEFD为矩形,
∴AF=DE=4,DF=AE,
∵,,,
∴AB2+AF2=BF2,
∴△BAF为直角三角形,∠BAF=90°,
∴,
∴AE=,
∴.
答案第1页,共2页
答案第14页,共15页
平行四边形试题
一、单选题
1.如图,将矩形纸片ABCD沿EF折叠,使点A恰好与点C重合,点B的对应点为点B′,若DC=4,AF=5,则BC的长为( )
A. B. C.10 D.8
2.下列条件中,不能判定平行四边形ABCD为矩形的是( )
A.∠A=∠C B.∠A=∠B C.AC=BD D.AB⊥BC
3.已知:在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,延长DE至点F,使得EF=DE,那么四边形AFCD一定是( )
A.菱形 B.矩形 C.直角梯形 D.等腰梯形
4.如图,在中,,于点D,F在BC上且,连接AF,E为AF的中点,连接DE,则DE的长为( )
A.1 B.2 C.3 D.4
5.如图,点D,E分别是△ABC边BA,BC的中点,AC=3,则DE的长为( )
A.2 B. C.3 D.
6.如图,三角形纸片ABC,点D是BC边上一点,连结AD,把沿着AD翻折,得到,DE与AC交于点F.若点F是DE的中点,,,的面积为9,则点F到BC的距离为( )
A.1.4 B.2.4 C.3.6 D.4.8
7.如图,在矩形纸片中,,,点是边上的一点,将沿所在的直线折叠,使点落在上的点处,则的长是( )
A.2 B.3 C.4 D.5
8.如图,在△ABC中,BC=20,D、E分别是AB、AC的中点,F是DE上一点,DF=4,连接AF,CF,若∠AFC=90°,则AC的长度为( )
A.10 B.12 C.13 D.20
9.在矩形ABCD中,对角线AC,BD交于点O,且∠AOD=120°.若AB=3,则BC的长为( )
A. B.3 C. D.6
10.如图,等腰中,,于,的平分线分别交、于点、,的平分线分别交、于点、,连接、,下列结论:①;②;③是等边三角形;④;⑤垂直平分,其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.如图,在中,分别为的中点.若,则的长度为_______.
12.如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将ADF绕点A顺时针旋转90°得到ABG,若BE=2,则EF的长为___.
13.已知菱形ABCD两条对角线的长分别为6和8,若另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,则菱形EFGH两条对角线的长分别是 _____.
14.如图,Rt△ABC中,∠BAC=90°,D,E,F分别为AB,BC,AC的中点,已知DF=5,则AE=_____.
15.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C′,M是BC的中点,P是A′B′的中点,若BC=2,∠BAC=30°,则线段PM的最大值是_____.
三、解答题
16.如图,在中,,,E、F分别为AB、CD边上两点,FB平分.
(1)如图1,若,,求CD的长;
(2)如图2,若G为EF上一点,且,求证:.
17.下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.作法:如图,①画∠B=45°;②在∠B的两边上分别截取BA=2cm,BC=3cm.③以点A为圆心,BC长为半径画弧,以点C为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.根据小东设计的作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB= ,CB= ,
∴四边形ABCD为所求的平行四边形( )(填推理的依据).
18.(1)【发现证明】
如图1,在正方形中,点,分别是,边上的动点,且,求证:.小明发现,当把绕点顺时针旋转90°至,使与重合时能够证明,请你给出证明过程.
(2)【类比引申】
①如图2,在正方形中,如果点,分别是,延长线上的动点,且,则(1)中的结论还成立吗?若不成立,请写出,,之间的数量关系______(不要求证明)
②如图3,如果点,分别是,延长线上的动点,且,则,,之间的数量关系是______(不要求证明)
(3)【联想拓展】如图1,若正方形的边长为6,,求的长.
19.如图,在中,于点E,延长BC至点F,使,连接AF,DE,DF.
(1)求证:四边形AEFD为矩形;
(2)若,,,求DF的长.
试卷第1页,共3页
参考答案:
1.D
【详解】
解:由折叠得:FA=FC=5,
∵四边形ABCD是矩形,CD=4,
∴△CDF是直角三角形,
∴DF==3,
∴BC=AD=AF+DF=8;
故选:D.
2.A
【详解】
解:A、在 ABCD,若∠A=∠C,
则四边形ABCD还是平行四边形;故选项A符合题意;
B、在 ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴ ABCD是矩形,故选项B不符合题意;
C、在 ABCD中,AC=BD,
则 ABCD是矩形;故选项C不符合题意;
D、在 ABCD中,AB⊥BC,
∴∠ABC=90°,
∴ ABCD是矩形,故选项D不符合题意;
故选:A.
3.B
【详解】
解:∵E是AC中点,
∴AE=EC,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵AD=DB,AE=EC,
∴DE=BC,
∴DF=BC,
∵CA=CB,
∴AC=DF,
∴四边形ADCF是矩形;
故选:B.
4.B
【详解】
解:,
,
,
(等腰三角形的三线合一),
即点是的中点,
为的中点,
是的中位线,
,
故选:B.
5.D
【解析】
略
6.B
【详解】
如图,连接BE,交AD于点O.过点E作于点H,点F作于点G,
由翻折可知AB=AE,,BD=DE,
又∵AO=AO,
∴,
∴BO=EO,,
∴.
∵点F是DE的中点,EF=2.5,
∴DF=EF=2.5,BD=DE=5,
∴和等底同高,
∴.
∵,
∴,
解得:.
∴在中,,
∵.
∴.
又∵,
∴,
解得:.
∵点F是DE的中点,,,
∴FG为中位线,
∴.
故选B.
7.B
【详解】
解:根据题意得: ,
在矩形纸片中, ,
∴ ,
∴ ,
设 ,则 ,
在 中, ,
∴ ,解得: ,
即 .
故选:B
8.B
【详解】
解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=BC=10,
∴EF=DE-DF=10-4=6,
在Rt△AFC中,AE=EC,
∴AC=2EF=12,
故选:B.
9.C
【详解】
解:∵∠AOD=120°,∠AOD+∠AOB=180°,
∴∠AOB=60°,
∵四边形ABCD是矩形,
∴OA=OB=OC,∠ABC=90°,
∴△AOB是等边三角形,
∴AB=OA=OC,
∵AB=3,
∴AC=6,
∴BC= ,
故选:C.
10.C
【详解】
解:,,,
,,,,
平分,
,
,
,
,
为的中点,
,
,
,
在和中
,
,
,故①正确;
∵AN平分∠CAD,
∴,
在和中
,
,
,
,
,故②正确;
,为的中点,
,
,
同理,
,
平分,
,
,
,
,
,
,
垂直平分,故⑤正确;
,
,
,
,
,
是等腰三角形,
而,
不是等边三角形,故③错误,
,,
,
,
,
,
,故④正确;
即正确的有4个,
故选:.
11.4
【详解】
解:∵分别为的中点.
∴ ,
∵为的中点.
∴ ,
∵,
∴ ,
∴ 是等边三角形,
∴.
故答案为:4
12.5
【详解】
解:由旋转的性质可知:,,,
,
点在的延长线上,
四边形为正方形,
.
又,
.
.
.
在和中,
,
,
,
,
,
,
,
,
故答案为:5.
13.,
【详解】
解:如图,菱形ABCD中,AC=8,BD=6,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB==5,
∴菱形ABCD的周长是:5×4=20,面积是:×6×8=24.
∵另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,
∴菱形EFGH的周长和面积分别是40,48,
∴菱形EFGH的边长是10,
设菱形EFGH的对角线为2a,2b,
∴a2+b2=100,×2a×2b=48,
∴a=,b=,
∴菱形EFGH两条对角线的长分别是,,
故答案为:2,.
14.5
【详解】
∵ D,F分别为AB,AC的中点,
∴DF是△ABC的中位线,
∴BC=2DF=10,
在Rt△ABC中,E为BC的中点,
故答案为:5.
15.3
【详解】
解:连结PC,
∵∠ACB=90°,BC=2,∠BAC=30°,
∴AB=2BC=4,
∵将△ABC绕顶点C逆时针旋转得到△A′B′C′,
∴=AB=4,
∵M为BC中点,
∴CM=,
∵点P为的中点,△是直角三角形,
∴CP=,
根据两点间距离得出PM≤PC+CM,
当点P、C、M三点共线时PM最大,PM最大=PC+CM=2+1=3.
故答案为:3.
16.(1)7
(2)见解析
(1)
解:在中,AB∥CD,AB=CD,
∴∠EBF=∠CFB,
∵FB平分,
∴∠EFB=∠CFB,
∴∠EFB=∠EBF,
∴BE=EF=5,
∵AE=2,
∴CD=AB=AE+BE=7;
(2)
证明:如图,再CF上截取FN=FG,
∵,
∴ ,
∴∠BGF=∠BNF,
∵ ,∠BFG+∠BGF+∠GBF=180°,∠GBF=∠EFD,
∴∠BGF=∠BFN,
∴∠BFN=∠BNF,
∴∠BFD=∠BNC,
∵BC⊥BD,
∴∠CBD=90°,
∵∠BCD=45°,
∴∠BDC=∠BCD=45°,
∴BC=BD,
∴△BDF≌△BCN(AAS),
∴NC=FD,
∴CD=DF+FN+CN=2FD+FG,
∵AB=CD,
∴FG+2FD=AB.
17.(1)见解析
(2)CD;AD;两组对边分别相等的四边形是平行四边形
(1)
补全图形如下,
.
(2)
∵AB=CD,CB=AD
∴四边形ABCD为所求的平行四边形(两组对边分别相等的四边形是平行四边形).
故答案为:CD,AD,两组对边分别相等的四边形是平行四边形.
18.(1)见解析;(2)①不成立,结论:;②,见解析;(3)
【详解】
(1)证明:把绕点顺时针旋转至,如图1,
,,,
,
,,三点共线,
,
,
,
,
,
,
,
;
(2)①不成立,结论:;
证明:如图2,将绕点顺时针旋转至,
,,,,
,
,
,
;
②如图3,将绕点逆时针旋转至,
,,
,
,
,
,
,
,
.
即.
故答案为:.
(3)解:由(1)可知,
正方形的边长为6,
,
.
,
,
设,则,,
在中,
,
,
解得:.
,
.
19.(1)见解析
(2)
(1)
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
∵ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD为矩形.
(2)
∵四边形AEFD为矩形,
∴AF=DE=4,DF=AE,
∵,,,
∴AB2+AF2=BF2,
∴△BAF为直角三角形,∠BAF=90°,
∴,
∴AE=,
∴.
答案第1页,共2页
答案第14页,共15页
