通用技术-第一章第三节结构的强度与稳定性(第一课时)(52张幻灯片)
文档属性
| 名称 | 通用技术-第一章第三节结构的强度与稳定性(第一课时)(52张幻灯片) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 通用技术 | ||
| 更新时间 | 2012-12-16 14:29:20 | ||
图片预览











文档简介
课件52张PPT。第三节 结构的强度与稳定性(一)淄博中学 有何感想?有何感想?有何感想?有何感想?一、“结实”和“稳”课本技术实验
试验1 简易拉伸试验
试验2 简易弯曲试验
试验3 简易组态试验试验1 简易拉伸试验结论:
多股绳比单股绳抗变形能力 ,即:粗绳抗拉强度
大大试验2 简易弯曲试验结论: 厚梁比薄梁的截面积 ,抗弯强度 。大大试验3 简易组态试验
PP结论?三角形比四边形稳定技术试验后的回顾与思考 前面的技术试验,让我们思考了哪些问题呢?自学课本p24应力与强度内力是什么?
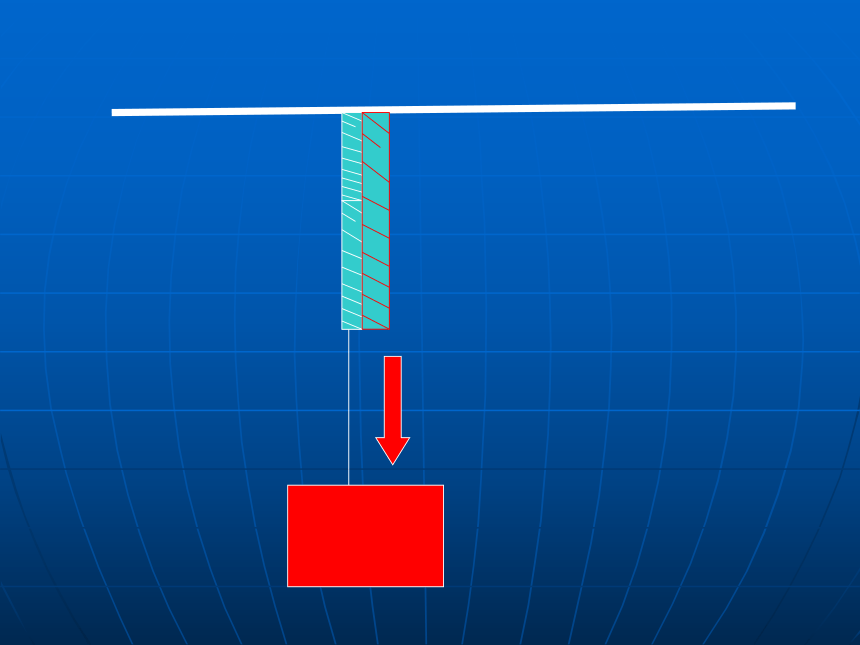
外力使构件发生变形的同时,构件内部分子之间随之产生一种抵抗变形的抵抗力,称为内力 。
内力,就是用来抵抗外力与变形,并力图使变形部分复原的力。内力内力内力如何抵抗外力图示1内力如何抵抗外力图示2内力内力内力如何抵抗外力图示3弯曲力内力应力是什么?如何计算?单位?
应力:作用在单位面积上的内力。
δ=
容许应力是什么?
材料能承受的应力有一个最大值,称为容许应力。对应最大内力。
当外力大于内力的最大值,或者结构受到的应力大于容许应力时,结构就会被破坏。何为强度?如何表述?
物体抵抗变形的能力称为强度。
结构的最大内力越大,要破坏它所需的外力也就越大,也可以说,它的强度越大。
强度可以通过应力来衡量。同一截面积,容许应力越大,强度也就越 ;容许应力越小,强度也就越 。大小容许应力和应力的差别?通用技术·技术与设计二第三节 结构的强度与稳定性 【结构的强度】①图中的花杆支柱,最薄弱的地方是______处,
原因是__________________________________________。B此处截面积最小,材料承受应力最大学以致用: 阅读课本 P26材料,回答 下列问题:②如果置于上板面的荷载超过杆件的承受能力,杆件会发生变形为________。断裂 影响结构强度的因素 ——形状1.构成的形状略有改变,强度就会改变。
不同形状的结构有着不同的强度。结构的形状对强度的影响主要是
一是结构的外部形状。
二是结构的构件截面积形状。
构件的截面积形状各种各样,有工字形、十字形、长方形、L形、圆形、U形、扭转形等。不同横截面形状的构件所能承受力的程度是不一样的。 影响结构强度的因素 ——形状“工”字形横梁
被广泛应用通用技术·技术与设计二第三节 结构的强度与稳定性 【结构的强度】③同形状,同尺寸的花展架,为什么铁质的 比木质的更能承载?答:因为铁质的容许应力比木质的容许应力大。学以致用: 阅读课本 P26材料,回答 下列问题: 影响结构强度的因素 ——材料2.形状相同,材料不同,强度就不同。
任何构件在设计和使用过程中都要考虑构成材料的各种属性。?
通用技术·技术与设计二第三节 结构的强度与稳定性 【结构的强度】探究试验:☆ 实验一:简易纸板弯曲试验记录表☆ 瓦楞状结构比平板状结构承受能力强弯曲得厉害看不到弯曲依然无明显弯曲 不同的连接方式,受力传递方式和效果不一样。 影响结构强度的因素 ——材料的连接方式阅读材料p27“连接方式多种多样”从实现连接的形态来看连接方式有哪些?
从连接件的状态来看连接方式有哪些?
铰连接——被连接的构件在连接处不能相对
移动,但能相对转动。 刚连接——被连接的构件在连接处既不能相对移动,也不能相对转动,具体有榫接、胶接、焊接等。(1).对一个用4根小木条钉成的相片框,使它更牢固的做法是什么?马上行动可用直角铁片固定在连接处的背面。(2).比较左图中同一结构的几种连接方式,请预言哪种连接方式的强度更好。 左边的榫卯连接的强度最大,上下、左右、前后各方向都被牢牢固定住,所以强度最大。中间的连接方式强度最小,钉子是从侧面钉进去的,中间的横梁不能承受较重物体的压力,所以强度最小。14、下列自行车四个部位的连接中属于铰连接的是B10、下列常用工具中属于刚连接的是D一根筷子和一把筷子的故事古代有几兄弟经常打架,父亲就给他们现身说法:一根筷子容易被人折断,两根筷子还是容易折断,三根筷子有点难……十根筷子就折不断了。从此,几兄弟便团结起来。
试解释,为何一根筷子容易断,多根筷子不易断?
答:一根筷子的截面积小,所受应力就大;多根筷子一起,截面积变大了,所受应力就小了
已知结构的容许应力为50 N/cm2,截面积为4 cm2,外力冲击产生的内力为180N,请问结构会被破坏吗?(解法1) 180/4=45 N/cm2,小于容许应力,所以不会被破坏
(解法2) 4*50N/cm2=200N,外力小于内力的最大值,所以不会被破坏。 如何判断外力能否破坏结构?
1、假设内力等于外力,计算出应力,与容许应力比较,如果大于容许应力,结构会被破坏。
2、由容许应力计算出最大内力,如果外力比最大内力还要大,则结构会被破坏。
P26 试一试假设花杆支柱最粗处的直径为3cm,最细处的直径为最粗处的一半,外力冲击所产生的内力为30N,试计算支柱上的最大应力为多少? 解:最细处的截面积最小,所受的应力最大,最容易被破坏,是整个支柱最薄弱的地方,所以支柱所能承受的最大应力取决于最细处的应力。
δ=30/(3.14*0.75*0.75)=16.98 N/cm2谢谢合作 !
试验1 简易拉伸试验
试验2 简易弯曲试验
试验3 简易组态试验试验1 简易拉伸试验结论:
多股绳比单股绳抗变形能力 ,即:粗绳抗拉强度
大大试验2 简易弯曲试验结论: 厚梁比薄梁的截面积 ,抗弯强度 。大大试验3 简易组态试验
PP结论?三角形比四边形稳定技术试验后的回顾与思考 前面的技术试验,让我们思考了哪些问题呢?自学课本p24应力与强度内力是什么?
外力使构件发生变形的同时,构件内部分子之间随之产生一种抵抗变形的抵抗力,称为内力 。
内力,就是用来抵抗外力与变形,并力图使变形部分复原的力。内力内力内力如何抵抗外力图示1内力如何抵抗外力图示2内力内力内力如何抵抗外力图示3弯曲力内力应力是什么?如何计算?单位?
应力:作用在单位面积上的内力。
δ=
容许应力是什么?
材料能承受的应力有一个最大值,称为容许应力。对应最大内力。
当外力大于内力的最大值,或者结构受到的应力大于容许应力时,结构就会被破坏。何为强度?如何表述?
物体抵抗变形的能力称为强度。
结构的最大内力越大,要破坏它所需的外力也就越大,也可以说,它的强度越大。
强度可以通过应力来衡量。同一截面积,容许应力越大,强度也就越 ;容许应力越小,强度也就越 。大小容许应力和应力的差别?通用技术·技术与设计二第三节 结构的强度与稳定性 【结构的强度】①图中的花杆支柱,最薄弱的地方是______处,
原因是__________________________________________。B此处截面积最小,材料承受应力最大学以致用: 阅读课本 P26材料,回答 下列问题:②如果置于上板面的荷载超过杆件的承受能力,杆件会发生变形为________。断裂 影响结构强度的因素 ——形状1.构成的形状略有改变,强度就会改变。
不同形状的结构有着不同的强度。结构的形状对强度的影响主要是
一是结构的外部形状。
二是结构的构件截面积形状。
构件的截面积形状各种各样,有工字形、十字形、长方形、L形、圆形、U形、扭转形等。不同横截面形状的构件所能承受力的程度是不一样的。 影响结构强度的因素 ——形状“工”字形横梁
被广泛应用通用技术·技术与设计二第三节 结构的强度与稳定性 【结构的强度】③同形状,同尺寸的花展架,为什么铁质的 比木质的更能承载?答:因为铁质的容许应力比木质的容许应力大。学以致用: 阅读课本 P26材料,回答 下列问题: 影响结构强度的因素 ——材料2.形状相同,材料不同,强度就不同。
任何构件在设计和使用过程中都要考虑构成材料的各种属性。?
通用技术·技术与设计二第三节 结构的强度与稳定性 【结构的强度】探究试验:☆ 实验一:简易纸板弯曲试验记录表☆ 瓦楞状结构比平板状结构承受能力强弯曲得厉害看不到弯曲依然无明显弯曲 不同的连接方式,受力传递方式和效果不一样。 影响结构强度的因素 ——材料的连接方式阅读材料p27“连接方式多种多样”从实现连接的形态来看连接方式有哪些?
从连接件的状态来看连接方式有哪些?
铰连接——被连接的构件在连接处不能相对
移动,但能相对转动。 刚连接——被连接的构件在连接处既不能相对移动,也不能相对转动,具体有榫接、胶接、焊接等。(1).对一个用4根小木条钉成的相片框,使它更牢固的做法是什么?马上行动可用直角铁片固定在连接处的背面。(2).比较左图中同一结构的几种连接方式,请预言哪种连接方式的强度更好。 左边的榫卯连接的强度最大,上下、左右、前后各方向都被牢牢固定住,所以强度最大。中间的连接方式强度最小,钉子是从侧面钉进去的,中间的横梁不能承受较重物体的压力,所以强度最小。14、下列自行车四个部位的连接中属于铰连接的是B10、下列常用工具中属于刚连接的是D一根筷子和一把筷子的故事古代有几兄弟经常打架,父亲就给他们现身说法:一根筷子容易被人折断,两根筷子还是容易折断,三根筷子有点难……十根筷子就折不断了。从此,几兄弟便团结起来。
试解释,为何一根筷子容易断,多根筷子不易断?
答:一根筷子的截面积小,所受应力就大;多根筷子一起,截面积变大了,所受应力就小了
已知结构的容许应力为50 N/cm2,截面积为4 cm2,外力冲击产生的内力为180N,请问结构会被破坏吗?(解法1) 180/4=45 N/cm2,小于容许应力,所以不会被破坏
(解法2) 4*50N/cm2=200N,外力小于内力的最大值,所以不会被破坏。 如何判断外力能否破坏结构?
1、假设内力等于外力,计算出应力,与容许应力比较,如果大于容许应力,结构会被破坏。
2、由容许应力计算出最大内力,如果外力比最大内力还要大,则结构会被破坏。
P26 试一试假设花杆支柱最粗处的直径为3cm,最细处的直径为最粗处的一半,外力冲击所产生的内力为30N,试计算支柱上的最大应力为多少? 解:最细处的截面积最小,所受的应力最大,最容易被破坏,是整个支柱最薄弱的地方,所以支柱所能承受的最大应力取决于最细处的应力。
δ=30/(3.14*0.75*0.75)=16.98 N/cm2谢谢合作 !
同课章节目录
