第18章平行四边形练习题2020-2021年山东省部分地区人教版数学八年级下学期期末试题选编(Word版含解析)
文档属性
| 名称 | 第18章平行四边形练习题2020-2021年山东省部分地区人教版数学八年级下学期期末试题选编(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览




文档简介
第18章:平行四边形练习题
一、单选题
1.(2021·山东鄄城·八年级期末)如图, ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A.15 B.18 C.21 D.24
2.(2021·山东莱阳·八年级期末)小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,② B.①,④ C.③,④ D.②,③
3.(2021·山东·东平县实验中学八年级期末)已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE=DC B.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
4.(2021·山东冠县·八年级期末)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
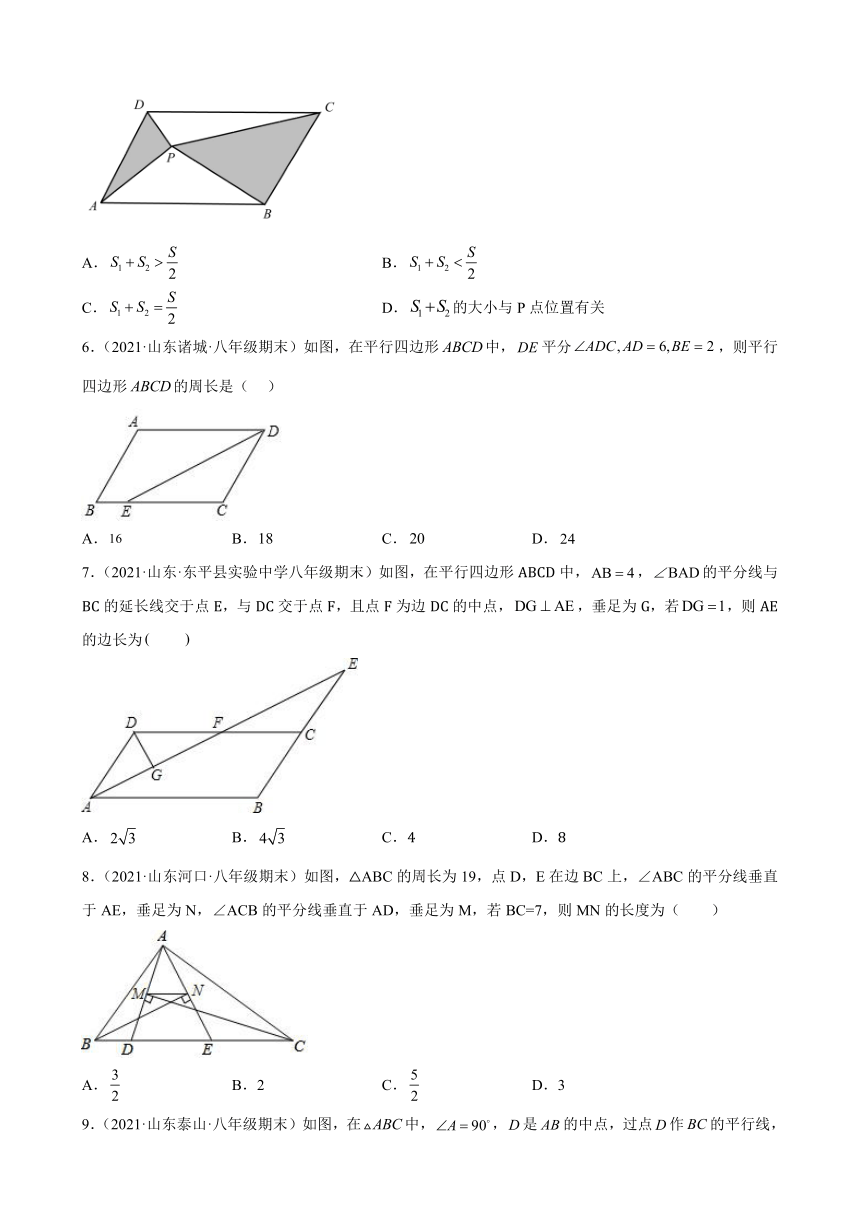
5.(2021·山东蒙阴·八年级期末)如图,P是面积为S的内任意一点,的面积为,的面积为,则( )
A. B.
C. D.的大小与P点位置有关
6.(2021·山东诸城·八年级期末)如图,在平行四边形中,平分,则平行四边形的周长是( )
A. B. C. D.
7.(2021·山东·东平县实验中学八年级期末)如图,在平行四边形ABCD中,,的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,,垂足为G,若,则AE的边长为
A. B. C.4 D.8
8.(2021·山东河口·八年级期末)如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
A. B.2 C. D.3
9.(2021·山东泰山·八年级期末)如图,在中,,是的中点,过点作的平行线,交于点E,作的垂线交于点,若,且的面积为1,则的长为( )
A. B.5 C. D.10
10.(2021·山东台儿庄·八年级期末)已知的周长为16,点,,分别为三条边的中点,则的周长为( )
A.8 B. C.16 D.4
11.(2021·山东莒南·八年级期末)如图,是边延长线上一点,连接,,,交于点.添加以下条件,不能判定四边形为平行四边形的是( )
A. B.
C. D.
12.(2021·山东郓城·八年级期末)如图,在四边形中,是边的中点,连接并延长,交的延长线于点,.添加一个条件使四边形是平行四边形,你认为下面四个条件中可选择的是( )
A. B. C. D.
13.(2021·山东台儿庄·八年级期末)如图,在四边形ABCD中,AC与BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AB=DC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
14.(2021·山东莱阳·八年级期末)如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
15.(2021·山东河口·八年级期末)如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=5.正确的个数是( )
A.1个 B.2个
C.3个 D.4个
16.(2021·山东·夏津县教学工作研究室八年级期末)如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4
C.5 D.6
17.(2021·山东蒙阴·八年级期末)如图,将矩形折叠,使点和点重合,折痕为,与交于点若,,则的长为( )
A. B. C. D.
18.(2021·山东兖州·八年级期末)如图,将一个边长为4和8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
A. B. C. D.
19.(2021·山东·淄博市临淄区教学研究室八年级期末)如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
A. B.2 C. D.6
20.(2021·山东福山·八年级期末)如图,点是矩形的对角线上一点,过点作,分别交于,连接,若,则图中阴影部分的面积为( )
A. B.
C. D.
21.(2021·山东文登·八年级期末)矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,连接AG,取AG的中点H,连接EH.若,,则( )
A. B.2 C. D.
22.(2021·山东台儿庄·八年级期末)如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则DE的长为( )
A. B. C. D.
23.(2021·山东博兴·八年级期末)如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2,则AC的长为( )
A.2 B.4 C.6 D.8
24.(2021·山东武城·八年级期末)如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
25.(2021·山东陵城·八年级期末)如图,在平面直角坐标系中,四边形为菱形,,,,则对角线交点的坐标为( )
A. B. C. D.
26.(2021·山东福山·八年级期末)如图,菱形中,E,F分别是,的中点,若,则菱形的周长为( )
A.20 B.30 C.40 D.50
27.(2021·山东中区·八年级期末)如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )
A.1个 B.2个 C.3个 D.4个
28.(2021·山东金乡·八年级期末)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A. B. C.12 D.24
29.(2021·山东临淄·八年级期末)如图,菱形的边长为13,对角线,点E、F分别是边、的中点,连接并延长与的延长线相交于点G,则( )
A.13 B.10 C.12 D.5
30.(2021·山东中区·八年级期末)矩形具有而菱形不具有的性质是( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
31.(2021·山东安丘·八年级期末)如图,已知线段AB,分别以A,B为圆心,大于同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是( )
A.AB平分∠CAD B.CD平分∠ACB C.AB⊥CD D.AB=CD
32.(2021·山东槐荫·八年级期末)若顺次连接四边形ABCD各边的中点所得四边形是菱形.则四边形ABCD一定是 ( )
A.菱形 B.对角线互相垂直的四边形
C.矩形 D.对角线相等的四边形
33.(2021·山东临邑·八年级期末)如图,正方形的边长为4,点在上且,为对角线上一动点,则周长的最小值为( ).
A.5 B.6 C.7 D.8
34.(2021·山东阳信·八年级期末)如图,在长方形中无重叠放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( )
A. B. C. D.
35.(2021·山东东平·八年级期末)平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
36.(2021·山东禹城·八年级期末)如图,点O(0,0),A(0,1)是正方形的两个顶点,以对角线为边作正方形,再以正方形的对角线作正方形,…,依此规律,则点的坐标是( )
A.(-8,0) B.(0,8)
C.(0,8) D.(0,16)
37.(2021·山东蒙阴·八年级期末)下列命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相垂直且平分的四边形是菱形;
③一个角为90°且一组邻边相等的四边形是正方形;
④对角线相等的平行四边形是矩形.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
38.(2021·山东临淄·八年级期末)下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
39.(2021·山东福山·八年级期末)如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )
A.()n﹣1 B.2n﹣1 C.()n D.2n
二、填空题
40.(2021·山东莱州·八年级期末)如图,在 ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为__________.
41.(2021·山东滕州·八年级期末)如图,在中,过点C作,垂足为E,若,则的度数为____.
42.(2021·山东招远·八年级期末)如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=8,EF=1,则BC长为__________.
43.(2021·山东槐荫·八年级期末)如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连结OE.下列结论:
①∠CAD=30°;②S ABCD=AB·AC;③OB=AB;④OE=BC,成立的结论有______.(填序号)
44.(2021·山东莱州·八年级期末)如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
45.(2021·山东中区·八年级期末)如图,点的坐标为,点在轴上,把沿轴向右平移到,若四边形的面积为9,则点的坐标为_______.
46.(2021·山东台儿庄·八年级期末)如图,在平行四边形中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为______.
47.(2021·山东河口·八年级期末)如图,在平行四边形中,点为边上一点,,点,点分别是中点,若,则的长为__________.
48.(2021·山东滨州·八年级期末)如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件____,使四边形ABCD是平行四边形(填一个即可).
49.(2021·山东莱州·八年级期末)如图,平行四边形ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,连接AP,若S△PBG=2,则S四边形AEPH=_____.
50.(2021·山东桓台·八年级期末)如图,在矩形ABCD中,,,点E在边BC上,且.连接AE,将沿AE折叠,若点B的对应点落在矩形ABCD的边上,则 a的值为________.
51.(2021·山东蒙阴·八年级期末)如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是_____.
52.(2021·山东周村·八年级期末)如图,有一张长方形片ABCD,,.点E为CD上一点,将纸片沿AE折叠,BC的对应边恰好经过点D,则线段DE的长为________cm.
53.(2021·山东台儿庄·八年级期末)如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为_____.
54.(2021·山东沂源·八年级期末)如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=_____cm.
55.(2021·山东单县·八年级期末)如图,在菱形中,,点在上,若,则__________.
56.(2021·山东肥城·八年级期末)如图,在菱形中,对角线交于点,过点作于点,已知BO=4,S菱形ABCD=24,则___.
57.(2021·山东安丘·八年级期末)如图,将两张对边平行且相等的纸条交叉叠放在一起,则重合部分构成的四边形ABCD_________菱形(是,或不是).
58.(2021·山东蓬莱·八年级期末)如图,在菱形中,对角线相交于点O,点E在线段BO上,连接AE,若,,,则线段AE的长为_____.
59.(2021·山东泗水·八年级期末)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是___.
60.(2021·山东安丘·八年级期末)用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为____________(用含a,b的代数式表示).
61.(2021·山东莱州·八年级期末)如图,正方形的边长为4,点在上且,为对角线上一动点,则周长的最小值为_____________.
62.(2021·山东平阴·八年级期末)如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF.下列结论:①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP.其中正确的结论是__.(请填序号)
63.(2021·山东·日照市新营中学八年级期末)如图,在菱形ABCD中,,且,点F为对角线AC的动点,点E为AB上的动点,则的最小值为______.
64.(2021·山东文登·八年级期末)如图,在中,,,点D是AB上一动点,以AC为对角线的所有平行四边形ADCE中,DE的最小值是________.
三、解答题
65.(2021·山东长清·八年级期末)如图,在 ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.
66.(2021·山东罗庄·八年级期末)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连接DF
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
67.(2021·山东临淄·八年级期末)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
68.(2021·山东定陶·八年级期末)在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
69.(2021·山东郓城·八年级期末)如图,已知△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,EF=DC.
(1)求证:四边形EFCD是平行四边形.
(2)若BE=EF,求证:AE=AD.
70.(2021·山东福山·八年级期末)如图,在平行四边形中,对角线与交于点O,点M,N分别为、的中点,延长至点E,使,连接.
(1)求证:;
(2)若,且,,求四边形的面积.
71.(2021·山东崂山·八年级期末)如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
72.(2021·山东·东平县实验中学八年级期末)如图,在 ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
73.(2021·山东济南·八年级期末)已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF
求证:四边形BECF是平行四边形.
74.(2021·山东蓬莱·八年级期末)如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断 ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
75.(2021·山东鄄城·八年级期末)如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.
76.(2021·山东台儿庄·八年级期末)如图,点在一条直线上,.
(1)求证:;
(2)连接,求证:四边形是平行四边形.
77.(2021·山东博兴·八年级期末)如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
78.(2021·山东周村·八年级期末)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作,,垂足分别为E,F.AC平分.
(1)若,求的度数;
(2)求证:.
79.(2021·山东莱阳·八年级期末)如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD.
(1)求证:四边形ABCD是平行四边形;
(2)如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
80.(2021·山东金乡·八年级期末)如图,在 中,,过点 的直线MN//AB,为 边上一点,过点 作 ,垂足为点 ,交直线 于点 ,连接 ,.
(1)求证:;
(2)当 为 中点时,四边形 是什么特殊四边形 说明你的理由;
(3)在()的条件下,当 的大小满足什么条件时,四边形 是正方形 请说明你的理由.
81.(2021·山东莱芜·八年级期末)如图,在中,对角线与相交于点,点,分别在和的延长线上,且,连接,.
(1)求证:≌;
(2)连接,,当平分时,四边形是什么特殊四边形?请说明理由.
82.(2021·山东招远·八年级期末)如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
83.(2021·山东广饶·八年级期末)如图.在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形.
(2)若连接DE,交AC于点F,试判断四边形ABDE的形状(直接写出结果,不需要证明).
(3)△ABC再添加一个什么条件时,可使四边形ADCE是正方形.并证明你的结论.
84.(2021·山东德城·八年级期末)如图,在□ABCD中,∠BCD的平分线交直线AD于点F,∠BAD的平分线交DC延长线于E,交线段BC于H点
(1)证明:四边形AHCF是平行四边形;
(2)证明:AF=EC;
(3)若∠BAD=90°,G为CF的中点(如右图),判断△BEG的形状,并证明;
(4)在(3)的条件上,若已知AB=6,BC=7,试求△BEG的面积.
85.(2021·山东乳山·八年级期末)如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
86.(2021·山东周村·八年级期末)如图,在中,,中线,相交于点,点,分别为,的中点.
(1)求证:,;
(2)若,,求四边形的面积.
87.(2021·山东天桥·八年级期末)如图,在ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
88.(2021·山东张店·八年级期末)如图1,在中,点是边的中点,点在内,平分,,点在边上,.
(1)求证:四边形是平行四边形.
(2)判断线段、、的数量之间具有怎样的关系?证明你所得到的结论.
(3)点是的边上的一点,若的面积,请直接写出的面积(不需要写出解答过程).
试卷第1页,共3页
参考答案:
1.A
【分析】
此题涉及的知识点是平行四边形的性质.根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
【详解】
解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,DE=CD,
∴OE是△BCD的中位线,∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故选A
【点睛】
此题重点考察学生对于平行四边形的性质的理解,三角形的中位线,平行四边形的对角对边性质是解题的关键.
2.D
【分析】
确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
【详解】
只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
【点睛】
本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.
3.D
【详解】
由平行四边形的性质和三角形中位线定理得出选项A、B、C正确;由OB≠OC,得出∠OBE≠∠OCE,选项D错误;即可得出结论.
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB∥DC,
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE=DC,OE∥DC,
∴OE∥AB,
∴∠BOE=∠OBA,
∴选项A、B、C正确;
∵OB≠OC,
∴∠OBE≠∠OCE,
∴选项D错误;
故选D.
“点睛”此题考查了平行四边形的性质,还考查了三角形中位线定理,解决问题的方法是采用排除法解答.
4.B
【分析】
直接利用平行四边形的性质得出AO=CO,BO=DO,DC=AB=6,再利用已知求出AO+BO的长,进而得出答案.
【详解】
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,DC=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长是:14.
故选B.
【点睛】
平行四边形的性质掌握要熟练,找到等值代换即可求解.
5.C
【分析】
过点P作AD的垂线PF,交AD于F,再延长FP交BC于点E,表示出S1+ S2,得到即可.
【详解】
解:如图,过点P作AD的垂线PF,交AD于F,再延长FP交BC于点E,
根据平行四边形的性质可知PE⊥BC,AD=BC,
∴S1=AD×PF,S2=BC×PE,
∴S1+ S2
=AD×PF+BC×PE
=AD×(PE+PE)
=AD×EF
=S,
故选C.
【点睛】
本题考查了三角形的面积和平行四边形的性质,解题的关键是作出平行四边形过点P的高.
6.C
【分析】
根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出 ABCD的周长.
【详解】
解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=6,AB=CD,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵AD=6,BE=2,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴ ABCD的周长=6+6+4+4=20.
故选:C.
【点睛】
本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,熟练掌握平行四边形的性质,证明CE=CD是解题的关键.
7.B
【分析】
由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF与三角形ECF全等,得出AF=EF,即可求出AE的长.
【详解】
∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB,
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,又F为DC的中点,
∴DF=CF,
∴AD=DF=DC=AB=2,
在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,
∵平行四边形ABCD,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=4.
故选B.
考点:1.平行四边形的性质;2.等腰三角形的判定与性质;3.勾股定理.
8.C
【分析】
证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.
【详解】
解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
,
∴△BNA≌△BNE,
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19-BC=19-7=12,
∴DE=BE+CD-BC=5,
∴MN=DE=.
故选C.
【点睛】
本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
9.A
【分析】
过A作AH⊥BC于H,根据已知条件得到AE=CE,求得DE=BC,求得DF=AH,根据三角形的面积公式得到DE DF=2,得到AB AC=8,求得AB=2(负值舍去),根据勾股定理即可得到结论.
【详解】
解:过A作AH⊥BC于H,
∵D是AB的中点,
∴AD=BD,
∵DE∥BC,
∴AE=CE,
∴DE=BC,
∵DF⊥BC,
∴DF∥AH,DF⊥DE,
∴BF=HF,
∴DF=AH,
∵△DFE的面积为1,
∴DE DF=1,
∴DE DF=2,
∴BC AH=2DE 2DF=4×2=8,
∴AB AC=8,
∵AB=CE,
∴AB=AE=CE=AC,
∴AB 2AB=8,
∴AB=2(负值舍去),
∴AC=4,
∴BC=.
故选:A.
【点睛】
本题考查了三角形中位线定理,三角形的面积的计算,勾股定理,平行线的判定和性质,正确的识别图形是解题的关键.
10.A
【分析】
由,,分别为三条边的中点,可知DE、EF、DF为的中位线,即可得到的周长.
【详解】
解:如图,
∵,,分别为三条边的中点,
∴,,,
∵,
∴,
故选:A.
【点睛】
本题考查了三角形的中位线,熟练掌握三角形的中位线平行于第三边且是第三边的一半是解题的关键.
11.C
【分析】
根据平行四边形的性质得到AD∥BC,AB∥CD,求得DE∥BC,∠ABD=∠CDB,推出BD∥CE,于是得到四边形BCED为平行四边形,故A正确;根据平行线的性质得到∠DEF=∠CBF,根据全等三角形的性质得到EF=BF,于是得到四边形BCED为平行四边形,故B正确;根据平行线的性质得到∠AEB=∠CBF,求得∠CBF=∠BCD,求得CF=BF,同理,EF=DF,不能判定四边形BCED为平行四边形;故C错误;根据平行线的性质得到∠DEC+∠BCE=∠EDB+∠DBC=180°,推出∠BDE=∠BCE,于是得到四边形BCED为平行四边形,故D正确.
【详解】
∵四边形是平行四边形,
∴,,
∴,,
∵,
∴,
∴,
∴为平行四边形,故A正确;
∵,
∴,
在与中,
,
∴,
∴,
∵,
∴四边形为平行四边形,故B正确;
∵,
∴,
∵,
∴,
∴,
同理,,
∴不能判定四边形为平行四边形;故C错误;
∵,
∴,
∵,
∴,
∴四边形为平行四边形,故D正确,
故选C.
【点睛】
本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.
12.D
【分析】
把A、B、C、D四个选项分别作为添加条件进行验证,D为正确选项.添加D选项,即可证明△DEC≌△FEB,从而进一步证明DC=BF=AB,且DC∥AB.
【详解】
添加A、,无法得到AD∥BC或CD=BA,故错误;
添加B、,无法得到CD∥BA或,故错误;
添加C、,无法得到,故错误;
添加D、
∵,,,
∴,,∴,
∵,∴,
∴四边形是平行四边形.
故选D.
【点睛】
本题是一道探索性的试题,考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
13.C
【分析】
根据平行四边形的判定方法逐项分析即可.
【详解】
A. ∵ AB∥DC,AB=DC,∴四边形ABCD是平行四边形;
B. ∵ AB=DC,AD=BC,∴四边形ABCD是平行四边形;
C.等腰梯形ABCD满足 AB∥DC,AD=BC,但四边形ABCD是平行四边形;
D. OA=OC,OB=OD,∴四边形ABCD是平行四边形;
故选C.
【点睛】
本题主要考查了平行四边形的判定,平行四边形的判定方法有:①两组对边分别平行的四边形是平行四边形;②一组对边平行且相等的四边形是平行四边形;③两组对边分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤.两组对角分别相等的四边形是平行四边形.
14.A
【分析】
根据平行线的性质得到∠AEB=∠CBF,求得∠CBF=∠BCD,求得CF=BF,同理,EF=DF,不能判定四边形BCED为平行四边形;故A错误;根据平行线的性质得到∠DEF=∠CBF,根据全等三角形的性质得到DF=CF,于是得到四边形BCED为平行四边形,故B正确;根据平行四边形的性质得到AD∥BC,AB∥CD,求得DE∥BC,∠ABD=∠CDB,推出BD∥CE,于是得到四边形BCED为平行四边形,故C正确;根据平行线的性质得到∠DEC+∠BCE=∠EDB+∠DBC=180°,推出∠BDE=∠BCE,于是得到四边形BCED为平行四边形,故D正确.
【详解】
解:A、∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故A错误;
∵ DE∥BC,
∴∠DEF=∠CBF,
∠DEF=∠CBF
在△DEF与△CBF中,
∴△DEF△CBF(ASA),
∴DF=CF
∵EF=BF
∴四边形BCED为平行四边形,故B正确;
∵四边形ABCD是平行四边形,
∴ .AD∥BC,AB∥CD,
∴DE∥CE,∠ABD=∠CDB,
∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故C正确;
∵AEB∥C,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确.
故选:A.
【点睛】
本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.
15.C
【分析】
由,得出∠BAC=90°,则①正确;由等边三角形的性质得∠DAB=∠EAC=60°,则∠DAE=150°,由SAS证得△ABC≌△DBF,得AC=DF=AE=4,同理△ABC≌△EFC(SAS),得AB=EF=AD=3,得出四边形AEFD是平行四边形,则②正确;由平行四边形的性质得∠DFE=∠DAE=150°,则③正确;∠FDA=180°-∠DFE=30°,过点作于点,,则④不正确;即可得出结果.
【详解】
解:∵,
∴,
∴∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
又∴∠BAC=90°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
∴∠FDA=180°-∠DFE=180°-150°=30°,
过点作于点,
∴,
故④不正确;
∴正确的个数是3个,
故选:C.
【点睛】
本题考查了平行四边形的判定与性质、勾股定理的逆定理、全等三角形的判定与性质、等边三角形的性质、平角、周角、平行是四边形面积的计算等知识;熟练掌握平行四边形的判定与性质是解题的关键.
16.D
【详解】
试题分析:先根据矩形的特点求出BC的长,再由翻折变换的性质得出△CEF是直角三角形,利用勾股定理即可求出CF的长,再在△ABC中利用勾股定理即可求出AB的长.
解:∵四边形ABCD是矩形,AD=8,
∴BC=8,
∵△AEF是△AEB翻折而成,
∴BE=EF=3,AB=AF,△CEF是直角三角形,
∴CE=8﹣3=5,
在Rt△CEF中,CF===4,
设AB=x,
在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,
故选D.
考点:翻折变换(折叠问题);勾股定理.
17.C
【分析】
先证明再求解利用轴对称可得答案.
【详解】
解:由对折可得:
矩形,
BC=8
由对折得:
故选C.
【点睛】
本题考查的是矩形的性质,等腰三角形的判定,勾股定理的应用,轴对称的性质,掌握以上知识是解题的关键.
18.D
【详解】
根据折叠的性质知,四边形AFEB与四边形FDCE全等,有EC=AF=AE,
由勾股定理得,AB2+BE2=AE2即42+(8﹣AE)2=AE2,解得,AE=AF=5,BE=3,
作EG⊥AF于点G,则四边形AGEB是矩形,有AG=3,GF=2,GE=AB=4,由勾股定理得EF=.
故选D.
19.B
【分析】
先由题意得到大正方形的边长和小正方形的边长,再求阴影部分的面积.
【详解】
由题意可得,大正方形的边长为,小正方形的边长为,
∴图中阴影部分的面积为:,故选B.
【点睛】
本题考查矩形面积的求法,解题的关键是得到大正方形的边长和小正方形的边长.
20.A
【分析】
先根据矩形的性质证得,然后求解即可.
【详解】
解:作PM⊥AD于M,交BC于N,
∴四边形AEPM、四边形DFPM、四边形CFPN和四边形BEPN都是矩形,
∵,,,,,
∴S矩形DFPM=S矩形BEPN,
∵PM=AE=1,PF=NC=3,
∴,
∴S阴=,
故选:A.
【点睛】
本题主要考查矩形的性质、三角形的面积等知识,证得是解答本题的关键.
21.A
【分析】
延长GE交AB于点R,连接AE,设AG交DE于点M,过点E作EN⊥AG于N,先计算出RG=6,∠ARG=,AR=2,根据勾股定理求出,得到HG=,利用,求出,即可利用勾股定理求出NG、EH.
【详解】
如图,延长GE交AB于点R,连接AE,设AG交DE于点M,过点E作EN⊥AG于N,
∵矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,
∴RG=BF=BC+CF=2+4=6,∠ARG=,AR=AR-CE=4-2=2,
∴,
∵H是AG中点,
∴HG=,
∵,
∴,
∴,
在Rt△ENG中, ,
∴,
∴,
故选:A.
【点睛】
此题考查矩形的性质,勾股定理,线段中点的性质,三角形面积法求线段长度,熟记矩形的性质及熟练运用勾股定理是解题的关键.
22.B
【分析】
先根据矩形的性质得AD=BC=5,AB=CD=3,再根据折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=4,则CF=BC﹣BF=1,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理得到x2+12=(3﹣x)2,解方程即可得到DE的长.
【详解】
解:∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
在Rt△ABF中,BF===4,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则DE=EF=3﹣x,
在Rt△ECF中,CE2+FC2=EF2,
∴x2+12=(3﹣x)2,
解得x=,
∴DE=3﹣x=,
故选:B.
【点睛】
本题考查了翻折变换、矩形的性质、勾股定理等知识,属于常考题型,灵活运用这些性质进行推理与计算是解题的关键.
23.B
【分析】
已知四边形ABCD是矩形,∠AOD=120°,AB=2,根据矩形的性质可证得△AOB是等边三角形,则OA=OB=AB=2,AC=2OA=4.
【详解】
∵四边形ABCD是矩形
∴AC=BD,OA=OC,OB=OD
∴OA=OB
∵∠AOD=120°
∴∠AOB=60°
∴△AOB是等边三角形
∴OA=OB=AB=2
∴AC=2OA=4
故选:B
【点睛】
本题考查了矩形的基本性质,等边三角形的判定和性质.
24.C
【详解】
试题分析:连接EF交AC于点M,由四边形EGFH为菱形可得FM=EM,EF⊥AC;利用”AAS或ASA”易证△FMC≌△EMA,根据全等三角形的性质可得AM=MC;在Rt△ABC中,由勾股定理求得AC=,且tan∠BAC=;在Rt△AME中,AM=AC= ,tan∠BAC=可得EM=;在Rt△AME中,由勾股定理求得AE=5.故答案选C.
考点:菱形的性质;矩形的性质;勾股定理;锐角三角函数.
25.D
【分析】
过点作轴于点,由直角三角形的性质求出长和长即可.
【详解】
解:过点作轴于点,
∵四边形为菱形,,
∴,OB⊥AC,,
∵,∴,
∴,
∴,,
∴,
∴.
故选D.
【点睛】
本题考查了菱形的性质、勾股定理及含30°直角三角形的性质,正确作出辅助线是解题的关键.
26.C
【分析】
由题意可知EF为△ABD的中位线,可求出AB的长,由于菱形四条边相等即可得到周长.
【详解】
解:∵E,F分别是,的中点,
∴EF为△ABD的中位线,
∴,
∵四边形是菱形,
∴,
∴菱形的周长为
故选:C.
【点睛】
本题考查了三角形的中位线,菱形的性质,发现EF为△ABD的中位线是解题的关键.
27.C
【分析】
由折叠的性质可得四边形EBFG是菱形从而判断①②正确;由角平分线定理即可判断DG≠GH,由此推出③错误;根据F、C重合时的性质,可得∠AEB=30°,进而算出④正确.
【详解】
连接BE,由折叠可知BO=GO,
∵EG//BF,
∴∠EGO=∠FBO,
又∵∠EOG=∠FOB,
∴△EOG≌△FOB(ASA) ,
∴EG=BF,
∴四边形EBFG是平行四边形,
由折叠可知BE=EG,
则四边形EBFG为菱形,
故EF⊥BG,GE=GF,
∴①②正确;
∵四边形EBFG为菱形,
∴KG平分∠DGH,
∴,DG≠GH,
∴ S△GDK≠S△GKH,故③错误;
当点F与点C重合时,BE=BF=BC=12=2AB,
∴∠AEB=30°,,故④正确.
综合,正确的为①②④.
故选C.
【点睛】
本题考查矩形的性质,菱形的判断,折叠的性质,关键在于结合图形对线段和角度进行转换.
28.A
【详解】
解:如图,设对角线相交于点O,
∵AC=8,DB=6,∴AO=AC=×8=4,BO=BD=×6=3,
由勾股定理的,AB===5,
∵DH⊥AB,∴S菱形ABCD=AB DH=AC BD,
即5DH=×8×6,解得DH=.
故选A.
【点睛】
本题考查菱形的性质.
29.B
【分析】
连接对角线BD,交AC于点O,求证四边形BDEG是平行四边形,EG=BD,利用勾股定理求出OD的长,BD=2OD,即可求出EG.
【详解】
连接BD,交AC于点O,
由题意知:菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB=BC=CD=DA=13, EFBD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵ABCD,EFBD
∴DEBG,BDEG
在四边形BDEG中,
∵DEBG,BDEG
∴四边形BDEG是平行四边形
∴BD=EG
在△COD中,
∵OC⊥OD,CD=13,CO=12
∴OD=OB=5
∴BD=EG=10
故选B.
【点睛】
本题主要考查了菱形的性质,平行四边形的性质及勾股定理,熟练掌握菱形、平行四边形的性质和勾股定理是解题的关键.
30.A
【详解】
解:菱形的对角线互相平分、垂直、对角线平分一组对角,
矩形的对角线互相平分、相等,
∴矩形具有而菱形不具有的性质是对角线相等,
故选A.
考点:1.菱形的性质;2.矩形的性质.
31.D
【分析】
根据作图判断出四边形ACBD是菱形,再根据菱形的性质:菱形的对角线平分一组对角、菱形的对角线互相垂直平分可得出答案
【详解】
解:由作图知AC=AD=BC=BD,
∴四边形ACBD是菱形,
∴AB平分∠CAD、CD平分∠ACB、AB⊥CD,
不能判断AB=CD,
故选:D.
【点睛】
本题主要考查线段垂直平分线的尺规作图、菱形的判定方法等,解题的关键是掌握菱形的判定与性质.
32.D
【分析】
根据三角形的中位线定理得到EH∥FG,EF=FG,EF=BD,要是四边形为菱形,得出EF=EH,即可得到答案.
【详解】
解:∵E,F,G,H分别是边AD,DC,CB,AB的中点,
∴EH=AC,EH∥AC,FG=AC,FG∥AC,EF=BD,
∴EH∥FG,EF=FG,
∴四边形EFGH是平行四边形,
假设AC=BD,
∵EH=AC,EF=BD,
则EF=EH,
∴平行四边形EFGH是菱形,
即只有具备AC=BD即可推出四边形是菱形,
故选D.
33.B
【分析】
连接ED交AC于一点F,连接BF,根据正方形的对称性得到此时的周长最小,利用勾股定理求出DE即可得到答案.
【详解】
连接ED交AC于一点F,连接BF,
∵四边形ABCD是正方形,
∴点B与点D关于AC对称,
∴BF=DF,
∴的周长=BF+EF+BE=DE+BE,此时周长最小,
∵正方形的边长为4,
∴AD=AB=4,∠DAB=90°,
∵点在上且,
∴AE=3,
∴DE=,
∴的周长=5+1=6,
故选:B.
【点睛】
此题考查正方形的性质:四条边都相等,四个角都是直角以及正方形的对称性质,还考查了勾股定理的计算,依据对称性得到连接DE交AC于点F是的周长有最小值的思路是解题的关键.
34.B
【分析】
先根据正方形的面积公式求出两张正方形纸片的边长,从而可得长方形ABCD的长与宽,再利用长方形ABCD的面积减去两个正方形的面积即可得.
【详解】
面积为的正方形纸片的边长为,
则,
面积为的正方形纸片的边长为,
则,
因此,图中空白部分面积为,
故选:B.
【点睛】
本题考查了二次根式的几何应用,正确求出两个正方形的边长是解题关键.
35.A
【详解】
试题分析:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选A.
考点:特殊四边形的性质
36.D
【分析】
根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以,可求出从A到A3变化后的坐标,再求出A1、A2、A3、A4、A5,继而得出A8坐标即可.
【详解】
解:根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘,
∵从A到经过了3次变化,
∵45°×3=135°,1×=2,
∴点所在的正方形的边长为2,点位置在第四象限,
∴点的坐标是(2,-2),
可得出:点坐标为(1,1),
点坐标为(0,2),点坐标为(2,-2),
点坐标为(0,-4),点坐标为(-4,-4),
(-8,0),A7(-8,8),(0,16),
故选D.
【点睛】
本题考查了规律题,点的坐标,观察出每一次的变化特征是解答本题的关键.
37.B
【分析】
根据平行四边形的判定,菱形的判定,正方形的判定,矩形的判定逐一判断即可.
【详解】
解:①一组对边平行,另一组对边相等的四边形是平行四边形,是假命题;
②对角线互相垂直且平分的四边形是菱形,是真命题;
③一个角为90°且一组邻边相等的四边形是正方形,是假命题;
④对角线相等的平行四边形是矩形,是真命题.
故选:B.
【点睛】
本题考查了平行四边形、菱形、正方形、矩形的判定,熟知特殊四边形的判定定理是解题关键.
38.B
【分析】
利用平行四边形的判定、菱形的判定、矩形的判定及正方形的判定定理对各选项逐一判断后即可确定正确的选项.
【详解】
解:A、一组对边平行,另一组对边相等的四边形是平行四边形错误,如等腰梯形;
B、对角线互相垂直平分的四边形是菱形,正确;
C、对角线相等的四边形是矩形错误,如等腰梯形;
D、对角线互相垂直且相等的四边形是正方形错误,如一般四边形对角线也可以互相垂直且相等.
故选:B.
【点睛】
本题考查了命题与定理,解题的关键是了解平行四边形的判定、菱形的判定、矩形的判定及正方形的判定定理,难度一般.
39.B
【详解】
【分析】先求出第一个正方形面积、第二个正方形面积、第三个正方形面积,…探究规律后,即可解决问题.
【详解】第一个正方形的面积为1=20,
第二个正方形的面积为()2=2=21,
第三个正方形的边长为22,
…
第n个正方形的面积为2n﹣1,
故选B.
【点睛】本题考查了规律型:图形的变化类,正方形的性质,根据前后正方形边长之间的关系找到Sn的规律是解题的关键.
40.30°.
【详解】
∵四边形ABCD是平行四边形
∴AB∥DC,∠ABC=∠D
∴∠DAB+∠D=180°,
∵∠D=100°,
∴∠DAB=80°, ∠ABC=100°
又∵∠DAB的平分线交DC于点E
∴∠EAD=∠EAB=40°
∵AE=AB
∴∠ABE=(180°-40°)=70°
∴∠EBC=∠ABC-∠ABE=100°-70°=30°.
考点:1.角平分线的性质;2.平行四边形的性质.
41.50°
【分析】
由平行四边形的性质得出∠B=∠EAD=40°,由角的互余关系得出∠BCE=90°-∠B即可.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠EAD=40°,
∵CE⊥AB,
∴∠BCE=90°-∠B=50°;
故答案为:50°.
【点睛】
本题考查了平行四边形的性质和三角形的内角和;熟练掌握平行四边形的性质,求出∠B的度数是解决问题的关键.
42.15
【分析】
由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB=8,同理可得DE=DC=8,再由EF的长,即可求出BC的长.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=8,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=8,
同理可证:DE=DC=8,
∵EF=AF+DE-AD=1,
即8+8-AD=1,
解得:AD=15;
故答案为:15.
【点睛】
本题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出AF=AB是解决问题的关键.
43.①②④
【分析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S ABCD=AB AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.
【详解】
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE=AB,
∴OE=BC,故④正确.
故答案为①②④.
【点睛】
本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式,熟练掌握性质定理和判定定理是解题的关键.
44.14.5
【分析】
根据平行四边形的性质易证三角形全等,进而易得AE=CF,故四边形的周长=AD+CD+EF,根据已知求解即可.
【详解】
解:在平行四边形ABCD中,AD∥BC,AC与BD互相平分
∴AO=OC,∠DAC=∠ACB,∠AOE=∠COF
∴△AOE≌△COF
∴AE=CF,OF=OE=2.5
∴四边形的周长=CF+DE+CD+EF
=AE+DE+CD+EF
=AD+CD+EF
=×2
=14.5.
故答案为:14.5.
【点睛】
本题考查了平行四边形的性质以及三角形全等的证明,将所求线段转化为已知线段是解题的关键.
45.(4,3)
【分析】
过点A作AH⊥x轴于点H,得到AH=3,根据平移的性质证明四边形ABDC是平行四边形,得到AC=BD,根据平行四边形的面积是9得到,求出BD即可得到答案.
【详解】
过点A作AH⊥x轴于点H,
∵A(1,3),
∴AH=3,
由平移得AB∥CD,AB=CD,
∴四边形ABDC是平行四边形,
∴AC=BD,
∵,
∴BD=3,
∴AC=3,
∴C(4,3)
故答案为:(4,3).
【点睛】
此题考查平移的性质,平行四边形的判定及性质,直角坐标系中点到坐标轴的距离与点坐标的关系.
46.16
【分析】
根据平行线的性质和角平分线的性质,得到∠BEC=90°,然后利用勾股定理,即可求出答案.
【详解】
解:如图,在平行四边形中,
∴,AD=BC,AD∥BC,AB∥CD,
∴∠AEB=∠CBE,∠DEC=∠BCE,∠ABC+∠DCB=180°
∵BE、CE分别是∠ABC和∠DCB的角平分线,
∴∠ABE=∠CBE,∠DCE=∠BCE,
∴∠AEB=∠ABE,∠DEC =∠DCE,∠CBE+∠BCE=90°
∴AB=AE=2,DE=DC=2,∠BEC=90°,
∴AD=2+2=4,
∴BC=AD=4,
在Rt△BCE中,由勾股定理,得
;
故答案为:16.
【点睛】
本题考查了平行四边形的性质,勾股定理,平行线的性质,角平分线的性质,解题的关键是熟练掌握所学的性质,正确求出角之间的关系进行解题.
47.8
【分析】
先根据三角形中位线定理可得BC的长,再根据平行四边形的性质可得AD的长,然后根据即可得.
【详解】
点,点分别是中点
是的中位线
四边形ABCD是平行四边形
又
故答案为:8.
【点睛】
本题考查了三角形中位线定理、平行四边形的性质等知识点,熟记三角形中位线定理是解题关键.
48.AD=BC(答案不唯一)
【分析】
根据平行四边形的判定方法添加一个条件即可.
【详解】
解:根据一组对边平行且相等的四边形是平行四边形,可以添加条件AD=BC,
根据两组对边分别平行的四边形是平行四边形,可以添加条件AB∥DC,
本题只需添加一个即可,
故答案为:AD=BC(答案不唯一).
【点睛】
本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
49.8
【分析】
由题意根据平行四边形的判定和性质,进行面积的等量代换分析即可求解.
【详解】
解:∵EF∥BC,GH∥AB,
∴四边形HPFD、四边形PGCF、四边形BGPE是平行四边形,
∴,
∵S△PBG=2,
∴,
∵CG=2BG,
∴,
∵,
∴.
故答案为:8.
【点睛】
本题考查的是平行四边形的判定和性质,熟练掌握平行四边形的性质定理是解题的关键.
50.或
【分析】
分两种情况:①点落在AD边上,根据矩形与折叠的性质易得,即可求出a的值;②点落在CD边上,证明,根据相似三角形对应边成比例即可求出a的值.
【详解】
解:分两种情况:
①当点落在AD边上时,如图1.
四边形ABCD是矩形,
,
将沿AE折叠,点B的对应点落在AD边上,
,
,
,
;
②当点落在CD边上时,如图2.
∵四边形ABCD是矩形,
,.
将沿AE折叠,点B的对应点落在CD边上,
,,,
,.
在与中,
,
,
,即,
解得,(舍去).
综上,所求a的值为或.
故答案为或.
【点睛】
本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.
51.(-10,3)
【详解】
试题分析:根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE,设CE=x,则BE=8-x,然后根据折叠的性质,可得EF=8-x,根据勾股定理可得,解得x=3,则OF=6,所以OC=10,由此可得点E的坐标为(-10,3).
故答案为:(-10,3)
52.5
【分析】
根据折叠的性质得到线段和角相等,然后在Rt△中,由勾股定理求出的长,则可得出的长,再在Rt△利用勾股定理进行计算即可求DE的长.
【详解】
解:∵四边形ABCD是长方形,
∴AD=BC=10,CD=AB=8,∠B=∠C=90°.
根据折叠的性质,得 =8-DE, ,∠=∠B=90°.
在Rt△中,由勾股定理,得==6.
∴=10-6=4.
在Rt△中,由勾股定理,得.
∴(8-DE)2+42=DE2.
解得DE=5.
故答案是:5.
【点睛】
本题考查了折叠的性质,矩形的性质,勾股定理,熟练运用折叠的性质是本题的关键.
53.
【分析】
设CE=x,则BE=6﹣x由折叠性质可知,EF=CE=x,DF=CD=AB=10,所以AF=8,BF=AB﹣AF=10﹣8=2,在Rt△BEF中,BE2+BF2=EF2,即(6﹣x)2+22=x2,解得x=.
【详解】
解:设CE=x,则BE=6﹣x由折叠性质可知,EF=CE=x,DF=CD=AB=10,
在Rt△DAF中,AD=6,DF=10,
∴AF=8,
∴BF=AB﹣AF=10﹣8=2,
在Rt△BEF中,BE2+BF2=EF2,
即(6﹣x)2+22=x2,
解得x=,
故答案为.
【点睛】
本题考查了矩形,熟练掌握矩形的性质以及勾股定理是解题的关键.
54.5
【详解】
连接AC,FC,求出AC,利用三角形的中位线定理解决问题即可.
【解答】解:连接AC,FC.
由翻折的性质可知,BE垂直平分线段CF,
∴FM⊥BE,∴F.M,C共线,FM=MC,
∵AN=FN,∴MN=AC,
∵四边形ABCD是矩形,∴∠ABC=90°,
∴AC===10(cm),∴MN=AC=5(cm),
故答案为5.
【点评】本题考查翻折变换,矩形的性质,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题,属于中考常考题型.
55.115°
【分析】
先根据菱形性质求出∠BCD,∠ACE,再根据求出∠AEC,最后根据两直线平行,同旁内角互补解题即可.
【详解】
解:四边形ABCD是菱形,,
∴AB∥CD,
∴∠BCD=180°-∠B=130°,∠ACE=∠BCD=65°,
∵ ,
∴∠ACE=∠AEC=65°,
∴∠BAE=180°-∠AEC=115°.
【点睛】
本题考查了菱形性质,等腰三角形性质,解题方法较多,根据菱形性质求解∠ACE是解题关键.
56.
【分析】
根据菱形面积=对角线积的一半可求,再根据勾股定理求出,然后由菱形的面积即可得出结果.
【详解】
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴;
故答案为.
【点睛】
本题考查了菱形的性质、勾股定理以及菱形面积公式.熟练掌握菱形的性质,由勾股定理求出是解题的关键.
57.是
【分析】
如图(见解析),先根据“两张对边平行且相等的纸条”得出,再根据平行四边形的判定可得四边形ABCD是平行四边形,然后根据三角形全等的判定定理与性质可得,最后根据菱形的判定即可得.
【详解】
如图,过点B作,交DA延长线于点E,过点D作,交BA延长线于点F
由题意得:
四边形ABCD是平行四边形
在和中,
平行四边形ABCD是菱形
故答案为:是.
【点睛】
本题考查了平行四边形与菱形的判定、三角形全等的判定定理与性质等知识点,熟练掌握平行四边形与菱形的判定是解题关键.
58.
【分析】
设BE=x,根据菱形性质可得到AB= AD=CD=2x,进而得到,解得x值,根据勾股定理即可求得AE值.
【详解】
解:设BE=x,
∵菱形,
∴AB= AD=CD=2x,
∵,
∴,
∴BD=3x,
∴OB=OD=,
∴,
∴x=2,
∴AB=4,BE=2,
∴,
∴,
故答案为:.
【点睛】
本题考查菱形的性质结合勾股定理的应用,熟练掌握菱形性质是解题的关键.
59.
【详解】
试题分析:连接DB,BD与AC相交于点M,
∵四边形ABCD是菱形,∴AD=AB.AC⊥DB.
∵∠DAB=60°,∴△ADB是等边三角形.
∴DB=AD=1,∴BM=
∴AM=
∴AC=.
同理可得AE=AC=()2,AG=AE=()3,…
按此规律所作的第n个菱形的边长为()n-1
60.
【分析】
如图,连接AE、AF,先证明△GAE≌△HAF,由此可证得,进而同理可得,根据正方形ABCD的面积等于四个相同四边形的面积之和及小正方形的面积即可求得答案.
【详解】
解:如图,连接AE、AF,
∵点A为大正方形的中心,
∴AE=AF,∠EAF=90°,
∴∠AEF=∠AFE=45°,
∵∠GEF=90°,
∴∠AEG=∠GEF-∠AEF=45°,
∴∠AEG=∠AFE,
∵四边形ABCD为正方形,
∴∠DAB=∠EAF=90°,
∴∠GAE=∠HAF,
在△GAE与△HAF中,
∴△GAE≌△HAF(ASA),
∴,
∴,
即,
∵,
∴,
∴同理可得:,
即,
故答案为:.
【点睛】
本题考查了正方形的性质及全等三角形的判定及性质,熟练掌握正方形的性质并能作出正确的辅助线是解决本题的关键.
61.6
【分析】
连接ED交AC于一点F,连接BF,根据正方形的对称性得到此时△BFE的周长最小,利用勾股定理求出DE即可得到答案.
【详解】
解:连接ED交AC于一点F,连接BF,
∵四边形ABCD是正方形,
∴点B与点D关于AC对称,
∴BF=DF,
∴的周长=BF+EF+BE=DE+BE,此时周长最小,
∵正方形的边长为4,
∴AD=AB=4,∠DAB=90°,
∵点在上且,
∴AE=3,
∴DE=,
∴的周长=5+1=6,
故答案为:6.
【点睛】
此题主要考查了正方形的性质,依据正方形的对称性,连接DE交AC于点F时△BFE的周长有最小值是解题的关键.
62.①②④
【分析】
用正方形的性质和垂直的定义判断出四边形PECF是矩形,从而判定②正确;直接用正方形的性质和垂直得出①正确,利用全等三角形和矩形的性质得出④正确,由点P是正方形对角线上任意一点,说明AD和PD不一定相等,得出③错误.
【详解】
如图,
∵P为正方形ABCD的对角线BD上任一点,
∴PA=PC,∠C=90°,
∵过点P作PE⊥BC于点E,PF⊥CD,
∴∠PEC=∠DFP=∠PFC=∠C=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴PA=EF,故②正确,
∵BD是正方形ABCD的对角线,
∴∠ABD=∠BDC=∠DBC=45°,
∵∠PFC=∠C=90°,
∴PF∥BC,
∴∠DPF=45°,
∵∠DFP=90°,
∴△FPD是等腰直角三角形,故①正确,
在△PAB和△PCB中,
,
∴△PAB≌△PCB,
∴∠BAP=∠BCP,
在矩形PECF中,∠PFE=∠FPC=∠BCP,
∴∠PFE=∠BAP.故④正确,
∵点P是正方形对角线BD上任意一点,
∴AD不一定等于PD,
只有∠BAP=22.5°时,AD=PD,故③错误,
故答案为①②④.
【点睛】
考查了正方形的性质,矩形的判定和性质,全等三角形的判定和性质,垂直的定义,解本题的关键是判断出四边形PECF是矩形.
63.
【分析】
连接BD、DF,作于由B、D关于AC对称,推出,推出,根据垂线段最短可知,当D、F、E共线,且与DH重合时,的值最小,最小值为DH的长;
【详解】
解:连接BD、DF,作于H.
四边形ABCD是菱形,
,,
是等边三角形,
、D关于AC对称,
,
,
根据垂线段最短可知,当D、F、E共线,且与DH重合时,的值最小,最小值为DH的长,
在中,,
故答案为.
【点睛】
本题考查轴对称最短问题、菱形的性质、勾股定理、垂线段最短等知识,解题的关键是学会添加常用辅助线,学会利用垂线段最短解决最短问题.
64.2
【分析】
平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥AB时,OD最小,即DE最小,根据直角三角形勾股定理即可求解.
【详解】
解:如图
∵平行四边形ADCE的对角线的交点是AC的中点O,又AB=AC=4
∴OC=OA=AC=2
当OD⊥AB时,OD最小,即DE最小.
∵OD⊥BA,∠BAC=45°,
∴∠AOD=45°
∴△ADO为等腰直角三角形
在Rt△ADO由勾股定理可知
OD= AO=
∴DE=2OD=2
故答案为:2.
【点睛】
本题考查了勾股定理,平行四边形的性质,即平行四边形对角线互相平分,正确理解DE最小值的条件是关键.
65.证明见解析.
【分析】
利用平行四边形的性质得出 AO=CO,AD∥BC,进而得出∠EAC=∠FCO, 再利用 ASA 求出△AOE≌△COF,即可得出答案.
【详解】
∵ ABCD 的对角线 AC,BD 交于点 O,
∴AO=CO,AD∥BC,
∴∠EAC=∠FCO,
在△AOE 和△COF 中,
∴△AOE≌△COF(ASA),
∴AE=CF.
【点睛】
本题考查了全等三角形的判定与性质以及平行四边形的性质,熟练掌握全等三角形的判定方法是解题关键.
66.证明见解析.
【分析】
(1)一方面Rt△ABC中,由∠BAC=30°可以得到AB=2BC,另一方面△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,从而可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF.
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
【详解】
证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC.
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.
∵在Rt△AFE和Rt△BCA中,AF=BC,AE=BA,
∴△AFE≌△BCA(HL).∴AC=EF.
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD.
∴∠DAB=∠DAC+∠BAC=90°.∴EF∥AD.
∵AC=EF,AC=AD,∴EF=AD.
∴四边形ADFE是平行四边形.
考点:1.全等三角形的判定与性质;2.等边三角形的性质;3.平行四边形的判定.
67.(1)见解析;(2)OE=5,BG=2.
【分析】
(1)先证明EO是△DAB的中位线,再结合已知条件OG∥EF,得到四边形OEFG是平行四边形,再由条件EF⊥AB,得到四边形OEFG是矩形;
(2)先求出AE=5,由勾股定理进而得到AF=3,再由中位线定理得到OE=AB=AD=5,得到FG=5,最后BG=AB-AF-FG=2.
【详解】
解:(1)证明:∵四边形ABCD为菱形,
∴点O为BD的中点,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴OE∥FG,
∵OG∥EF,∴四边形OEFG为平行四边形
∵EF⊥AB,∴平行四边形OEFG为矩形.
(2)∵点E为AD的中点,AD=10,
∴AE=
∵∠EFA=90°,EF=4,
∴在Rt△AEF中,.
∵四边形ABCD为菱形,
∴AB=AD=10,
∴OE=AB=5,
∵四边形OEFG为矩形,
∴FG=OE=5,
∴BG=AB-AF-FG=10-3-5=2.
故答案为:OE=5,BG=2.
【点睛】
本题考查了矩形的性质和判定,菱形的性质、勾股定理等知识点,特殊四边形的性质和判定属于中考常考题型,需要重点掌握.
68.(1)15°;(2)证明见解析.
【分析】
(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;
(2)如图2,利用直角三角形斜边上的中线性质得到BF=AC,利用含30度的直角三角形三边的关系得到BC=AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
【详解】
解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=(180° 30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75° 60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠BAC=30°,
∴BC=AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.
69.见解析
【详解】
(1)由△ABC是等边三角形得到∠B=60°,而∠EFB=60°,由此可以证明EF∥DC,而DC=EF,然后即可证明四边形EFCD是平行四边形;
(2)如图,连接BE,由BF=EF,∠EFB=60°可以推出△EFB是等边三角形,然后得到EB=EF,∠EBF=60°,而DC=EF,由此得到EB=DC,又
△ABC是等边三角形,所以得到∠ACB=60°,AB=AC,然后即可证明△AEB≌△ADC,利用全等三角形的性质就证明AE=AD.
试题解析:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC(内错角相等,两直线平行),
∵DC=EF,
∴四边形EFCD是平行四边形;
(2)连接BE
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠EBF=60°
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠EBF=∠ACB,
∴△AEB≌△ADC,
∴AE=AD.
考点:1.平行四边形的判定;2.全等三角形的判定与性质;3.等边三角形的性质.
70.(1)见解析;(2)24
【分析】
(1)由四边形ABCD是平行四边形得出AB=CD,ABCD,进而得到∠BAC=∠DCA,再结合AO=CO,M,N分别是OA和OC中点即可求解;
(2)证明△ABO是等腰三角形,结合M是AO的中点,得到∠BMO=∠EMO=90°,同时△DOC也是等腰三角形,N是OC中点,得到∠DNO=90°,得到EMDN,再由(1)得到EM=DN,得出四边形EMND为矩形,进而求出面积.
【详解】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,ABCD,OA=OC,
∴∠BAC=∠DCA,
又点M,N分别为、的中点,
∴,
在和中,
,
∴.
(2)BD=2BO,又已知BD=2AB,
∴BO=AB,∴△ABO为等腰三角形;
又M为AO的中点,
∴由等腰三角形的“三线合一”性质可知:BM⊥AO,
∴∠BMO=∠EMO=90°,
同理可证△DOC也为等腰三角形,
又N是OC的中点,
∴由等腰三角形的“三线合一”性质可知:DN⊥CO,
∠DNO=90°,
∵∠EMO+∠DNO=90°+90°=180°,
∴EMDN,
又已知EM=BM,由(1)中知BM=DN,
∴EM=DN,
∴四边形EMND为平行四边形,
又∠EMO=90°,∴四边形EMND为矩形,
在Rt△ABM中,由勾股定理有:,
∴AM=CN=3,
∴MN=MO+ON=AM+CN=3+3=6,
∴.
故答案为:.
【点睛】
本题考查了平行四边形的性质、矩形的判定和性质、矩形的面积公式等,熟练掌握其性质和判定方法是解决此类题的关键.
71.(1)∠APB=90°; (2)△APB的周长是24cm.
【详解】
【分析】(1)根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB即可;
(2)求出AD=DP=5,BC=PC=5,求出DC=10=AB,即可求出答案.
【详解】(1)∵四边形是平行四边形,
∴∥ ,∥, ,
∴ ,
又∵和分别平分和,
∴ ,
∴ ;
(2) ∵平分,∥ ,
∴ ,
∴ ,同理: ,
∴ ,
在中, , ∴ ,
∴△的周长.
【点睛】本题考查了平行四边形的性质,等腰三角形的判定与性质等,熟练掌握平行四边形的性质是解题的关键.
72.(1)详见解析;(2)13.
【分析】
(1)只要证明DN∥BM,DM∥BN即可;
(2)只要证明△CEM≌△AFN,可得FN=EM=5,在Rt△AFN中,根据勾股定理AN=即可解决问题.
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN===13.
【点睛】
本题考查平行四边形的性质和判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
73.证明见解析.
【分析】
根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形式平行四边形,可得证明结论.
【详解】
如答图,连接BC,设对角线交于点O.
∵四边形ABCD是平行四边形,∴OA=OD,OB=OC.
∵AE=DF,OA﹣AE=OD﹣DF,∴OE=OF.
∴四边形BEDF是平行四边形.
74.(1)证明见解析;(2) ADEF的形状为菱形,理由见解析;(3)四边形AEGF是矩形,理由见解析.
【分析】
(1)根据平行线的性质得到∠BDE=∠A,根据题意得到∠DEF=∠BDE,根据平行线的判定定理得到AD∥EF,根据平行四边形的判定定理证明;
(2)根据三角形中位线定理得到DE=AC,得到AD=DE,根据菱形的判定定理证明;
(3)根据等腰三角形的性质得到AE⊥EG,根据有一个角是直角的平行四边形是矩形证明.
【详解】
(1)证明:∵DE∥AC,
∴∠BDE=∠A,
∵∠DEF=∠A,
∴∠DEF=∠BDE,
∴AD∥EF,又∵DE∥AC,
∴四边形ADEF为平行四边形;
(2)解:□ADEF的形状为菱形,
理由如下:∵点D为AB中点,
∴AD=AB,
∵DE∥AC,点D为AB中点,
∴DE=AC,
∵AB=AC,
∴AD=DE,
∴平行四边形ADEF为菱形,
(3)四边形AEGF是矩形,
理由如下:由(1)得,四边形ADEF为平行四边形,
∴AF∥DE,AF=DE,
∵EG=DE,
∴AF∥DE,AF=GE,
∴四边形AEGF是平行四边形,
∵AD=AG,EG=DE,
∴AE⊥EG,
∴四边形AEGF是矩形.
故答案为(1)证明见解析;(2)菱形;(3)矩形.
【点睛】
本题考查的是平行四边形、矩形、菱形的判定,掌握它们的判定定理是解题的关键.
75.证明见解析
【分析】
(1)利用平行四边形的性质得出∠5=∠3,∠AEB=∠4,进而利用全等三角形的判定得出即可;
(2)利用全等三角形的性质得出AE=CF,进而得出四边形AECF是平行四边形,即可得出答案.
【详解】
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
76.(1)见解析;(2)见解析.
【分析】
(1)先证明,再利用SSS证明;
(2)根据“一组对边平行且相等的四边形是平行四边形”证明四边形是平行四边形即可.
【详解】
证明:
即
证明:
四边形是平行四边形.
【点睛】
本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形的判定方法,证明三角形全等是解决问题的关键.
77.(1)证明见解析;(2).
【分析】
(1)由平行四边形的判定得出四边形OCED是平行四边形,根据矩形的性质求出OC=OD,根据菱形的判定得出即可.(2)解直角三角形求出BC=2.AB=DC=2,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=BC=1,求出OE=2OF=2,求出菱形的面积即可.
【详解】
证明:,,
四边形OCED是平行四边形,
矩形ABCD,,,,
,
四边形OCED是菱形;
在矩形ABCD中,,,,
,
,
连接OE,交CD于点F,
四边形OCED为菱形,
为CD中点,
为BD中点,
,
,
.
【点睛】
本题主要考查了矩形的性质和菱形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:菱形的面积等于对角线积的一半.
78.(1);(2)见解析
【分析】
(1)利用三角形内角和定理求出,利用角平分线的定义求出,再利用平行线的性质解决问题即可.
(2)证明可得结论.
【详解】
(1)解:,
,
,
,
平分,
,
四边形是平行四边形,
,
,
(2)证明:四边形是平行四边形,
,
,,
,
,
,
.
【点睛】
本题考查平行四边形的性质,全等三角形的判定和性质等知识,解题的关键是熟练掌握相关的知识点.
79.(1)见解析 (2)9
【分析】
(1)先证明Rt△ABE≌Rt△CDF,得到AB∥CD,即可判定平行四边形;
(2)证明AB=GB,根据勾股定理构造方程,解方程即可求解.
【详解】
解:(1)∵AF=CE,
∴AF-EF=CE-EF,
∴AE=CF,
∵BE⊥AC,DF⊥AC,,
∴∠AEB=∠CFD=90°,
∵AB=CD,
∴Rt△ABE≌Rt△CDF,
∴∠BAE=∠DCF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,∠DAB=∠BCD,
∴∠AGB=∠GBC,
∵∠GBC=∠BCD,
∴∠AGB=∠BAG,
∴AB=GB,
设AB=GB=x,则BE=x-2,
∵BG⊥AC,
∴,
∴ ,
解得x=9,
∴AB=9.
【点睛】
本题考查了平行四边的判定与性质,勾股定理,等腰三角形判定等知识,综合性较强,熟知相关定理并根据已知条件合理选择定理是解题关键.
80.(1)见解析;(2)四边形 是菱形,理由见解析;(3)当 时,四边形 是正方形.理由见解析.
【分析】
(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)当=45°,由()可知,四边形 是菱形,可得,则四边形BECD是正方形.
【详解】
(1) ,
,
,
,
,
,即 ,
四边形 是平行四边形,
.
(2) 四边形 是菱形,
理由是: 点 为 中点,
,
,
,
,
四边形 是平行四边形,
,点 为 中点,
,
四边形 是菱形.
(3) 当 时,
,
,
由()可知,四边形 是菱形,
,
,
四边形 是正方形.
【点睛】
本题考查了平行四边形的性质和判定,菱形的判定,正方形的判定、直角三角形的性质的应用,灵活运用所学知识解决问题是解题的关键.
81.(1)见解析(2)菱形,见解析
【分析】
(1)利用SAS证明≌即可求解;
(2)先证明四边形是平行四边形,再证明对角线互相垂直即可得到为菱形.
【详解】
(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠ADB=∠CBD,
又∵∠ADB+∠ADE=180°,∠CBF+∠CBD=180°,
∴∠ADE=∠CBF
在△ADE和△CBF中
∴△ADE≌△CBF;
(2)四边形是菱形
理由如下:
如图,连接,,
由(1)得△ADE≌△CBF
∴CF=AE, ∠E=∠F
∴AE∥CF
∴AECF
∴四边形AFCE是平行四边形
当BD平分∠ABC时,∠ABD=∠CBD
又∵AD∥CB,
∴∠ADB=∠DBC
∴∠ABD=∠ABD
∴AD=AB=BC
∴△ABC为等腰三角形
由等腰三角形性质三线合一可得AC⊥EF
∴平行四边形AFCE是菱形
【点睛】
此题主要考查特殊平行四边形的性质与判定,解题的关键是熟知菱形的判定定理.
82.(1)见解析;(2)见解析
【分析】
(1)根据平行四边形的性质得到AB=CD,∠DAE=∠AEB,利用AE平分∠BAD,推出∠BAE=∠AEB,得到BE=AB,即可得到结论;
(2)根据BE=AB,BF平分∠ABE,得到AF=EF,证明△ADF≌△ECF,推出DF=CF,即可得到结论.
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF,
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
【点睛】
此题考查平行四边形的判定及性质,全等三角形的判定及性质,等腰三角形三线合一的性质,熟记各知识点并应用解决问题是解题的关键.
83.(1)证明见解析;(2)四边形ABDE是平行四边形;(3)当∠BAC=90°时,四边形ADCE是正方形,证明见解析
【分析】
(1)由等腰三角形的性质可得AD⊥BC,∠BAD=∠CAD,又由AN为△ABC的外角∠CAM的平分线,可得∠DAE=90°,又由CE⊥AN,由矩形的判定可证四边形ADCE为矩形;
(2)利用(1)中矩形的对角线相等推知:AC=DE;结合已知条件可以推知AB∥DE,又AE=BD,则易判定四边形ABDE是平行四边形;
(3)由等腰直角三角形的性质可得AD=CD=BD,即可证四边形ADCE是正方形.
【详解】
证明:(1)∵在△ABC中,AB=AC,AD为∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)四边形ABDE是平行四边形,
理由如下:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形;
(3)当∠BAC=90°时,四边形ADCE是正方形,
理由:∵∠BAC=90°,AB=AC,AD为∠BAC的平分线,
∴AD=CD=BD,
又∵四边形ADCE是矩形,
∴四边形ADCE是正方形.
【点睛】
本题考查平行四边形、矩形和正方形的判定方法,掌握特殊四边形的判定定理是解题的关键.
84.(1)证明见解析;(2)证明见解析;(3)等腰直角三角形,证明见解析;(4)12.5.
【分析】
【详解】
(1)由平行四边形的性质得出,∠BAD=∠BCD,BC∥AD,证出∠1=∠2,再证出∠2=∠3,得出AE∥CF,即可得出结论;
(2)由四边形AHCF是平行四边形,得出AF=CH,再证出CH=EC,即可得出AF=EC;
(3)连接AG,过G作GN∥BC交AB于N,先证四边形ABCD是矩形,得出∠GNB=90°,BC∥GN∥AD,再证出NG是AB的垂直平分线,得出BG=AG,得出∠BGN=∠AGN,然后证明△AFG≌△ECG,得出AG=EG=BG,∠EGC=∠AGF,∠GAF=∠GEC,再证出∠BGE=90°,即可得出结论;
(4)作GM⊥AD于M,则GM∥CD,由矩形的性质得出∠D=∠BCD=90°,CD=AB,AD=BC,再证出△DCF、△MGF是等腰直角三角形,得出FD=CD=6,GM=FM,证明GM为△DCF的中位线,得出FM=GM═DM=CD=3,求出AM,由勾股定理求出AG,得出BG、EG,即可求出△BEG的面积.
(1)证明:如图1所示:
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,BC∥AD,
∴∠1=∠2,
∵CF平分∠BCD,AE平分∠BAD,
∴∠1=∠4=∠BCD,∠3=∠BAD,
∴∠1=∠3,
∴∠2=∠3,
∴AE∥CF,
∴四边形AHCF是平行四边形;
(2)证明:∵四边形AHCF是平行四边形,
∴AF=CH,
∵AE∥CF,
∴∠E=∠4,∠5=∠1,
∴∠E=∠5,
∴CH=EC,
∴AF=EC;
(3)解:△BEG是等腰直角三角形;理由如下:
连接AG,过G作GN∥BC交AB于N,如图2所示:
∵四边形ABCD是平行四边形,∠BAD=90°,
∴四边形ABCD是矩形,
∴BC∥AD,∠CBN=90°,
∴∠GNB=90°,BC∥GN∥AD,
∵G为CF的中点,
∴N为AB中点,
即NG是AB的垂直平分线,
∴BG=AG,
∴∠BGN=∠AGN,
∵NG∥AD,
∴∠AGN=∠GAF=∠BGN,
∵CF平分∠BCD,∠BCD=90°,
∴∠DCF=90°,∠DCF=45°,
∴∠DFC=45°,
∴∠ECG=∠AFC=90°+45°=135°,
在△AFG和△ECG中,
,
∴△AFG≌△ECG(SAS),
∴AG=EG=BG,∠EGC=∠AGF,∠GAF=∠GEC,
∵∠AGN=∠GAF=∠BGN,
∴∠AGN=∠GAF=∠BGN=∠GEC,
∵∠GAF+∠AGF=180°-135°=45°,
∴∠EGC+∠BGF=2(∠GAF+∠AGF)=90°,
即∠BGE=90°,
∴△BEG是等腰直角三角形;
(4)作GM⊥AD于M,如图2所示:
则GM∥CD,
∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,CD=AB=6,AD=BC=7,
∴∠DCF=45°,
∴∠DFC=45°,
∴△DCF、△MGF是等腰直角三角形,
∴FD=CD=6,GM=FM,
∵G为CF的中点,
∴GM为△DCF的中位线,
∴FM=GM═DM=CD=3,
∴AM=7-3=4,
∴AG=,
∴BG=EG=5,
∴△BEG的面积=BG EG=.
85.(1)见解析;(2)
【分析】
(1)连接交于点,根据平行四边形的性质可以判定OF为△DBE的中位线,即可证明;
(2)根据AD=2,∠ACD=90°,∠ADC=60°,可求出AC的长,再根据中位线的性质即可求解;
【详解】
解:(1)连接交于点,
∵四边形是平行四边形,
∴,
∵,
∴OF为△DBE的中位线
∴.
(2)∵AD=2,∠ACD=90°,∠ADC=60°,
∴.
∵是的中位线,
∴.
∴.
∵,
∴.
【点睛】
本题考查了三角形中位线的性质以及平行四边形的性质,正确掌握知识点是解题的关键;
86.(1)见解析;(2)2
【分析】
(1)利用中位线性质可得,.,.可证四边形是平行四边形.由平行四边形性质可得,.
(2)由和,可推得.求由点是中点,.由三等分可求.根据平行四边形性质可得四边形的面积.
【详解】
(1)证明:∵点,分别是,的中点,
∴,.
∵点,分别是,的中点,
∴,.
∴,.
∴四边形是平行四边形.
∴,;
(2)解:∵,
∴.
又∵,
∴.
∵,,
∵,
∵点是中点,
∴.
∴.
∴四边形的面积.
【点睛】
本题考查中位线性质,平行四边形的判定与性质,中线的性质,掌握中位线性质,平行四边形的判定与性质,中线的性质,注意中线与中位线的区别以及它们性质是解题关键.
87.证明:在ABCD中,AD=BC且AD∥BC,
∵BE=FD,∴AF=CE.
∴四边形AECF是平行四边形
【详解】
试题分析:根据平行四边形的性质可得AF∥EC.AF=EC,然后根据平行四边形的定义即可证得.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E,F分别是BC,AD的中点,
∴,,
∴AF∥EC,AF=EC,
∴四边形AECF是平行四边形.
【点评】本题考查了平行四边形的性质与判定;熟练掌握平行四边形的性质,证出AF=EC是解决问题的关键.
88.(1)证明见解析;(2),证明见解析;(3)=3.
【分析】
(1)证明△AGE≌△ACE,根据全等三角形的性质可得到GE=EC,再利用三角形的中位线定理证明DE∥AB,再加上条件EF∥BC可证出结论;
(2)先证明BF=DE=BG,再证明AG=AC,可得到BF=(AB AG)=(AB AC);
(3) 根据△DCE中DC边上的高与BDEF中BD边上的高相等,得出BDEF的面积为6,设BDEF中BF边上的高为h,由即可求解.
【详解】
(1)延长交于点,
,,
又∵平分,
∴∠GAE=∠CAE
在和中,,
,
,
∵点是边的中点,
∴
为的中位线,
,
,
四边形是平行四边形.
(2)四边形是平行四边形,
,
,分别是,的中点,
,
,
,
.
(3)如图:
∵BD=DC,EF∥BC
∴△DCE中DC边上的高与BDEF中BD边上的高相等,
∴
∵BF∥DE
设BDEF中BF边上的高为h,
则
=(DE+BP)×h÷2-BP×h÷2
=DE×h÷2
=6÷2
=3.
【点睛】
此题主要考查了平行四边形的判定与性质,全等三角形的判定与性质,三角形中位线定理,以及等底同高的平行四边形和三角形的面积之间的关系,证明GE=EC,再利用三角形中位线定理证明DE∥AB是解决问题的关键.
答案第1页,共2页
一、单选题
1.(2021·山东鄄城·八年级期末)如图, ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A.15 B.18 C.21 D.24
2.(2021·山东莱阳·八年级期末)小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,② B.①,④ C.③,④ D.②,③
3.(2021·山东·东平县实验中学八年级期末)已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE=DC B.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
4.(2021·山东冠县·八年级期末)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
5.(2021·山东蒙阴·八年级期末)如图,P是面积为S的内任意一点,的面积为,的面积为,则( )
A. B.
C. D.的大小与P点位置有关
6.(2021·山东诸城·八年级期末)如图,在平行四边形中,平分,则平行四边形的周长是( )
A. B. C. D.
7.(2021·山东·东平县实验中学八年级期末)如图,在平行四边形ABCD中,,的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,,垂足为G,若,则AE的边长为
A. B. C.4 D.8
8.(2021·山东河口·八年级期末)如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
A. B.2 C. D.3
9.(2021·山东泰山·八年级期末)如图,在中,,是的中点,过点作的平行线,交于点E,作的垂线交于点,若,且的面积为1,则的长为( )
A. B.5 C. D.10
10.(2021·山东台儿庄·八年级期末)已知的周长为16,点,,分别为三条边的中点,则的周长为( )
A.8 B. C.16 D.4
11.(2021·山东莒南·八年级期末)如图,是边延长线上一点,连接,,,交于点.添加以下条件,不能判定四边形为平行四边形的是( )
A. B.
C. D.
12.(2021·山东郓城·八年级期末)如图,在四边形中,是边的中点,连接并延长,交的延长线于点,.添加一个条件使四边形是平行四边形,你认为下面四个条件中可选择的是( )
A. B. C. D.
13.(2021·山东台儿庄·八年级期末)如图,在四边形ABCD中,AC与BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AB=DC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
14.(2021·山东莱阳·八年级期末)如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
15.(2021·山东河口·八年级期末)如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=5.正确的个数是( )
A.1个 B.2个
C.3个 D.4个
16.(2021·山东·夏津县教学工作研究室八年级期末)如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4
C.5 D.6
17.(2021·山东蒙阴·八年级期末)如图,将矩形折叠,使点和点重合,折痕为,与交于点若,,则的长为( )
A. B. C. D.
18.(2021·山东兖州·八年级期末)如图,将一个边长为4和8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
A. B. C. D.
19.(2021·山东·淄博市临淄区教学研究室八年级期末)如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
A. B.2 C. D.6
20.(2021·山东福山·八年级期末)如图,点是矩形的对角线上一点,过点作,分别交于,连接,若,则图中阴影部分的面积为( )
A. B.
C. D.
21.(2021·山东文登·八年级期末)矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,连接AG,取AG的中点H,连接EH.若,,则( )
A. B.2 C. D.
22.(2021·山东台儿庄·八年级期末)如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则DE的长为( )
A. B. C. D.
23.(2021·山东博兴·八年级期末)如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2,则AC的长为( )
A.2 B.4 C.6 D.8
24.(2021·山东武城·八年级期末)如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.2 B.3 C.5 D.6
25.(2021·山东陵城·八年级期末)如图,在平面直角坐标系中,四边形为菱形,,,,则对角线交点的坐标为( )
A. B. C. D.
26.(2021·山东福山·八年级期末)如图,菱形中,E,F分别是,的中点,若,则菱形的周长为( )
A.20 B.30 C.40 D.50
27.(2021·山东中区·八年级期末)如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )
A.1个 B.2个 C.3个 D.4个
28.(2021·山东金乡·八年级期末)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A. B. C.12 D.24
29.(2021·山东临淄·八年级期末)如图,菱形的边长为13,对角线,点E、F分别是边、的中点,连接并延长与的延长线相交于点G,则( )
A.13 B.10 C.12 D.5
30.(2021·山东中区·八年级期末)矩形具有而菱形不具有的性质是( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
31.(2021·山东安丘·八年级期末)如图,已知线段AB,分别以A,B为圆心,大于同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是( )
A.AB平分∠CAD B.CD平分∠ACB C.AB⊥CD D.AB=CD
32.(2021·山东槐荫·八年级期末)若顺次连接四边形ABCD各边的中点所得四边形是菱形.则四边形ABCD一定是 ( )
A.菱形 B.对角线互相垂直的四边形
C.矩形 D.对角线相等的四边形
33.(2021·山东临邑·八年级期末)如图,正方形的边长为4,点在上且,为对角线上一动点,则周长的最小值为( ).
A.5 B.6 C.7 D.8
34.(2021·山东阳信·八年级期末)如图,在长方形中无重叠放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( )
A. B. C. D.
35.(2021·山东东平·八年级期末)平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
36.(2021·山东禹城·八年级期末)如图,点O(0,0),A(0,1)是正方形的两个顶点,以对角线为边作正方形,再以正方形的对角线作正方形,…,依此规律,则点的坐标是( )
A.(-8,0) B.(0,8)
C.(0,8) D.(0,16)
37.(2021·山东蒙阴·八年级期末)下列命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相垂直且平分的四边形是菱形;
③一个角为90°且一组邻边相等的四边形是正方形;
④对角线相等的平行四边形是矩形.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
38.(2021·山东临淄·八年级期末)下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
39.(2021·山东福山·八年级期末)如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )
A.()n﹣1 B.2n﹣1 C.()n D.2n
二、填空题
40.(2021·山东莱州·八年级期末)如图,在 ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为__________.
41.(2021·山东滕州·八年级期末)如图,在中,过点C作,垂足为E,若,则的度数为____.
42.(2021·山东招远·八年级期末)如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=8,EF=1,则BC长为__________.
43.(2021·山东槐荫·八年级期末)如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连结OE.下列结论:
①∠CAD=30°;②S ABCD=AB·AC;③OB=AB;④OE=BC,成立的结论有______.(填序号)
44.(2021·山东莱州·八年级期末)如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
45.(2021·山东中区·八年级期末)如图,点的坐标为,点在轴上,把沿轴向右平移到,若四边形的面积为9,则点的坐标为_______.
46.(2021·山东台儿庄·八年级期末)如图,在平行四边形中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为______.
47.(2021·山东河口·八年级期末)如图,在平行四边形中,点为边上一点,,点,点分别是中点,若,则的长为__________.
48.(2021·山东滨州·八年级期末)如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件____,使四边形ABCD是平行四边形(填一个即可).
49.(2021·山东莱州·八年级期末)如图,平行四边形ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,连接AP,若S△PBG=2,则S四边形AEPH=_____.
50.(2021·山东桓台·八年级期末)如图,在矩形ABCD中,,,点E在边BC上,且.连接AE,将沿AE折叠,若点B的对应点落在矩形ABCD的边上,则 a的值为________.
51.(2021·山东蒙阴·八年级期末)如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是_____.
52.(2021·山东周村·八年级期末)如图,有一张长方形片ABCD,,.点E为CD上一点,将纸片沿AE折叠,BC的对应边恰好经过点D,则线段DE的长为________cm.
53.(2021·山东台儿庄·八年级期末)如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为_____.
54.(2021·山东沂源·八年级期末)如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=_____cm.
55.(2021·山东单县·八年级期末)如图,在菱形中,,点在上,若,则__________.
56.(2021·山东肥城·八年级期末)如图,在菱形中,对角线交于点,过点作于点,已知BO=4,S菱形ABCD=24,则___.
57.(2021·山东安丘·八年级期末)如图,将两张对边平行且相等的纸条交叉叠放在一起,则重合部分构成的四边形ABCD_________菱形(是,或不是).
58.(2021·山东蓬莱·八年级期末)如图,在菱形中,对角线相交于点O,点E在线段BO上,连接AE,若,,,则线段AE的长为_____.
59.(2021·山东泗水·八年级期末)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是___.
60.(2021·山东安丘·八年级期末)用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为____________(用含a,b的代数式表示).
61.(2021·山东莱州·八年级期末)如图,正方形的边长为4,点在上且,为对角线上一动点,则周长的最小值为_____________.
62.(2021·山东平阴·八年级期末)如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF.下列结论:①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP.其中正确的结论是__.(请填序号)
63.(2021·山东·日照市新营中学八年级期末)如图,在菱形ABCD中,,且,点F为对角线AC的动点,点E为AB上的动点,则的最小值为______.
64.(2021·山东文登·八年级期末)如图,在中,,,点D是AB上一动点,以AC为对角线的所有平行四边形ADCE中,DE的最小值是________.
三、解答题
65.(2021·山东长清·八年级期末)如图,在 ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.
66.(2021·山东罗庄·八年级期末)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连接DF
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
67.(2021·山东临淄·八年级期末)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
68.(2021·山东定陶·八年级期末)在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
69.(2021·山东郓城·八年级期末)如图,已知△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,EF=DC.
(1)求证:四边形EFCD是平行四边形.
(2)若BE=EF,求证:AE=AD.
70.(2021·山东福山·八年级期末)如图,在平行四边形中,对角线与交于点O,点M,N分别为、的中点,延长至点E,使,连接.
(1)求证:;
(2)若,且,,求四边形的面积.
71.(2021·山东崂山·八年级期末)如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数;
(2)如果AD=5cm,AP=8cm,求△APB的周长.
72.(2021·山东·东平县实验中学八年级期末)如图,在 ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
73.(2021·山东济南·八年级期末)已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF
求证:四边形BECF是平行四边形.
74.(2021·山东蓬莱·八年级期末)如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断 ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
75.(2021·山东鄄城·八年级期末)如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.
76.(2021·山东台儿庄·八年级期末)如图,点在一条直线上,.
(1)求证:;
(2)连接,求证:四边形是平行四边形.
77.(2021·山东博兴·八年级期末)如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
78.(2021·山东周村·八年级期末)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作,,垂足分别为E,F.AC平分.
(1)若,求的度数;
(2)求证:.
79.(2021·山东莱阳·八年级期末)如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD.
(1)求证:四边形ABCD是平行四边形;
(2)如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
80.(2021·山东金乡·八年级期末)如图,在 中,,过点 的直线MN//AB,为 边上一点,过点 作 ,垂足为点 ,交直线 于点 ,连接 ,.
(1)求证:;
(2)当 为 中点时,四边形 是什么特殊四边形 说明你的理由;
(3)在()的条件下,当 的大小满足什么条件时,四边形 是正方形 请说明你的理由.
81.(2021·山东莱芜·八年级期末)如图,在中,对角线与相交于点,点,分别在和的延长线上,且,连接,.
(1)求证:≌;
(2)连接,,当平分时,四边形是什么特殊四边形?请说明理由.
82.(2021·山东招远·八年级期末)如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
83.(2021·山东广饶·八年级期末)如图.在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形.
(2)若连接DE,交AC于点F,试判断四边形ABDE的形状(直接写出结果,不需要证明).
(3)△ABC再添加一个什么条件时,可使四边形ADCE是正方形.并证明你的结论.
84.(2021·山东德城·八年级期末)如图,在□ABCD中,∠BCD的平分线交直线AD于点F,∠BAD的平分线交DC延长线于E,交线段BC于H点
(1)证明:四边形AHCF是平行四边形;
(2)证明:AF=EC;
(3)若∠BAD=90°,G为CF的中点(如右图),判断△BEG的形状,并证明;
(4)在(3)的条件上,若已知AB=6,BC=7,试求△BEG的面积.
85.(2021·山东乳山·八年级期末)如图,点在外,连接,,延长交于,为的中点.
(1)求证:;
(2)若,,,,求的长.
86.(2021·山东周村·八年级期末)如图,在中,,中线,相交于点,点,分别为,的中点.
(1)求证:,;
(2)若,,求四边形的面积.
87.(2021·山东天桥·八年级期末)如图,在ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
88.(2021·山东张店·八年级期末)如图1,在中,点是边的中点,点在内,平分,,点在边上,.
(1)求证:四边形是平行四边形.
(2)判断线段、、的数量之间具有怎样的关系?证明你所得到的结论.
(3)点是的边上的一点,若的面积,请直接写出的面积(不需要写出解答过程).
试卷第1页,共3页
参考答案:
1.A
【分析】
此题涉及的知识点是平行四边形的性质.根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
【详解】
解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,DE=CD,
∴OE是△BCD的中位线,∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故选A
【点睛】
此题重点考察学生对于平行四边形的性质的理解,三角形的中位线,平行四边形的对角对边性质是解题的关键.
2.D
【分析】
确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
【详解】
只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
【点睛】
本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.
3.D
【详解】
由平行四边形的性质和三角形中位线定理得出选项A、B、C正确;由OB≠OC,得出∠OBE≠∠OCE,选项D错误;即可得出结论.
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB∥DC,
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE=DC,OE∥DC,
∴OE∥AB,
∴∠BOE=∠OBA,
∴选项A、B、C正确;
∵OB≠OC,
∴∠OBE≠∠OCE,
∴选项D错误;
故选D.
“点睛”此题考查了平行四边形的性质,还考查了三角形中位线定理,解决问题的方法是采用排除法解答.
4.B
【分析】
直接利用平行四边形的性质得出AO=CO,BO=DO,DC=AB=6,再利用已知求出AO+BO的长,进而得出答案.
【详解】
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,DC=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长是:14.
故选B.
【点睛】
平行四边形的性质掌握要熟练,找到等值代换即可求解.
5.C
【分析】
过点P作AD的垂线PF,交AD于F,再延长FP交BC于点E,表示出S1+ S2,得到即可.
【详解】
解:如图,过点P作AD的垂线PF,交AD于F,再延长FP交BC于点E,
根据平行四边形的性质可知PE⊥BC,AD=BC,
∴S1=AD×PF,S2=BC×PE,
∴S1+ S2
=AD×PF+BC×PE
=AD×(PE+PE)
=AD×EF
=S,
故选C.
【点睛】
本题考查了三角形的面积和平行四边形的性质,解题的关键是作出平行四边形过点P的高.
6.C
【分析】
根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出 ABCD的周长.
【详解】
解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,BC=AD=6,AB=CD,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵AD=6,BE=2,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴ ABCD的周长=6+6+4+4=20.
故选:C.
【点睛】
本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,熟练掌握平行四边形的性质,证明CE=CD是解题的关键.
7.B
【分析】
由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF与三角形ECF全等,得出AF=EF,即可求出AE的长.
【详解】
∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB,
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,又F为DC的中点,
∴DF=CF,
∴AD=DF=DC=AB=2,
在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,
∵平行四边形ABCD,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=4.
故选B.
考点:1.平行四边形的性质;2.等腰三角形的判定与性质;3.勾股定理.
8.C
【分析】
证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.
【详解】
解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
,
∴△BNA≌△BNE,
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19-BC=19-7=12,
∴DE=BE+CD-BC=5,
∴MN=DE=.
故选C.
【点睛】
本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
9.A
【分析】
过A作AH⊥BC于H,根据已知条件得到AE=CE,求得DE=BC,求得DF=AH,根据三角形的面积公式得到DE DF=2,得到AB AC=8,求得AB=2(负值舍去),根据勾股定理即可得到结论.
【详解】
解:过A作AH⊥BC于H,
∵D是AB的中点,
∴AD=BD,
∵DE∥BC,
∴AE=CE,
∴DE=BC,
∵DF⊥BC,
∴DF∥AH,DF⊥DE,
∴BF=HF,
∴DF=AH,
∵△DFE的面积为1,
∴DE DF=1,
∴DE DF=2,
∴BC AH=2DE 2DF=4×2=8,
∴AB AC=8,
∵AB=CE,
∴AB=AE=CE=AC,
∴AB 2AB=8,
∴AB=2(负值舍去),
∴AC=4,
∴BC=.
故选:A.
【点睛】
本题考查了三角形中位线定理,三角形的面积的计算,勾股定理,平行线的判定和性质,正确的识别图形是解题的关键.
10.A
【分析】
由,,分别为三条边的中点,可知DE、EF、DF为的中位线,即可得到的周长.
【详解】
解:如图,
∵,,分别为三条边的中点,
∴,,,
∵,
∴,
故选:A.
【点睛】
本题考查了三角形的中位线,熟练掌握三角形的中位线平行于第三边且是第三边的一半是解题的关键.
11.C
【分析】
根据平行四边形的性质得到AD∥BC,AB∥CD,求得DE∥BC,∠ABD=∠CDB,推出BD∥CE,于是得到四边形BCED为平行四边形,故A正确;根据平行线的性质得到∠DEF=∠CBF,根据全等三角形的性质得到EF=BF,于是得到四边形BCED为平行四边形,故B正确;根据平行线的性质得到∠AEB=∠CBF,求得∠CBF=∠BCD,求得CF=BF,同理,EF=DF,不能判定四边形BCED为平行四边形;故C错误;根据平行线的性质得到∠DEC+∠BCE=∠EDB+∠DBC=180°,推出∠BDE=∠BCE,于是得到四边形BCED为平行四边形,故D正确.
【详解】
∵四边形是平行四边形,
∴,,
∴,,
∵,
∴,
∴,
∴为平行四边形,故A正确;
∵,
∴,
在与中,
,
∴,
∴,
∵,
∴四边形为平行四边形,故B正确;
∵,
∴,
∵,
∴,
∴,
同理,,
∴不能判定四边形为平行四边形;故C错误;
∵,
∴,
∵,
∴,
∴四边形为平行四边形,故D正确,
故选C.
【点睛】
本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.
12.D
【分析】
把A、B、C、D四个选项分别作为添加条件进行验证,D为正确选项.添加D选项,即可证明△DEC≌△FEB,从而进一步证明DC=BF=AB,且DC∥AB.
【详解】
添加A、,无法得到AD∥BC或CD=BA,故错误;
添加B、,无法得到CD∥BA或,故错误;
添加C、,无法得到,故错误;
添加D、
∵,,,
∴,,∴,
∵,∴,
∴四边形是平行四边形.
故选D.
【点睛】
本题是一道探索性的试题,考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
13.C
【分析】
根据平行四边形的判定方法逐项分析即可.
【详解】
A. ∵ AB∥DC,AB=DC,∴四边形ABCD是平行四边形;
B. ∵ AB=DC,AD=BC,∴四边形ABCD是平行四边形;
C.等腰梯形ABCD满足 AB∥DC,AD=BC,但四边形ABCD是平行四边形;
D. OA=OC,OB=OD,∴四边形ABCD是平行四边形;
故选C.
【点睛】
本题主要考查了平行四边形的判定,平行四边形的判定方法有:①两组对边分别平行的四边形是平行四边形;②一组对边平行且相等的四边形是平行四边形;③两组对边分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤.两组对角分别相等的四边形是平行四边形.
14.A
【分析】
根据平行线的性质得到∠AEB=∠CBF,求得∠CBF=∠BCD,求得CF=BF,同理,EF=DF,不能判定四边形BCED为平行四边形;故A错误;根据平行线的性质得到∠DEF=∠CBF,根据全等三角形的性质得到DF=CF,于是得到四边形BCED为平行四边形,故B正确;根据平行四边形的性质得到AD∥BC,AB∥CD,求得DE∥BC,∠ABD=∠CDB,推出BD∥CE,于是得到四边形BCED为平行四边形,故C正确;根据平行线的性质得到∠DEC+∠BCE=∠EDB+∠DBC=180°,推出∠BDE=∠BCE,于是得到四边形BCED为平行四边形,故D正确.
【详解】
解:A、∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故A错误;
∵ DE∥BC,
∴∠DEF=∠CBF,
∠DEF=∠CBF
在△DEF与△CBF中,
∴△DEF△CBF(ASA),
∴DF=CF
∵EF=BF
∴四边形BCED为平行四边形,故B正确;
∵四边形ABCD是平行四边形,
∴ .AD∥BC,AB∥CD,
∴DE∥CE,∠ABD=∠CDB,
∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故C正确;
∵AEB∥C,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确.
故选:A.
【点睛】
本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.
15.C
【分析】
由,得出∠BAC=90°,则①正确;由等边三角形的性质得∠DAB=∠EAC=60°,则∠DAE=150°,由SAS证得△ABC≌△DBF,得AC=DF=AE=4,同理△ABC≌△EFC(SAS),得AB=EF=AD=3,得出四边形AEFD是平行四边形,则②正确;由平行四边形的性质得∠DFE=∠DAE=150°,则③正确;∠FDA=180°-∠DFE=30°,过点作于点,,则④不正确;即可得出结果.
【详解】
解:∵,
∴,
∴∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
又∴∠BAC=90°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
∴∠FDA=180°-∠DFE=180°-150°=30°,
过点作于点,
∴,
故④不正确;
∴正确的个数是3个,
故选:C.
【点睛】
本题考查了平行四边形的判定与性质、勾股定理的逆定理、全等三角形的判定与性质、等边三角形的性质、平角、周角、平行是四边形面积的计算等知识;熟练掌握平行四边形的判定与性质是解题的关键.
16.D
【详解】
试题分析:先根据矩形的特点求出BC的长,再由翻折变换的性质得出△CEF是直角三角形,利用勾股定理即可求出CF的长,再在△ABC中利用勾股定理即可求出AB的长.
解:∵四边形ABCD是矩形,AD=8,
∴BC=8,
∵△AEF是△AEB翻折而成,
∴BE=EF=3,AB=AF,△CEF是直角三角形,
∴CE=8﹣3=5,
在Rt△CEF中,CF===4,
设AB=x,
在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,
故选D.
考点:翻折变换(折叠问题);勾股定理.
17.C
【分析】
先证明再求解利用轴对称可得答案.
【详解】
解:由对折可得:
矩形,
BC=8
由对折得:
故选C.
【点睛】
本题考查的是矩形的性质,等腰三角形的判定,勾股定理的应用,轴对称的性质,掌握以上知识是解题的关键.
18.D
【详解】
根据折叠的性质知,四边形AFEB与四边形FDCE全等,有EC=AF=AE,
由勾股定理得,AB2+BE2=AE2即42+(8﹣AE)2=AE2,解得,AE=AF=5,BE=3,
作EG⊥AF于点G,则四边形AGEB是矩形,有AG=3,GF=2,GE=AB=4,由勾股定理得EF=.
故选D.
19.B
【分析】
先由题意得到大正方形的边长和小正方形的边长,再求阴影部分的面积.
【详解】
由题意可得,大正方形的边长为,小正方形的边长为,
∴图中阴影部分的面积为:,故选B.
【点睛】
本题考查矩形面积的求法,解题的关键是得到大正方形的边长和小正方形的边长.
20.A
【分析】
先根据矩形的性质证得,然后求解即可.
【详解】
解:作PM⊥AD于M,交BC于N,
∴四边形AEPM、四边形DFPM、四边形CFPN和四边形BEPN都是矩形,
∵,,,,,
∴S矩形DFPM=S矩形BEPN,
∵PM=AE=1,PF=NC=3,
∴,
∴S阴=,
故选:A.
【点睛】
本题主要考查矩形的性质、三角形的面积等知识,证得是解答本题的关键.
21.A
【分析】
延长GE交AB于点R,连接AE,设AG交DE于点M,过点E作EN⊥AG于N,先计算出RG=6,∠ARG=,AR=2,根据勾股定理求出,得到HG=,利用,求出,即可利用勾股定理求出NG、EH.
【详解】
如图,延长GE交AB于点R,连接AE,设AG交DE于点M,过点E作EN⊥AG于N,
∵矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,
∴RG=BF=BC+CF=2+4=6,∠ARG=,AR=AR-CE=4-2=2,
∴,
∵H是AG中点,
∴HG=,
∵,
∴,
∴,
在Rt△ENG中, ,
∴,
∴,
故选:A.
【点睛】
此题考查矩形的性质,勾股定理,线段中点的性质,三角形面积法求线段长度,熟记矩形的性质及熟练运用勾股定理是解题的关键.
22.B
【分析】
先根据矩形的性质得AD=BC=5,AB=CD=3,再根据折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=4,则CF=BC﹣BF=1,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理得到x2+12=(3﹣x)2,解方程即可得到DE的长.
【详解】
解:∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
在Rt△ABF中,BF===4,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则DE=EF=3﹣x,
在Rt△ECF中,CE2+FC2=EF2,
∴x2+12=(3﹣x)2,
解得x=,
∴DE=3﹣x=,
故选:B.
【点睛】
本题考查了翻折变换、矩形的性质、勾股定理等知识,属于常考题型,灵活运用这些性质进行推理与计算是解题的关键.
23.B
【分析】
已知四边形ABCD是矩形,∠AOD=120°,AB=2,根据矩形的性质可证得△AOB是等边三角形,则OA=OB=AB=2,AC=2OA=4.
【详解】
∵四边形ABCD是矩形
∴AC=BD,OA=OC,OB=OD
∴OA=OB
∵∠AOD=120°
∴∠AOB=60°
∴△AOB是等边三角形
∴OA=OB=AB=2
∴AC=2OA=4
故选:B
【点睛】
本题考查了矩形的基本性质,等边三角形的判定和性质.
24.C
【详解】
试题分析:连接EF交AC于点M,由四边形EGFH为菱形可得FM=EM,EF⊥AC;利用”AAS或ASA”易证△FMC≌△EMA,根据全等三角形的性质可得AM=MC;在Rt△ABC中,由勾股定理求得AC=,且tan∠BAC=;在Rt△AME中,AM=AC= ,tan∠BAC=可得EM=;在Rt△AME中,由勾股定理求得AE=5.故答案选C.
考点:菱形的性质;矩形的性质;勾股定理;锐角三角函数.
25.D
【分析】
过点作轴于点,由直角三角形的性质求出长和长即可.
【详解】
解:过点作轴于点,
∵四边形为菱形,,
∴,OB⊥AC,,
∵,∴,
∴,
∴,,
∴,
∴.
故选D.
【点睛】
本题考查了菱形的性质、勾股定理及含30°直角三角形的性质,正确作出辅助线是解题的关键.
26.C
【分析】
由题意可知EF为△ABD的中位线,可求出AB的长,由于菱形四条边相等即可得到周长.
【详解】
解:∵E,F分别是,的中点,
∴EF为△ABD的中位线,
∴,
∵四边形是菱形,
∴,
∴菱形的周长为
故选:C.
【点睛】
本题考查了三角形的中位线,菱形的性质,发现EF为△ABD的中位线是解题的关键.
27.C
【分析】
由折叠的性质可得四边形EBFG是菱形从而判断①②正确;由角平分线定理即可判断DG≠GH,由此推出③错误;根据F、C重合时的性质,可得∠AEB=30°,进而算出④正确.
【详解】
连接BE,由折叠可知BO=GO,
∵EG//BF,
∴∠EGO=∠FBO,
又∵∠EOG=∠FOB,
∴△EOG≌△FOB(ASA) ,
∴EG=BF,
∴四边形EBFG是平行四边形,
由折叠可知BE=EG,
则四边形EBFG为菱形,
故EF⊥BG,GE=GF,
∴①②正确;
∵四边形EBFG为菱形,
∴KG平分∠DGH,
∴,DG≠GH,
∴ S△GDK≠S△GKH,故③错误;
当点F与点C重合时,BE=BF=BC=12=2AB,
∴∠AEB=30°,,故④正确.
综合,正确的为①②④.
故选C.
【点睛】
本题考查矩形的性质,菱形的判断,折叠的性质,关键在于结合图形对线段和角度进行转换.
28.A
【详解】
解:如图,设对角线相交于点O,
∵AC=8,DB=6,∴AO=AC=×8=4,BO=BD=×6=3,
由勾股定理的,AB===5,
∵DH⊥AB,∴S菱形ABCD=AB DH=AC BD,
即5DH=×8×6,解得DH=.
故选A.
【点睛】
本题考查菱形的性质.
29.B
【分析】
连接对角线BD,交AC于点O,求证四边形BDEG是平行四边形,EG=BD,利用勾股定理求出OD的长,BD=2OD,即可求出EG.
【详解】
连接BD,交AC于点O,
由题意知:菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB=BC=CD=DA=13, EFBD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵ABCD,EFBD
∴DEBG,BDEG
在四边形BDEG中,
∵DEBG,BDEG
∴四边形BDEG是平行四边形
∴BD=EG
在△COD中,
∵OC⊥OD,CD=13,CO=12
∴OD=OB=5
∴BD=EG=10
故选B.
【点睛】
本题主要考查了菱形的性质,平行四边形的性质及勾股定理,熟练掌握菱形、平行四边形的性质和勾股定理是解题的关键.
30.A
【详解】
解:菱形的对角线互相平分、垂直、对角线平分一组对角,
矩形的对角线互相平分、相等,
∴矩形具有而菱形不具有的性质是对角线相等,
故选A.
考点:1.菱形的性质;2.矩形的性质.
31.D
【分析】
根据作图判断出四边形ACBD是菱形,再根据菱形的性质:菱形的对角线平分一组对角、菱形的对角线互相垂直平分可得出答案
【详解】
解:由作图知AC=AD=BC=BD,
∴四边形ACBD是菱形,
∴AB平分∠CAD、CD平分∠ACB、AB⊥CD,
不能判断AB=CD,
故选:D.
【点睛】
本题主要考查线段垂直平分线的尺规作图、菱形的判定方法等,解题的关键是掌握菱形的判定与性质.
32.D
【分析】
根据三角形的中位线定理得到EH∥FG,EF=FG,EF=BD,要是四边形为菱形,得出EF=EH,即可得到答案.
【详解】
解:∵E,F,G,H分别是边AD,DC,CB,AB的中点,
∴EH=AC,EH∥AC,FG=AC,FG∥AC,EF=BD,
∴EH∥FG,EF=FG,
∴四边形EFGH是平行四边形,
假设AC=BD,
∵EH=AC,EF=BD,
则EF=EH,
∴平行四边形EFGH是菱形,
即只有具备AC=BD即可推出四边形是菱形,
故选D.
33.B
【分析】
连接ED交AC于一点F,连接BF,根据正方形的对称性得到此时的周长最小,利用勾股定理求出DE即可得到答案.
【详解】
连接ED交AC于一点F,连接BF,
∵四边形ABCD是正方形,
∴点B与点D关于AC对称,
∴BF=DF,
∴的周长=BF+EF+BE=DE+BE,此时周长最小,
∵正方形的边长为4,
∴AD=AB=4,∠DAB=90°,
∵点在上且,
∴AE=3,
∴DE=,
∴的周长=5+1=6,
故选:B.
【点睛】
此题考查正方形的性质:四条边都相等,四个角都是直角以及正方形的对称性质,还考查了勾股定理的计算,依据对称性得到连接DE交AC于点F是的周长有最小值的思路是解题的关键.
34.B
【分析】
先根据正方形的面积公式求出两张正方形纸片的边长,从而可得长方形ABCD的长与宽,再利用长方形ABCD的面积减去两个正方形的面积即可得.
【详解】
面积为的正方形纸片的边长为,
则,
面积为的正方形纸片的边长为,
则,
因此,图中空白部分面积为,
故选:B.
【点睛】
本题考查了二次根式的几何应用,正确求出两个正方形的边长是解题关键.
35.A
【详解】
试题分析:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选A.
考点:特殊四边形的性质
36.D
【分析】
根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以,可求出从A到A3变化后的坐标,再求出A1、A2、A3、A4、A5,继而得出A8坐标即可.
【详解】
解:根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘,
∵从A到经过了3次变化,
∵45°×3=135°,1×=2,
∴点所在的正方形的边长为2,点位置在第四象限,
∴点的坐标是(2,-2),
可得出:点坐标为(1,1),
点坐标为(0,2),点坐标为(2,-2),
点坐标为(0,-4),点坐标为(-4,-4),
(-8,0),A7(-8,8),(0,16),
故选D.
【点睛】
本题考查了规律题,点的坐标,观察出每一次的变化特征是解答本题的关键.
37.B
【分析】
根据平行四边形的判定,菱形的判定,正方形的判定,矩形的判定逐一判断即可.
【详解】
解:①一组对边平行,另一组对边相等的四边形是平行四边形,是假命题;
②对角线互相垂直且平分的四边形是菱形,是真命题;
③一个角为90°且一组邻边相等的四边形是正方形,是假命题;
④对角线相等的平行四边形是矩形,是真命题.
故选:B.
【点睛】
本题考查了平行四边形、菱形、正方形、矩形的判定,熟知特殊四边形的判定定理是解题关键.
38.B
【分析】
利用平行四边形的判定、菱形的判定、矩形的判定及正方形的判定定理对各选项逐一判断后即可确定正确的选项.
【详解】
解:A、一组对边平行,另一组对边相等的四边形是平行四边形错误,如等腰梯形;
B、对角线互相垂直平分的四边形是菱形,正确;
C、对角线相等的四边形是矩形错误,如等腰梯形;
D、对角线互相垂直且相等的四边形是正方形错误,如一般四边形对角线也可以互相垂直且相等.
故选:B.
【点睛】
本题考查了命题与定理,解题的关键是了解平行四边形的判定、菱形的判定、矩形的判定及正方形的判定定理,难度一般.
39.B
【详解】
【分析】先求出第一个正方形面积、第二个正方形面积、第三个正方形面积,…探究规律后,即可解决问题.
【详解】第一个正方形的面积为1=20,
第二个正方形的面积为()2=2=21,
第三个正方形的边长为22,
…
第n个正方形的面积为2n﹣1,
故选B.
【点睛】本题考查了规律型:图形的变化类,正方形的性质,根据前后正方形边长之间的关系找到Sn的规律是解题的关键.
40.30°.
【详解】
∵四边形ABCD是平行四边形
∴AB∥DC,∠ABC=∠D
∴∠DAB+∠D=180°,
∵∠D=100°,
∴∠DAB=80°, ∠ABC=100°
又∵∠DAB的平分线交DC于点E
∴∠EAD=∠EAB=40°
∵AE=AB
∴∠ABE=(180°-40°)=70°
∴∠EBC=∠ABC-∠ABE=100°-70°=30°.
考点:1.角平分线的性质;2.平行四边形的性质.
41.50°
【分析】
由平行四边形的性质得出∠B=∠EAD=40°,由角的互余关系得出∠BCE=90°-∠B即可.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠EAD=40°,
∵CE⊥AB,
∴∠BCE=90°-∠B=50°;
故答案为:50°.
【点睛】
本题考查了平行四边形的性质和三角形的内角和;熟练掌握平行四边形的性质,求出∠B的度数是解决问题的关键.
42.15
【分析】
由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB=8,同理可得DE=DC=8,再由EF的长,即可求出BC的长.
【详解】
解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=8,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=8,
同理可证:DE=DC=8,
∵EF=AF+DE-AD=1,
即8+8-AD=1,
解得:AD=15;
故答案为:15.
【点睛】
本题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出AF=AB是解决问题的关键.
43.①②④
【分析】
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S ABCD=AB AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.
【详解】
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=BC,
∴AE=BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴S ABCD=AB AC,故②正确,
∵AB=BC,OB=BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE=AB,
∴OE=BC,故④正确.
故答案为①②④.
【点睛】
本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式,熟练掌握性质定理和判定定理是解题的关键.
44.14.5
【分析】
根据平行四边形的性质易证三角形全等,进而易得AE=CF,故四边形的周长=AD+CD+EF,根据已知求解即可.
【详解】
解:在平行四边形ABCD中,AD∥BC,AC与BD互相平分
∴AO=OC,∠DAC=∠ACB,∠AOE=∠COF
∴△AOE≌△COF
∴AE=CF,OF=OE=2.5
∴四边形的周长=CF+DE+CD+EF
=AE+DE+CD+EF
=AD+CD+EF
=×2
=14.5.
故答案为:14.5.
【点睛】
本题考查了平行四边形的性质以及三角形全等的证明,将所求线段转化为已知线段是解题的关键.
45.(4,3)
【分析】
过点A作AH⊥x轴于点H,得到AH=3,根据平移的性质证明四边形ABDC是平行四边形,得到AC=BD,根据平行四边形的面积是9得到,求出BD即可得到答案.
【详解】
过点A作AH⊥x轴于点H,
∵A(1,3),
∴AH=3,
由平移得AB∥CD,AB=CD,
∴四边形ABDC是平行四边形,
∴AC=BD,
∵,
∴BD=3,
∴AC=3,
∴C(4,3)
故答案为:(4,3).
【点睛】
此题考查平移的性质,平行四边形的判定及性质,直角坐标系中点到坐标轴的距离与点坐标的关系.
46.16
【分析】
根据平行线的性质和角平分线的性质,得到∠BEC=90°,然后利用勾股定理,即可求出答案.
【详解】
解:如图,在平行四边形中,
∴,AD=BC,AD∥BC,AB∥CD,
∴∠AEB=∠CBE,∠DEC=∠BCE,∠ABC+∠DCB=180°
∵BE、CE分别是∠ABC和∠DCB的角平分线,
∴∠ABE=∠CBE,∠DCE=∠BCE,
∴∠AEB=∠ABE,∠DEC =∠DCE,∠CBE+∠BCE=90°
∴AB=AE=2,DE=DC=2,∠BEC=90°,
∴AD=2+2=4,
∴BC=AD=4,
在Rt△BCE中,由勾股定理,得
;
故答案为:16.
【点睛】
本题考查了平行四边形的性质,勾股定理,平行线的性质,角平分线的性质,解题的关键是熟练掌握所学的性质,正确求出角之间的关系进行解题.
47.8
【分析】
先根据三角形中位线定理可得BC的长,再根据平行四边形的性质可得AD的长,然后根据即可得.
【详解】
点,点分别是中点
是的中位线
四边形ABCD是平行四边形
又
故答案为:8.
【点睛】
本题考查了三角形中位线定理、平行四边形的性质等知识点,熟记三角形中位线定理是解题关键.
48.AD=BC(答案不唯一)
【分析】
根据平行四边形的判定方法添加一个条件即可.
【详解】
解:根据一组对边平行且相等的四边形是平行四边形,可以添加条件AD=BC,
根据两组对边分别平行的四边形是平行四边形,可以添加条件AB∥DC,
本题只需添加一个即可,
故答案为:AD=BC(答案不唯一).
【点睛】
本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
49.8
【分析】
由题意根据平行四边形的判定和性质,进行面积的等量代换分析即可求解.
【详解】
解:∵EF∥BC,GH∥AB,
∴四边形HPFD、四边形PGCF、四边形BGPE是平行四边形,
∴,
∵S△PBG=2,
∴,
∵CG=2BG,
∴,
∵,
∴.
故答案为:8.
【点睛】
本题考查的是平行四边形的判定和性质,熟练掌握平行四边形的性质定理是解题的关键.
50.或
【分析】
分两种情况:①点落在AD边上,根据矩形与折叠的性质易得,即可求出a的值;②点落在CD边上,证明,根据相似三角形对应边成比例即可求出a的值.
【详解】
解:分两种情况:
①当点落在AD边上时,如图1.
四边形ABCD是矩形,
,
将沿AE折叠,点B的对应点落在AD边上,
,
,
,
;
②当点落在CD边上时,如图2.
∵四边形ABCD是矩形,
,.
将沿AE折叠,点B的对应点落在CD边上,
,,,
,.
在与中,
,
,
,即,
解得,(舍去).
综上,所求a的值为或.
故答案为或.
【点睛】
本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.
51.(-10,3)
【详解】
试题分析:根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE,设CE=x,则BE=8-x,然后根据折叠的性质,可得EF=8-x,根据勾股定理可得,解得x=3,则OF=6,所以OC=10,由此可得点E的坐标为(-10,3).
故答案为:(-10,3)
52.5
【分析】
根据折叠的性质得到线段和角相等,然后在Rt△中,由勾股定理求出的长,则可得出的长,再在Rt△利用勾股定理进行计算即可求DE的长.
【详解】
解:∵四边形ABCD是长方形,
∴AD=BC=10,CD=AB=8,∠B=∠C=90°.
根据折叠的性质,得 =8-DE, ,∠=∠B=90°.
在Rt△中,由勾股定理,得==6.
∴=10-6=4.
在Rt△中,由勾股定理,得.
∴(8-DE)2+42=DE2.
解得DE=5.
故答案是:5.
【点睛】
本题考查了折叠的性质,矩形的性质,勾股定理,熟练运用折叠的性质是本题的关键.
53.
【分析】
设CE=x,则BE=6﹣x由折叠性质可知,EF=CE=x,DF=CD=AB=10,所以AF=8,BF=AB﹣AF=10﹣8=2,在Rt△BEF中,BE2+BF2=EF2,即(6﹣x)2+22=x2,解得x=.
【详解】
解:设CE=x,则BE=6﹣x由折叠性质可知,EF=CE=x,DF=CD=AB=10,
在Rt△DAF中,AD=6,DF=10,
∴AF=8,
∴BF=AB﹣AF=10﹣8=2,
在Rt△BEF中,BE2+BF2=EF2,
即(6﹣x)2+22=x2,
解得x=,
故答案为.
【点睛】
本题考查了矩形,熟练掌握矩形的性质以及勾股定理是解题的关键.
54.5
【详解】
连接AC,FC,求出AC,利用三角形的中位线定理解决问题即可.
【解答】解:连接AC,FC.
由翻折的性质可知,BE垂直平分线段CF,
∴FM⊥BE,∴F.M,C共线,FM=MC,
∵AN=FN,∴MN=AC,
∵四边形ABCD是矩形,∴∠ABC=90°,
∴AC===10(cm),∴MN=AC=5(cm),
故答案为5.
【点评】本题考查翻折变换,矩形的性质,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题,属于中考常考题型.
55.115°
【分析】
先根据菱形性质求出∠BCD,∠ACE,再根据求出∠AEC,最后根据两直线平行,同旁内角互补解题即可.
【详解】
解:四边形ABCD是菱形,,
∴AB∥CD,
∴∠BCD=180°-∠B=130°,∠ACE=∠BCD=65°,
∵ ,
∴∠ACE=∠AEC=65°,
∴∠BAE=180°-∠AEC=115°.
【点睛】
本题考查了菱形性质,等腰三角形性质,解题方法较多,根据菱形性质求解∠ACE是解题关键.
56.
【分析】
根据菱形面积=对角线积的一半可求,再根据勾股定理求出,然后由菱形的面积即可得出结果.
【详解】
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴;
故答案为.
【点睛】
本题考查了菱形的性质、勾股定理以及菱形面积公式.熟练掌握菱形的性质,由勾股定理求出是解题的关键.
57.是
【分析】
如图(见解析),先根据“两张对边平行且相等的纸条”得出,再根据平行四边形的判定可得四边形ABCD是平行四边形,然后根据三角形全等的判定定理与性质可得,最后根据菱形的判定即可得.
【详解】
如图,过点B作,交DA延长线于点E,过点D作,交BA延长线于点F
由题意得:
四边形ABCD是平行四边形
在和中,
平行四边形ABCD是菱形
故答案为:是.
【点睛】
本题考查了平行四边形与菱形的判定、三角形全等的判定定理与性质等知识点,熟练掌握平行四边形与菱形的判定是解题关键.
58.
【分析】
设BE=x,根据菱形性质可得到AB= AD=CD=2x,进而得到,解得x值,根据勾股定理即可求得AE值.
【详解】
解:设BE=x,
∵菱形,
∴AB= AD=CD=2x,
∵,
∴,
∴BD=3x,
∴OB=OD=,
∴,
∴x=2,
∴AB=4,BE=2,
∴,
∴,
故答案为:.
【点睛】
本题考查菱形的性质结合勾股定理的应用,熟练掌握菱形性质是解题的关键.
59.
【详解】
试题分析:连接DB,BD与AC相交于点M,
∵四边形ABCD是菱形,∴AD=AB.AC⊥DB.
∵∠DAB=60°,∴△ADB是等边三角形.
∴DB=AD=1,∴BM=
∴AM=
∴AC=.
同理可得AE=AC=()2,AG=AE=()3,…
按此规律所作的第n个菱形的边长为()n-1
60.
【分析】
如图,连接AE、AF,先证明△GAE≌△HAF,由此可证得,进而同理可得,根据正方形ABCD的面积等于四个相同四边形的面积之和及小正方形的面积即可求得答案.
【详解】
解:如图,连接AE、AF,
∵点A为大正方形的中心,
∴AE=AF,∠EAF=90°,
∴∠AEF=∠AFE=45°,
∵∠GEF=90°,
∴∠AEG=∠GEF-∠AEF=45°,
∴∠AEG=∠AFE,
∵四边形ABCD为正方形,
∴∠DAB=∠EAF=90°,
∴∠GAE=∠HAF,
在△GAE与△HAF中,
∴△GAE≌△HAF(ASA),
∴,
∴,
即,
∵,
∴,
∴同理可得:,
即,
故答案为:.
【点睛】
本题考查了正方形的性质及全等三角形的判定及性质,熟练掌握正方形的性质并能作出正确的辅助线是解决本题的关键.
61.6
【分析】
连接ED交AC于一点F,连接BF,根据正方形的对称性得到此时△BFE的周长最小,利用勾股定理求出DE即可得到答案.
【详解】
解:连接ED交AC于一点F,连接BF,
∵四边形ABCD是正方形,
∴点B与点D关于AC对称,
∴BF=DF,
∴的周长=BF+EF+BE=DE+BE,此时周长最小,
∵正方形的边长为4,
∴AD=AB=4,∠DAB=90°,
∵点在上且,
∴AE=3,
∴DE=,
∴的周长=5+1=6,
故答案为:6.
【点睛】
此题主要考查了正方形的性质,依据正方形的对称性,连接DE交AC于点F时△BFE的周长有最小值是解题的关键.
62.①②④
【分析】
用正方形的性质和垂直的定义判断出四边形PECF是矩形,从而判定②正确;直接用正方形的性质和垂直得出①正确,利用全等三角形和矩形的性质得出④正确,由点P是正方形对角线上任意一点,说明AD和PD不一定相等,得出③错误.
【详解】
如图,
∵P为正方形ABCD的对角线BD上任一点,
∴PA=PC,∠C=90°,
∵过点P作PE⊥BC于点E,PF⊥CD,
∴∠PEC=∠DFP=∠PFC=∠C=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴PA=EF,故②正确,
∵BD是正方形ABCD的对角线,
∴∠ABD=∠BDC=∠DBC=45°,
∵∠PFC=∠C=90°,
∴PF∥BC,
∴∠DPF=45°,
∵∠DFP=90°,
∴△FPD是等腰直角三角形,故①正确,
在△PAB和△PCB中,
,
∴△PAB≌△PCB,
∴∠BAP=∠BCP,
在矩形PECF中,∠PFE=∠FPC=∠BCP,
∴∠PFE=∠BAP.故④正确,
∵点P是正方形对角线BD上任意一点,
∴AD不一定等于PD,
只有∠BAP=22.5°时,AD=PD,故③错误,
故答案为①②④.
【点睛】
考查了正方形的性质,矩形的判定和性质,全等三角形的判定和性质,垂直的定义,解本题的关键是判断出四边形PECF是矩形.
63.
【分析】
连接BD、DF,作于由B、D关于AC对称,推出,推出,根据垂线段最短可知,当D、F、E共线,且与DH重合时,的值最小,最小值为DH的长;
【详解】
解:连接BD、DF,作于H.
四边形ABCD是菱形,
,,
是等边三角形,
、D关于AC对称,
,
,
根据垂线段最短可知,当D、F、E共线,且与DH重合时,的值最小,最小值为DH的长,
在中,,
故答案为.
【点睛】
本题考查轴对称最短问题、菱形的性质、勾股定理、垂线段最短等知识,解题的关键是学会添加常用辅助线,学会利用垂线段最短解决最短问题.
64.2
【分析】
平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥AB时,OD最小,即DE最小,根据直角三角形勾股定理即可求解.
【详解】
解:如图
∵平行四边形ADCE的对角线的交点是AC的中点O,又AB=AC=4
∴OC=OA=AC=2
当OD⊥AB时,OD最小,即DE最小.
∵OD⊥BA,∠BAC=45°,
∴∠AOD=45°
∴△ADO为等腰直角三角形
在Rt△ADO由勾股定理可知
OD= AO=
∴DE=2OD=2
故答案为:2.
【点睛】
本题考查了勾股定理,平行四边形的性质,即平行四边形对角线互相平分,正确理解DE最小值的条件是关键.
65.证明见解析.
【分析】
利用平行四边形的性质得出 AO=CO,AD∥BC,进而得出∠EAC=∠FCO, 再利用 ASA 求出△AOE≌△COF,即可得出答案.
【详解】
∵ ABCD 的对角线 AC,BD 交于点 O,
∴AO=CO,AD∥BC,
∴∠EAC=∠FCO,
在△AOE 和△COF 中,
∴△AOE≌△COF(ASA),
∴AE=CF.
【点睛】
本题考查了全等三角形的判定与性质以及平行四边形的性质,熟练掌握全等三角形的判定方法是解题关键.
66.证明见解析.
【分析】
(1)一方面Rt△ABC中,由∠BAC=30°可以得到AB=2BC,另一方面△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,从而可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF.
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
【详解】
证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC.
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.
∵在Rt△AFE和Rt△BCA中,AF=BC,AE=BA,
∴△AFE≌△BCA(HL).∴AC=EF.
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD.
∴∠DAB=∠DAC+∠BAC=90°.∴EF∥AD.
∵AC=EF,AC=AD,∴EF=AD.
∴四边形ADFE是平行四边形.
考点:1.全等三角形的判定与性质;2.等边三角形的性质;3.平行四边形的判定.
67.(1)见解析;(2)OE=5,BG=2.
【分析】
(1)先证明EO是△DAB的中位线,再结合已知条件OG∥EF,得到四边形OEFG是平行四边形,再由条件EF⊥AB,得到四边形OEFG是矩形;
(2)先求出AE=5,由勾股定理进而得到AF=3,再由中位线定理得到OE=AB=AD=5,得到FG=5,最后BG=AB-AF-FG=2.
【详解】
解:(1)证明:∵四边形ABCD为菱形,
∴点O为BD的中点,
∵点E为AD中点,
∴OE为△ABD的中位线,
∴OE∥FG,
∵OG∥EF,∴四边形OEFG为平行四边形
∵EF⊥AB,∴平行四边形OEFG为矩形.
(2)∵点E为AD的中点,AD=10,
∴AE=
∵∠EFA=90°,EF=4,
∴在Rt△AEF中,.
∵四边形ABCD为菱形,
∴AB=AD=10,
∴OE=AB=5,
∵四边形OEFG为矩形,
∴FG=OE=5,
∴BG=AB-AF-FG=10-3-5=2.
故答案为:OE=5,BG=2.
【点睛】
本题考查了矩形的性质和判定,菱形的性质、勾股定理等知识点,特殊四边形的性质和判定属于中考常考题型,需要重点掌握.
68.(1)15°;(2)证明见解析.
【分析】
(1)如图1,利用旋转的性质得CA=DA,∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,再根据等腰三角形的性质求出∠ADC,从而计算出∠CDE的度数;
(2)如图2,利用直角三角形斜边上的中线性质得到BF=AC,利用含30度的直角三角形三边的关系得到BC=AC,则BF=BC,再根据旋转的性质得到∠BAE=∠CAD=60°,AB=AE,AC=AD ,DE=BC,从而得到DE=BF,△ACD和△BAE为等边三角形,接着由△AFD≌△CBA得到DF=BA,然后根据平行四边形的判定方法得到结论.
【详解】
解:(1)如图1,∵△ABC绕点A顺时针旋转α得到△AED,点E恰好在AC上,
∴∠CAD=∠BAC=30°,∠DEA=∠ABC=90°,
∵CA=DA,
∴∠ACD=∠ADC=(180° 30°)=75°,∠ADE=90°-30°=60°,
∴∠CDE=75° 60°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠BAC=30°,
∴BC=AC,
∴BF=BC,
∵△ABC绕点A顺时针旋转60°得到△AED,
∴∠BAE=∠CAD=60°,AB=AE,AC=AD,DE=BC,
∴DE=BF,△ACD和△BAE为等边三角形,
∴BE=AB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△AFD≌△CBA,
∴DF=BA,
∴DF=BE,
而BF=DE,
∴四边形BEDF是平行四边形.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.
69.见解析
【详解】
(1)由△ABC是等边三角形得到∠B=60°,而∠EFB=60°,由此可以证明EF∥DC,而DC=EF,然后即可证明四边形EFCD是平行四边形;
(2)如图,连接BE,由BF=EF,∠EFB=60°可以推出△EFB是等边三角形,然后得到EB=EF,∠EBF=60°,而DC=EF,由此得到EB=DC,又
△ABC是等边三角形,所以得到∠ACB=60°,AB=AC,然后即可证明△AEB≌△ADC,利用全等三角形的性质就证明AE=AD.
试题解析:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC(内错角相等,两直线平行),
∵DC=EF,
∴四边形EFCD是平行四边形;
(2)连接BE
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠EBF=60°
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠EBF=∠ACB,
∴△AEB≌△ADC,
∴AE=AD.
考点:1.平行四边形的判定;2.全等三角形的判定与性质;3.等边三角形的性质.
70.(1)见解析;(2)24
【分析】
(1)由四边形ABCD是平行四边形得出AB=CD,ABCD,进而得到∠BAC=∠DCA,再结合AO=CO,M,N分别是OA和OC中点即可求解;
(2)证明△ABO是等腰三角形,结合M是AO的中点,得到∠BMO=∠EMO=90°,同时△DOC也是等腰三角形,N是OC中点,得到∠DNO=90°,得到EMDN,再由(1)得到EM=DN,得出四边形EMND为矩形,进而求出面积.
【详解】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,ABCD,OA=OC,
∴∠BAC=∠DCA,
又点M,N分别为、的中点,
∴,
在和中,
,
∴.
(2)BD=2BO,又已知BD=2AB,
∴BO=AB,∴△ABO为等腰三角形;
又M为AO的中点,
∴由等腰三角形的“三线合一”性质可知:BM⊥AO,
∴∠BMO=∠EMO=90°,
同理可证△DOC也为等腰三角形,
又N是OC的中点,
∴由等腰三角形的“三线合一”性质可知:DN⊥CO,
∠DNO=90°,
∵∠EMO+∠DNO=90°+90°=180°,
∴EMDN,
又已知EM=BM,由(1)中知BM=DN,
∴EM=DN,
∴四边形EMND为平行四边形,
又∠EMO=90°,∴四边形EMND为矩形,
在Rt△ABM中,由勾股定理有:,
∴AM=CN=3,
∴MN=MO+ON=AM+CN=3+3=6,
∴.
故答案为:.
【点睛】
本题考查了平行四边形的性质、矩形的判定和性质、矩形的面积公式等,熟练掌握其性质和判定方法是解决此类题的关键.
71.(1)∠APB=90°; (2)△APB的周长是24cm.
【详解】
【分析】(1)根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB即可;
(2)求出AD=DP=5,BC=PC=5,求出DC=10=AB,即可求出答案.
【详解】(1)∵四边形是平行四边形,
∴∥ ,∥, ,
∴ ,
又∵和分别平分和,
∴ ,
∴ ;
(2) ∵平分,∥ ,
∴ ,
∴ ,同理: ,
∴ ,
在中, , ∴ ,
∴△的周长.
【点睛】本题考查了平行四边形的性质,等腰三角形的判定与性质等,熟练掌握平行四边形的性质是解题的关键.
72.(1)详见解析;(2)13.
【分析】
(1)只要证明DN∥BM,DM∥BN即可;
(2)只要证明△CEM≌△AFN,可得FN=EM=5,在Rt△AFN中,根据勾股定理AN=即可解决问题.
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,AN===13.
【点睛】
本题考查平行四边形的性质和判定、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
73.证明见解析.
【分析】
根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形式平行四边形,可得证明结论.
【详解】
如答图,连接BC,设对角线交于点O.
∵四边形ABCD是平行四边形,∴OA=OD,OB=OC.
∵AE=DF,OA﹣AE=OD﹣DF,∴OE=OF.
∴四边形BEDF是平行四边形.
74.(1)证明见解析;(2) ADEF的形状为菱形,理由见解析;(3)四边形AEGF是矩形,理由见解析.
【分析】
(1)根据平行线的性质得到∠BDE=∠A,根据题意得到∠DEF=∠BDE,根据平行线的判定定理得到AD∥EF,根据平行四边形的判定定理证明;
(2)根据三角形中位线定理得到DE=AC,得到AD=DE,根据菱形的判定定理证明;
(3)根据等腰三角形的性质得到AE⊥EG,根据有一个角是直角的平行四边形是矩形证明.
【详解】
(1)证明:∵DE∥AC,
∴∠BDE=∠A,
∵∠DEF=∠A,
∴∠DEF=∠BDE,
∴AD∥EF,又∵DE∥AC,
∴四边形ADEF为平行四边形;
(2)解:□ADEF的形状为菱形,
理由如下:∵点D为AB中点,
∴AD=AB,
∵DE∥AC,点D为AB中点,
∴DE=AC,
∵AB=AC,
∴AD=DE,
∴平行四边形ADEF为菱形,
(3)四边形AEGF是矩形,
理由如下:由(1)得,四边形ADEF为平行四边形,
∴AF∥DE,AF=DE,
∵EG=DE,
∴AF∥DE,AF=GE,
∴四边形AEGF是平行四边形,
∵AD=AG,EG=DE,
∴AE⊥EG,
∴四边形AEGF是矩形.
故答案为(1)证明见解析;(2)菱形;(3)矩形.
【点睛】
本题考查的是平行四边形、矩形、菱形的判定,掌握它们的判定定理是解题的关键.
75.证明见解析
【分析】
(1)利用平行四边形的性质得出∠5=∠3,∠AEB=∠4,进而利用全等三角形的判定得出即可;
(2)利用全等三角形的性质得出AE=CF,进而得出四边形AECF是平行四边形,即可得出答案.
【详解】
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠5=∠3,
∵∠1=∠2,
∴∠AEB=∠4,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)由(1)得△ABE≌△CDF,
∴AE=CF,
∵∠1=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF∥CE.
76.(1)见解析;(2)见解析.
【分析】
(1)先证明,再利用SSS证明;
(2)根据“一组对边平行且相等的四边形是平行四边形”证明四边形是平行四边形即可.
【详解】
证明:
即
证明:
四边形是平行四边形.
【点睛】
本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形的判定方法,证明三角形全等是解决问题的关键.
77.(1)证明见解析;(2).
【分析】
(1)由平行四边形的判定得出四边形OCED是平行四边形,根据矩形的性质求出OC=OD,根据菱形的判定得出即可.(2)解直角三角形求出BC=2.AB=DC=2,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=BC=1,求出OE=2OF=2,求出菱形的面积即可.
【详解】
证明:,,
四边形OCED是平行四边形,
矩形ABCD,,,,
,
四边形OCED是菱形;
在矩形ABCD中,,,,
,
,
连接OE,交CD于点F,
四边形OCED为菱形,
为CD中点,
为BD中点,
,
,
.
【点睛】
本题主要考查了矩形的性质和菱形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:菱形的面积等于对角线积的一半.
78.(1);(2)见解析
【分析】
(1)利用三角形内角和定理求出,利用角平分线的定义求出,再利用平行线的性质解决问题即可.
(2)证明可得结论.
【详解】
(1)解:,
,
,
,
平分,
,
四边形是平行四边形,
,
,
(2)证明:四边形是平行四边形,
,
,,
,
,
,
.
【点睛】
本题考查平行四边形的性质,全等三角形的判定和性质等知识,解题的关键是熟练掌握相关的知识点.
79.(1)见解析 (2)9
【分析】
(1)先证明Rt△ABE≌Rt△CDF,得到AB∥CD,即可判定平行四边形;
(2)证明AB=GB,根据勾股定理构造方程,解方程即可求解.
【详解】
解:(1)∵AF=CE,
∴AF-EF=CE-EF,
∴AE=CF,
∵BE⊥AC,DF⊥AC,,
∴∠AEB=∠CFD=90°,
∵AB=CD,
∴Rt△ABE≌Rt△CDF,
∴∠BAE=∠DCF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,∠DAB=∠BCD,
∴∠AGB=∠GBC,
∵∠GBC=∠BCD,
∴∠AGB=∠BAG,
∴AB=GB,
设AB=GB=x,则BE=x-2,
∵BG⊥AC,
∴,
∴ ,
解得x=9,
∴AB=9.
【点睛】
本题考查了平行四边的判定与性质,勾股定理,等腰三角形判定等知识,综合性较强,熟知相关定理并根据已知条件合理选择定理是解题关键.
80.(1)见解析;(2)四边形 是菱形,理由见解析;(3)当 时,四边形 是正方形.理由见解析.
【分析】
(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)当=45°,由()可知,四边形 是菱形,可得,则四边形BECD是正方形.
【详解】
(1) ,
,
,
,
,
,即 ,
四边形 是平行四边形,
.
(2) 四边形 是菱形,
理由是: 点 为 中点,
,
,
,
,
四边形 是平行四边形,
,点 为 中点,
,
四边形 是菱形.
(3) 当 时,
,
,
由()可知,四边形 是菱形,
,
,
四边形 是正方形.
【点睛】
本题考查了平行四边形的性质和判定,菱形的判定,正方形的判定、直角三角形的性质的应用,灵活运用所学知识解决问题是解题的关键.
81.(1)见解析(2)菱形,见解析
【分析】
(1)利用SAS证明≌即可求解;
(2)先证明四边形是平行四边形,再证明对角线互相垂直即可得到为菱形.
【详解】
(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠ADB=∠CBD,
又∵∠ADB+∠ADE=180°,∠CBF+∠CBD=180°,
∴∠ADE=∠CBF
在△ADE和△CBF中
∴△ADE≌△CBF;
(2)四边形是菱形
理由如下:
如图,连接,,
由(1)得△ADE≌△CBF
∴CF=AE, ∠E=∠F
∴AE∥CF
∴AECF
∴四边形AFCE是平行四边形
当BD平分∠ABC时,∠ABD=∠CBD
又∵AD∥CB,
∴∠ADB=∠DBC
∴∠ABD=∠ABD
∴AD=AB=BC
∴△ABC为等腰三角形
由等腰三角形性质三线合一可得AC⊥EF
∴平行四边形AFCE是菱形
【点睛】
此题主要考查特殊平行四边形的性质与判定,解题的关键是熟知菱形的判定定理.
82.(1)见解析;(2)见解析
【分析】
(1)根据平行四边形的性质得到AB=CD,∠DAE=∠AEB,利用AE平分∠BAD,推出∠BAE=∠AEB,得到BE=AB,即可得到结论;
(2)根据BE=AB,BF平分∠ABE,得到AF=EF,证明△ADF≌△ECF,推出DF=CF,即可得到结论.
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF,
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
【点睛】
此题考查平行四边形的判定及性质,全等三角形的判定及性质,等腰三角形三线合一的性质,熟记各知识点并应用解决问题是解题的关键.
83.(1)证明见解析;(2)四边形ABDE是平行四边形;(3)当∠BAC=90°时,四边形ADCE是正方形,证明见解析
【分析】
(1)由等腰三角形的性质可得AD⊥BC,∠BAD=∠CAD,又由AN为△ABC的外角∠CAM的平分线,可得∠DAE=90°,又由CE⊥AN,由矩形的判定可证四边形ADCE为矩形;
(2)利用(1)中矩形的对角线相等推知:AC=DE;结合已知条件可以推知AB∥DE,又AE=BD,则易判定四边形ABDE是平行四边形;
(3)由等腰直角三角形的性质可得AD=CD=BD,即可证四边形ADCE是正方形.
【详解】
证明:(1)∵在△ABC中,AB=AC,AD为∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)四边形ABDE是平行四边形,
理由如下:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形;
(3)当∠BAC=90°时,四边形ADCE是正方形,
理由:∵∠BAC=90°,AB=AC,AD为∠BAC的平分线,
∴AD=CD=BD,
又∵四边形ADCE是矩形,
∴四边形ADCE是正方形.
【点睛】
本题考查平行四边形、矩形和正方形的判定方法,掌握特殊四边形的判定定理是解题的关键.
84.(1)证明见解析;(2)证明见解析;(3)等腰直角三角形,证明见解析;(4)12.5.
【分析】
【详解】
(1)由平行四边形的性质得出,∠BAD=∠BCD,BC∥AD,证出∠1=∠2,再证出∠2=∠3,得出AE∥CF,即可得出结论;
(2)由四边形AHCF是平行四边形,得出AF=CH,再证出CH=EC,即可得出AF=EC;
(3)连接AG,过G作GN∥BC交AB于N,先证四边形ABCD是矩形,得出∠GNB=90°,BC∥GN∥AD,再证出NG是AB的垂直平分线,得出BG=AG,得出∠BGN=∠AGN,然后证明△AFG≌△ECG,得出AG=EG=BG,∠EGC=∠AGF,∠GAF=∠GEC,再证出∠BGE=90°,即可得出结论;
(4)作GM⊥AD于M,则GM∥CD,由矩形的性质得出∠D=∠BCD=90°,CD=AB,AD=BC,再证出△DCF、△MGF是等腰直角三角形,得出FD=CD=6,GM=FM,证明GM为△DCF的中位线,得出FM=GM═DM=CD=3,求出AM,由勾股定理求出AG,得出BG、EG,即可求出△BEG的面积.
(1)证明:如图1所示:
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,BC∥AD,
∴∠1=∠2,
∵CF平分∠BCD,AE平分∠BAD,
∴∠1=∠4=∠BCD,∠3=∠BAD,
∴∠1=∠3,
∴∠2=∠3,
∴AE∥CF,
∴四边形AHCF是平行四边形;
(2)证明:∵四边形AHCF是平行四边形,
∴AF=CH,
∵AE∥CF,
∴∠E=∠4,∠5=∠1,
∴∠E=∠5,
∴CH=EC,
∴AF=EC;
(3)解:△BEG是等腰直角三角形;理由如下:
连接AG,过G作GN∥BC交AB于N,如图2所示:
∵四边形ABCD是平行四边形,∠BAD=90°,
∴四边形ABCD是矩形,
∴BC∥AD,∠CBN=90°,
∴∠GNB=90°,BC∥GN∥AD,
∵G为CF的中点,
∴N为AB中点,
即NG是AB的垂直平分线,
∴BG=AG,
∴∠BGN=∠AGN,
∵NG∥AD,
∴∠AGN=∠GAF=∠BGN,
∵CF平分∠BCD,∠BCD=90°,
∴∠DCF=90°,∠DCF=45°,
∴∠DFC=45°,
∴∠ECG=∠AFC=90°+45°=135°,
在△AFG和△ECG中,
,
∴△AFG≌△ECG(SAS),
∴AG=EG=BG,∠EGC=∠AGF,∠GAF=∠GEC,
∵∠AGN=∠GAF=∠BGN,
∴∠AGN=∠GAF=∠BGN=∠GEC,
∵∠GAF+∠AGF=180°-135°=45°,
∴∠EGC+∠BGF=2(∠GAF+∠AGF)=90°,
即∠BGE=90°,
∴△BEG是等腰直角三角形;
(4)作GM⊥AD于M,如图2所示:
则GM∥CD,
∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,CD=AB=6,AD=BC=7,
∴∠DCF=45°,
∴∠DFC=45°,
∴△DCF、△MGF是等腰直角三角形,
∴FD=CD=6,GM=FM,
∵G为CF的中点,
∴GM为△DCF的中位线,
∴FM=GM═DM=CD=3,
∴AM=7-3=4,
∴AG=,
∴BG=EG=5,
∴△BEG的面积=BG EG=.
85.(1)见解析;(2)
【分析】
(1)连接交于点,根据平行四边形的性质可以判定OF为△DBE的中位线,即可证明;
(2)根据AD=2,∠ACD=90°,∠ADC=60°,可求出AC的长,再根据中位线的性质即可求解;
【详解】
解:(1)连接交于点,
∵四边形是平行四边形,
∴,
∵,
∴OF为△DBE的中位线
∴.
(2)∵AD=2,∠ACD=90°,∠ADC=60°,
∴.
∵是的中位线,
∴.
∴.
∵,
∴.
【点睛】
本题考查了三角形中位线的性质以及平行四边形的性质,正确掌握知识点是解题的关键;
86.(1)见解析;(2)2
【分析】
(1)利用中位线性质可得,.,.可证四边形是平行四边形.由平行四边形性质可得,.
(2)由和,可推得.求由点是中点,.由三等分可求.根据平行四边形性质可得四边形的面积.
【详解】
(1)证明:∵点,分别是,的中点,
∴,.
∵点,分别是,的中点,
∴,.
∴,.
∴四边形是平行四边形.
∴,;
(2)解:∵,
∴.
又∵,
∴.
∵,,
∵,
∵点是中点,
∴.
∴.
∴四边形的面积.
【点睛】
本题考查中位线性质,平行四边形的判定与性质,中线的性质,掌握中位线性质,平行四边形的判定与性质,中线的性质,注意中线与中位线的区别以及它们性质是解题关键.
87.证明:在ABCD中,AD=BC且AD∥BC,
∵BE=FD,∴AF=CE.
∴四边形AECF是平行四边形
【详解】
试题分析:根据平行四边形的性质可得AF∥EC.AF=EC,然后根据平行四边形的定义即可证得.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E,F分别是BC,AD的中点,
∴,,
∴AF∥EC,AF=EC,
∴四边形AECF是平行四边形.
【点评】本题考查了平行四边形的性质与判定;熟练掌握平行四边形的性质,证出AF=EC是解决问题的关键.
88.(1)证明见解析;(2),证明见解析;(3)=3.
【分析】
(1)证明△AGE≌△ACE,根据全等三角形的性质可得到GE=EC,再利用三角形的中位线定理证明DE∥AB,再加上条件EF∥BC可证出结论;
(2)先证明BF=DE=BG,再证明AG=AC,可得到BF=(AB AG)=(AB AC);
(3) 根据△DCE中DC边上的高与BDEF中BD边上的高相等,得出BDEF的面积为6,设BDEF中BF边上的高为h,由即可求解.
【详解】
(1)延长交于点,
,,
又∵平分,
∴∠GAE=∠CAE
在和中,,
,
,
∵点是边的中点,
∴
为的中位线,
,
,
四边形是平行四边形.
(2)四边形是平行四边形,
,
,分别是,的中点,
,
,
,
.
(3)如图:
∵BD=DC,EF∥BC
∴△DCE中DC边上的高与BDEF中BD边上的高相等,
∴
∵BF∥DE
设BDEF中BF边上的高为h,
则
=(DE+BP)×h÷2-BP×h÷2
=DE×h÷2
=6÷2
=3.
【点睛】
此题主要考查了平行四边形的判定与性质,全等三角形的判定与性质,三角形中位线定理,以及等底同高的平行四边形和三角形的面积之间的关系,证明GE=EC,再利用三角形中位线定理证明DE∥AB是解决问题的关键.
答案第1页,共2页
