浙江省义乌市稠州中学教育集团2021-2022学年九年级下学期寒假检测数学试题(word版 含答案)
文档属性
| 名称 | 浙江省义乌市稠州中学教育集团2021-2022学年九年级下学期寒假检测数学试题(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 549.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 14:40:49 | ||
图片预览




文档简介
2022年稠州中学教育集团九年级寒假作业检查数学试题(2022.2.16)
一、选择题(本题有10小题,每小题3分,共30分)
1.实数,,2,-3中,为负整数的是( )
A. B. C.2 D.-3
2.下列运算正确的是( )
A.2x+3x=5x2 B.(﹣2x)3=﹣6x3 C.2x3 3x2=6x5 D.(3x+2)(2﹣3x)=9x2﹣4
3.如图是由5个小正方体组合成的几何体,则其俯视图为( )
A. B. C. D.
4.在一次数学测试中,小明成绩72分,超过班级半数同学的成绩,分折得出这个结论所用的统计量是( ) A.中位数 B.众数 C.平均数 D.方差
5.关于x的方程(x﹣1)(x+2)=p2(p为常数)的根的情况,下列结论中正确的是( )
A.两个正根 B.两个负根 C.一个正根,一个负根 D.无实数根
6.图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A. B. C. D.
7.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( ) A.60° B.65° C.68° D.70°
如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.
若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A. cm2 B.(36)cm2 C. cm2 D. cm2
9.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:
①abc<0,②2a+b>0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
如图,正方形的边长为a,点E在边上运动(不与点A,B重合),,点F在射线上,且与相交于点G,连接.则下列结论:①,②的周长为,③;④当时,G是线段的中点,其中正确的结论是( )
A.①②③ B.①④ C.①③④ D.①②③④
二、填空题 (本题有6小题,每小题4分,共24分)
11. 第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为 .
12.已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是 .
13.将二次函数y=x2+2x-3的图象绕原点旋转180°,若得到的新的函数图象上总有两个点在直线y=x-m上,则m的取值范围是 .
14.如图,点A是双曲线y(x<0)上一动点,连接OA,作OB⊥OA,且使OB=2OA,当点A在双曲线y上运动时,点B在双曲线y上移动,则k的值为 .
15..如图,在△ABC中,∠B=45°,AB=6,D、E分别是AB、AC的中点,连接DE,在直线DE和直线BC上分别取点F、G,连接BF、DG.若BF=2DG,且直线BF与直线DG互相垂直,则BG的长为 .
16.图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=14,AB=BC=CQ=QA=6,OQ=5,O,P两点间距离与OQ长度相等.当OQ绕点O转动时,点A,B,C的位置随之改变.
(1)点P、Q之间距离的最大值为 ;
(2)在转动过程中,则PQ PB= .
三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)
17.(本题6分)
(1)计算:
(2)已知,求的值.
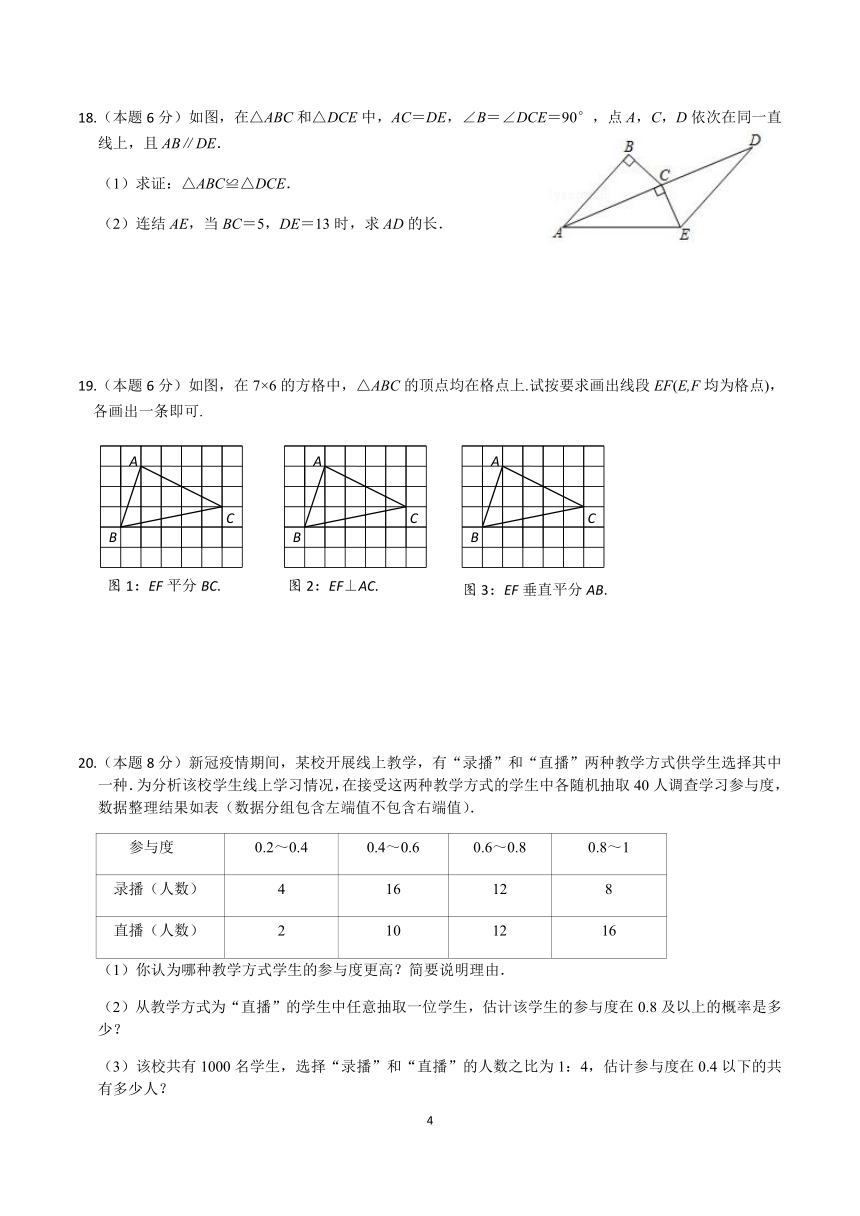
18.(本题6分)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE.
(2)连结AE,当BC=5,DE=13时,求AD的长.
19.(本题6分)如图,在7×6的方格中,△ABC的顶点均在格点上.试按要求画出线段EF(E,F均为格点),各画出一条即可.
20.(本题8分)新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 0.2~0.4 0.4~0.6 0.6~0.8 0.8~1
录播(人数) 4 16 12 8
直播(人数) 2 10 12 16
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有1000名学生,选择“录播”和“直播”的人数之比为1:4,估计参与度在0.4以下的共有多少人?
21.(本题8分) 如图,在平行四边形ABCD中,AC是对角线,∠CAB=90°,以点A为圆心,以AB的长为半径作⊙A,交BC边于点E,交AC于点F,连接DE.(1)求证:DE与⊙A相切;
(2)若∠ABC=60°,AB=6,求阴影部分的面积.
22.(本题10分)某经销商3月份用11000元购进一批T恤衫售完后,4月份用24 000元购进一批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.
(1)4月份进了这批T恤衫多少件?
(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.
①用含a的代数式表示b.
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
23.(本题10分)在平面直角坐标系xOy中,抛物线y=ax2-4ax-5a(a 0).
(1)抛物线与x轴交于A、B两点(点A在点B的左侧),求点A 和点B 的坐标;
(2)若点P(m,n)是抛物线上的一点,在a>0的条件下,当 m≥0时,n 的取值范围是n≥-9,求抛物线的解析式;
(3)当a=1时,把抛物线y=ax2-4ax-5a向上平移m(m>0)个单位长度得到新抛物线G,设新抛物线G与x 轴的一个交点的横坐标为t,且t满足24.(本题12分)在平面直角坐标系中,点A的坐标为,点B在直线l:上,过点B作AB的垂线,过原点O作直线l的垂线,两垂线相交于点C.
(1)如图,点B,C分别在第三、二象限内,BC与AO相交于点D,若BA=BO.
①求证:CD=CO.
②求四边形ABOC的面积.
(2)是否存在点B,使得以A,B,C为顶点的三角形与△BCO相似?若存在,求OB的长;若
不存在,请说明理由.
2022年稠州中学九年级寒假作业检查数学参考答案
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A A C B A D C B
10.解:如图1中,在BC上截取BH=BE,连接EH.
∵BE=BH,∠EBH=90°,∴EH=BE,
∵AF=BE,∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,∴AE=HC,∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECB,
∵∠ECH+∠CEB=90°,∴∠AEF+∠CEB=90°,∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确,
如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,∴∠ECH=∠BCD=90°,∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,∴△GCE≌△GCH(SAS),∴EG=GH,
∵GH=DG+DH,DH=BE,∴EG=BE+DG,故③错误,
∴△AEG的周长=AE+EG+AG=AE+AH=AD+DH+AE=AE+EB+AD=AB+AD=2a,故②错误,
当BE=a时,设DG=x,则EG=x+a,
在Rt△AEG中,则有(x+a)2=(a-x)2+(a)2,解得x=,∴AG=GD,故④正确,
故答案为:①④正确.选B
二、填空题 (本题有6小题,每小题4分,共24分)
11.; 12.; 13. ; 14. -4 ;;16.(1)10;(2)160.
16. 解:(1)由题意可得,点Q在点O为圆心,半径长为5的圆上,
∴当点Q为PO的延长线于圆O的交点时,P、Q两点间的距离最大,为10.故答案为:10.
(2)以特殊位置法求PQ PB的值,
如图,点P、O、Q在同一条直线上时,PQ=10,连接BQ、AC交于点H,
∵AB=BC=CQ=QA,∴四边形ABCQ为菱形,∴BQ⊥AC,QH=BH,
设QH=BH=x,则PH=PQ+QH=10+x,
在Rt△PCH中,CH2=PC2﹣PH2,
在Rt△QCH中,CH2=QC2﹣QH2,∴PC2﹣PH2=QC2﹣QH2,
∵PC=14,CQ=6,∴142﹣(10+x)2=62﹣x2,解得:x=3,
∴PB=PQ+QH+BH=10+x+x=10+3+3=16,
∴PQ PB=10×16=160. 故答案为:160.
三、解答题:
17. (1)解:原式 = ----3分
(2)解:原式 ----2分
当 时,原式 ----1分
18. (1)∵AB∥DE,∴∠BAC=∠D,
又∵∠B=∠DCE=90°,AC=DE,
∴△ABC≌△DCE(AAS); ----3分
(2)AD=25. ----3分
解:
每小题2分
20. 解:(1)“直播”教学方式学生的参与度更高:
理由:“直播”参与度在0.6以上的人数为28人,“录播”参与度在0.6以上的人数为20人,参与度在0.6以上的“直播”人数远多于“录播”人数,
所以“直播”教学方式学生的参与度更高; ----2分
(2)16÷40=0.4=40%,
答:估计该学生的参与度在0.8及以上的概率是40%; ----3分
(3)“录播”总学生数为1000200(人),“直播”总学生数为1000800(人),
所以“录播”参与度在0.4以下的学生数为20020(人),
“直播”参与度在0.4以下的学生数为80040(人),
所以参与度在0.4以下的学生共有20+40=60(人). ----3分
解:(1)证明:连接AE,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠AEB,
∵AE=AB,∴∠AEB=∠ABC,∴∠DAE=∠ABC,
∴△AED≌△BAC(AAS), ----2分
∴∠DEA=∠CAB,
∵∠CAB=90°,∴∠DEA=90°,∴DE⊥AE,
∵AE是⊙A的半径,∴DE与⊙A相切; ----2分
(2)解:∵∠ABC=60°,AB=AE=6,
∴△ABE是等边三角形,∴AE=BE,∠EAB=60°,
∵∠CAB=90°,
∴∠CAE=90°﹣∠EAB=90°﹣60°=30°,
∠ACB=90°﹣∠B=90°﹣60°=30°,
∴∠CAE=∠ACB,
∴AE=CE,∴CE=BE,∴S△ABCAB AC,
∴S△ACES△ABC, ----2分
∵∠CAE=30°,AE=6,
∴S扇形AEF,
∴S阴影=S△ACE﹣S扇形AEF=9. ----2分
22. 解:(1)设3月份购进x件T恤衫,
,解得,x=100,经检验,x=100是原分式方程的解,则2x=200,
答:4月份进了这批T恤衫200件; ----3分
(2)①每件T恤衫的进价为:24000÷200=120(元),
(180﹣120)a+(180×0.8﹣120)(100﹣a)=(180﹣120)a+(180×0.9﹣120)b+(180×0.7﹣120)(100﹣a﹣b)化简,得b; ----3分
②设乙店的利润为w元,
w=(180﹣120)a+(180×0.9﹣120)b+(180×0.7﹣120)(100﹣a﹣b)
=54a+36b+600=54a+36600=36a+2400, ----2分
∵乙店按标价售出的数量不超过九折售出的数量,∴a≤b,即a,解得,a≤,
∵a为正整数 ∴当a=33时,w取得最大值,此时w=3588,
答:乙店利润的最大值是3588元. ----2分
23. (1)解:由题意可令y=0时,则有:
,解得: ,
∴点A、B的坐标分别为 、 ----3分
(2)解:由题意得: ,
∵当m≥0时,n 的取值范围是n≥-9,
∴顶点的纵坐标为-9,即 ,
∴ ,
∴抛物线的解析式为 ----3分
(3)解:当a=1时,则有: ,
设抛物线向上平移m(m>0)个单位长度得到新抛物线G的解析式为 ,
由(2)可知抛物线 的顶点坐标为 ,
∴当抛物线 向上平移9个单位长度时,此时抛物线G与x轴只有一个交点为 ,
∴m=9 ----2分
当抛物线G上的一个点为 时,即 ,
解得: ,
∴m 的取值范围为 ----2分
24.(本题12分)
解:(1)①证明:如图1,
∵BA=BO, ∴
∵BA⊥BC, ∴
而
∴
∵OB⊥OC,∴
∴
∴ ----3分
②如图2,分别过点A、B、C作AH⊥OB于点H,BM⊥OA于点M,CN⊥OA于点N,
由题意可知,
在Rt△AHO中,设AH=m,OH=3m.
∵,∴,解得m=4.
∴
∵∴,
∴,
∵ ∴
∴
∴
∴ ∴
∴. ----4分
(2)过点A作AH⊥OB于点H,则有AH=4,OH=12.
①如图3,当点C在第二象限内,时,设
又
,
,
∴整理得解得
②如图4,当点C在第二象限内, 时,
延长AB,CO交于点G,则,
又
而∠ABH=∠GBO,
③当点C在第四象限内,时,AC与OB相交于点E,则有
(a)如图5,点B在第三象限内.
在中,
又
而∠AEH=∠CEO,
(b)如图6,点B在第一象限内.
在中,
又
而∠AEH=∠CEO,
综上所述,OB的长为 ---- 每答对1个解给1分
一、选择题(本题有10小题,每小题3分,共30分)
1.实数,,2,-3中,为负整数的是( )
A. B. C.2 D.-3
2.下列运算正确的是( )
A.2x+3x=5x2 B.(﹣2x)3=﹣6x3 C.2x3 3x2=6x5 D.(3x+2)(2﹣3x)=9x2﹣4
3.如图是由5个小正方体组合成的几何体,则其俯视图为( )
A. B. C. D.
4.在一次数学测试中,小明成绩72分,超过班级半数同学的成绩,分折得出这个结论所用的统计量是( ) A.中位数 B.众数 C.平均数 D.方差
5.关于x的方程(x﹣1)(x+2)=p2(p为常数)的根的情况,下列结论中正确的是( )
A.两个正根 B.两个负根 C.一个正根,一个负根 D.无实数根
6.图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A. B. C. D.
7.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( ) A.60° B.65° C.68° D.70°
如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.
若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A. cm2 B.(36)cm2 C. cm2 D. cm2
9.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:
①abc<0,②2a+b>0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
如图,正方形的边长为a,点E在边上运动(不与点A,B重合),,点F在射线上,且与相交于点G,连接.则下列结论:①,②的周长为,③;④当时,G是线段的中点,其中正确的结论是( )
A.①②③ B.①④ C.①③④ D.①②③④
二、填空题 (本题有6小题,每小题4分,共24分)
11. 第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为 .
12.已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是 .
13.将二次函数y=x2+2x-3的图象绕原点旋转180°,若得到的新的函数图象上总有两个点在直线y=x-m上,则m的取值范围是 .
14.如图,点A是双曲线y(x<0)上一动点,连接OA,作OB⊥OA,且使OB=2OA,当点A在双曲线y上运动时,点B在双曲线y上移动,则k的值为 .
15..如图,在△ABC中,∠B=45°,AB=6,D、E分别是AB、AC的中点,连接DE,在直线DE和直线BC上分别取点F、G,连接BF、DG.若BF=2DG,且直线BF与直线DG互相垂直,则BG的长为 .
16.图1是由七根连杆链接而成的机械装置,图2是其示意图.已知O,P两点固定,连杆PA=PC=14,AB=BC=CQ=QA=6,OQ=5,O,P两点间距离与OQ长度相等.当OQ绕点O转动时,点A,B,C的位置随之改变.
(1)点P、Q之间距离的最大值为 ;
(2)在转动过程中,则PQ PB= .
三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)
17.(本题6分)
(1)计算:
(2)已知,求的值.
18.(本题6分)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE.
(2)连结AE,当BC=5,DE=13时,求AD的长.
19.(本题6分)如图,在7×6的方格中,△ABC的顶点均在格点上.试按要求画出线段EF(E,F均为格点),各画出一条即可.
20.(本题8分)新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 0.2~0.4 0.4~0.6 0.6~0.8 0.8~1
录播(人数) 4 16 12 8
直播(人数) 2 10 12 16
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有1000名学生,选择“录播”和“直播”的人数之比为1:4,估计参与度在0.4以下的共有多少人?
21.(本题8分) 如图,在平行四边形ABCD中,AC是对角线,∠CAB=90°,以点A为圆心,以AB的长为半径作⊙A,交BC边于点E,交AC于点F,连接DE.(1)求证:DE与⊙A相切;
(2)若∠ABC=60°,AB=6,求阴影部分的面积.
22.(本题10分)某经销商3月份用11000元购进一批T恤衫售完后,4月份用24 000元购进一批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.
(1)4月份进了这批T恤衫多少件?
(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.
①用含a的代数式表示b.
②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.
23.(本题10分)在平面直角坐标系xOy中,抛物线y=ax2-4ax-5a(a 0).
(1)抛物线与x轴交于A、B两点(点A在点B的左侧),求点A 和点B 的坐标;
(2)若点P(m,n)是抛物线上的一点,在a>0的条件下,当 m≥0时,n 的取值范围是n≥-9,求抛物线的解析式;
(3)当a=1时,把抛物线y=ax2-4ax-5a向上平移m(m>0)个单位长度得到新抛物线G,设新抛物线G与x 轴的一个交点的横坐标为t,且t满足
(1)如图,点B,C分别在第三、二象限内,BC与AO相交于点D,若BA=BO.
①求证:CD=CO.
②求四边形ABOC的面积.
(2)是否存在点B,使得以A,B,C为顶点的三角形与△BCO相似?若存在,求OB的长;若
不存在,请说明理由.
2022年稠州中学九年级寒假作业检查数学参考答案
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A A C B A D C B
10.解:如图1中,在BC上截取BH=BE,连接EH.
∵BE=BH,∠EBH=90°,∴EH=BE,
∵AF=BE,∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,∴AE=HC,∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECB,
∵∠ECH+∠CEB=90°,∴∠AEF+∠CEB=90°,∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确,
如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,∴∠ECH=∠BCD=90°,∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,∴△GCE≌△GCH(SAS),∴EG=GH,
∵GH=DG+DH,DH=BE,∴EG=BE+DG,故③错误,
∴△AEG的周长=AE+EG+AG=AE+AH=AD+DH+AE=AE+EB+AD=AB+AD=2a,故②错误,
当BE=a时,设DG=x,则EG=x+a,
在Rt△AEG中,则有(x+a)2=(a-x)2+(a)2,解得x=,∴AG=GD,故④正确,
故答案为:①④正确.选B
二、填空题 (本题有6小题,每小题4分,共24分)
11.; 12.; 13. ; 14. -4 ;;16.(1)10;(2)160.
16. 解:(1)由题意可得,点Q在点O为圆心,半径长为5的圆上,
∴当点Q为PO的延长线于圆O的交点时,P、Q两点间的距离最大,为10.故答案为:10.
(2)以特殊位置法求PQ PB的值,
如图,点P、O、Q在同一条直线上时,PQ=10,连接BQ、AC交于点H,
∵AB=BC=CQ=QA,∴四边形ABCQ为菱形,∴BQ⊥AC,QH=BH,
设QH=BH=x,则PH=PQ+QH=10+x,
在Rt△PCH中,CH2=PC2﹣PH2,
在Rt△QCH中,CH2=QC2﹣QH2,∴PC2﹣PH2=QC2﹣QH2,
∵PC=14,CQ=6,∴142﹣(10+x)2=62﹣x2,解得:x=3,
∴PB=PQ+QH+BH=10+x+x=10+3+3=16,
∴PQ PB=10×16=160. 故答案为:160.
三、解答题:
17. (1)解:原式 = ----3分
(2)解:原式 ----2分
当 时,原式 ----1分
18. (1)∵AB∥DE,∴∠BAC=∠D,
又∵∠B=∠DCE=90°,AC=DE,
∴△ABC≌△DCE(AAS); ----3分
(2)AD=25. ----3分
解:
每小题2分
20. 解:(1)“直播”教学方式学生的参与度更高:
理由:“直播”参与度在0.6以上的人数为28人,“录播”参与度在0.6以上的人数为20人,参与度在0.6以上的“直播”人数远多于“录播”人数,
所以“直播”教学方式学生的参与度更高; ----2分
(2)16÷40=0.4=40%,
答:估计该学生的参与度在0.8及以上的概率是40%; ----3分
(3)“录播”总学生数为1000200(人),“直播”总学生数为1000800(人),
所以“录播”参与度在0.4以下的学生数为20020(人),
“直播”参与度在0.4以下的学生数为80040(人),
所以参与度在0.4以下的学生共有20+40=60(人). ----3分
解:(1)证明:连接AE,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAE=∠AEB,
∵AE=AB,∴∠AEB=∠ABC,∴∠DAE=∠ABC,
∴△AED≌△BAC(AAS), ----2分
∴∠DEA=∠CAB,
∵∠CAB=90°,∴∠DEA=90°,∴DE⊥AE,
∵AE是⊙A的半径,∴DE与⊙A相切; ----2分
(2)解:∵∠ABC=60°,AB=AE=6,
∴△ABE是等边三角形,∴AE=BE,∠EAB=60°,
∵∠CAB=90°,
∴∠CAE=90°﹣∠EAB=90°﹣60°=30°,
∠ACB=90°﹣∠B=90°﹣60°=30°,
∴∠CAE=∠ACB,
∴AE=CE,∴CE=BE,∴S△ABCAB AC,
∴S△ACES△ABC, ----2分
∵∠CAE=30°,AE=6,
∴S扇形AEF,
∴S阴影=S△ACE﹣S扇形AEF=9. ----2分
22. 解:(1)设3月份购进x件T恤衫,
,解得,x=100,经检验,x=100是原分式方程的解,则2x=200,
答:4月份进了这批T恤衫200件; ----3分
(2)①每件T恤衫的进价为:24000÷200=120(元),
(180﹣120)a+(180×0.8﹣120)(100﹣a)=(180﹣120)a+(180×0.9﹣120)b+(180×0.7﹣120)(100﹣a﹣b)化简,得b; ----3分
②设乙店的利润为w元,
w=(180﹣120)a+(180×0.9﹣120)b+(180×0.7﹣120)(100﹣a﹣b)
=54a+36b+600=54a+36600=36a+2400, ----2分
∵乙店按标价售出的数量不超过九折售出的数量,∴a≤b,即a,解得,a≤,
∵a为正整数 ∴当a=33时,w取得最大值,此时w=3588,
答:乙店利润的最大值是3588元. ----2分
23. (1)解:由题意可令y=0时,则有:
,解得: ,
∴点A、B的坐标分别为 、 ----3分
(2)解:由题意得: ,
∵当m≥0时,n 的取值范围是n≥-9,
∴顶点的纵坐标为-9,即 ,
∴ ,
∴抛物线的解析式为 ----3分
(3)解:当a=1时,则有: ,
设抛物线向上平移m(m>0)个单位长度得到新抛物线G的解析式为 ,
由(2)可知抛物线 的顶点坐标为 ,
∴当抛物线 向上平移9个单位长度时,此时抛物线G与x轴只有一个交点为 ,
∴m=9 ----2分
当抛物线G上的一个点为 时,即 ,
解得: ,
∴m 的取值范围为 ----2分
24.(本题12分)
解:(1)①证明:如图1,
∵BA=BO, ∴
∵BA⊥BC, ∴
而
∴
∵OB⊥OC,∴
∴
∴ ----3分
②如图2,分别过点A、B、C作AH⊥OB于点H,BM⊥OA于点M,CN⊥OA于点N,
由题意可知,
在Rt△AHO中,设AH=m,OH=3m.
∵,∴,解得m=4.
∴
∵∴,
∴,
∵ ∴
∴
∴
∴ ∴
∴. ----4分
(2)过点A作AH⊥OB于点H,则有AH=4,OH=12.
①如图3,当点C在第二象限内,时,设
又
,
,
∴整理得解得
②如图4,当点C在第二象限内, 时,
延长AB,CO交于点G,则,
又
而∠ABH=∠GBO,
③当点C在第四象限内,时,AC与OB相交于点E,则有
(a)如图5,点B在第三象限内.
在中,
又
而∠AEH=∠CEO,
(b)如图6,点B在第一象限内.
在中,
又
而∠AEH=∠CEO,
综上所述,OB的长为 ---- 每答对1个解给1分
同课章节目录
