8.3.2动能定理的应用(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理必修第二册(共31张PPT)
文档属性
| 名称 | 8.3.2动能定理的应用(课件)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理必修第二册(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-01 21:20:38 | ||
图片预览









文档简介
(共31张PPT)
人教版(2019)高中物理必修第二册
第八章 机械能守恒定律
8.3.2 动能定理的应用
授课人:扬帆起航
CONTENTS
01
知识回顾
02
动能定理求恒力做功
03
动能定理求变力做功
目录
01
知识回顾
第八章 机械能守恒定律
1.表达式:Ek=_______;
2.标矢性:动能是 量,只有 ,没有方向;
3.物体动能的变化量是指
动能
1.关于物体的动能,下列说法正确的是
A.物体的质量、速度不变,其动能一定不变
B.物体的动能不变,其速度一定不变
C.两个物体中,速度大的动能也大
D.某一过程中物体的速度变化越大,其动能的变化一定越大
√
标
大小
知识回顾
末动能减去初动能
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中 ;
2.表达式:W=_____________。
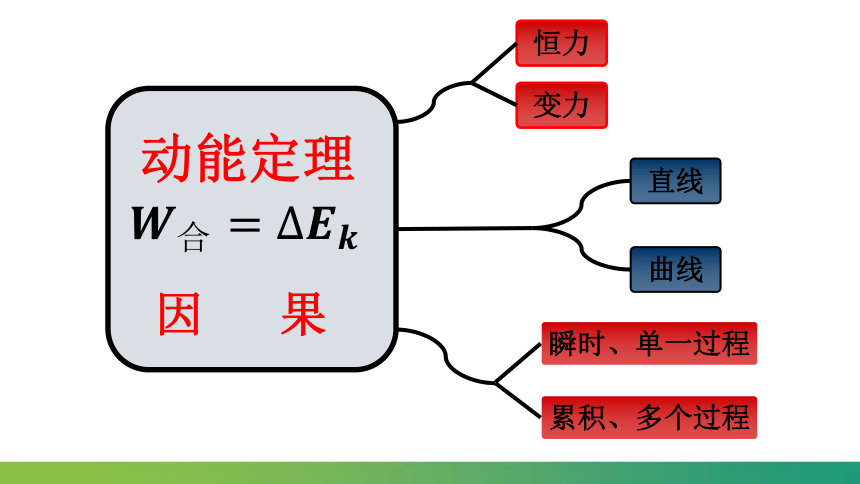
动能定理
动能的变化
知识回顾
W合= Ek2 -Ek1= ΔEk
动能定理
果
因
恒力
直线
曲线
变力
瞬时、单一过程
累积、多个过程
2. 一质量为1kg的物体被人用手由静止向上提升1m时,物体的速度为2m/s,取g=10m/s 2 ,下列说法正确的是
A.提升过程中手对物体做功 12J
B.提升过程中合外力对物体做功12J
C.提升过程中合外力对物体做功2J
D.提升过程中物体克服重力做功10J
解:由动能定理得
W合=
∴ W合 =2J
其中W合 =W手 +(- W克 )
∴ W手 =12J
物体克服重力做功W克 =mgh =10J
√
√
√
知识回顾
3.物体沿直线运动的v-t图象如图所示,已知在第1 s内合力对物体做功为W,则
A.从第1 s末到第3 s末合力做功为4W
B.从第3 s末到第5 s末合力做功为-2W
C.从第5 s末到第7 s末合力做功为W
D.从第3 s末到第4 s末合力做功为-0.5W
√
关键:
1.正确计算物体所受外力做的总功 ;
2.明确物体在运动过程中初、末状态的动能值。
【解题步骤】
总结:动能定理不涉及物理运动过程中的加速度和时间,而只与物体的初末状态有关。在处理物理问题时,应优先考虑应用动能定理。
(1)确定研究对象,通常是单个物体;
(3)分析物体的受力情况,明确各力做功的情况(做功的大小和正负),并确定外力所做的总功;
(4)明确初、末状态的动能,确定动能的变化ΔEk ;
(5)根据动能定理W总=Ek2 -Ek1列方程求解;
(2)明确运动过程,可以是某段过程,也可以是整个过程;
下抛
v0
平抛
v0
上抛
v0
h
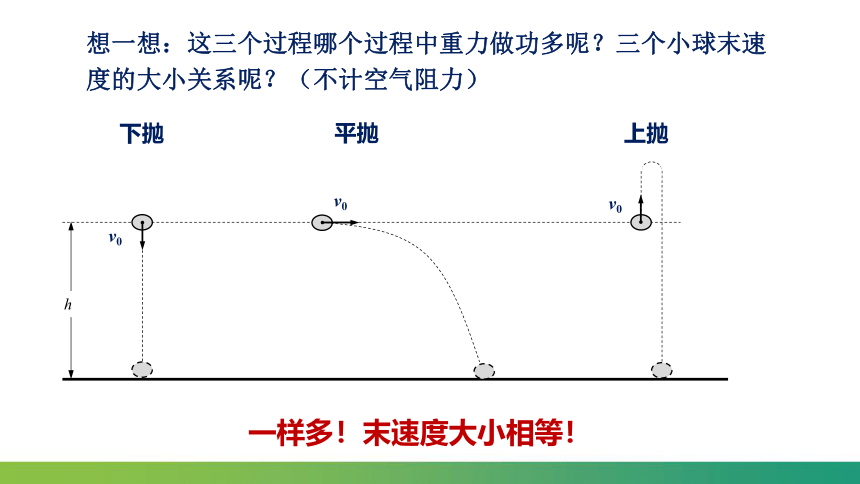
想一想:这三个过程哪个过程中重力做功多呢?三个小球末速度的大小关系呢?(不计空气阻力)
一样多!末速度大小相等!
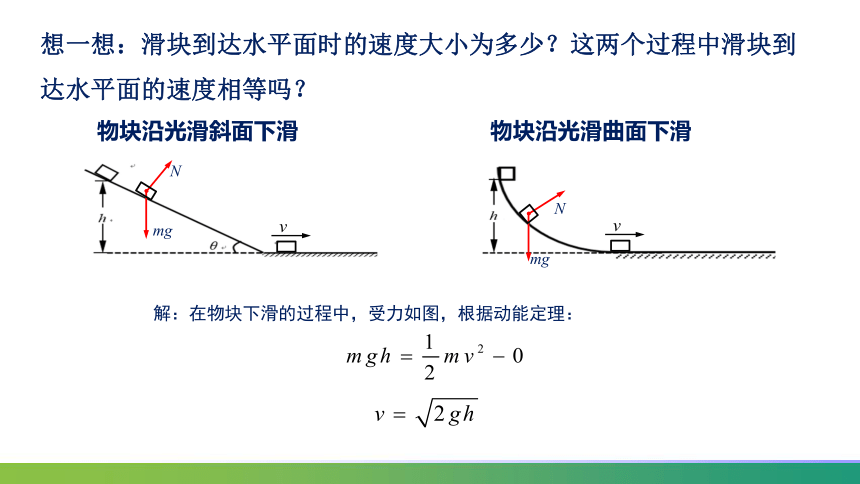
物块沿光滑曲面下滑
v
物块沿光滑斜面下滑
解:在物块下滑的过程中,受力如图,根据动能定理:
mg
N
mg
N
v
想一想:滑块到达水平面时的速度大小为多少?这两个过程中滑块到达水平面的速度相等吗?
02
动能定理求恒力做功
第八章 机械能守恒定律
一、利用动能定理求恒力做功
——恒力+直线
例1.一架喷气式飞机,质量m=5×103 kg,当起飞过程中从静止开始滑跑的路程为l=5.3×102m时,达到起飞速度v=60m/s,在此过程中飞机受到的平均阻力是飞机重量的k倍(k=0.02),求飞机受到的牵引力。
解:①常规方法
②动能定理法
例2.把质量为0.5kg的石块从10m高处以与水平方向抛出,初速度大小是v0=5m/s。(不计空气阻力)
(1)请求解石块落地时的速度大小。
解题思路:动能定理
解题思路:平抛运动
恒力做功问题
——恒力+曲线
变式:把质量为0.5kg的石块从10m高处以与水平方向成θ角斜向上抛出,初速度大小是v0=5m/s。(不计空气阻力)
(1)请求解石块落地时的速度大小。
问题:斜抛?
新思路:动能定理!
解:只有重力做功
恒力做功问题
——恒力+曲线
(2)石块落地时速度的大小与下列物理量有关( )
A.石块的质量
B.石块初速度的大小
C.石块初速度的仰角
D.石块抛出时的高度
答案:BD
恒力做功问题
——恒力+曲线
03
动能定理求变力做功
第八章 机械能守恒定律
例1. 质量为m的小球用长为L的轻绳悬挂于O点,小球在水平拉力F的作用下,从平衡位置P很缓慢地移到Q点,则力F所做的功为( )
A. mgLcos B. mgL(1 – cos )
C. FLsin D. FLcos
简析:球在F方向的位移s=Lsin
力F的功WF =Fs=F Lsin
很缓慢的含义:
可认为时刻静止
所受合力时刻为0
任意过程ΔEk= 0
由平衡条件得:F=mg tan ,故F为变力 , WF =F Lsin 错误
正确解答:本题中的变力功可由动能定理求解.
小球由P到Q,由动能定理得:WF + WG = 0
即WF – mgL(1 –cos )=0 ∴ WF = mgL(1 – cos )
B
F
P
Q
s
T
T
mg
二、利用动能定理求变力做功
例2. 质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一轻弹簧O端相距s,已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,重力加速度为g,则从开始碰撞到弹簧被压缩至最短,物体克服弹簧弹力所做的功为
√
变力做功问题
例3.有一半径为r=0.5 m的粗糙半圆轨道,A与圆心O等高,有一质量为m=0.2 kg的物块(可视为质点),从A点静止滑下,滑至最低点B时的速度为v=1 ,取 ,下列说法正确的是
A.物块过B点时,对轨道的压力大小是0.4 N
B.物块过B点时,对轨道的压力大小是2.0 N
C.A到B的过程中,克服摩擦力做的功为0.9 J
D.A到B的过程中,克服摩擦力做的功为0.1 J
√
解:在B点,由牛顿第二定律,FN-mg= FN=2.4 N,
由牛顿第三定律,物块对轨道的压力大小为2.4 N.
对于A 到B的过程,mgr+Wf= Wf=-0.9 J,克服摩擦力做功为0.9 J.
利用动能定理求变力的功
例4.质量为m 的物体静放在水平光滑的平台上,系在物体上的绳子跨过光滑的定滑轮由地面以速度v0向右匀速走动的人拉着,设人从地面上且从平台的边缘开始向右行至绳和水平方向成30°角处,在此过程中人所做的功为: ( )
A.
B.
C.
D.
√
点拨
当右段绳与水平夹角为θ时,沿着绳子方向的速率知绳子的拉力是变力,若直接用W=Fscosθ求功是不可能的,由动能定理可得:人所做的功等于物体动能的增量
即
故正确答案是D.
可见,用动能定理解决变力做功是一种常用方法,解此类问题关键是分清各力做功情况和初、末动能.
例5.一列货车的质量为5.0×105kg,在平直轨道以额定功率3000kw加速行驶,当速度由10m/s加速到所能达到的最大速度30m/s时,共用了2min,则这段时间内列车前进的距离是多少
F0
f
f 恒定
S=1600m
S
变力做功问题
——与机车启动相联系问题
例6、质量为m的汽车发动机的功率恒为P,摩擦阻力恒为f,牵引力为F.汽车由静止开始,经过时间t行驶了位移s时,速度达到最大值vm,则发动机所做的功为( )
D.
E.Fs
ABCD
注意:
做选择题时要注意表达式的多种可能性
A.Pt
C.
B.fvmt
解:A、根据功率的定义式p=w/t得
由于发动机的功率恒为P,所以发动机所做的功W发=pt,故A正确.
B、汽车启动达到最大速度时汽车的牵引力与阻力相等,根据功率的表达式p=Fv得:
W发=F牵vmt=Ffvmt,故B正确.
C、根据动能定理研究汽车由静止开始到最大速度的过程
W发+Wf=12mvm2
Wf=-Ffs
W发=12mvm2+Ffs 故C正确;
D、汽车启动达到最大速度时汽车的牵引力与阻力相等,所以vm=pF牵=pFf
Ff=pvm 所以W发=所以D正确.
E、整个F是变化的,所以牵引力的功不能用Fs表示,故E错误
故选:ABCD.
例7、运动员踢球的平均作用力为200N,把一个静止的质量为1kg的球以10m/s的速度踢出,水平面上运动60m后停下,则运动员对球做的功 如果运动员踢球时球以10m/s迎面飞来,踢出速度仍为10m/s,则运动员对球做的功为多少
F
S=60m
vo
v=0
变力做功问题
——瞬间力做功问题
例8.某人从距地面25m高处斜上抛出一小球,小球质量100g,出手时速度大小为10m/s,落地时速度大小为16m/s,取g=10m/s2,试求:
(1)人抛球时对小球做多少功?
(2)小球在空中运动时克服阻力做功多少?
V0
H
V
解:(1)人抛球:
(2)球在空中:
注意:列式时要注意W合和△Ek的正负
代入数据解得
所以克服阻力做了17.2J的功
1. 通常情况下,若问题涉及时间、加速度或过程的细节,要用牛顿运动定律解决;而曲线运动、变力做功等问题,一般要用动能定理解决。即使是恒力,当不涉及加速度和时间,并且是两个状态点的速度比较明确的情况,也应优先考虑动能定理。
2. 利用动能定理求变力的功是最常用的方法,当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W变+W其他=ΔEk.
利用动能定理求变力的功
人教版(2019)高中物理必修第二册
第八章 机械能守恒定律
8.3.2 动能定理的应用
授课人:扬帆起航
CONTENTS
01
知识回顾
02
动能定理求恒力做功
03
动能定理求变力做功
目录
01
知识回顾
第八章 机械能守恒定律
1.表达式:Ek=_______;
2.标矢性:动能是 量,只有 ,没有方向;
3.物体动能的变化量是指
动能
1.关于物体的动能,下列说法正确的是
A.物体的质量、速度不变,其动能一定不变
B.物体的动能不变,其速度一定不变
C.两个物体中,速度大的动能也大
D.某一过程中物体的速度变化越大,其动能的变化一定越大
√
标
大小
知识回顾
末动能减去初动能
1.内容:力在一个过程中对物体做的功,等于物体在这个过程中 ;
2.表达式:W=_____________。
动能定理
动能的变化
知识回顾
W合= Ek2 -Ek1= ΔEk
动能定理
果
因
恒力
直线
曲线
变力
瞬时、单一过程
累积、多个过程
2. 一质量为1kg的物体被人用手由静止向上提升1m时,物体的速度为2m/s,取g=10m/s 2 ,下列说法正确的是
A.提升过程中手对物体做功 12J
B.提升过程中合外力对物体做功12J
C.提升过程中合外力对物体做功2J
D.提升过程中物体克服重力做功10J
解:由动能定理得
W合=
∴ W合 =2J
其中W合 =W手 +(- W克 )
∴ W手 =12J
物体克服重力做功W克 =mgh =10J
√
√
√
知识回顾
3.物体沿直线运动的v-t图象如图所示,已知在第1 s内合力对物体做功为W,则
A.从第1 s末到第3 s末合力做功为4W
B.从第3 s末到第5 s末合力做功为-2W
C.从第5 s末到第7 s末合力做功为W
D.从第3 s末到第4 s末合力做功为-0.5W
√
关键:
1.正确计算物体所受外力做的总功 ;
2.明确物体在运动过程中初、末状态的动能值。
【解题步骤】
总结:动能定理不涉及物理运动过程中的加速度和时间,而只与物体的初末状态有关。在处理物理问题时,应优先考虑应用动能定理。
(1)确定研究对象,通常是单个物体;
(3)分析物体的受力情况,明确各力做功的情况(做功的大小和正负),并确定外力所做的总功;
(4)明确初、末状态的动能,确定动能的变化ΔEk ;
(5)根据动能定理W总=Ek2 -Ek1列方程求解;
(2)明确运动过程,可以是某段过程,也可以是整个过程;
下抛
v0
平抛
v0
上抛
v0
h
想一想:这三个过程哪个过程中重力做功多呢?三个小球末速度的大小关系呢?(不计空气阻力)
一样多!末速度大小相等!
物块沿光滑曲面下滑
v
物块沿光滑斜面下滑
解:在物块下滑的过程中,受力如图,根据动能定理:
mg
N
mg
N
v
想一想:滑块到达水平面时的速度大小为多少?这两个过程中滑块到达水平面的速度相等吗?
02
动能定理求恒力做功
第八章 机械能守恒定律
一、利用动能定理求恒力做功
——恒力+直线
例1.一架喷气式飞机,质量m=5×103 kg,当起飞过程中从静止开始滑跑的路程为l=5.3×102m时,达到起飞速度v=60m/s,在此过程中飞机受到的平均阻力是飞机重量的k倍(k=0.02),求飞机受到的牵引力。
解:①常规方法
②动能定理法
例2.把质量为0.5kg的石块从10m高处以与水平方向抛出,初速度大小是v0=5m/s。(不计空气阻力)
(1)请求解石块落地时的速度大小。
解题思路:动能定理
解题思路:平抛运动
恒力做功问题
——恒力+曲线
变式:把质量为0.5kg的石块从10m高处以与水平方向成θ角斜向上抛出,初速度大小是v0=5m/s。(不计空气阻力)
(1)请求解石块落地时的速度大小。
问题:斜抛?
新思路:动能定理!
解:只有重力做功
恒力做功问题
——恒力+曲线
(2)石块落地时速度的大小与下列物理量有关( )
A.石块的质量
B.石块初速度的大小
C.石块初速度的仰角
D.石块抛出时的高度
答案:BD
恒力做功问题
——恒力+曲线
03
动能定理求变力做功
第八章 机械能守恒定律
例1. 质量为m的小球用长为L的轻绳悬挂于O点,小球在水平拉力F的作用下,从平衡位置P很缓慢地移到Q点,则力F所做的功为( )
A. mgLcos B. mgL(1 – cos )
C. FLsin D. FLcos
简析:球在F方向的位移s=Lsin
力F的功WF =Fs=F Lsin
很缓慢的含义:
可认为时刻静止
所受合力时刻为0
任意过程ΔEk= 0
由平衡条件得:F=mg tan ,故F为变力 , WF =F Lsin 错误
正确解答:本题中的变力功可由动能定理求解.
小球由P到Q,由动能定理得:WF + WG = 0
即WF – mgL(1 –cos )=0 ∴ WF = mgL(1 – cos )
B
F
P
Q
s
T
T
mg
二、利用动能定理求变力做功
例2. 质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一轻弹簧O端相距s,已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,重力加速度为g,则从开始碰撞到弹簧被压缩至最短,物体克服弹簧弹力所做的功为
√
变力做功问题
例3.有一半径为r=0.5 m的粗糙半圆轨道,A与圆心O等高,有一质量为m=0.2 kg的物块(可视为质点),从A点静止滑下,滑至最低点B时的速度为v=1 ,取 ,下列说法正确的是
A.物块过B点时,对轨道的压力大小是0.4 N
B.物块过B点时,对轨道的压力大小是2.0 N
C.A到B的过程中,克服摩擦力做的功为0.9 J
D.A到B的过程中,克服摩擦力做的功为0.1 J
√
解:在B点,由牛顿第二定律,FN-mg= FN=2.4 N,
由牛顿第三定律,物块对轨道的压力大小为2.4 N.
对于A 到B的过程,mgr+Wf= Wf=-0.9 J,克服摩擦力做功为0.9 J.
利用动能定理求变力的功
例4.质量为m 的物体静放在水平光滑的平台上,系在物体上的绳子跨过光滑的定滑轮由地面以速度v0向右匀速走动的人拉着,设人从地面上且从平台的边缘开始向右行至绳和水平方向成30°角处,在此过程中人所做的功为: ( )
A.
B.
C.
D.
√
点拨
当右段绳与水平夹角为θ时,沿着绳子方向的速率知绳子的拉力是变力,若直接用W=Fscosθ求功是不可能的,由动能定理可得:人所做的功等于物体动能的增量
即
故正确答案是D.
可见,用动能定理解决变力做功是一种常用方法,解此类问题关键是分清各力做功情况和初、末动能.
例5.一列货车的质量为5.0×105kg,在平直轨道以额定功率3000kw加速行驶,当速度由10m/s加速到所能达到的最大速度30m/s时,共用了2min,则这段时间内列车前进的距离是多少
F0
f
f 恒定
S=1600m
S
变力做功问题
——与机车启动相联系问题
例6、质量为m的汽车发动机的功率恒为P,摩擦阻力恒为f,牵引力为F.汽车由静止开始,经过时间t行驶了位移s时,速度达到最大值vm,则发动机所做的功为( )
D.
E.Fs
ABCD
注意:
做选择题时要注意表达式的多种可能性
A.Pt
C.
B.fvmt
解:A、根据功率的定义式p=w/t得
由于发动机的功率恒为P,所以发动机所做的功W发=pt,故A正确.
B、汽车启动达到最大速度时汽车的牵引力与阻力相等,根据功率的表达式p=Fv得:
W发=F牵vmt=Ffvmt,故B正确.
C、根据动能定理研究汽车由静止开始到最大速度的过程
W发+Wf=12mvm2
Wf=-Ffs
W发=12mvm2+Ffs 故C正确;
D、汽车启动达到最大速度时汽车的牵引力与阻力相等,所以vm=pF牵=pFf
Ff=pvm 所以W发=所以D正确.
E、整个F是变化的,所以牵引力的功不能用Fs表示,故E错误
故选:ABCD.
例7、运动员踢球的平均作用力为200N,把一个静止的质量为1kg的球以10m/s的速度踢出,水平面上运动60m后停下,则运动员对球做的功 如果运动员踢球时球以10m/s迎面飞来,踢出速度仍为10m/s,则运动员对球做的功为多少
F
S=60m
vo
v=0
变力做功问题
——瞬间力做功问题
例8.某人从距地面25m高处斜上抛出一小球,小球质量100g,出手时速度大小为10m/s,落地时速度大小为16m/s,取g=10m/s2,试求:
(1)人抛球时对小球做多少功?
(2)小球在空中运动时克服阻力做功多少?
V0
H
V
解:(1)人抛球:
(2)球在空中:
注意:列式时要注意W合和△Ek的正负
代入数据解得
所以克服阻力做了17.2J的功
1. 通常情况下,若问题涉及时间、加速度或过程的细节,要用牛顿运动定律解决;而曲线运动、变力做功等问题,一般要用动能定理解决。即使是恒力,当不涉及加速度和时间,并且是两个状态点的速度比较明确的情况,也应优先考虑动能定理。
2. 利用动能定理求变力的功是最常用的方法,当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W变+W其他=ΔEk.
利用动能定理求变力的功
