2022年强化训练冀教版八年级数学下册第二十一章一次函数同步训练试题(word版 含解析)
文档属性
| 名称 | 2022年强化训练冀教版八年级数学下册第二十一章一次函数同步训练试题(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 362.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 16:23:38 | ||
图片预览



文档简介
八年级数学下册第二十一章一次函数同步训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、一次函数的图象一定经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第二、三、四象限 D.第一、二、四象限
2、关于一次函数 ,下列说法不正确的是( )
A.图象经过点(2,0) B.图象经过第三象限
C.函数y随自变量x的增大而减小 D.当x≥2时,y≤0
3、若一次函数的图像经过第一、三、四象限,则的值可能为( )
A.-2 B.-1 C.0 D.2
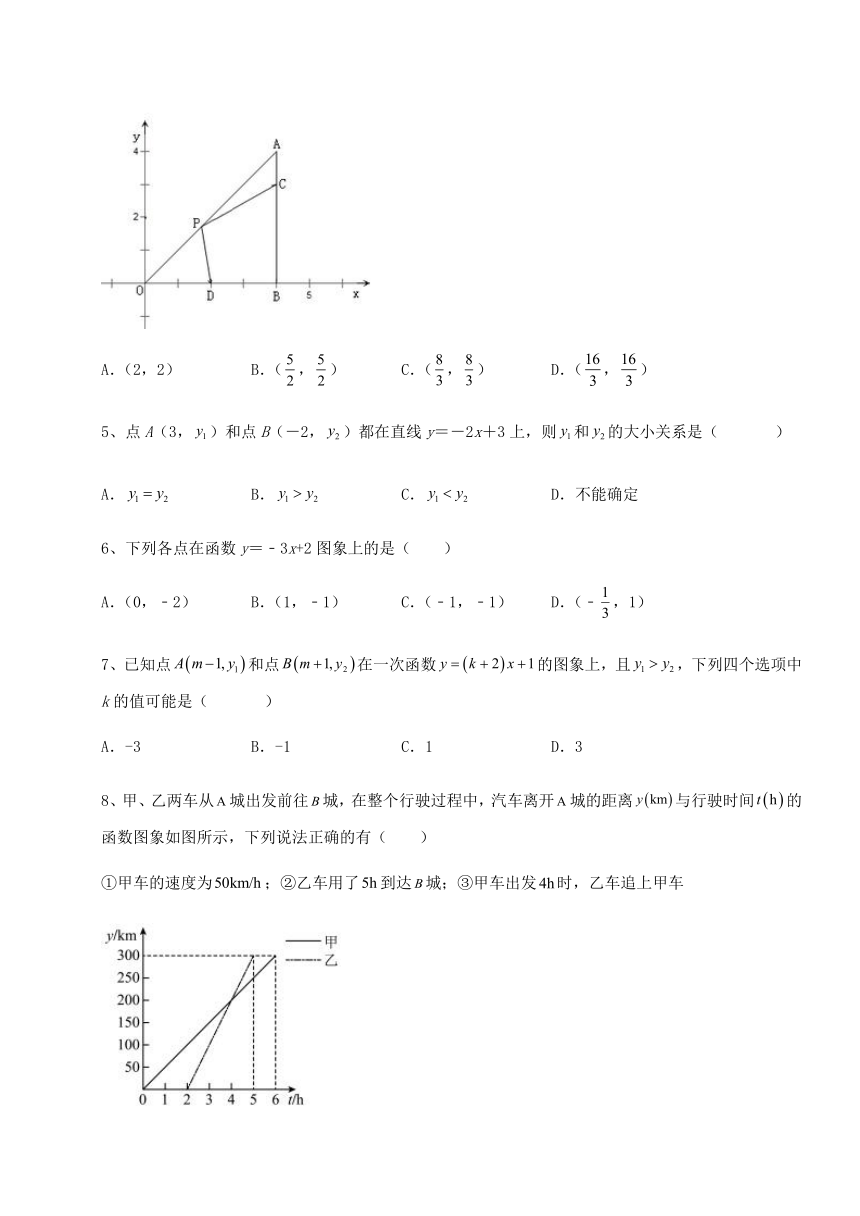
4、如图,在Rt△ABO中,∠OBA=90°,A(4,4),且,点D为OB的中点,点P为边OA上的动点,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2) B.(,) C.(,) D.(,)
5、点A(3,)和点B(-2,)都在直线y=-2x+3上,则和的大小关系是( )
A. B. C. D.不能确定
6、下列各点在函数y=﹣3x+2图象上的是( )
A.(0,﹣2) B.(1,﹣1) C.(﹣1,﹣1) D.(﹣,1)
7、已知点和点在一次函数的图象上,且,下列四个选项中k的值可能是( )
A.-3 B.-1 C.1 D.3
8、甲、乙两车从城出发前往城,在整个行驶过程中,汽车离开城的距离与行驶时间的函数图象如图所示,下列说法正确的有( )
①甲车的速度为;②乙车用了到达城;③甲车出发时,乙车追上甲车
A.0个 B.1个 C.2个 D.3个
9、如图,一次函数y=f(x)的图像经过点(2,0),如果y>0,那么对应的x的取值范围是( )
A.x<2 B.x>2 C.x<0 D.x>0
10、点和点都在直线上,则与的大小关系为( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、已知:直线与直线的图象交点如图所示,则方程组的解为______.
2、用待定系数法确定一次函数表达式所需要的步骤是什么?
①设——设函数表达式y=___,
②代——将点的坐标代入y=kx+b中,列出关于___、___的方程
③求——解方程,求k、b
④写——把求出的k、b值代回到表达式中即可.
3、将直线沿轴向上平移2个单位长度后的直线所对应的函数表达式是__________.
4、直线y1=-x+m和y2=2x+n的交点如图,则不等式-x+m<2x+n的解集是_____.
5、已知,,在x轴找一点P,使的值最小,则点P的坐标为_______.
三、解答题(5小题,每小题10分,共计50分)
1、肥西县祥源花世界管理委员会要添置办公桌椅A,B两种型号,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)直接写出A型桌椅每套 元,B型桌椅每套 元;
(2)若管理委员会需购买两种型号桌椅共20套,若需要A型桌椅不少于12套,B型桌椅不少于6套,平均每套桌椅需要运费10元.设购买A型桌椅x套,总费用为y元.
①求y与x之间的函数关系,并直接写出x的取值范围;
②求出总费用最少的购置方案.
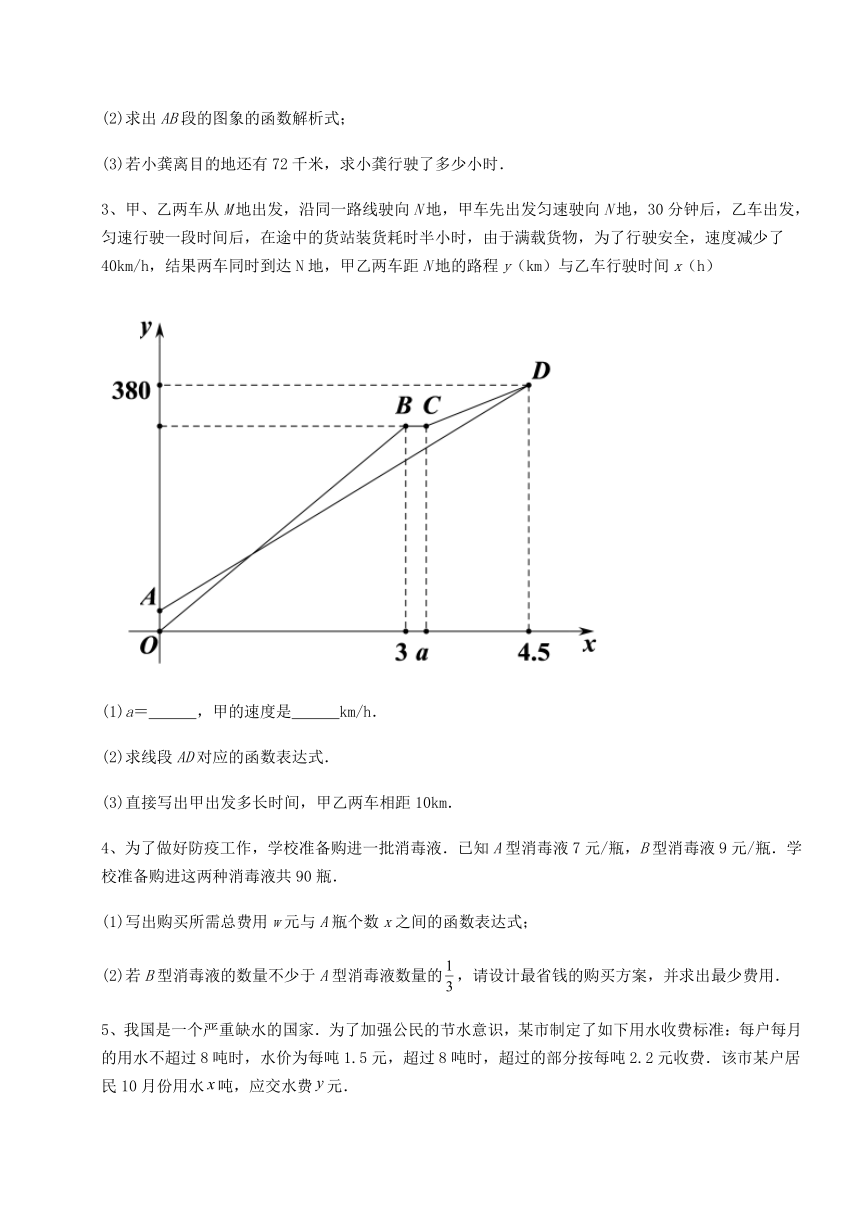
2、国庆期间,小龚自驾游去了离家156千米的月亮湾,如图是小龚离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小龚出发36分钟时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)若小龚离目的地还有72千米,求小龚行驶了多少小时.
3、甲、乙两车从M地出发,沿同一路线驶向N地,甲车先出发匀速驶向N地,30分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了40km/h,结果两车同时到达N地,甲乙两车距N地的路程y(km)与乙车行驶时间x(h)
(1)a= ,甲的速度是 km/h.
(2)求线段AD对应的函数表达式.
(3)直接写出甲出发多长时间,甲乙两车相距10km.
4、为了做好防疫工作,学校准备购进一批消毒液.已知A型消毒液7元/瓶,B型消毒液9元/瓶.学校准备购进这两种消毒液共90瓶.
(1)写出购买所需总费用w元与A瓶个数x之间的函数表达式;
(2)若B型消毒液的数量不少于A型消毒液数量的,请设计最省钱的购买方案,并求出最少费用.
5、我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水吨,应交水费元.
(1)若,请写出与的函数关系式.
(2)若,请写出与的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
-参考答案-
一、单选题
1、C
【解析】
【分析】
k<0,函数一定经过第二,四象限,b<0,直线与y轴交于负半轴,所以函数图象过第三象限.
【详解】
解:∵k=-2<0,b=-3<0,
∴函数的图象经过第二、三、四象限,
故选:C.
【点睛】
本题考查了一次函数的性质,k>0,函数一定经过第一,三象限,k<0,函数一定经过第二,四象限,再根据直线与y轴的交点即可得出函数所过的象限,这是解题的关键.
2、B
【解析】
【分析】
当 时, ,可得图象经过点(2,0);再由 ,可得图象经过第一、二、四象限;函数y随自变量x的增大而减小;然后根据 时, ,可得当x≥2时,y≤0,即可求解.
【详解】
解:当 时, ,
∴图象经过点(2,0),故A正确,不符合题意;
∵ ,
∴图象经过第一、二、四象限,故B错误,符合题意;
∴函数y随自变量x的增大而减小,故C正确,不符合题意;
当 时, ,
∴当x≥2时,y≤0,故D正确,不符合题意;
故选:B
【点睛】
本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.
3、D
【解析】
【分析】
利用一次函数图象与系数的关系可得出m-1>0,解之即可得出m的取值范围,再对照四个选项即可得出结论.
【详解】
解:∵一次函数y=(m-1)x-1的图象经过第一、三、四象限,
∴m-1>0,
∴m>1,
∴m的值可能为2.
故选:D.
【点睛】
本题考查了一次函数图象与系数的关系、解一元一次不等式,牢记“k>0,b<0 y=kx+b的图象经过一、三、四象限”是解题的关键.
4、C
【解析】
【分析】
先确定点D关于直线AO的对称点E(0,2),确定直线CE的解析式,直线AO的解析式,两个解析式的交点就是所求.
【详解】
∵∠OBA=90°,A(4,4),且,点D为OB的中点,
∴点D(2,0),AC=1,BC=3,点C(4,3),
设直线AO的解析式为y=kx,
∴4=4k,
解得k=1,
∴直线AO的解析式为y=x,
过点D作DE⊥AO,交y轴于点E,交AO于点F,
∵∠OBA=90°,A(4,4),
∴∠AOE=∠AOB=45°,
∴∠OED=∠ODE=45°,OE=OD,
∴DF=FE,
∴点E是点D关于直线AO的对称点,
∴点E(0,2),
连接CE,交AO于点P,此时,点P是四边形PCBD周长最小的位置,
设CE的解析式为y=mx+n,
∴,
解得,
∴直线CE的解析式为y=x+2,
∴,
解得,
∴使四边形PDBC周长最小的点P的坐标为(,),
故选C.
【点睛】
本题考查了一次函数的解析式,将军饮马河原理,熟练掌握待定系数法和将军饮马河原理是解题的关键.
5、C
【解析】
【分析】
利用一次函数的增减性性质判定即可.
【详解】
∵直线y=-2x+3的k=-2<0,
∴y随x的增大而减小,
∵-2<3,
∴,
故选C.
【点睛】
本题考查了一次函数的增减性,熟练掌握性质是解题的关键.
6、B
【解析】
【分析】
根据一次函数图象上点的坐标满足函数解析式,逐一判断,即可得到答案.
【详解】
∵,
∴A不符合题意,
∵,
∴B符合题意,
∵,
∴C不符合题意,
∵,
∴D不符合题意,
故选B.
【点睛】
本题主要考查一次函数图象上点的坐标,掌握一次函数图象上点的坐标满足函数解析式,是解题的关键.
7、A
【解析】
【分析】
由m-1<m+1时,y1>y2,可知y随x增大而减小,则比例系数k+2<0,从而求出k的取值范围.
【详解】
解:当m-1<m+1时,y1>y2,y随x的增大而减小,
∴k+2<0,得k<﹣2.
故选:A.
【点睛】
本题考查一次函数的图象性质:当k<0,y随x增大而减小,难度不大.
8、C
【解析】
【分析】
求出正比函数的解析式,k值的绝对值表示车的速度;横轴上两个时间点的差表示乙走完全程所用时间,求出一次函数的解析式,确定它与正比例函数的交点坐标,横坐标即为二车相遇时间.
【详解】
设甲的解析式为y=kx,
∴6k=300,
解得k=50,
∴=50x,
∴甲车的速度为,
∴①正确;
∵乙晚出发2小时,
∴乙车用了5-2=3(h)到达城,
∴②错误;
设,
∴,
∴,
∴,
∵,
∴,
即甲行驶4小时,乙追上甲,
∴③正确;
故选C.
【点睛】
本题考查了待定系数法确定函数的解析式,函数图像,交点坐标的确定,解二元一次方程组,熟练掌握待定系数法,准确求交点的坐标是解题的关键.
9、A
【解析】
【分析】
y>0即是图象在x轴上方,找出这部分图象上点对应的横坐标范围即可.
【详解】
解:∵一次函数y=f(x)的图象经过点(2,0),
∴如果y>0,则x<2,
故选:A.
【点睛】
本题考查一次函数的图象,数形结合是解题的关键.
10、B
【解析】
【分析】
根据 ,可得 随 的增大而减小,即可求解.
【详解】
解:∵ ,
∴ 随 的增大而减小,
∵ ,
∴ .
故选:B
【点睛】
本题主要考查了一次函数的性质,熟练掌握对于一次函数 ,当 时, 随 的增大而增大,当 时, 随 的增大而减小是解题的关键.
二、填空题
1、
【解析】
【分析】
根据函数图象与二元一次方程组的关系,求方程组的解,就是求两方程所表示的两一次函数图象交点的坐标,从而得出答案.
【详解】
解:∵函数y=x-b与函数y=mx+6的交点坐标是(2,3),
∴方程组的解为.
故答案为.
【点睛】
本题主要考查了一次函数与二元一次方程组的关系,比较简单,熟悉交点坐标就是方程组的解是解题的关键.
2、 kx+b k b
【解析】
略
3、
【解析】
【分析】
根据一次函数的平移规律:“上加下减常数项,左加右减自变量”,可知将函数沿着y轴向上平移2个单位长度,就是给原一次函数常数项后加2,化简后即可得到答案.
【详解】
根据一次函数的平移规律:“上加下减常数项,左加右减自变量”,可知将函数沿着y轴向上平移2个单位长度,就是给原一次函数常数项后加2,则变化后的函数解析式应变为:,化简后结果为: ,
故答案为:.
【点睛】
本题考查一次函数的图像变化与函数解析式变化之间的规律,熟练掌握并应用变化规律是解决本题的关键.
4、x<1
【解析】
略
5、
【解析】
【分析】
根据题意求出A点关于y轴的对称点,连接,交x轴于点P,则P即为所求点,用待定系数法求出过两点的直线解析式,求出此解析式与x轴的交点坐标即可.
【详解】
解:作点A关于y轴的对称点,连接,
设过的直线解析式为,把,,
则
解得:,,
故此直线的解析式为:,
当时,,
即点P的坐标为.
故答案为:.
【点睛】
本题考查的是最短线路问题及用待定系数法求一次函数的解析式,熟知轴对称的性质及一次函数的相关知识是解答此题的关键.
三、解答题
1、 (1)A型桌椅每套600元,B型桌椅每套800元;
(2)购买A型桌椅14套、B型桌椅6套,总费用最少,最少总费用为13400元
【解析】
【分析】
(1)设A型桌椅每套a元,B型桌椅每套b元,根据题意列二元一次方程组并解方程即可;
(2)①根据总费用=A型桌椅的费用+B型桌椅的费用建立y与x之间的函数关系式子,再由A型桌椅不少于12套,B型桌椅不少于6套列出一元一次不等式组求解即可得出x的取值范围;
②根据一次函数的性质求解即可.
(1)
解:设A型桌椅每套a元,B型桌椅每套b元,
根据题意,得:,
解得:,
所以A型桌椅每套600元,B型桌椅每套800元;
(2)
解:①据题意,总费用y=600x+800(20-x)+20×10=-200x+16200,
∵A型桌椅不少于12套,B型桌椅不少于6套,
∴,解得:12≤x≤14,
所以y与x之间的函数关系为y=-200x+16200(12≤x≤14,x为整数);
②由①知y=-200x+16200,且-200<0,
∴y随x的增大而减小,
∴当x=14时,总费用y最少,最少费用为-200×14+16200=13400元,
即购买A型桌椅14套、B型桌椅6套,总费用最少,最少总费用为13400元.
【点睛】
本题考查二元一次方程的应用、一次函数的应用、一元一次不等式组的应用,理解题意,正确列出方程或函数关系式是解答的关键.
2、 (1)36千米
(2)y=90x-24 (0.8≤x≤2)
(3)1.2小时
【解析】
【分析】
(1)由OA段可求得此时小龚驾车的速度,从而可求得36分钟离家的距离;
(2)用待定系数法.AB段过点A与B,把这两点的坐标代入所设函数解析式中即可求得函数解析式;
(3)由题意可得小龚离家的距离,根据(2)中求得的函数解析式的函数值,解方程即可求得x的值,从而求得小龚行驶的时间.
(1)
在OA段,小龚行驶的速度为:48÷0.8=60(千米/时),36分钟=0.6小时,则小龚出发36分钟时,离家的距离为60×0.6=36(千米);
(2)
由图象知: ,
设AB段的函数解析式为:
把A、B两点的坐标分别代入上式得:
解得:
∴AB段的函数解析式为(0.8≤x≤2)
(3)
由图象知,当小龚离目的地还有72千米时,他已行驶了156 72=84(千米)
所以在中,当y=84时,即,得
即小龚离目的地还有72千米,小龚行驶了1.2小时.
【点睛】
本题考查了一次函数(正比例函数)的图象与性质,待定系数法求函数解析式,已知函数值求自变量的值等知识,数形结合是本题的关键.
3、 (1)3.5小时,76;
(2)线段AD对应的函数表达式为.
(3)甲出发或或或小时,甲乙两车相距10km.
【解析】
【分析】
(1)根据乙车3小时到货站,在货站装货耗时半小时,得出小时,甲提前30分钟,可求甲车行驶的时间为:0.5+4.5=5小时,然后甲车速度=千米/时即可;
(2)利用待定系数法AD解析式为:,把AD两点坐标代入解析式得解方程即可;
(3)分两种情况,甲出发,乙未出发76t=10,乙出发后,设乙车的速度为xkm/h,利用行程列方程3x+(x-40)×1=380解方程求出x=105km/h,再用待定系数法,列方程,CD段乙车速度为105-40=65km/h,求出CD的解析式为,列方程,结合甲先行30分根据有理数加法求出甲所用时间即可.
(1)
解:∵3小时到货站,在货站装货耗时半小时,
∴小时,
甲车行驶的时间为:0.5+4.5=5小时,
甲车速度=千米/时,
故答案为:3.5小时,76;
(2)
点A表示的路程为:76×0.5=38,
设AD解析式为:,把AD两点坐标代入解析式得:
,
解得:,
线段AD对应的函数表达式为.
(3)
甲出发乙未出发,
∴76t=10,
∴t=,
乙出发后;
设乙车的速度为vkm/h,
3v+(v-40)×1=380
解得v=105km/h,
∴点B(3,315)
设OB解析式为,代入坐标得:,
∴OB解析式为
∴,
化简为:或,
解得或,
∵CD段乙车速度为105-40=65km/h,
设CD的解析式为代入点D坐标得,
,
解得:,
∴CD的解析式为,
∴,
解得:,
∵甲提前出发30分钟,
,,,
甲出发或或或小时,甲乙两车相距10km.
【点睛】
本题考查待定系数法求一次函数解析式,利用函数图像获取信息,绝对值方程,一元一次方程,二元一次方程组解法,分类讨论思想的应用使问题完整解决是解题关键.
4、 (1)w=-2x+810
(2)最省钱的购买方案是购进A型消毒液67瓶,购进B型消毒液23瓶,最低费用为676元
【解析】
【分析】
(1)A瓶个数为x,则B瓶个数为(90-x),根据题意列式计算即可;
(2)根据B型消毒液的数量不少于A型消毒液数量的,可以得到A型消毒液数量的取值范围,再根据一次函数的性质,即可求得最省钱的购买方案,计算出最少费用.
(1)
解:A瓶个数为x,则B瓶个数为(90-x),
依题意可得:w=7x+9(90-x)=-2x+810;
(2)
解:∵B型消毒液的数量不少于A型消毒液数量的,
∴,解得,
由(1)知w=﹣2x+810,
∴w随x的增大而减小,
∴当x=67时,w取得最小值,
此时w=﹣2×67+810=676,90﹣x=23,
答:最省钱的购买方案是购进A型消毒液67瓶,购进B型消毒液23瓶,最低费用为676元.
【点睛】
本题考查了一次函数的应用、二元一次方程组的应用、一元一次不等式的应用,解答本题的关键是列出相应的方程组和列出相应的函数关系式,利用一次函数的性质和不等式的性质解答.
5、 (1)
(2)
(3)13吨
【解析】
【分析】
(1)当0<x≤8时,根据水费=用水量×1.5,即可求出y与x的函数关系式;
(2)当x>8时,根据“每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费”,得出水费=8×1.5+(用水量-8)×2.2,即可求出y与x的函数关系式;
(3)当0<x≤8时,y≤12,由此可知这个月该户用水量超过8吨,将y=23代入(2)中所求的关系式,求出x的值即可.
(1)
根据题意可知:
当时,;
(2)
根据题意可知:
当时,;
(3)
当时,,
的最大值为(元,,
该户当月用水超过8吨.
令中,则,
解得:.
答:这个月该户用了13吨水.
【点睛】
本题考查了一次函数的应用,根据数量关系找出函数关系式是解题关键.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、一次函数的图象一定经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第二、三、四象限 D.第一、二、四象限
2、关于一次函数 ,下列说法不正确的是( )
A.图象经过点(2,0) B.图象经过第三象限
C.函数y随自变量x的增大而减小 D.当x≥2时,y≤0
3、若一次函数的图像经过第一、三、四象限,则的值可能为( )
A.-2 B.-1 C.0 D.2
4、如图,在Rt△ABO中,∠OBA=90°,A(4,4),且,点D为OB的中点,点P为边OA上的动点,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2) B.(,) C.(,) D.(,)
5、点A(3,)和点B(-2,)都在直线y=-2x+3上,则和的大小关系是( )
A. B. C. D.不能确定
6、下列各点在函数y=﹣3x+2图象上的是( )
A.(0,﹣2) B.(1,﹣1) C.(﹣1,﹣1) D.(﹣,1)
7、已知点和点在一次函数的图象上,且,下列四个选项中k的值可能是( )
A.-3 B.-1 C.1 D.3
8、甲、乙两车从城出发前往城,在整个行驶过程中,汽车离开城的距离与行驶时间的函数图象如图所示,下列说法正确的有( )
①甲车的速度为;②乙车用了到达城;③甲车出发时,乙车追上甲车
A.0个 B.1个 C.2个 D.3个
9、如图,一次函数y=f(x)的图像经过点(2,0),如果y>0,那么对应的x的取值范围是( )
A.x<2 B.x>2 C.x<0 D.x>0
10、点和点都在直线上,则与的大小关系为( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、已知:直线与直线的图象交点如图所示,则方程组的解为______.
2、用待定系数法确定一次函数表达式所需要的步骤是什么?
①设——设函数表达式y=___,
②代——将点的坐标代入y=kx+b中,列出关于___、___的方程
③求——解方程,求k、b
④写——把求出的k、b值代回到表达式中即可.
3、将直线沿轴向上平移2个单位长度后的直线所对应的函数表达式是__________.
4、直线y1=-x+m和y2=2x+n的交点如图,则不等式-x+m<2x+n的解集是_____.
5、已知,,在x轴找一点P,使的值最小,则点P的坐标为_______.
三、解答题(5小题,每小题10分,共计50分)
1、肥西县祥源花世界管理委员会要添置办公桌椅A,B两种型号,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)直接写出A型桌椅每套 元,B型桌椅每套 元;
(2)若管理委员会需购买两种型号桌椅共20套,若需要A型桌椅不少于12套,B型桌椅不少于6套,平均每套桌椅需要运费10元.设购买A型桌椅x套,总费用为y元.
①求y与x之间的函数关系,并直接写出x的取值范围;
②求出总费用最少的购置方案.
2、国庆期间,小龚自驾游去了离家156千米的月亮湾,如图是小龚离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小龚出发36分钟时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)若小龚离目的地还有72千米,求小龚行驶了多少小时.
3、甲、乙两车从M地出发,沿同一路线驶向N地,甲车先出发匀速驶向N地,30分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了40km/h,结果两车同时到达N地,甲乙两车距N地的路程y(km)与乙车行驶时间x(h)
(1)a= ,甲的速度是 km/h.
(2)求线段AD对应的函数表达式.
(3)直接写出甲出发多长时间,甲乙两车相距10km.
4、为了做好防疫工作,学校准备购进一批消毒液.已知A型消毒液7元/瓶,B型消毒液9元/瓶.学校准备购进这两种消毒液共90瓶.
(1)写出购买所需总费用w元与A瓶个数x之间的函数表达式;
(2)若B型消毒液的数量不少于A型消毒液数量的,请设计最省钱的购买方案,并求出最少费用.
5、我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水吨,应交水费元.
(1)若,请写出与的函数关系式.
(2)若,请写出与的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
-参考答案-
一、单选题
1、C
【解析】
【分析】
k<0,函数一定经过第二,四象限,b<0,直线与y轴交于负半轴,所以函数图象过第三象限.
【详解】
解:∵k=-2<0,b=-3<0,
∴函数的图象经过第二、三、四象限,
故选:C.
【点睛】
本题考查了一次函数的性质,k>0,函数一定经过第一,三象限,k<0,函数一定经过第二,四象限,再根据直线与y轴的交点即可得出函数所过的象限,这是解题的关键.
2、B
【解析】
【分析】
当 时, ,可得图象经过点(2,0);再由 ,可得图象经过第一、二、四象限;函数y随自变量x的增大而减小;然后根据 时, ,可得当x≥2时,y≤0,即可求解.
【详解】
解:当 时, ,
∴图象经过点(2,0),故A正确,不符合题意;
∵ ,
∴图象经过第一、二、四象限,故B错误,符合题意;
∴函数y随自变量x的增大而减小,故C正确,不符合题意;
当 时, ,
∴当x≥2时,y≤0,故D正确,不符合题意;
故选:B
【点睛】
本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.
3、D
【解析】
【分析】
利用一次函数图象与系数的关系可得出m-1>0,解之即可得出m的取值范围,再对照四个选项即可得出结论.
【详解】
解:∵一次函数y=(m-1)x-1的图象经过第一、三、四象限,
∴m-1>0,
∴m>1,
∴m的值可能为2.
故选:D.
【点睛】
本题考查了一次函数图象与系数的关系、解一元一次不等式,牢记“k>0,b<0 y=kx+b的图象经过一、三、四象限”是解题的关键.
4、C
【解析】
【分析】
先确定点D关于直线AO的对称点E(0,2),确定直线CE的解析式,直线AO的解析式,两个解析式的交点就是所求.
【详解】
∵∠OBA=90°,A(4,4),且,点D为OB的中点,
∴点D(2,0),AC=1,BC=3,点C(4,3),
设直线AO的解析式为y=kx,
∴4=4k,
解得k=1,
∴直线AO的解析式为y=x,
过点D作DE⊥AO,交y轴于点E,交AO于点F,
∵∠OBA=90°,A(4,4),
∴∠AOE=∠AOB=45°,
∴∠OED=∠ODE=45°,OE=OD,
∴DF=FE,
∴点E是点D关于直线AO的对称点,
∴点E(0,2),
连接CE,交AO于点P,此时,点P是四边形PCBD周长最小的位置,
设CE的解析式为y=mx+n,
∴,
解得,
∴直线CE的解析式为y=x+2,
∴,
解得,
∴使四边形PDBC周长最小的点P的坐标为(,),
故选C.
【点睛】
本题考查了一次函数的解析式,将军饮马河原理,熟练掌握待定系数法和将军饮马河原理是解题的关键.
5、C
【解析】
【分析】
利用一次函数的增减性性质判定即可.
【详解】
∵直线y=-2x+3的k=-2<0,
∴y随x的增大而减小,
∵-2<3,
∴,
故选C.
【点睛】
本题考查了一次函数的增减性,熟练掌握性质是解题的关键.
6、B
【解析】
【分析】
根据一次函数图象上点的坐标满足函数解析式,逐一判断,即可得到答案.
【详解】
∵,
∴A不符合题意,
∵,
∴B符合题意,
∵,
∴C不符合题意,
∵,
∴D不符合题意,
故选B.
【点睛】
本题主要考查一次函数图象上点的坐标,掌握一次函数图象上点的坐标满足函数解析式,是解题的关键.
7、A
【解析】
【分析】
由m-1<m+1时,y1>y2,可知y随x增大而减小,则比例系数k+2<0,从而求出k的取值范围.
【详解】
解:当m-1<m+1时,y1>y2,y随x的增大而减小,
∴k+2<0,得k<﹣2.
故选:A.
【点睛】
本题考查一次函数的图象性质:当k<0,y随x增大而减小,难度不大.
8、C
【解析】
【分析】
求出正比函数的解析式,k值的绝对值表示车的速度;横轴上两个时间点的差表示乙走完全程所用时间,求出一次函数的解析式,确定它与正比例函数的交点坐标,横坐标即为二车相遇时间.
【详解】
设甲的解析式为y=kx,
∴6k=300,
解得k=50,
∴=50x,
∴甲车的速度为,
∴①正确;
∵乙晚出发2小时,
∴乙车用了5-2=3(h)到达城,
∴②错误;
设,
∴,
∴,
∴,
∵,
∴,
即甲行驶4小时,乙追上甲,
∴③正确;
故选C.
【点睛】
本题考查了待定系数法确定函数的解析式,函数图像,交点坐标的确定,解二元一次方程组,熟练掌握待定系数法,准确求交点的坐标是解题的关键.
9、A
【解析】
【分析】
y>0即是图象在x轴上方,找出这部分图象上点对应的横坐标范围即可.
【详解】
解:∵一次函数y=f(x)的图象经过点(2,0),
∴如果y>0,则x<2,
故选:A.
【点睛】
本题考查一次函数的图象,数形结合是解题的关键.
10、B
【解析】
【分析】
根据 ,可得 随 的增大而减小,即可求解.
【详解】
解:∵ ,
∴ 随 的增大而减小,
∵ ,
∴ .
故选:B
【点睛】
本题主要考查了一次函数的性质,熟练掌握对于一次函数 ,当 时, 随 的增大而增大,当 时, 随 的增大而减小是解题的关键.
二、填空题
1、
【解析】
【分析】
根据函数图象与二元一次方程组的关系,求方程组的解,就是求两方程所表示的两一次函数图象交点的坐标,从而得出答案.
【详解】
解:∵函数y=x-b与函数y=mx+6的交点坐标是(2,3),
∴方程组的解为.
故答案为.
【点睛】
本题主要考查了一次函数与二元一次方程组的关系,比较简单,熟悉交点坐标就是方程组的解是解题的关键.
2、 kx+b k b
【解析】
略
3、
【解析】
【分析】
根据一次函数的平移规律:“上加下减常数项,左加右减自变量”,可知将函数沿着y轴向上平移2个单位长度,就是给原一次函数常数项后加2,化简后即可得到答案.
【详解】
根据一次函数的平移规律:“上加下减常数项,左加右减自变量”,可知将函数沿着y轴向上平移2个单位长度,就是给原一次函数常数项后加2,则变化后的函数解析式应变为:,化简后结果为: ,
故答案为:.
【点睛】
本题考查一次函数的图像变化与函数解析式变化之间的规律,熟练掌握并应用变化规律是解决本题的关键.
4、x<1
【解析】
略
5、
【解析】
【分析】
根据题意求出A点关于y轴的对称点,连接,交x轴于点P,则P即为所求点,用待定系数法求出过两点的直线解析式,求出此解析式与x轴的交点坐标即可.
【详解】
解:作点A关于y轴的对称点,连接,
设过的直线解析式为,把,,
则
解得:,,
故此直线的解析式为:,
当时,,
即点P的坐标为.
故答案为:.
【点睛】
本题考查的是最短线路问题及用待定系数法求一次函数的解析式,熟知轴对称的性质及一次函数的相关知识是解答此题的关键.
三、解答题
1、 (1)A型桌椅每套600元,B型桌椅每套800元;
(2)购买A型桌椅14套、B型桌椅6套,总费用最少,最少总费用为13400元
【解析】
【分析】
(1)设A型桌椅每套a元,B型桌椅每套b元,根据题意列二元一次方程组并解方程即可;
(2)①根据总费用=A型桌椅的费用+B型桌椅的费用建立y与x之间的函数关系式子,再由A型桌椅不少于12套,B型桌椅不少于6套列出一元一次不等式组求解即可得出x的取值范围;
②根据一次函数的性质求解即可.
(1)
解:设A型桌椅每套a元,B型桌椅每套b元,
根据题意,得:,
解得:,
所以A型桌椅每套600元,B型桌椅每套800元;
(2)
解:①据题意,总费用y=600x+800(20-x)+20×10=-200x+16200,
∵A型桌椅不少于12套,B型桌椅不少于6套,
∴,解得:12≤x≤14,
所以y与x之间的函数关系为y=-200x+16200(12≤x≤14,x为整数);
②由①知y=-200x+16200,且-200<0,
∴y随x的增大而减小,
∴当x=14时,总费用y最少,最少费用为-200×14+16200=13400元,
即购买A型桌椅14套、B型桌椅6套,总费用最少,最少总费用为13400元.
【点睛】
本题考查二元一次方程的应用、一次函数的应用、一元一次不等式组的应用,理解题意,正确列出方程或函数关系式是解答的关键.
2、 (1)36千米
(2)y=90x-24 (0.8≤x≤2)
(3)1.2小时
【解析】
【分析】
(1)由OA段可求得此时小龚驾车的速度,从而可求得36分钟离家的距离;
(2)用待定系数法.AB段过点A与B,把这两点的坐标代入所设函数解析式中即可求得函数解析式;
(3)由题意可得小龚离家的距离,根据(2)中求得的函数解析式的函数值,解方程即可求得x的值,从而求得小龚行驶的时间.
(1)
在OA段,小龚行驶的速度为:48÷0.8=60(千米/时),36分钟=0.6小时,则小龚出发36分钟时,离家的距离为60×0.6=36(千米);
(2)
由图象知: ,
设AB段的函数解析式为:
把A、B两点的坐标分别代入上式得:
解得:
∴AB段的函数解析式为(0.8≤x≤2)
(3)
由图象知,当小龚离目的地还有72千米时,他已行驶了156 72=84(千米)
所以在中,当y=84时,即,得
即小龚离目的地还有72千米,小龚行驶了1.2小时.
【点睛】
本题考查了一次函数(正比例函数)的图象与性质,待定系数法求函数解析式,已知函数值求自变量的值等知识,数形结合是本题的关键.
3、 (1)3.5小时,76;
(2)线段AD对应的函数表达式为.
(3)甲出发或或或小时,甲乙两车相距10km.
【解析】
【分析】
(1)根据乙车3小时到货站,在货站装货耗时半小时,得出小时,甲提前30分钟,可求甲车行驶的时间为:0.5+4.5=5小时,然后甲车速度=千米/时即可;
(2)利用待定系数法AD解析式为:,把AD两点坐标代入解析式得解方程即可;
(3)分两种情况,甲出发,乙未出发76t=10,乙出发后,设乙车的速度为xkm/h,利用行程列方程3x+(x-40)×1=380解方程求出x=105km/h,再用待定系数法,列方程,CD段乙车速度为105-40=65km/h,求出CD的解析式为,列方程,结合甲先行30分根据有理数加法求出甲所用时间即可.
(1)
解:∵3小时到货站,在货站装货耗时半小时,
∴小时,
甲车行驶的时间为:0.5+4.5=5小时,
甲车速度=千米/时,
故答案为:3.5小时,76;
(2)
点A表示的路程为:76×0.5=38,
设AD解析式为:,把AD两点坐标代入解析式得:
,
解得:,
线段AD对应的函数表达式为.
(3)
甲出发乙未出发,
∴76t=10,
∴t=,
乙出发后;
设乙车的速度为vkm/h,
3v+(v-40)×1=380
解得v=105km/h,
∴点B(3,315)
设OB解析式为,代入坐标得:,
∴OB解析式为
∴,
化简为:或,
解得或,
∵CD段乙车速度为105-40=65km/h,
设CD的解析式为代入点D坐标得,
,
解得:,
∴CD的解析式为,
∴,
解得:,
∵甲提前出发30分钟,
,,,
甲出发或或或小时,甲乙两车相距10km.
【点睛】
本题考查待定系数法求一次函数解析式,利用函数图像获取信息,绝对值方程,一元一次方程,二元一次方程组解法,分类讨论思想的应用使问题完整解决是解题关键.
4、 (1)w=-2x+810
(2)最省钱的购买方案是购进A型消毒液67瓶,购进B型消毒液23瓶,最低费用为676元
【解析】
【分析】
(1)A瓶个数为x,则B瓶个数为(90-x),根据题意列式计算即可;
(2)根据B型消毒液的数量不少于A型消毒液数量的,可以得到A型消毒液数量的取值范围,再根据一次函数的性质,即可求得最省钱的购买方案,计算出最少费用.
(1)
解:A瓶个数为x,则B瓶个数为(90-x),
依题意可得:w=7x+9(90-x)=-2x+810;
(2)
解:∵B型消毒液的数量不少于A型消毒液数量的,
∴,解得,
由(1)知w=﹣2x+810,
∴w随x的增大而减小,
∴当x=67时,w取得最小值,
此时w=﹣2×67+810=676,90﹣x=23,
答:最省钱的购买方案是购进A型消毒液67瓶,购进B型消毒液23瓶,最低费用为676元.
【点睛】
本题考查了一次函数的应用、二元一次方程组的应用、一元一次不等式的应用,解答本题的关键是列出相应的方程组和列出相应的函数关系式,利用一次函数的性质和不等式的性质解答.
5、 (1)
(2)
(3)13吨
【解析】
【分析】
(1)当0<x≤8时,根据水费=用水量×1.5,即可求出y与x的函数关系式;
(2)当x>8时,根据“每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费”,得出水费=8×1.5+(用水量-8)×2.2,即可求出y与x的函数关系式;
(3)当0<x≤8时,y≤12,由此可知这个月该户用水量超过8吨,将y=23代入(2)中所求的关系式,求出x的值即可.
(1)
根据题意可知:
当时,;
(2)
根据题意可知:
当时,;
(3)
当时,,
的最大值为(元,,
该户当月用水超过8吨.
令中,则,
解得:.
答:这个月该户用了13吨水.
【点睛】
本题考查了一次函数的应用,根据数量关系找出函数关系式是解题关键.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
