2011-2012学年第二学期阶段质量检测九年级数学(无答案)
文档属性
| 名称 | 2011-2012学年第二学期阶段质量检测九年级数学(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 42.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-16 00:00:00 | ||
图片预览

文档简介
2011-2012学年第二学期阶段质量检测
九年级数学
(时间:90分钟 分值120分)
第Ⅰ卷
一、选择题(每小题3分,共36分,每小题四个选项中只有一个是正确的,请将正确的选项序号填在右边的括号内)
1. 下列运算正确的是( )
A. B. C. D.
2.我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665 575 306人,将665575306用科学记数法表示(保留三个有效数字)约为( )
A. B. C. D.
3.点M(-sin60o,cos60o)关于轴对称的点的坐标是( )
A. B. C. D.
4.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,
且AB=CD,CE=1,DE=3,则⊙O的半径是( )
A. B. C. 2 D. 以上都不对
5.方程组的解是( )
A. B. C. D.
6.一元二次方程根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
7.由一些相同的小立方块搭成的几何体的三视图如图所示,
则搭成该几何体的小立方块有( )
A. 3块 B. 4块 C. 6块 D. 9块
8.已知多边形的每一个外角都是72o,则该多边形的内角和是( )
A. 1080o B. 720o C. 700o D. 540o
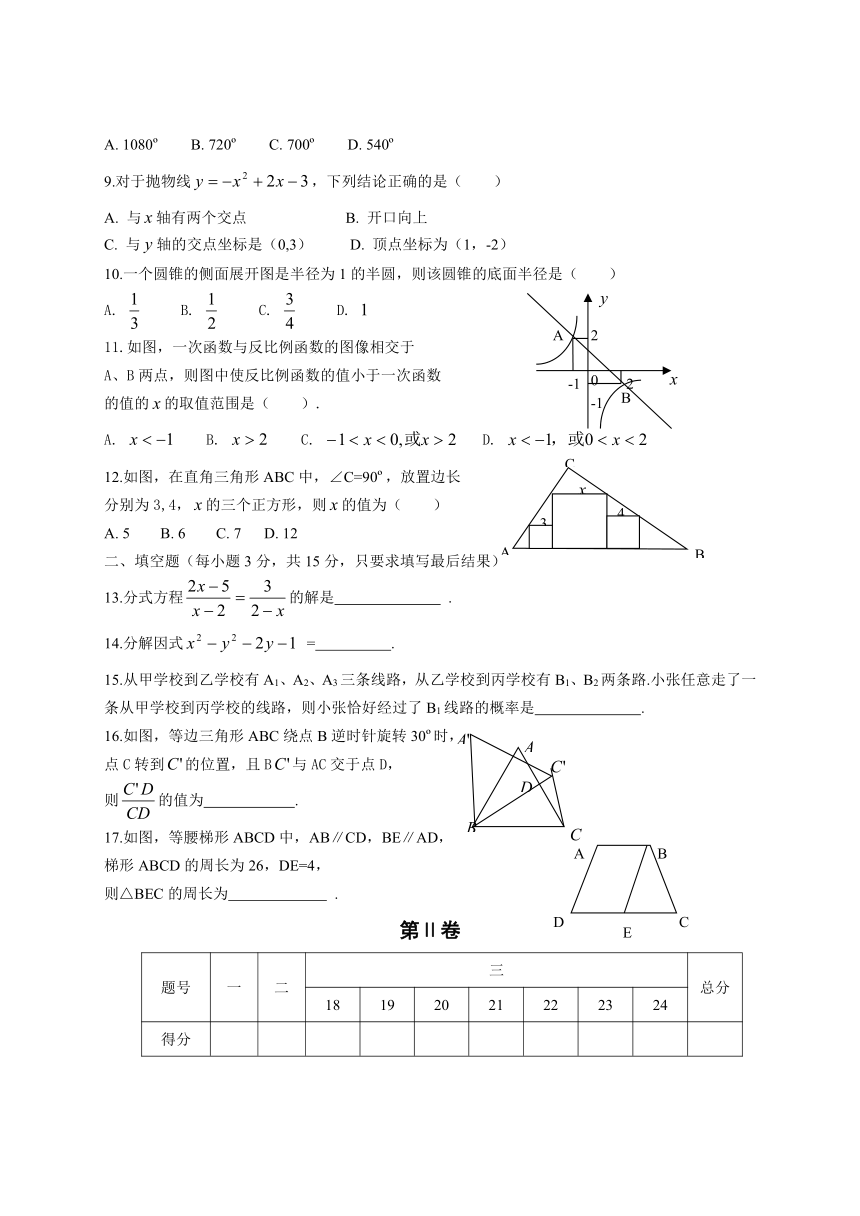
9.对于抛物线,下列结论正确的是( )
A. 与轴有两个交点 B. 开口向上
C. 与轴的交点坐标是(0,3) D. 顶点坐标为(1,-2)
10.一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是( )
A. B. C. D.
11.如图,一次函数与反比例函数的图像相交于
A、B两点,则图中使反比例函数的值小于一次函数
的值的的取值范围是( ).
A. B. C. D.
12.如图,在直角三角形ABC中,∠C=90o,放置边长
分别为3,4,的三个正方形,则的值为( )
A. 5 B. 6 C. 7 D. 12
二、填空题(每小题3分,共15分,只要求填写最后结果)
13.分式方程的解是 .
14.分解因式 = .
15.从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2两条路.小张任意走了一条从甲学校到丙学校的线路,则小张恰好经过了B1线路的概率是 .
16.如图,等边三角形ABC绕点B逆时针旋转30o时,
点C转到的位置,且B与AC交于点D,
则的值为 .
17.如图,等腰梯形ABCD中,AB∥CD,BE∥AD,
梯形ABCD的周长为26,DE=4,
则△BEC的周长为 .
第Ⅱ卷
题号
一
二
三
总分
18
19
20
21
22
23
24
得分
评卷人
一、选择题(每小题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每题3分,共24分)
13. ;14. ;
15. ;16. ;17. ;
三、解答题(解答应写出必要的计算过程、推演步骤或文字说明,共69分)
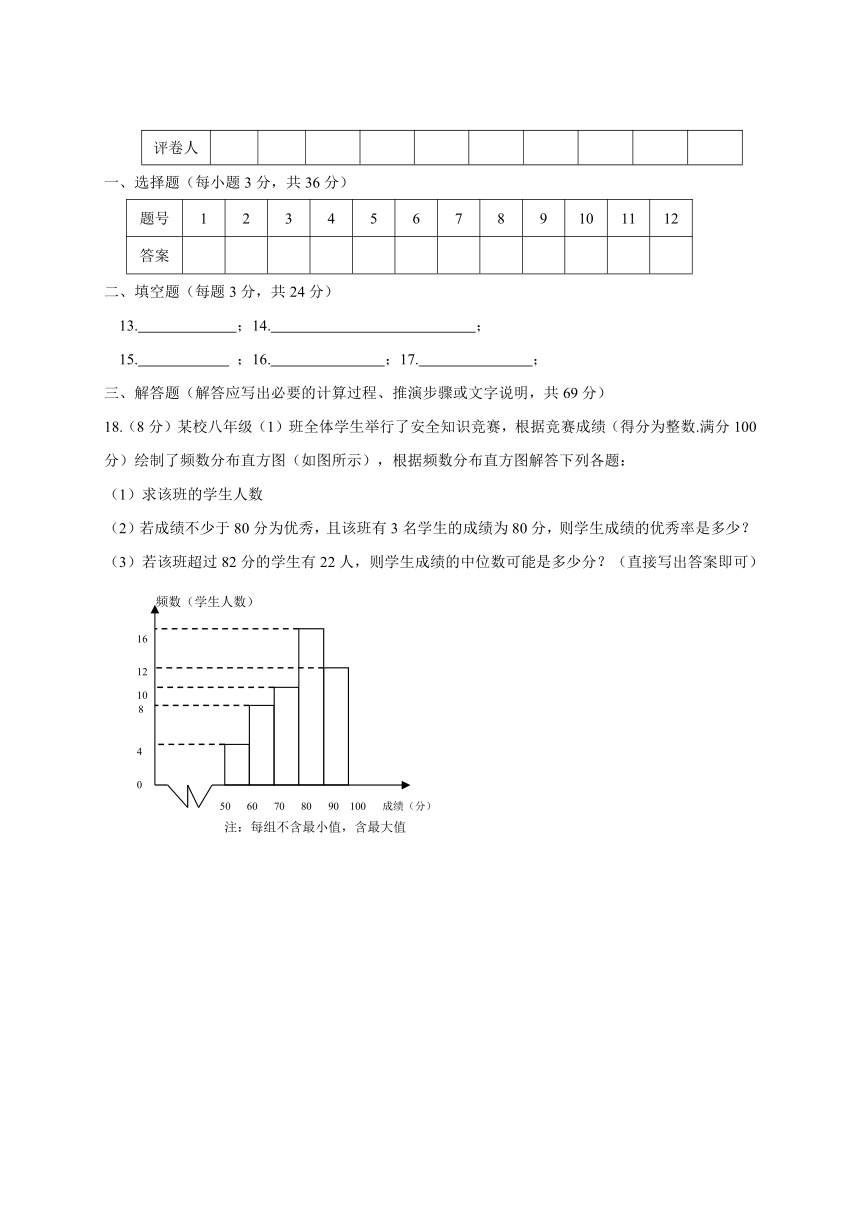
18.(8分)某校八年级(1)班全体学生举行了安全知识竞赛,根据竞赛成绩(得分为整数.满分100分)绘制了频数分布直方图(如图所示),根据频数分布直方图解答下列各题:
(1)求该班的学生人数
(2)若成绩不少于80分为优秀,且该班有3名学生的成绩为80分,则学生成绩的优秀率是多少?
(3)若该班超过82分的学生有22人,则学生成绩的中位数可能是多少分?(直接写出答案即可)
19.(9分)如图,点E、C在BF上,BE=FC,∠ABC=∠DEF=45o, ∠A=∠D=90o.
(1)求证AB=DE;
(2)若AC交DE于M,且AB=,ME=,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.
20.(9分)某工厂计划生产A、B两种产品共10件,其生产成本与利润如下表:
A种产品
B种产品
成本(万元/件)
3
5
利润(万元/件)
1
2
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种方案获利最大?并求最大利润.
21.(10分)如图,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边树立了一根水泥撑杆BD,用于撑起拉线.已知公路的宽AB为8米,电线杆AE的高是12米,水泥撑杆BD的高为6米,拉线CD与水平线AC的夹角为67.4o.求拉线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计)
(参考数据:sin67.4o≈ , cos67.4o≈ , tan67.4o≈)
22.(10分)某鸡场计划购买甲、乙两种小鸡苗2000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.
(1)若购买这批小鸡苗共用了4500元,求甲乙两种小鸡苗各购买了多少只?(2分)
(2)若购买这批小鸡苗的钱不超过4700元,问应选购甲种小鸡苗至少多少只?(3分)
(3)相关资料表明:甲、乙两种小鸡苗的成活率分别为94%和99%,若要使这批小鸡苗的成活率不低于96%且买小鸡的总费用最小,问应选购甲、乙两种小鸡苗各多少只?总费用最小是多少元?(5分)
23.(11分)如图,在△ABC中,∠C=90o,以AB上一点O为圆心,OA长为半径的圆与BC相切于D,分别交AC、AB于点E、F.
(1)若AC=6,AB=10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
24.(本题12分)如图,抛物线与轴交于A、B两点,与轴交于点
C(0,-3).
(1)求抛物线的对称轴及的值;
(2)抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积与此时点M的坐标.
九年级数学
(时间:90分钟 分值120分)
第Ⅰ卷
一、选择题(每小题3分,共36分,每小题四个选项中只有一个是正确的,请将正确的选项序号填在右边的括号内)
1. 下列运算正确的是( )
A. B. C. D.
2.我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665 575 306人,将665575306用科学记数法表示(保留三个有效数字)约为( )
A. B. C. D.
3.点M(-sin60o,cos60o)关于轴对称的点的坐标是( )
A. B. C. D.
4.如图,⊙O的两条弦AB、CD互相垂直,垂足为E,
且AB=CD,CE=1,DE=3,则⊙O的半径是( )
A. B. C. 2 D. 以上都不对
5.方程组的解是( )
A. B. C. D.
6.一元二次方程根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
7.由一些相同的小立方块搭成的几何体的三视图如图所示,
则搭成该几何体的小立方块有( )
A. 3块 B. 4块 C. 6块 D. 9块
8.已知多边形的每一个外角都是72o,则该多边形的内角和是( )
A. 1080o B. 720o C. 700o D. 540o
9.对于抛物线,下列结论正确的是( )
A. 与轴有两个交点 B. 开口向上
C. 与轴的交点坐标是(0,3) D. 顶点坐标为(1,-2)
10.一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是( )
A. B. C. D.
11.如图,一次函数与反比例函数的图像相交于
A、B两点,则图中使反比例函数的值小于一次函数
的值的的取值范围是( ).
A. B. C. D.
12.如图,在直角三角形ABC中,∠C=90o,放置边长
分别为3,4,的三个正方形,则的值为( )
A. 5 B. 6 C. 7 D. 12
二、填空题(每小题3分,共15分,只要求填写最后结果)
13.分式方程的解是 .
14.分解因式 = .
15.从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2两条路.小张任意走了一条从甲学校到丙学校的线路,则小张恰好经过了B1线路的概率是 .
16.如图,等边三角形ABC绕点B逆时针旋转30o时,
点C转到的位置,且B与AC交于点D,
则的值为 .
17.如图,等腰梯形ABCD中,AB∥CD,BE∥AD,
梯形ABCD的周长为26,DE=4,
则△BEC的周长为 .
第Ⅱ卷
题号
一
二
三
总分
18
19
20
21
22
23
24
得分
评卷人
一、选择题(每小题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(每题3分,共24分)
13. ;14. ;
15. ;16. ;17. ;
三、解答题(解答应写出必要的计算过程、推演步骤或文字说明,共69分)
18.(8分)某校八年级(1)班全体学生举行了安全知识竞赛,根据竞赛成绩(得分为整数.满分100分)绘制了频数分布直方图(如图所示),根据频数分布直方图解答下列各题:
(1)求该班的学生人数
(2)若成绩不少于80分为优秀,且该班有3名学生的成绩为80分,则学生成绩的优秀率是多少?
(3)若该班超过82分的学生有22人,则学生成绩的中位数可能是多少分?(直接写出答案即可)
19.(9分)如图,点E、C在BF上,BE=FC,∠ABC=∠DEF=45o, ∠A=∠D=90o.
(1)求证AB=DE;
(2)若AC交DE于M,且AB=,ME=,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.
20.(9分)某工厂计划生产A、B两种产品共10件,其生产成本与利润如下表:
A种产品
B种产品
成本(万元/件)
3
5
利润(万元/件)
1
2
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种方案获利最大?并求最大利润.
21.(10分)如图,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边树立了一根水泥撑杆BD,用于撑起拉线.已知公路的宽AB为8米,电线杆AE的高是12米,水泥撑杆BD的高为6米,拉线CD与水平线AC的夹角为67.4o.求拉线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计)
(参考数据:sin67.4o≈ , cos67.4o≈ , tan67.4o≈)
22.(10分)某鸡场计划购买甲、乙两种小鸡苗2000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.
(1)若购买这批小鸡苗共用了4500元,求甲乙两种小鸡苗各购买了多少只?(2分)
(2)若购买这批小鸡苗的钱不超过4700元,问应选购甲种小鸡苗至少多少只?(3分)
(3)相关资料表明:甲、乙两种小鸡苗的成活率分别为94%和99%,若要使这批小鸡苗的成活率不低于96%且买小鸡的总费用最小,问应选购甲、乙两种小鸡苗各多少只?总费用最小是多少元?(5分)
23.(11分)如图,在△ABC中,∠C=90o,以AB上一点O为圆心,OA长为半径的圆与BC相切于D,分别交AC、AB于点E、F.
(1)若AC=6,AB=10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
24.(本题12分)如图,抛物线与轴交于A、B两点,与轴交于点
C(0,-3).
(1)求抛物线的对称轴及的值;
(2)抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积与此时点M的坐标.
同课章节目录
