曲线与方程
图片预览







文档简介
课件24张PPT。2.1.1 曲线与方程画一画:1.第一、三象限夹角平分线
2.画出以(a,b)为圆心,r为半径的圆C如图,是直线表示y=x (x∈Z)的图象么?①满足y=x(x∈Z)的每一对有序实数对(x,y)都在直线上;②直线上每一个点(x,y)都满足方程y=x(x∈Z).思考:如图,是 圆表示
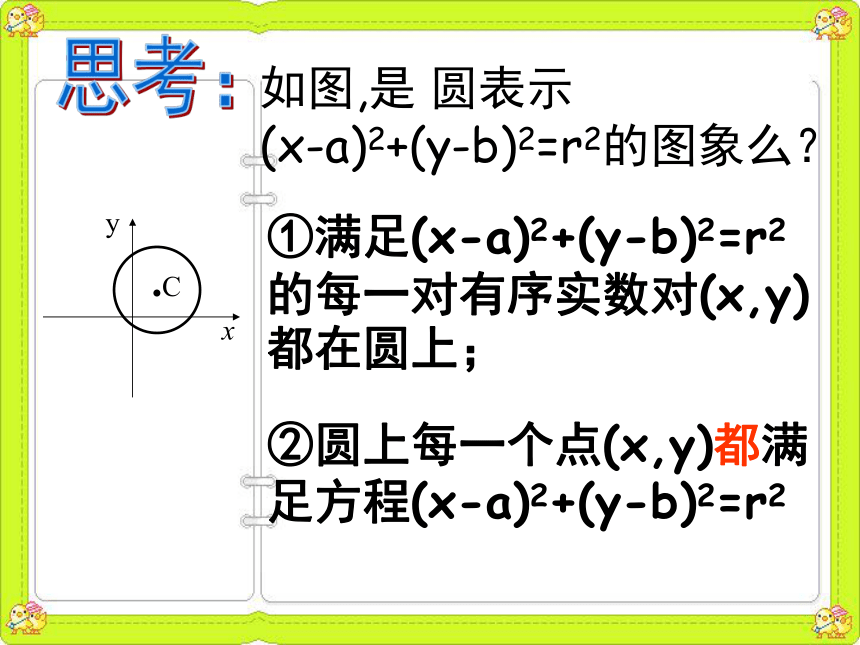
(x-a)2+(y-b)2=r2的图象么?①满足(x-a)2+(y-b)2=r2的每一对有序实数对(x,y)都在圆上;②圆上每一个点(x,y)都满足方程(x-a)2+(y-b)2=r2思考:教师总结:
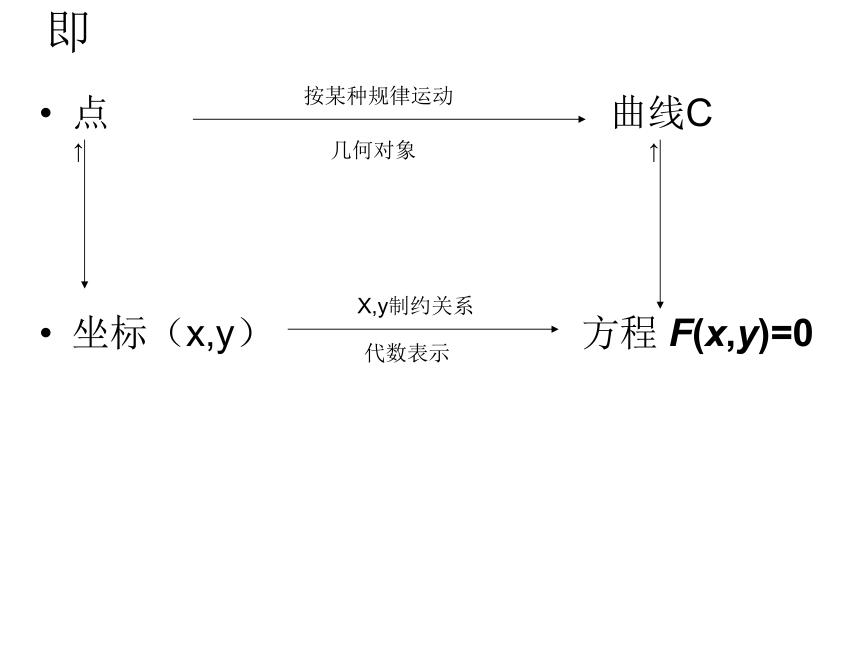
通过探索可知,在直角坐标系建立以后,平面内的点与数对(x,y)建立了一一对应关系。点的运动形成曲线C,与之对应的实数对的变化就形成了方程F(x,y)=0 。
即点 曲线C
坐标(x,y) 方程 F(x,y)=0 按某种规律运动几何对象 一般地,在直角坐标系中,如果某曲线C (看作点的集合或适合某种条件的点的轨迹)与二元方程f (x,y)=0的实数解建立了如下的关系:
(1)曲线上的点坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点.方程f(x,y)=0叫做这条曲线C的方程;
曲线C叫做这个方程f(x,y)=0的曲线.曲线的方程与方程的曲线
一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
(1)曲线上点的坐标都是这个方程的___;
(2)以这个方程的解为坐标的点都是曲线上的___.
那么这个方程叫做___________,这条曲线叫做_________
___.
自学导引解曲线的方程方程的曲点线【问题 】:证明与两条坐标轴的距离的积是常 数 的点的轨迹方程是 。证明:设 是轨迹上的任意一点,
则点 与两坐标轴的距离分别是| |、| |,
所以| |·| |= ,即 · = 。
故与两条坐标轴的距离的积是常数 ( >0)的点的轨迹方程是 。证明:(1)设 是轨迹上的任意一点,则点 与y轴、x轴的距离分别是︱ ︱、| |,所以| |·| |= 则, · = ,即( , )是方程 的解。
(2)设( , )是方程的解,则 · = ,即 ︱ ︱·| |= ,而︱ ︱、︱ |是点( , )到y轴、x轴的距离,因此该点到这两条坐标轴的距离的积是常数 ,它是轨迹上的点。
由(1)(2)可知与两条坐标轴的距离的积是常数 ( >0)的点的轨迹方程是 。 第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:
证明已知曲线的方程的方法和步骤 第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.题型一 曲线与方程的概念 若命题“曲线C上的点的坐标都是方程f(x,y)=0的
解”是正确的,则下列命题为真命题的是 ( ).
A.不是曲线C上的点的坐标,一定不满足方程f(x,y)=0
B.坐标满足方程f(x,y)=0的点均在曲线C上
C.曲线C是方程f(x,y)=0的曲线
D.不是方程f(x,y)=0的解,一定不是曲线C上的点
[思路探索] 从定义入手,考查定义中的两个条件.
【例1】解析 ∵题设命题只说明“曲线C上的点的坐标都是方程f(x,y)=0的解”,并未指出“以方程f(x,y)=0的解为坐标的点都是曲线C上的点”,
∴A、B、C都是假命题,如曲线C:平面直角坐标系一、三象限角平分线上的点,与方程f(x,y)=x2-y2=0,满足题设条件,但却不满足选项A、B、C的结论,根据逆否命题是原命题的等价命题知,D是正确的.
答案 D
方程x2+y2=1(xy<0)的曲线形状是 ( ).
【变式2】解析 方程x2+y2=1表示以原点为圆心,半径为1的单位圆,而约束条件xy<0则表明单位圆上点的横、纵坐标异号,即单位圆位于第二或第四象限的部分.
答案 C
活页规范训练1.已知坐标满足方程F(x,y)=0的点都在曲线C上,那么 ( ).
A.曲线C上的点的坐标都适合方程F(x,y)=0
B.凡坐标不适合F(x,y)=0的点都不在C上
C.不在C上的点的坐标必不适合F(x,y)=0
D.不在C上的点的坐标有些适合F(x,y)=0,有些不适合F(x,y)=0
答案 C2.下列选项中方程表示图中曲线的是 ( ).
解析 对于A,x2+y2=1表示一个整圆;对于B,x2-y2=(x+y)(x-y)=0,表示两条相
交直线;对于D,由lg x+lg y=0知x>0,y>0.
答案 C3.方程x2+xy=x表示的曲线是 ( ).
A.一个点 B.一条直线
C.两条直线 D.一个点和一条直线
解析 由x2+xy=x,得x(x+y-1)=0,即x=0或x+y-1=0.由此知方程x2+xy=x表
示两条直线.故选C.
答案 C5.方程y= 所表示的曲线是______.
解析 y= =|x-1|.
答案 以(1,0)为端点的两条射线7.方程(x2-4)2+(y2-4)2=0表示的图形是 ( ).
A.两个点 B.四个点
C.两条直线 D.四条直线
解析 由已知 ∴
即 或 或 或 .
答案 B8.下面四组方程表示同一条曲线的一组是 ( ).
A.y2=x与y=
B.y=lg x2与y=2lg x
C. =1与lg (y+1)=lg (x-2)
D.x2+y2=1与|y|=
解析 主要考虑x与y的范围.
答案 D9.已知方程①x-y=0;② - =0;③x2-y2=0;④ =1,其中能表示直角坐标系的第一、三象限的角平分线C的方程的序号是________.
解析 ①是正确的;
②不正确,如点(-1,-1)在第三象限的角平分线上,但其坐标不满足方程 - =0;
③不正确.如点(-1,1)满足方程x2-y2=0,但它不在曲线C上;
④不正确.如点(0,0)在曲线C上,但其坐标不满足方程 =1.
答案 ①12.(创新拓展)已知曲线C的方程为x= ,说明曲线C是什么样的曲线,并求该曲线与y轴围成的图形的面积.
解 由x= ,得x2+y2=4.
又x≥0,∴方程x= 表示的曲线是以原点为圆心,2为半径的右半圆,
从而该曲线C与y轴围成的图形是半圆,
其面积S= π·4=2π.
所以所求图形的面积为2π.
2.画出以(a,b)为圆心,r为半径的圆C如图,是直线表示y=x (x∈Z)的图象么?①满足y=x(x∈Z)的每一对有序实数对(x,y)都在直线上;②直线上每一个点(x,y)都满足方程y=x(x∈Z).思考:如图,是 圆表示
(x-a)2+(y-b)2=r2的图象么?①满足(x-a)2+(y-b)2=r2的每一对有序实数对(x,y)都在圆上;②圆上每一个点(x,y)都满足方程(x-a)2+(y-b)2=r2思考:教师总结:
通过探索可知,在直角坐标系建立以后,平面内的点与数对(x,y)建立了一一对应关系。点的运动形成曲线C,与之对应的实数对的变化就形成了方程F(x,y)=0 。
即点 曲线C
坐标(x,y) 方程 F(x,y)=0 按某种规律运动几何对象 一般地,在直角坐标系中,如果某曲线C (看作点的集合或适合某种条件的点的轨迹)与二元方程f (x,y)=0的实数解建立了如下的关系:
(1)曲线上的点坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点.方程f(x,y)=0叫做这条曲线C的方程;
曲线C叫做这个方程f(x,y)=0的曲线.曲线的方程与方程的曲线
一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
(1)曲线上点的坐标都是这个方程的___;
(2)以这个方程的解为坐标的点都是曲线上的___.
那么这个方程叫做___________,这条曲线叫做_________
___.
自学导引解曲线的方程方程的曲点线【问题 】:证明与两条坐标轴的距离的积是常 数 的点的轨迹方程是 。证明:设 是轨迹上的任意一点,
则点 与两坐标轴的距离分别是| |、| |,
所以| |·| |= ,即 · = 。
故与两条坐标轴的距离的积是常数 ( >0)的点的轨迹方程是 。证明:(1)设 是轨迹上的任意一点,则点 与y轴、x轴的距离分别是︱ ︱、| |,所以| |·| |= 则, · = ,即( , )是方程 的解。
(2)设( , )是方程的解,则 · = ,即 ︱ ︱·| |= ,而︱ ︱、︱ |是点( , )到y轴、x轴的距离,因此该点到这两条坐标轴的距离的积是常数 ,它是轨迹上的点。
由(1)(2)可知与两条坐标轴的距离的积是常数 ( >0)的点的轨迹方程是 。 第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:
证明已知曲线的方程的方法和步骤 第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.题型一 曲线与方程的概念 若命题“曲线C上的点的坐标都是方程f(x,y)=0的
解”是正确的,则下列命题为真命题的是 ( ).
A.不是曲线C上的点的坐标,一定不满足方程f(x,y)=0
B.坐标满足方程f(x,y)=0的点均在曲线C上
C.曲线C是方程f(x,y)=0的曲线
D.不是方程f(x,y)=0的解,一定不是曲线C上的点
[思路探索] 从定义入手,考查定义中的两个条件.
【例1】解析 ∵题设命题只说明“曲线C上的点的坐标都是方程f(x,y)=0的解”,并未指出“以方程f(x,y)=0的解为坐标的点都是曲线C上的点”,
∴A、B、C都是假命题,如曲线C:平面直角坐标系一、三象限角平分线上的点,与方程f(x,y)=x2-y2=0,满足题设条件,但却不满足选项A、B、C的结论,根据逆否命题是原命题的等价命题知,D是正确的.
答案 D
方程x2+y2=1(xy<0)的曲线形状是 ( ).
【变式2】解析 方程x2+y2=1表示以原点为圆心,半径为1的单位圆,而约束条件xy<0则表明单位圆上点的横、纵坐标异号,即单位圆位于第二或第四象限的部分.
答案 C
活页规范训练1.已知坐标满足方程F(x,y)=0的点都在曲线C上,那么 ( ).
A.曲线C上的点的坐标都适合方程F(x,y)=0
B.凡坐标不适合F(x,y)=0的点都不在C上
C.不在C上的点的坐标必不适合F(x,y)=0
D.不在C上的点的坐标有些适合F(x,y)=0,有些不适合F(x,y)=0
答案 C2.下列选项中方程表示图中曲线的是 ( ).
解析 对于A,x2+y2=1表示一个整圆;对于B,x2-y2=(x+y)(x-y)=0,表示两条相
交直线;对于D,由lg x+lg y=0知x>0,y>0.
答案 C3.方程x2+xy=x表示的曲线是 ( ).
A.一个点 B.一条直线
C.两条直线 D.一个点和一条直线
解析 由x2+xy=x,得x(x+y-1)=0,即x=0或x+y-1=0.由此知方程x2+xy=x表
示两条直线.故选C.
答案 C5.方程y= 所表示的曲线是______.
解析 y= =|x-1|.
答案 以(1,0)为端点的两条射线7.方程(x2-4)2+(y2-4)2=0表示的图形是 ( ).
A.两个点 B.四个点
C.两条直线 D.四条直线
解析 由已知 ∴
即 或 或 或 .
答案 B8.下面四组方程表示同一条曲线的一组是 ( ).
A.y2=x与y=
B.y=lg x2与y=2lg x
C. =1与lg (y+1)=lg (x-2)
D.x2+y2=1与|y|=
解析 主要考虑x与y的范围.
答案 D9.已知方程①x-y=0;② - =0;③x2-y2=0;④ =1,其中能表示直角坐标系的第一、三象限的角平分线C的方程的序号是________.
解析 ①是正确的;
②不正确,如点(-1,-1)在第三象限的角平分线上,但其坐标不满足方程 - =0;
③不正确.如点(-1,1)满足方程x2-y2=0,但它不在曲线C上;
④不正确.如点(0,0)在曲线C上,但其坐标不满足方程 =1.
答案 ①12.(创新拓展)已知曲线C的方程为x= ,说明曲线C是什么样的曲线,并求该曲线与y轴围成的图形的面积.
解 由x= ,得x2+y2=4.
又x≥0,∴方程x= 表示的曲线是以原点为圆心,2为半径的右半圆,
从而该曲线C与y轴围成的图形是半圆,
其面积S= π·4=2π.
所以所求图形的面积为2π.
