2021—2022学年苏科版数学八年级下册9.1图形的旋转课件(共27张PPT)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级下册9.1图形的旋转课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1005.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 16:33:28 | ||
图片预览







文档简介
(共27张PPT)
2022
9.1 图形的旋转
八年级下册
学习目标
1.认识旋转,寻找现实生活中的旋转现象。
2.理解图形旋转的基本性质。
重点
分析研究旋转现象,探索旋转的性质。
难点
1.图形旋转的变换关系。
2.理解平移、旋转、轴对称的区别与联系。
情景创设
1
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
议题引领
2
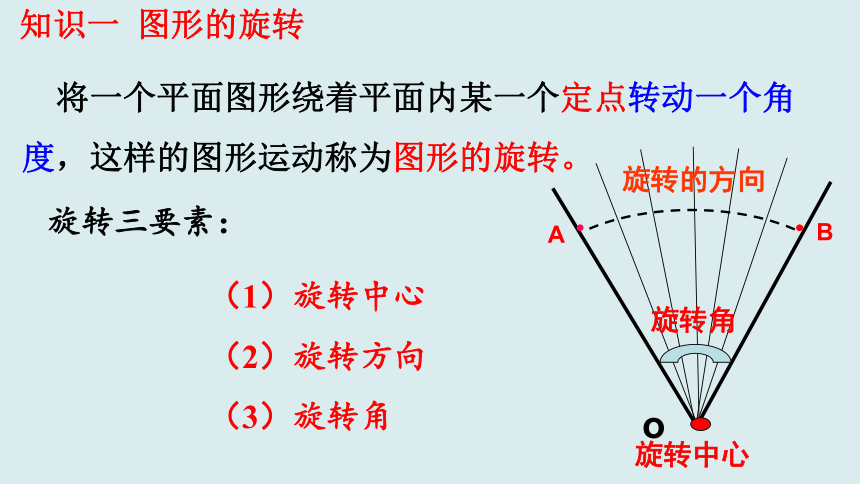
将一个平面图形绕着平面内某一个定点转动一个角度,这样的图形运动称为图形的旋转。
知识一 图形的旋转
旋转角
旋转中心
A
o
B
旋转的方向
.
.
旋转三要素:
(1)旋转中心
(2)旋转方向
(3)旋转角
下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.属于旋转的有( )
A. 2 个 B. 3 个
C. 4 个 D. 5 个
C
例1
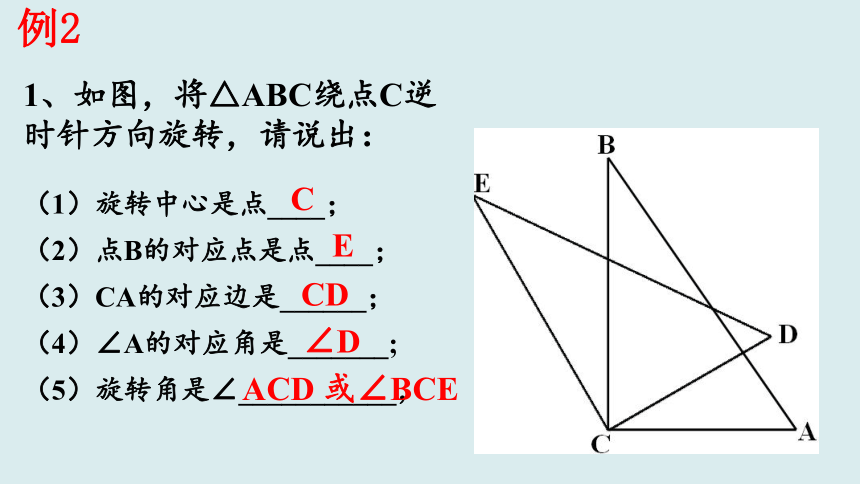
1、如图,将△ABC绕点C逆时针方向旋转,请说出:
(1)旋转中心是点____;
(2)点B的对应点是点____;
(3)CA的对应边是______;
(4)∠A的对应角是_______;
(5)旋转角是∠___________,
C
E
CD
∠D
ACD 或∠BCE
例2
在图形旋转的过程中
哪些发生了改变?
哪些没有发生改变?
A
B
B′
A′
C
.
旋转前后图形位置改变,
形状大小都没有改变
想一想
·
·
·
O
C
B
A
A’
C’
B’
问题①:旋转前后,△A’B’C’与△ABC有怎样的关系?
问题③:∠AOA’、∠BOB’、∠COC’度数有怎样的关系?
问题②:比较OA与OA’、OB与OB’ 、OC与OC’的长度,有怎样的关系?
性质①:旋转前、后的两个图形全等 即:△A’B’C’≌△ABC
性质②:对应点到旋转中心的距离相等。即:OA=OA’、OB=OB’ 、OC=OC’
性质③:每一对对应点与旋转中心的连线所成的角彼此相等
即:∠AOA’=∠BOB’=∠COC’
知识二 旋转的性质
如图,将△AOB绕点O逆时针旋转后与△COD重合,
B
O
A
C
D
①指出这一旋转的旋转中心和旋转角;
②说出图中相等的线段
③说出图中相等的角.
解:①旋转中心是点O;
旋转角是∠AOC或∠BOD;
②相等的线段:OB=OD,OA=OC,AB=CD;
③相等的角:
∠BOD=∠AOC,∠A=∠C,∠B=∠D,∠BOA=∠DOC
例3
如图,将△ ABC 绕点C 按顺时针方向旋转至△A′B′C,使点A′ 落在BC 的延长线上,已知∠ A=30°,
∠ B=40°,求旋转角的度数.
例4
解:∵∠ A=30°,∠ B=40°,
∴∠ ACA′= ∠ A+ ∠ B=30° +40° =70° .
∵△ ABC 绕点C 按顺时针方向旋转至△ A′B′C,
∴旋转角的度数为70° .
合作学习
3
已知点A和点O,请画出点A绕点O按顺时针方向旋转90°后的图形.
A
O
所以,点A′就是所要求作的点
步骤:
(1)连线
(2)画角
(3)截取
点绕点旋转
A′
90°
(5)连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。
A'
B'
B
A
O
D
C
已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。
(1)连接OA
(2)作∠AOC=100°,在OC上截取OA'=OA
(4)作∠BOD=100°,在OD上截取OB'=OB
(3)连接OB
线段绕点旋转
画出将△ABC绕点C按逆时针方向旋转1200后的对应三角形。
A
B
C
B'
A'
1200
图形绕点旋转
注:作旋转后的图形可以转化为作关键点旋转后的对应点
(1)定:确定旋转中心、旋转方向、旋转角;
(2)找:找出图形上的关键点;
(3)作:连接图形上的关键点与旋转中心,然后按旋转方向分别将它们旋转一定的角度,作出关键点的对应点;
(4)连:按原图的顺序连接这些对应点,即得旋转后的图形;
(5)写:写出结论,说明作出的图形即为所求作的图形.
知识三 旋转图形的做法
如图,△ ABC 绕点O 旋转,使点A 旋转到点D 处,画出顺时针旋转后的三角形,并写出简要作法.
随堂练习
B
O
C
A
D
B
O
C
A
D
E
F
作法:
(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
·
M
N
随堂练习
确定旋转中心的方法:
在图形的旋转过程中,判断旋转中心的位置,要看旋转中心是在图形上还是不在图形上.
若在图形上,哪一点在旋转的过程中位置没有改变,哪一点就是旋转中心.
若不在图形上,对应点连线的垂直平分线的交点就是旋转中心.
拓展延伸
成果展示
4
旋转
定义
三要素:旋转中心,旋转方向,旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
作旋转图形
定、找、作、连、写
检测反馈
5
1.下列运动属于旋转的是 ( )
A.足球在草地上滚动
B.火箭升空的运动
C.汽车在急刹车时向前滑行
D.钟表的钟摆摆动的过程
D
2.如图是香港特别行政区区徽中的紫荆花图案,该图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A.45° B.60° C.72° D.108°
C
课堂反馈
3.如图,△AOC逆时针旋转得到△BOD,其中∠AOC=120°,点A,O,D在同一直线上.
(1)旋转中心是哪一点
(2)旋转角为多少度
(3)指出图中的对应线段、对应角及对应点.
60°
点O
课堂反馈
4.如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格
点.△ABC的三个顶点A,B,C
都在格点上,将△ABC绕点A
顺时针旋转90°得到△AB'C',
在正方形网格中,画出△AB'C'.
课堂反馈
2022
9.1 图形的旋转
八年级下册
学习目标
1.认识旋转,寻找现实生活中的旋转现象。
2.理解图形旋转的基本性质。
重点
分析研究旋转现象,探索旋转的性质。
难点
1.图形旋转的变换关系。
2.理解平移、旋转、轴对称的区别与联系。
情景创设
1
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
议题引领
2
将一个平面图形绕着平面内某一个定点转动一个角度,这样的图形运动称为图形的旋转。
知识一 图形的旋转
旋转角
旋转中心
A
o
B
旋转的方向
.
.
旋转三要素:
(1)旋转中心
(2)旋转方向
(3)旋转角
下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.属于旋转的有( )
A. 2 个 B. 3 个
C. 4 个 D. 5 个
C
例1
1、如图,将△ABC绕点C逆时针方向旋转,请说出:
(1)旋转中心是点____;
(2)点B的对应点是点____;
(3)CA的对应边是______;
(4)∠A的对应角是_______;
(5)旋转角是∠___________,
C
E
CD
∠D
ACD 或∠BCE
例2
在图形旋转的过程中
哪些发生了改变?
哪些没有发生改变?
A
B
B′
A′
C
.
旋转前后图形位置改变,
形状大小都没有改变
想一想
·
·
·
O
C
B
A
A’
C’
B’
问题①:旋转前后,△A’B’C’与△ABC有怎样的关系?
问题③:∠AOA’、∠BOB’、∠COC’度数有怎样的关系?
问题②:比较OA与OA’、OB与OB’ 、OC与OC’的长度,有怎样的关系?
性质①:旋转前、后的两个图形全等 即:△A’B’C’≌△ABC
性质②:对应点到旋转中心的距离相等。即:OA=OA’、OB=OB’ 、OC=OC’
性质③:每一对对应点与旋转中心的连线所成的角彼此相等
即:∠AOA’=∠BOB’=∠COC’
知识二 旋转的性质
如图,将△AOB绕点O逆时针旋转后与△COD重合,
B
O
A
C
D
①指出这一旋转的旋转中心和旋转角;
②说出图中相等的线段
③说出图中相等的角.
解:①旋转中心是点O;
旋转角是∠AOC或∠BOD;
②相等的线段:OB=OD,OA=OC,AB=CD;
③相等的角:
∠BOD=∠AOC,∠A=∠C,∠B=∠D,∠BOA=∠DOC
例3
如图,将△ ABC 绕点C 按顺时针方向旋转至△A′B′C,使点A′ 落在BC 的延长线上,已知∠ A=30°,
∠ B=40°,求旋转角的度数.
例4
解:∵∠ A=30°,∠ B=40°,
∴∠ ACA′= ∠ A+ ∠ B=30° +40° =70° .
∵△ ABC 绕点C 按顺时针方向旋转至△ A′B′C,
∴旋转角的度数为70° .
合作学习
3
已知点A和点O,请画出点A绕点O按顺时针方向旋转90°后的图形.
A
O
所以,点A′就是所要求作的点
步骤:
(1)连线
(2)画角
(3)截取
点绕点旋转
A′
90°
(5)连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。
A'
B'
B
A
O
D
C
已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。
(1)连接OA
(2)作∠AOC=100°,在OC上截取OA'=OA
(4)作∠BOD=100°,在OD上截取OB'=OB
(3)连接OB
线段绕点旋转
画出将△ABC绕点C按逆时针方向旋转1200后的对应三角形。
A
B
C
B'
A'
1200
图形绕点旋转
注:作旋转后的图形可以转化为作关键点旋转后的对应点
(1)定:确定旋转中心、旋转方向、旋转角;
(2)找:找出图形上的关键点;
(3)作:连接图形上的关键点与旋转中心,然后按旋转方向分别将它们旋转一定的角度,作出关键点的对应点;
(4)连:按原图的顺序连接这些对应点,即得旋转后的图形;
(5)写:写出结论,说明作出的图形即为所求作的图形.
知识三 旋转图形的做法
如图,△ ABC 绕点O 旋转,使点A 旋转到点D 处,画出顺时针旋转后的三角形,并写出简要作法.
随堂练习
B
O
C
A
D
B
O
C
A
D
E
F
作法:
(1)连接OA,OB,OC,OD;
(2)分别以OB,OC为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
·
M
N
随堂练习
确定旋转中心的方法:
在图形的旋转过程中,判断旋转中心的位置,要看旋转中心是在图形上还是不在图形上.
若在图形上,哪一点在旋转的过程中位置没有改变,哪一点就是旋转中心.
若不在图形上,对应点连线的垂直平分线的交点就是旋转中心.
拓展延伸
成果展示
4
旋转
定义
三要素:旋转中心,旋转方向,旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
作旋转图形
定、找、作、连、写
检测反馈
5
1.下列运动属于旋转的是 ( )
A.足球在草地上滚动
B.火箭升空的运动
C.汽车在急刹车时向前滑行
D.钟表的钟摆摆动的过程
D
2.如图是香港特别行政区区徽中的紫荆花图案,该图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )
A.45° B.60° C.72° D.108°
C
课堂反馈
3.如图,△AOC逆时针旋转得到△BOD,其中∠AOC=120°,点A,O,D在同一直线上.
(1)旋转中心是哪一点
(2)旋转角为多少度
(3)指出图中的对应线段、对应角及对应点.
60°
点O
课堂反馈
4.如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格
点.△ABC的三个顶点A,B,C
都在格点上,将△ABC绕点A
顺时针旋转90°得到△AB'C',
在正方形网格中,画出△AB'C'.
课堂反馈
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
