2021-2022学年苏科版八年级数学下册第8章认识概率 复习课课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册第8章认识概率 复习课课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 276.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 16:48:05 | ||
图片预览






文档简介
(共16张PPT)
2022
第八章 认识概率复习课
八年级下册
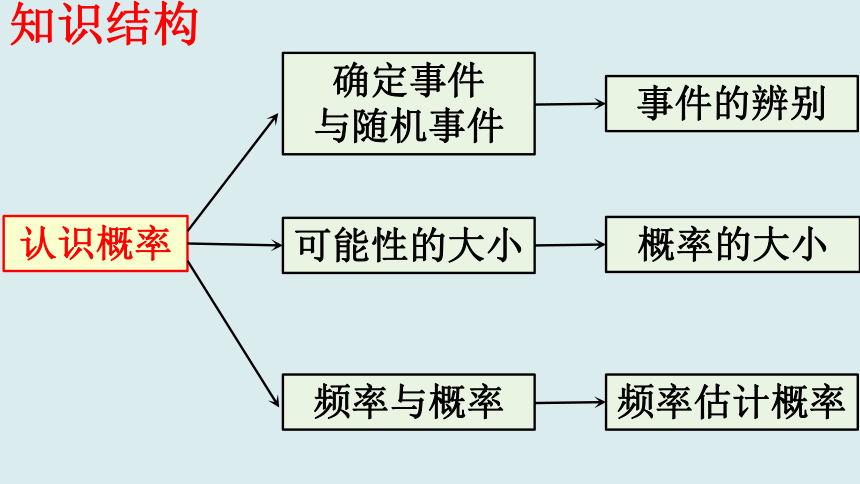
知识结构
认识概率
确定事件
与随机事件
可能性的大小
频率与概率
事件的辨别
概率的大小
频率估计概率
知识回顾
确定事件与随机事件
(1)事先能肯定一定会发生的事情叫必然事件
(2)事先能肯定一定不会发生的事情叫不可能事件
注意:
(3)事先无法确定会不会发生的事情叫随机事件
必然事件和不可能事件都是确定事件
典例分析
确定事件与随机事件
例1 如图,一只不透明的袋子中装有3个黄球和2个红球,这些球除颜色外都相同.判断下列事件是必然事件、不可能事件,还是随机事件?
随机事件
不可能事件
随机事件
必然事件
(1) 从袋子中任意摸出一个球,该球是白球.
(2) 从袋子中任意摸出一个球,该球是黄球.
(3) 从袋子中任意摸出一个球,该球是红球.
(4) 从袋子中任意摸出一个球,该球要么是红球,要么是黄球.
巩固小练
确定事件与随机事件
1.判断下列哪些事件是必然事件、不可能事件、随机事件?
(1)如果a,b都是有理数,那么a+b=b+a .
(2)从分别标有1-10的10张标签中任取 1张,得到8号签.
(3)没有水分,种子发芽.
(4)某人射击一次,中靶.
(5)“守株待兔”.
(6)“水中捞月”.
必然事件
随机事件
不可能事件
随机事件
随机事件
不可能事件
知识回顾
可能性的大小
(1)随机事件发生的可能性有大有小.
事件发生的可能性大小的数值,称为这个事件发生的概率
(2)若用A表示一个事件,则我们用P(A)表示事件A发生的概率.
必然事件发生的概率是 1,记作 P(A) = 1;
不可能事件发生的概率为 0,记作 P(A) = 0;
随机事件发生的概率是0和1之间的一个数,即0< P(A) <1.
可能性的大小
典例分析
例2 如图,一只不透明的袋子中装有3个黄球、2个红球和1个蓝球,这些球除颜色外都相同.将球摇匀,从中任意摸出1个球.
(3)怎样改变袋子中黄球、红球、蓝球的个数,
使摸到这三种颜色的球的可能性相等?
(1)能事先确定摸到的这个球的颜色吗?
(2)你认为摸到哪种颜色的球的可能性最大?
不能确定.
摸到黄球的可能性最大.
只要使得袋子中蓝球、黄球、红球的个数相等.
可能性的大小
巩固练习
1.如图,转盘中8个扇形的面积都相等,任意转
动转盘1次,当转盘停止转动时,估计下列事件
发生的可能性的大小,并将这些事件的序号
按发生的可能性从小到大的顺序排列:
(1)指针落在标有5的区域内;
(2)指针落在标有10的区域内;
(3)指针落在标有偶数或奇数的区域内;
(4)指针落在标有奇数的区域内.
按发生的可能性从小到大的顺序排列为:(2)<(1)<(4)<(3)
1
2
3
4
5
6
7
8
不可能事件,它的概率为0
必然事件,它的概率为1
发生的可能性较大
发生的可能性较小
知识回顾
频率与概率
(1)通常,在多次重复实验中,一个随机事件发生的频
率会在某一个常数附近摆动,且趋于稳定,这个性质称
为 频率的稳定性.
(2)用频率估计一个随机事件发生的概率,通常要经历“试验并收集、整理、描述数据——计算频率——估计概
率”的过程.(注意:这里的“试验”,必须在相同条件
下进行,且试验的次数要足够多.)
例3 一只不透明的袋子中装有若干个白球和其他颜色的球,这些球除颜色外都相同.每次从袋子中摸出一个球,然后放回摇匀再摸,在摸球实验中得到下列表中的部分数据:
摸球次数 40 80 400 600 800 1000 1200 1500
摸出白球的频数 14 26 128 198 267 399 500
摸出白球的频率 0.325 0.320 0.330 0.334 0.332 0.333 0.333
(1)请将表补充完整;
332
0.350
14÷40=0.350
频率与概率
典例分析
1 000×0.332=332
频率与概率
典例分析
(2)画出“摸出白球”的频率折线统计图,得摸出白球的概率估计值
是________;(精确到到0.01)
(3)若袋中共有100个球,则袋中可能有____个白球.
0.33
100×0.33=33
33
巩固练习
频率与概率
1.小杨、小刚用摸球游戏决定谁去看电影,袋中有1个红球和1个白球(除颜色不同外其余相同),得到红球为“看”,得到白球为“不看”,小杨先摸,另一个球留给小刚,这个游戏对双方是 . (填“公平”或“不公平”)
2.在一个有10万人的小镇上,随机调查了2000人,其中有400人看中央电视台的早间新闻,在该镇随便问一人,他看中央电视台早间新闻的概率大约是 .
公平
0.2
巩固练习
频率与概率
3.某次活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表格是此次活动中的一组统计数据:
转动转盘的次数n 100 200 300 400 500 1000
落在“书画”区域的次数m 60 122 180 242 a 604
落在“书画”区域的频率 0.60 0.61 0.60 b 0.59 0.604
巩固练习
频率与概率
(1)完成上述表格:a = ;b = ;
(2)请估计当n很大时,频率将会接近 ,假如你去转动该转
盘一次,获得“书画”的概率大约是 .(结果全部精确到0.1)
295
0.605
0.6
0.6
巩固练习
频率与概率
4.某批乒乓球的质量检验结果如下:
抽取的乒乓球数n 50 100 200 500 1 000 1 500 2 000
优等品的频数m 48 95 188 471 946 1426 1898
优等品的频率m/n(精确到0.001)
0.960
0.950 0.940 0.942 0.946 0.951 0.949
(1)请将上表补充完整;
巩固练习
频率与概率
(2)画出优等品频率的折线统计图;
(3)从这批乒乓球中,任意抽取的一只乒乓球是优等品的概率的估计值是_________;(精确到0.01)
0.95
2022
第八章 认识概率复习课
八年级下册
知识结构
认识概率
确定事件
与随机事件
可能性的大小
频率与概率
事件的辨别
概率的大小
频率估计概率
知识回顾
确定事件与随机事件
(1)事先能肯定一定会发生的事情叫必然事件
(2)事先能肯定一定不会发生的事情叫不可能事件
注意:
(3)事先无法确定会不会发生的事情叫随机事件
必然事件和不可能事件都是确定事件
典例分析
确定事件与随机事件
例1 如图,一只不透明的袋子中装有3个黄球和2个红球,这些球除颜色外都相同.判断下列事件是必然事件、不可能事件,还是随机事件?
随机事件
不可能事件
随机事件
必然事件
(1) 从袋子中任意摸出一个球,该球是白球.
(2) 从袋子中任意摸出一个球,该球是黄球.
(3) 从袋子中任意摸出一个球,该球是红球.
(4) 从袋子中任意摸出一个球,该球要么是红球,要么是黄球.
巩固小练
确定事件与随机事件
1.判断下列哪些事件是必然事件、不可能事件、随机事件?
(1)如果a,b都是有理数,那么a+b=b+a .
(2)从分别标有1-10的10张标签中任取 1张,得到8号签.
(3)没有水分,种子发芽.
(4)某人射击一次,中靶.
(5)“守株待兔”.
(6)“水中捞月”.
必然事件
随机事件
不可能事件
随机事件
随机事件
不可能事件
知识回顾
可能性的大小
(1)随机事件发生的可能性有大有小.
事件发生的可能性大小的数值,称为这个事件发生的概率
(2)若用A表示一个事件,则我们用P(A)表示事件A发生的概率.
必然事件发生的概率是 1,记作 P(A) = 1;
不可能事件发生的概率为 0,记作 P(A) = 0;
随机事件发生的概率是0和1之间的一个数,即0< P(A) <1.
可能性的大小
典例分析
例2 如图,一只不透明的袋子中装有3个黄球、2个红球和1个蓝球,这些球除颜色外都相同.将球摇匀,从中任意摸出1个球.
(3)怎样改变袋子中黄球、红球、蓝球的个数,
使摸到这三种颜色的球的可能性相等?
(1)能事先确定摸到的这个球的颜色吗?
(2)你认为摸到哪种颜色的球的可能性最大?
不能确定.
摸到黄球的可能性最大.
只要使得袋子中蓝球、黄球、红球的个数相等.
可能性的大小
巩固练习
1.如图,转盘中8个扇形的面积都相等,任意转
动转盘1次,当转盘停止转动时,估计下列事件
发生的可能性的大小,并将这些事件的序号
按发生的可能性从小到大的顺序排列:
(1)指针落在标有5的区域内;
(2)指针落在标有10的区域内;
(3)指针落在标有偶数或奇数的区域内;
(4)指针落在标有奇数的区域内.
按发生的可能性从小到大的顺序排列为:(2)<(1)<(4)<(3)
1
2
3
4
5
6
7
8
不可能事件,它的概率为0
必然事件,它的概率为1
发生的可能性较大
发生的可能性较小
知识回顾
频率与概率
(1)通常,在多次重复实验中,一个随机事件发生的频
率会在某一个常数附近摆动,且趋于稳定,这个性质称
为 频率的稳定性.
(2)用频率估计一个随机事件发生的概率,通常要经历“试验并收集、整理、描述数据——计算频率——估计概
率”的过程.(注意:这里的“试验”,必须在相同条件
下进行,且试验的次数要足够多.)
例3 一只不透明的袋子中装有若干个白球和其他颜色的球,这些球除颜色外都相同.每次从袋子中摸出一个球,然后放回摇匀再摸,在摸球实验中得到下列表中的部分数据:
摸球次数 40 80 400 600 800 1000 1200 1500
摸出白球的频数 14 26 128 198 267 399 500
摸出白球的频率 0.325 0.320 0.330 0.334 0.332 0.333 0.333
(1)请将表补充完整;
332
0.350
14÷40=0.350
频率与概率
典例分析
1 000×0.332=332
频率与概率
典例分析
(2)画出“摸出白球”的频率折线统计图,得摸出白球的概率估计值
是________;(精确到到0.01)
(3)若袋中共有100个球,则袋中可能有____个白球.
0.33
100×0.33=33
33
巩固练习
频率与概率
1.小杨、小刚用摸球游戏决定谁去看电影,袋中有1个红球和1个白球(除颜色不同外其余相同),得到红球为“看”,得到白球为“不看”,小杨先摸,另一个球留给小刚,这个游戏对双方是 . (填“公平”或“不公平”)
2.在一个有10万人的小镇上,随机调查了2000人,其中有400人看中央电视台的早间新闻,在该镇随便问一人,他看中央电视台早间新闻的概率大约是 .
公平
0.2
巩固练习
频率与概率
3.某次活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.表格是此次活动中的一组统计数据:
转动转盘的次数n 100 200 300 400 500 1000
落在“书画”区域的次数m 60 122 180 242 a 604
落在“书画”区域的频率 0.60 0.61 0.60 b 0.59 0.604
巩固练习
频率与概率
(1)完成上述表格:a = ;b = ;
(2)请估计当n很大时,频率将会接近 ,假如你去转动该转
盘一次,获得“书画”的概率大约是 .(结果全部精确到0.1)
295
0.605
0.6
0.6
巩固练习
频率与概率
4.某批乒乓球的质量检验结果如下:
抽取的乒乓球数n 50 100 200 500 1 000 1 500 2 000
优等品的频数m 48 95 188 471 946 1426 1898
优等品的频率m/n(精确到0.001)
0.960
0.950 0.940 0.942 0.946 0.951 0.949
(1)请将上表补充完整;
巩固练习
频率与概率
(2)画出优等品频率的折线统计图;
(3)从这批乒乓球中,任意抽取的一只乒乓球是优等品的概率的估计值是_________;(精确到0.01)
0.95
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
