2021-2022学年人教版九年级数学下册第28章锐角三角函数 教材分析课件(共30张PPT)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第28章锐角三角函数 教材分析课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 16:50:43 | ||
图片预览







文档简介
(共30张PPT)
第二十八章《锐角三角函数》教材分析
2022.2
初
中
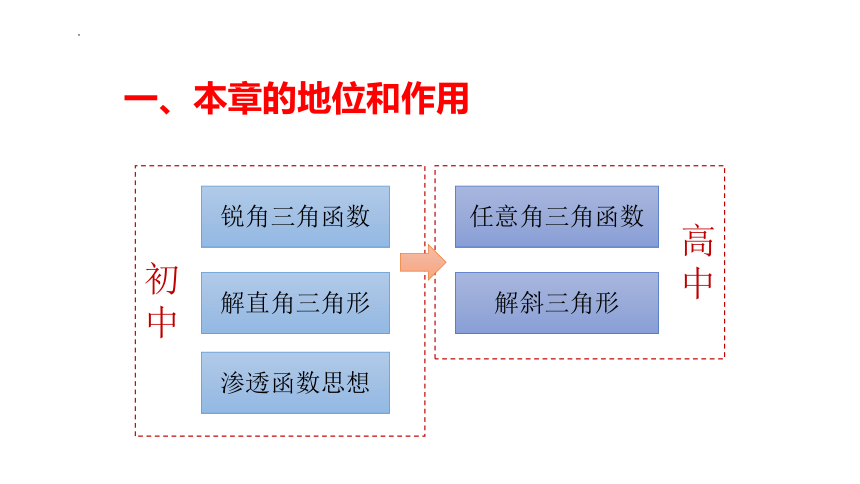
一、本章的地位和作用
锐角三角函数
解直角三角形
任意角三角函数
解斜三角形
高
中
渗透函数思想
初
中
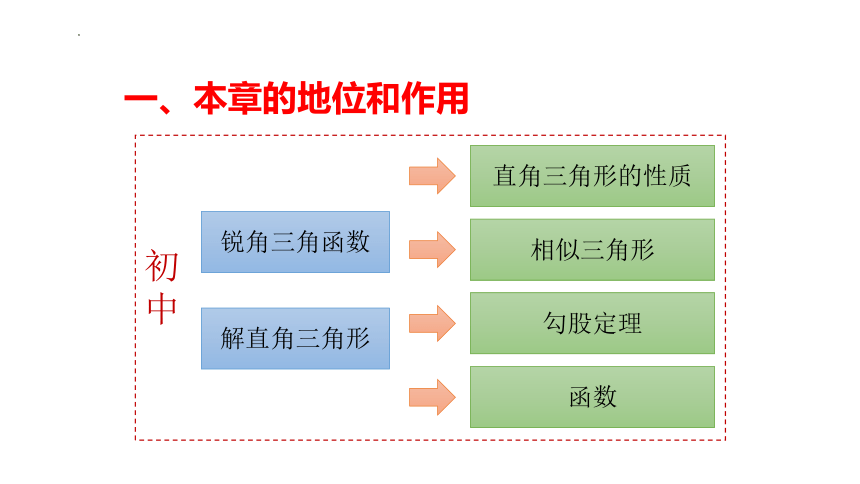
锐角三角函数
解直角三角形
直角三角形的性质
相似三角形
勾股定理
函数
一、本章的地位和作用
(1)利用相似的直角三角形,探索并认识锐角三角函数(sinA,cosA,tanA);理解锐角三角函数的概念;知道30°,45°,60°的三角函数值.
(2)会使用计算器求已知锐角的三角函数值,以及求已知三角函数值对应的锐角.
(3)能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
二、本章教学目标
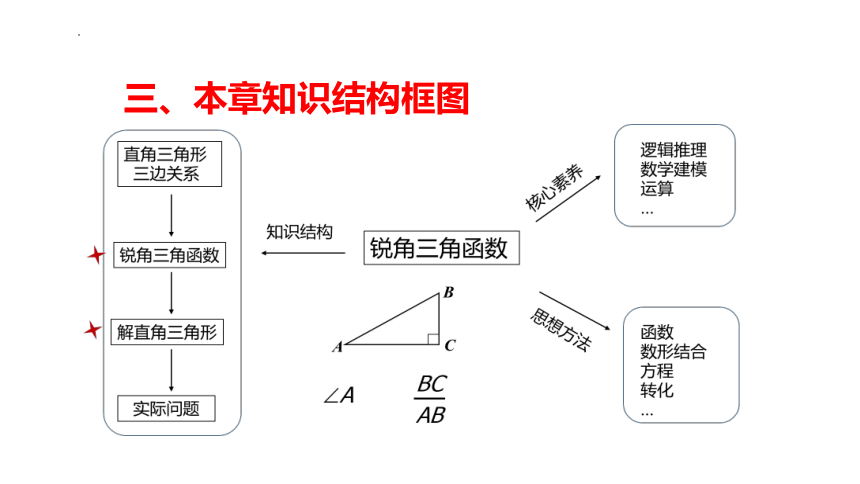
教学重、难点
重点: 锐角三角函数的概念;解直角三角形.
难点: 理解锐角三角函数的概念;综合运用锐角三角函数、勾股定理等知识解直角三角形,进而解决有关问题.
三、本章知识结构框图
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
四、本章教学建议
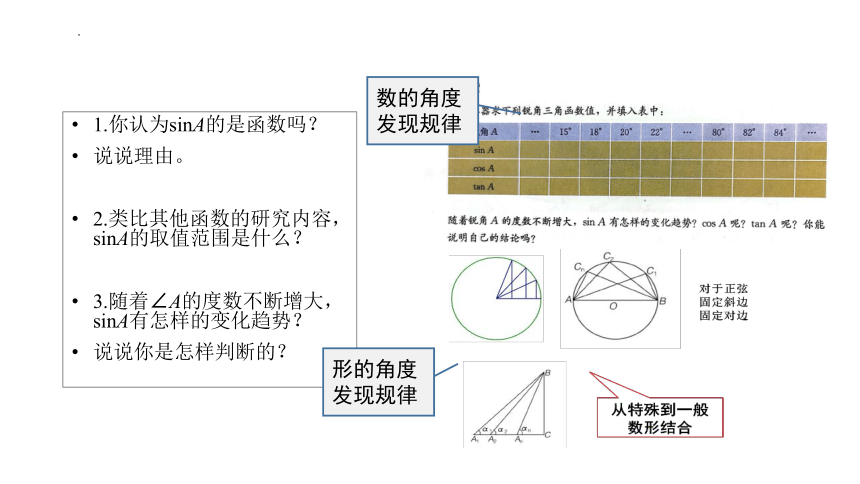
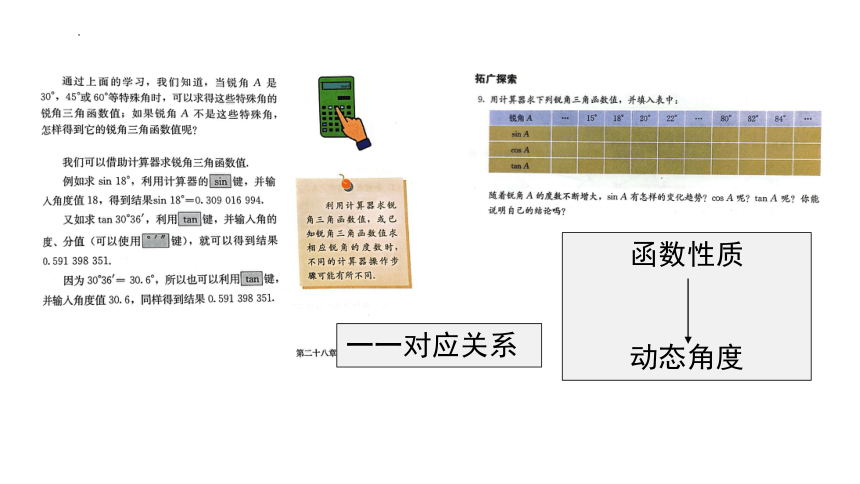
1.你认为sinA的是函数吗?
说说理由。
2.类比其他函数的研究内容,sinA的取值范围是什么?
3.随着∠A的度数不断增大, sinA有怎样的变化趋势?
说说你是怎样判断的?
数的角度发现规律
形的角度发现规律
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
四、本章教学建议
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
(3)发挥计算器的作用
四、本章教学建议
一一对应关系
函数性质
动态角度
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
(3)发挥计算器的作用
(4)渗透思想,重视数学思维
四、本章教学建议
特殊到一般
类比学习
数形结合
数学建模
核心思想
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
(3)发挥计算器的作用
(4)渗透思想,重视数学思维
(5)知识综合,关注知识联系
四、本章教学建议
锐角三角函数
相似
勾股定理
课时安排:
28.1 锐角三角函数 5课时
28.1.1 锐角三角函数定义 2课时
28.1.2 特殊角的三角函数值 1课时
28.1.3 用计算器求锐角三角函数值 1课时 *数学活动1
习题课及讲评 1课时
28.2 解直角三角形及其应用 4课时
28.2.1 解直角三角形 1课时
28.2.2 应用举例 2课时 *数学活动2
习题课及讲评 1课时
数学活动和小结 1-2课时
例1、已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D.
(i)若AD=3,BD=1,求解△ABC;
(ii)若AD=h,∠ACD=β,求解△ABC;
(iii)若AD:BD=3:1,求∠A;
(iv)sin∠BCD= ,CB=4,求AC的长.
等角的同名三角函数值相等
射影定理的渗透
五、典型例题分析
例2、如图,已知在△ABC中,AB=BC=5,tan∠ABC=,.
①求AC的长;
②设边BC的垂直平分线与边AB的交点为点D,
求的值.
思考:若将“AB=BC=5”改为“AB=BC”,还能求出的值吗?
例3、如图,在矩形ABCD 中, AB=8,BC=12,E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F上,连接FC,则 的值为 .
多角度分析问题
作垂
勾股求线段长
利用定义得到答案
方法1:
方法2:
等角的转化
例4、如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得A的俯角β=45°,已知塔高BC=60米,求山高.
解:∵俯角β=45°,
∴设AD=DC=x.
∵俯角α=60°,
∴tan∠ABD=tan30°=
∴ x=30+30 (米)
答: 山高(30+30) 米.
已知直角三角形两条边关系
方程思想
例4、如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得A的俯角β=45°,已知塔高BC=60米,求山高.
过程程序化
分析问题结构
抽象成数学问题
数与形之间的相互转化
获得答案
鼓励多种方法解决问题
比较方法的优劣,寻求优化的解法
过程程序化
形成技能
特殊角的三角函数值计算
(2021) 17.计算:
(2020) 17.计算:
六、中考链接
tanG=tan∠ABO
找等角改变位置
G
O
(2021北京22)如图,在四边形ABCD中,∠ACB=∠CAD=90°,
点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,cosB= ,求BF和AD的长.
隐含了边角关系
(2020)23.如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)求证:∠ADC=∠AOF;
(2)若sinC,BD=8,求EF的长.
利用角表示边
相似
(2020)28.(2)若点A,B都在直线yx+2上,记线段AB到⊙O的“平移距离”为d1,求d1的最小值;
60°
七、拓展
求15°角的三角函数(以tan 15°为例).
方法1:
.
方法2:
利用45°和30°构造15°
利用特殊角三角函数得到BE和AE的比值.
方法3 : 如图,在△ABD中,BC⊥AD于点C,∠A=∠ABC=45°,
∠DBC=30°,CD=1,BD=2,AC=BC= ,AB=.
作DE⊥AB于点E.
等腰Rt△ADE
AE=DE的长
BE的长
求出tan 15°
感谢聆听,
恳请批评指正!
第二十八章《锐角三角函数》教材分析
2022.2
初
中
一、本章的地位和作用
锐角三角函数
解直角三角形
任意角三角函数
解斜三角形
高
中
渗透函数思想
初
中
锐角三角函数
解直角三角形
直角三角形的性质
相似三角形
勾股定理
函数
一、本章的地位和作用
(1)利用相似的直角三角形,探索并认识锐角三角函数(sinA,cosA,tanA);理解锐角三角函数的概念;知道30°,45°,60°的三角函数值.
(2)会使用计算器求已知锐角的三角函数值,以及求已知三角函数值对应的锐角.
(3)能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题.
二、本章教学目标
教学重、难点
重点: 锐角三角函数的概念;解直角三角形.
难点: 理解锐角三角函数的概念;综合运用锐角三角函数、勾股定理等知识解直角三角形,进而解决有关问题.
三、本章知识结构框图
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
四、本章教学建议
1.你认为sinA的是函数吗?
说说理由。
2.类比其他函数的研究内容,sinA的取值范围是什么?
3.随着∠A的度数不断增大, sinA有怎样的变化趋势?
说说你是怎样判断的?
数的角度发现规律
形的角度发现规律
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
四、本章教学建议
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
(3)发挥计算器的作用
四、本章教学建议
一一对应关系
函数性质
动态角度
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
(3)发挥计算器的作用
(4)渗透思想,重视数学思维
四、本章教学建议
特殊到一般
类比学习
数形结合
数学建模
核心思想
(1)加强锐角三角函数概念的探究过程,揭示概念的内涵
(2)加强运算、推理等能力的培养
(3)发挥计算器的作用
(4)渗透思想,重视数学思维
(5)知识综合,关注知识联系
四、本章教学建议
锐角三角函数
相似
勾股定理
课时安排:
28.1 锐角三角函数 5课时
28.1.1 锐角三角函数定义 2课时
28.1.2 特殊角的三角函数值 1课时
28.1.3 用计算器求锐角三角函数值 1课时 *数学活动1
习题课及讲评 1课时
28.2 解直角三角形及其应用 4课时
28.2.1 解直角三角形 1课时
28.2.2 应用举例 2课时 *数学活动2
习题课及讲评 1课时
数学活动和小结 1-2课时
例1、已知,如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D.
(i)若AD=3,BD=1,求解△ABC;
(ii)若AD=h,∠ACD=β,求解△ABC;
(iii)若AD:BD=3:1,求∠A;
(iv)sin∠BCD= ,CB=4,求AC的长.
等角的同名三角函数值相等
射影定理的渗透
五、典型例题分析
例2、如图,已知在△ABC中,AB=BC=5,tan∠ABC=,.
①求AC的长;
②设边BC的垂直平分线与边AB的交点为点D,
求的值.
思考:若将“AB=BC=5”改为“AB=BC”,还能求出的值吗?
例3、如图,在矩形ABCD 中, AB=8,BC=12,E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F上,连接FC,则 的值为 .
多角度分析问题
作垂
勾股求线段长
利用定义得到答案
方法1:
方法2:
等角的转化
例4、如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得A的俯角β=45°,已知塔高BC=60米,求山高.
解:∵俯角β=45°,
∴设AD=DC=x.
∵俯角α=60°,
∴tan∠ABD=tan30°=
∴ x=30+30 (米)
答: 山高(30+30) 米.
已知直角三角形两条边关系
方程思想
例4、如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得A的俯角β=45°,已知塔高BC=60米,求山高.
过程程序化
分析问题结构
抽象成数学问题
数与形之间的相互转化
获得答案
鼓励多种方法解决问题
比较方法的优劣,寻求优化的解法
过程程序化
形成技能
特殊角的三角函数值计算
(2021) 17.计算:
(2020) 17.计算:
六、中考链接
tanG=tan∠ABO
找等角改变位置
G
O
(2021北京22)如图,在四边形ABCD中,∠ACB=∠CAD=90°,
点E在BC上,AE∥DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE=5,cosB= ,求BF和AD的长.
隐含了边角关系
(2020)23.如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)求证:∠ADC=∠AOF;
(2)若sinC,BD=8,求EF的长.
利用角表示边
相似
(2020)28.(2)若点A,B都在直线yx+2上,记线段AB到⊙O的“平移距离”为d1,求d1的最小值;
60°
七、拓展
求15°角的三角函数(以tan 15°为例).
方法1:
.
方法2:
利用45°和30°构造15°
利用特殊角三角函数得到BE和AE的比值.
方法3 : 如图,在△ABD中,BC⊥AD于点C,∠A=∠ABC=45°,
∠DBC=30°,CD=1,BD=2,AC=BC= ,AB=.
作DE⊥AB于点E.
等腰Rt△ADE
AE=DE的长
BE的长
求出tan 15°
感谢聆听,
恳请批评指正!
