2021—2022学年人教版数学七年级下册第五章相交线与平行线 小结与复习课件(共18张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学七年级下册第五章相交线与平行线 小结与复习课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 185.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览

文档简介
(共18张PPT)
小结与复习
第五章 相交线与平行线
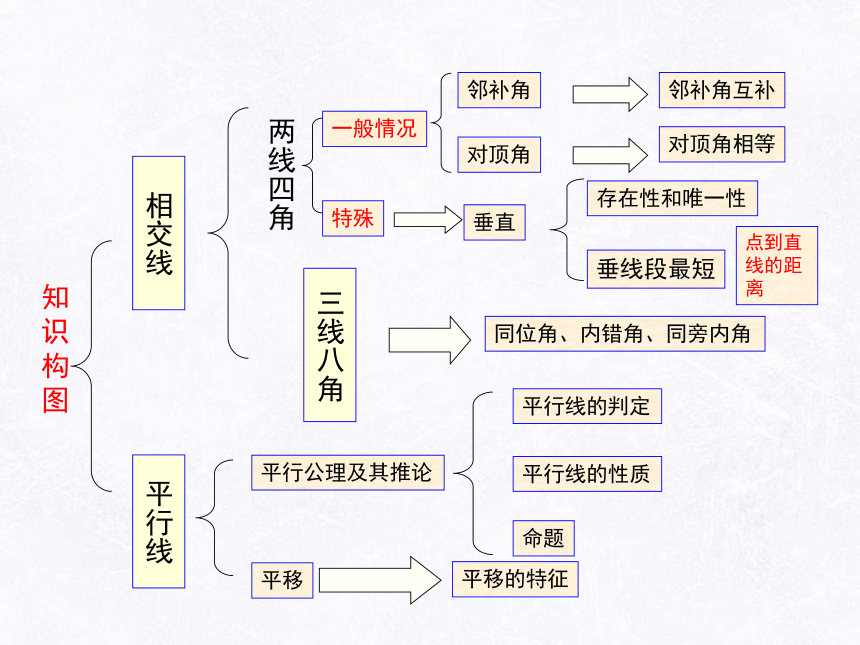
相交线
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
平移
平移的特征
命题
知识构图
两线四角
三线八角
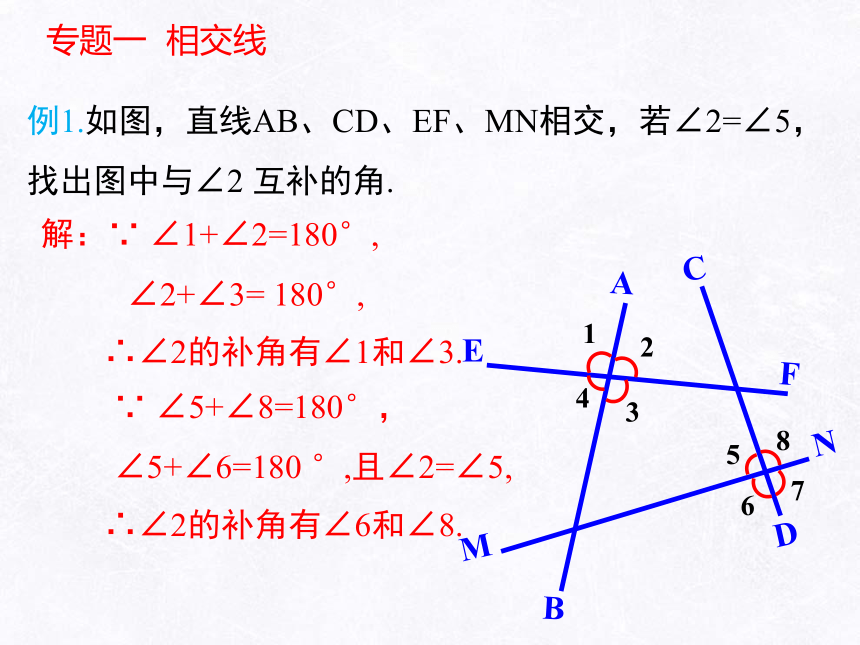
专题一 相交线
例1.如图,直线AB、CD、EF、MN相交,若∠2=∠5,
找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ ∠1+∠2=180°,
∠2+∠3= 180°,
∴∠2的补角有∠1和∠3.
∵ ∠5+∠8=180°,
∠5+∠6=180 °,且∠2=∠5,
∴∠2的补角有∠6和∠8.
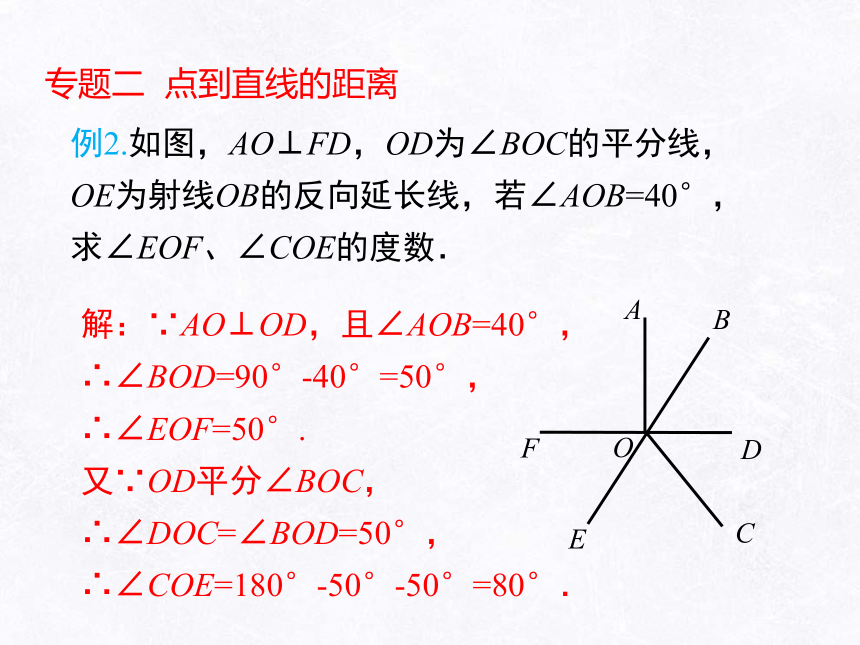
专题二 点到直线的距离
例2.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD,且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
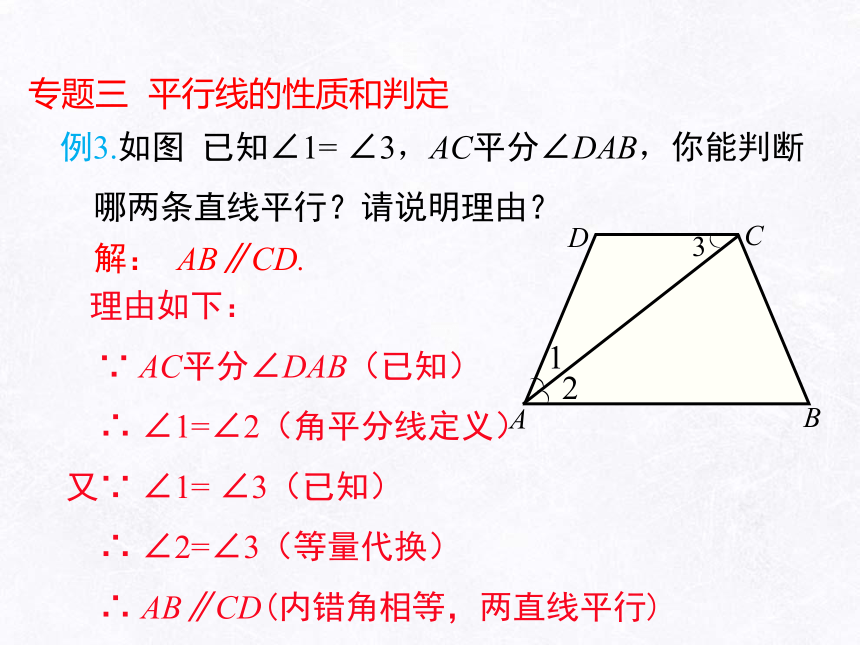
专题三 平行线的性质和判定
理由如下:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
例3.如图 已知∠1= ∠3,AC平分∠DAB,你能判断
哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
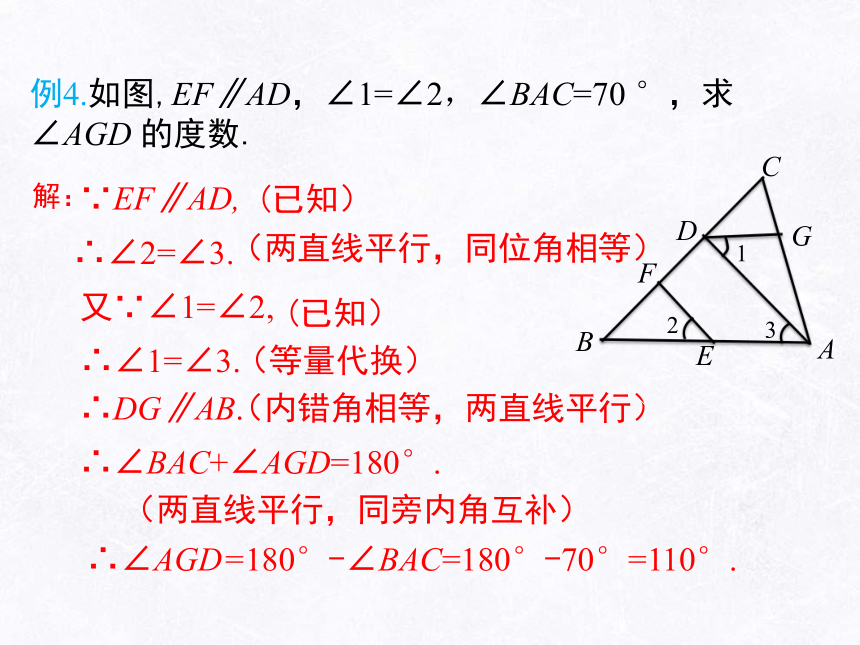
例4.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD 的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
专题四 平移
1m
21m
15m
A
C
D
B
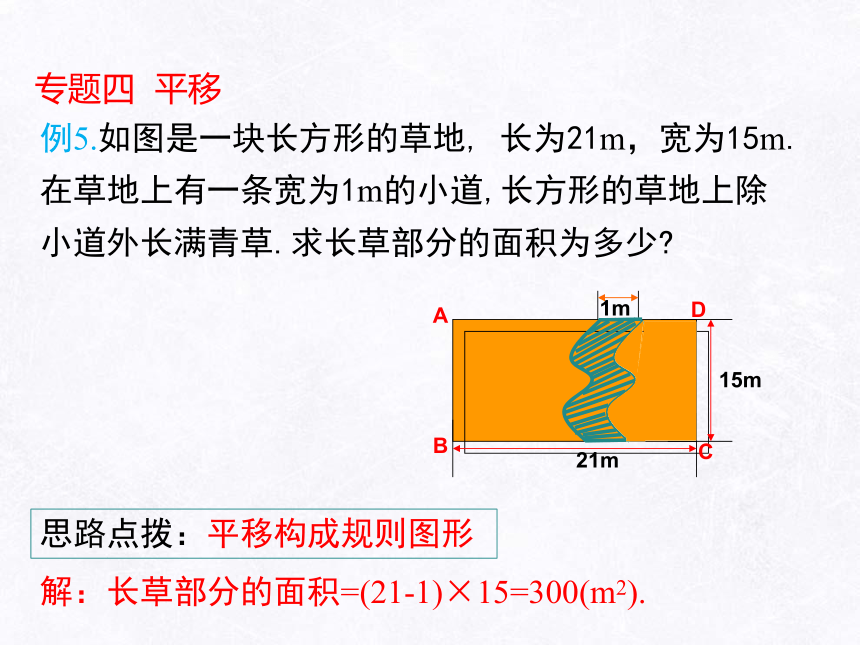
例5.如图是一块长方形的草地, 长为21m,宽为15m.在草地上有一条宽为1m的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
课后跟踪训练
1.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
2.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐50 ,第二次向左拐130
B.第一次向左拐30 ,第二次向右拐30
C.第一次向右拐50 ,第二次向右拐130
D.第一次向左拐50 ,第二次向左拐130
B
4.填空:如图,
(1)∠1= 时,AB∥CD;
(2)AD∥BC时,∠3= .
D
1
2
3
4
5
A
B
C
F
E
∠2
∠5
或∠4
解: ∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( )
5.如图2,若AB∥DE , AC∥DF,试说明∠A+∠D=180°.请补全下面的解答过程,括号内填写依据.
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
6.有这样一道题:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数. 请补全下列解答过程
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
解:过点E作EF//AB.
∵AB//CD(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °.
∴∠AEC=∠1+∠2= °+ ° = °.
7.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
∵∠1=∠2
∴AB∥EF
(内错角相等,两直线平行).
(已知),
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
8.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解:过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
Q
9、如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
解:过点E 向左作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°,
即∠B+∠D+∠DEB=360°.
F
谢谢欣赏!
小结与复习
第五章 相交线与平行线
相交线
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
平移
平移的特征
命题
知识构图
两线四角
三线八角
专题一 相交线
例1.如图,直线AB、CD、EF、MN相交,若∠2=∠5,
找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ ∠1+∠2=180°,
∠2+∠3= 180°,
∴∠2的补角有∠1和∠3.
∵ ∠5+∠8=180°,
∠5+∠6=180 °,且∠2=∠5,
∴∠2的补角有∠6和∠8.
专题二 点到直线的距离
例2.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD,且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
专题三 平行线的性质和判定
理由如下:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD(内错角相等,两直线平行)
例3.如图 已知∠1= ∠3,AC平分∠DAB,你能判断
哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
例4.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD 的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
专题四 平移
1m
21m
15m
A
C
D
B
例5.如图是一块长方形的草地, 长为21m,宽为15m.在草地上有一条宽为1m的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形
解:长草部分的面积=(21-1)×15=300(m2).
课后跟踪训练
1.如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
2.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐50 ,第二次向左拐130
B.第一次向左拐30 ,第二次向右拐30
C.第一次向右拐50 ,第二次向右拐130
D.第一次向左拐50 ,第二次向左拐130
B
4.填空:如图,
(1)∠1= 时,AB∥CD;
(2)AD∥BC时,∠3= .
D
1
2
3
4
5
A
B
C
F
E
∠2
∠5
或∠4
解: ∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( )
5.如图2,若AB∥DE , AC∥DF,试说明∠A+∠D=180°.请补全下面的解答过程,括号内填写依据.
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
6.有这样一道题:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数. 请补全下列解答过程
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
解:过点E作EF//AB.
∵AB//CD(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °.
∴∠AEC=∠1+∠2= °+ ° = °.
7.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
∵∠1=∠2
∴AB∥EF
(内错角相等,两直线平行).
(已知),
∵AB⊥BF,CD⊥BF,
∴AB∥CD
∴EF∥CD
∴ ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,同位角相等).
8.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
解:过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
Q
9、如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
解:过点E 向左作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°,
即∠B+∠D+∠DEB=360°.
F
谢谢欣赏!
