青岛版六年级数学上册第三单元比复习提纲
图片预览

文档简介
六年级数学上册第三单元
《比》复习提纲
学习目标
1、在解决实际问题的过程中,理解比的意义,会求比值;掌握比的基本性质,会化简比。
2、经历比的意义和比的基本性质的探索过程,提高比较、类推能力,体验划归的数学方法。
3、在解决有关按比例分配的实际问题中,感受比在生活中的应用,体验解决问题策略的多样性。
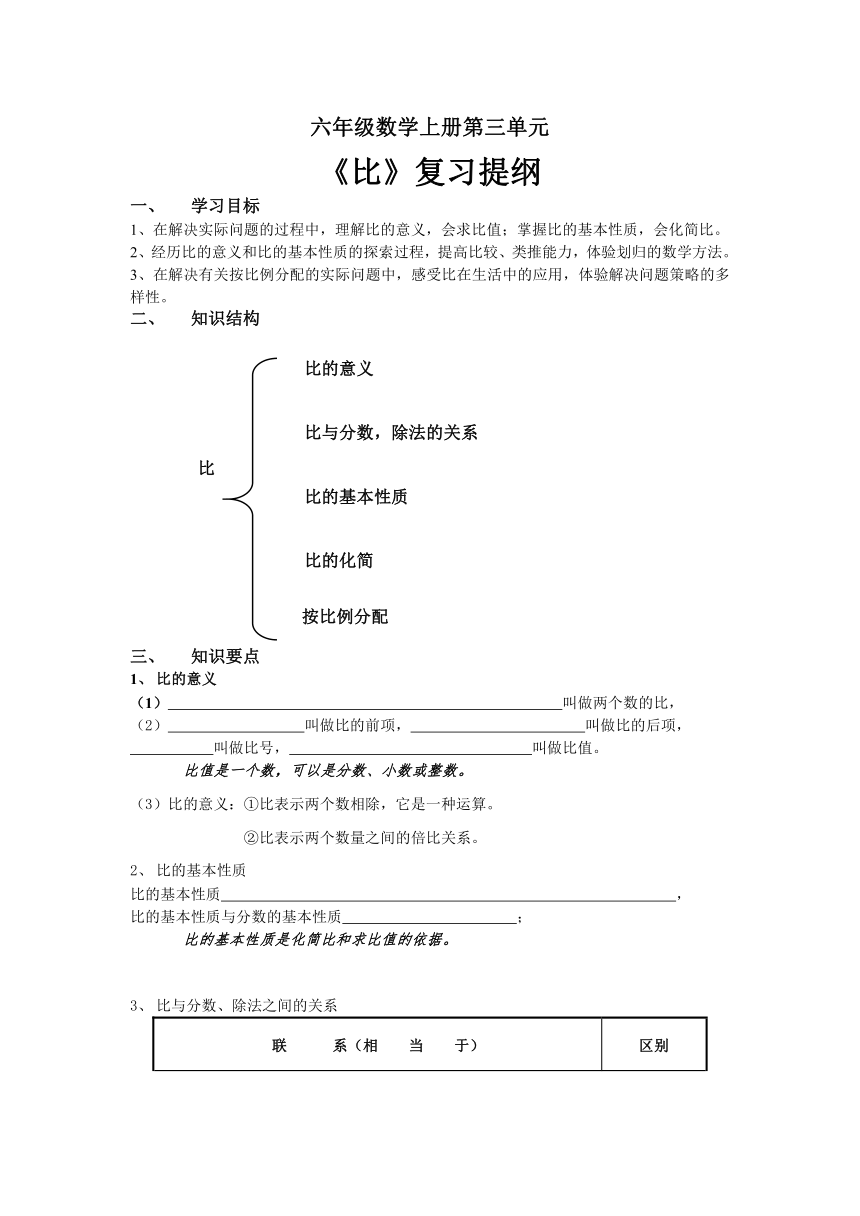
知识结构
知识要点
比的意义
(1) 叫做两个数的比,
(2) 叫做比的前项, 叫做比的后项,
叫做比号, 叫做比值。
比值是一个数,可以是分数、小数或整数。
(3)比的意义:①比表示两个数相除,它是一种运算。
②比表示两个数量之间的倍比关系。
比的基本性质
比的基本性质 ,
比的基本性质与分数的基本性质 ;
比的基本性质是化简比和求比值的依据。
比与分数、除法之间的关系
联 系(相 当 于)
区别
比
?比的前项
?比的后项
?:比号
?比值
?
除法
?
?
?
?
?
分数
?
?
?
?
?
比的化简
最简整数比:比的前项和后项都是整数,且比的前项和后项的最大公因数是1,这样的比叫做最简整数比。
整数比的化简可以用比的前后项都除以它们的最大公因数,得到最简整数比。
分数比的化简可以用比的前后项都乘它们分母的最小公倍数,从而得到整数比,再进一步化简成最简整数比
小数比的化简可以用比的前后项都扩大相同的倍数,从而得到整数比,再化简成最简整数比。
按要求完成下列各题
求比值
化简比
0.124千克:50克 米:20厘米 平方米:90平方分米
小结:
①两个同类量相比,必须先把单位统一。
②两个同类量相比,比值不能带有单位。
③两个相关联的非同类量相比,可以表示一个新的量。(如路程:时间=速度)。
按比例分配
在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫做按比例分配。
例1 一种糖水是糖与水按1:9的比例配制而成的,要配制这种糖水2千克,需要糖和水各多少千克?
例2一个三角形的三个内角的度数比是1:2:3,这是一个什么三角形?为什么?
例3用一段铁丝围成一个三角形,一条边的长度比是4:5:7,已知最长边是28厘米,这段铁丝有多长?
拓展提高
单位“1”的转化
例:甲数是乙数的,乙数是丙数的,求这三个数的连比。
分析:这里 “乙数是丙数的”的单位“1”是 ,即“乙数=丙数×”,我们可以把它变形为“乙数×=丙数”,即“丙数是乙数的”,这样就和甲数是乙数的中的单位“1”一致了。
解:因为乙数是丙数的,所以丙数是乙数的 ,
所以甲数:乙数:丙数= = 。
2.“中间量”的利用
例:甲数是乙数的,乙数是丙数的,求这三个数的连比。
分析:由甲数是乙数的,可得“甲数:乙数=3:5”,由乙数是丙数的可得“乙数:丙数=4:7”,这里乙数作为“中间量”所占的份数不同,可利用比的基本性质使它变成相同的份数就行了。
解:因为甲数是乙数的,乙数是丙数的
所以甲数:乙数= = ,
乙数:丙数= = ,
所以甲数:乙数:丙数= 。
3. “特殊值”法
例:现有两杯同样质量盐水,盐和水的比例分别是2:8和1:7,把这两杯盐水混合后盐和水的比是多少?
分析:这两杯盐水的质量不知道,可以给出一个假定的值,如100克,这样就可以求出第一杯中含盐量为(克),第二杯中含盐量为(克),那么混合后盐:水=(20+12.5)(80+87.5)=32.5:167.5=13:67
解:
4. 借助“线段图”分析
例:已知甲乙两数的和为360,且甲数的等于乙数的,求甲乙两数分别是多少。
分析:由甲数的等于乙数的可以画出线段图,
由线段图可以看出甲数:乙数=5:7,从而可得
甲数占总数的 ,乙数占总数的 ;
解:
《比》复习提纲
学习目标
1、在解决实际问题的过程中,理解比的意义,会求比值;掌握比的基本性质,会化简比。
2、经历比的意义和比的基本性质的探索过程,提高比较、类推能力,体验划归的数学方法。
3、在解决有关按比例分配的实际问题中,感受比在生活中的应用,体验解决问题策略的多样性。
知识结构
知识要点
比的意义
(1) 叫做两个数的比,
(2) 叫做比的前项, 叫做比的后项,
叫做比号, 叫做比值。
比值是一个数,可以是分数、小数或整数。
(3)比的意义:①比表示两个数相除,它是一种运算。
②比表示两个数量之间的倍比关系。
比的基本性质
比的基本性质 ,
比的基本性质与分数的基本性质 ;
比的基本性质是化简比和求比值的依据。
比与分数、除法之间的关系
联 系(相 当 于)
区别
比
?比的前项
?比的后项
?:比号
?比值
?
除法
?
?
?
?
?
分数
?
?
?
?
?
比的化简
最简整数比:比的前项和后项都是整数,且比的前项和后项的最大公因数是1,这样的比叫做最简整数比。
整数比的化简可以用比的前后项都除以它们的最大公因数,得到最简整数比。
分数比的化简可以用比的前后项都乘它们分母的最小公倍数,从而得到整数比,再进一步化简成最简整数比
小数比的化简可以用比的前后项都扩大相同的倍数,从而得到整数比,再化简成最简整数比。
按要求完成下列各题
求比值
化简比
0.124千克:50克 米:20厘米 平方米:90平方分米
小结:
①两个同类量相比,必须先把单位统一。
②两个同类量相比,比值不能带有单位。
③两个相关联的非同类量相比,可以表示一个新的量。(如路程:时间=速度)。
按比例分配
在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配,这种分配方法通常叫做按比例分配。
例1 一种糖水是糖与水按1:9的比例配制而成的,要配制这种糖水2千克,需要糖和水各多少千克?
例2一个三角形的三个内角的度数比是1:2:3,这是一个什么三角形?为什么?
例3用一段铁丝围成一个三角形,一条边的长度比是4:5:7,已知最长边是28厘米,这段铁丝有多长?
拓展提高
单位“1”的转化
例:甲数是乙数的,乙数是丙数的,求这三个数的连比。
分析:这里 “乙数是丙数的”的单位“1”是 ,即“乙数=丙数×”,我们可以把它变形为“乙数×=丙数”,即“丙数是乙数的”,这样就和甲数是乙数的中的单位“1”一致了。
解:因为乙数是丙数的,所以丙数是乙数的 ,
所以甲数:乙数:丙数= = 。
2.“中间量”的利用
例:甲数是乙数的,乙数是丙数的,求这三个数的连比。
分析:由甲数是乙数的,可得“甲数:乙数=3:5”,由乙数是丙数的可得“乙数:丙数=4:7”,这里乙数作为“中间量”所占的份数不同,可利用比的基本性质使它变成相同的份数就行了。
解:因为甲数是乙数的,乙数是丙数的
所以甲数:乙数= = ,
乙数:丙数= = ,
所以甲数:乙数:丙数= 。
3. “特殊值”法
例:现有两杯同样质量盐水,盐和水的比例分别是2:8和1:7,把这两杯盐水混合后盐和水的比是多少?
分析:这两杯盐水的质量不知道,可以给出一个假定的值,如100克,这样就可以求出第一杯中含盐量为(克),第二杯中含盐量为(克),那么混合后盐:水=(20+12.5)(80+87.5)=32.5:167.5=13:67
解:
4. 借助“线段图”分析
例:已知甲乙两数的和为360,且甲数的等于乙数的,求甲乙两数分别是多少。
分析:由甲数的等于乙数的可以画出线段图,
由线段图可以看出甲数:乙数=5:7,从而可得
甲数占总数的 ,乙数占总数的 ;
解:
