苏科版七年级数学下册 11.5 用一元一次不等式解决问题 课件(共19张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 11.5 用一元一次不等式解决问题 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 19:54:51 | ||
图片预览





文档简介
(共19张PPT)
11.5 用一元一次不等式解决问题
一、情境创设
七年级上册
第4章一元一次方程
4.1从问题到方程
试一试
一、情境创设
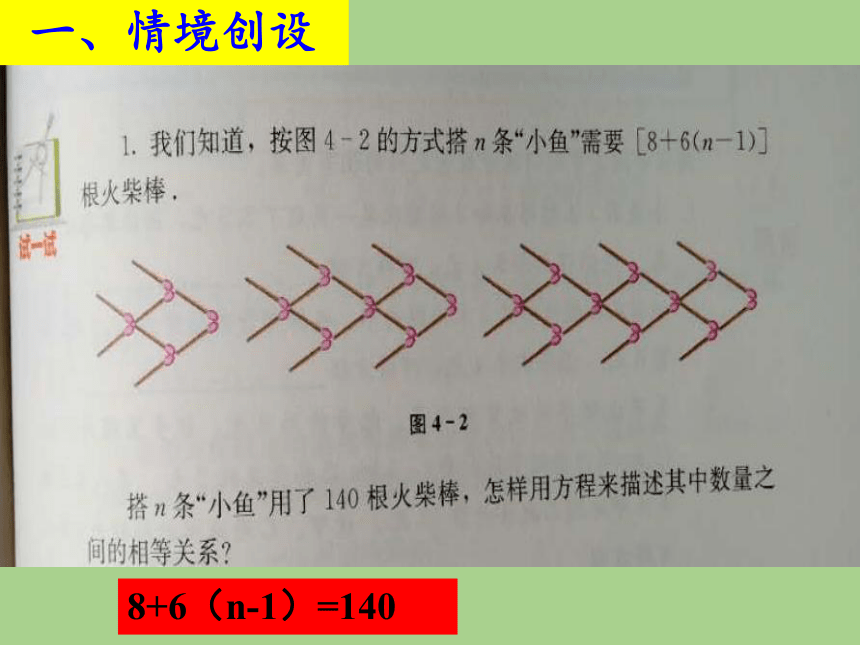
8+6(n-1)=140
用火柴棒按图4-2的方式搭 n 条“小鱼”需要
[8+6(n-1)]根火柴棒。
2、议一议:
用少于50根火柴棒最多能搭多少条小鱼?
一、情境创设
1、搭 n 条“小鱼”用了140根火柴棒,怎样
用方程来描述其中数量之间的相等关系?
【问题1】1、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量为10kg.假设每个苹果的质量为0.25kg。这只纸箱内能装多少个苹果?
二、探索活动
【问题1变式:】2、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg。这只纸箱内能装多少个苹果?
二、探索活动
二、探索活动
【问题1变式:】 3、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg。这只纸箱内最多能装多少个苹果?
解:设这只纸箱内能装x个苹果
根据题意,得:
1+0.25x≤10
解得x≤36
答:这只纸箱内最多能装36个苹果。
将“不超过10kg”,改为“少于10kg”,其他条件不变,则这只纸箱内最多能装多少个苹果?
二、探索活动
二、探索活动
【问题1】1、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量为10kg.假设每个苹果的质量为0.25kg。这只纸箱内能装多少个苹果?
【问题1】3、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg。这只纸箱内最多能装多少个苹果?
比 较
【问题1变式:】 4、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不小于10kg.假设每个苹果的质量为0.25kg。这只纸箱内至少能装多少个苹果?
二、探索活动
追问:你对这题的解有什么想法吗?
用一元一次不等式解决实际问题的一般步骤是:
弄清已知条件、未知条件,找出题中表示实际意义的不等关系,
(1)审:
要抓住题设中的关键字,如“(不)大于、(不)小于、(不)超过、最多(少)、至多(少)”等的含义;
找出题中表示实际
意义的不等关系
例如:
①小明今年x岁,他的年龄不小于12岁.
②一个n边形的内角和超过外角和.
③某种车载客x人,它的最大载客量为14人.
三、总结概括
用一元一次不等式解决实际问题的一般步骤是:
弄清已知条件、未知条件,找出题中表示实际意义的不等关系,
(2)设:设适当的未知数;
(3)列:根据题中的不等关系,列出不等式;
(4)解:求出不等式的解集;
在解集中找出符合题意的答案,并作答.
(1)审:
(5)答:
要抓住题设中的关键字,如“(不)大于、(不)小于、(不)超过、最多(少)、至多(少)” 、至”等的含义;
找出题中表示实际
意义的不等关系
三、总结概括
【例题】某种杜鹃花适宜生长在平均气温为17℃到20℃之间的山区。已知某山区山脚下的平均气温为20℃,并且每上升100m,气温下降0.6℃,要在该山区种植这种杜鹃花,应种在比山脚的海拔最多高多少米的山坡上?
分析
100m
200m
300m
0m
20℃
19.4℃
18.8℃
18.2℃
X m
四、例题教学
某电影院暑假向学生优惠开放,每张票2元.另外,每场次还可以售出每张5元的普通票300张,如果要保持每场次票房收入不低于2000元,那么平均每场次至少应出售学生优惠票多少张?
练习反馈
搭一搭,算一算
按上图的搭法,用4根火柴棒可以搭1个正方形,用____根火柴棒可以搭2个正方形,用____根火柴棒可以搭3个正方形.
一个正方形
两个正方形
三个正方形
…
50根火柴棒
照此搭法,用50根火柴棒最多可以搭出多少个正方形?
7
10
五、数学实验室
…
50根火柴棒
照此搭法,用50根火柴棒最多可以搭出多少个正方形?
解:设用50根火柴棒可搭出x个正方形.
根据题意,得
4 + 3(x-1) ≤ 50
解这个不等式,得
x ≤
答:用50根火柴棒最多可以搭出16个正方形.
一个正方形
两个正方形
三个正方形
请你仿照刚才的实验,搭出一些生活中常见的图形,并提出一个用一元一次不等式解决的问题.
学以致用
一条小鱼
两条小鱼
三条小鱼
实际问题
设未知数
找出不等关系
列不等式
解不等式
结合实际确定答案
用一元一次不等式解实际问题步骤:
数学来源于生活. 数学又服务于生活.
六、课堂小结
课本 P133 1,2
七、布置作业
谢 谢
11.5 用一元一次不等式解决问题
一、情境创设
七年级上册
第4章一元一次方程
4.1从问题到方程
试一试
一、情境创设
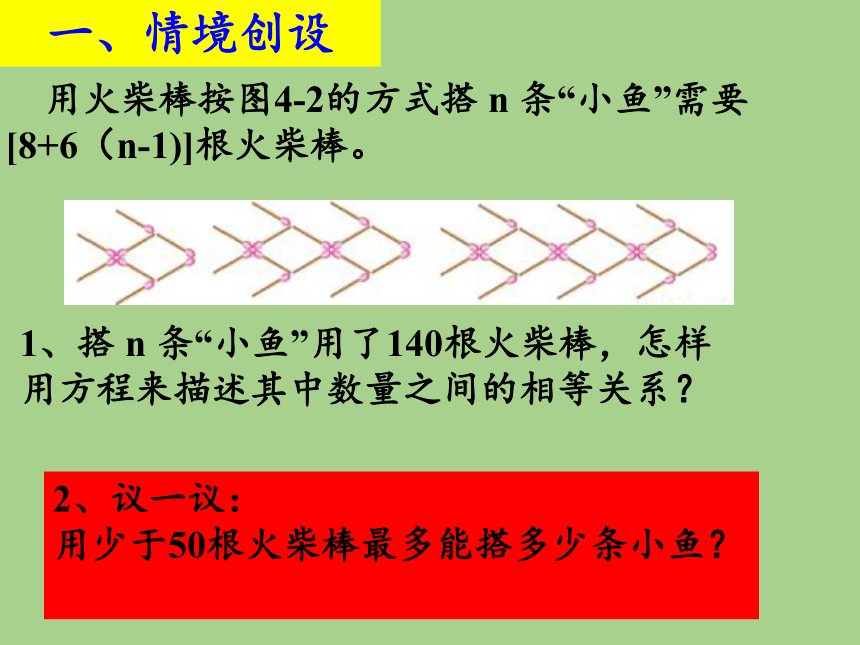
8+6(n-1)=140
用火柴棒按图4-2的方式搭 n 条“小鱼”需要
[8+6(n-1)]根火柴棒。
2、议一议:
用少于50根火柴棒最多能搭多少条小鱼?
一、情境创设
1、搭 n 条“小鱼”用了140根火柴棒,怎样
用方程来描述其中数量之间的相等关系?
【问题1】1、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量为10kg.假设每个苹果的质量为0.25kg。这只纸箱内能装多少个苹果?
二、探索活动
【问题1变式:】2、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg。这只纸箱内能装多少个苹果?
二、探索活动
二、探索活动
【问题1变式:】 3、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg。这只纸箱内最多能装多少个苹果?
解:设这只纸箱内能装x个苹果
根据题意,得:
1+0.25x≤10
解得x≤36
答:这只纸箱内最多能装36个苹果。
将“不超过10kg”,改为“少于10kg”,其他条件不变,则这只纸箱内最多能装多少个苹果?
二、探索活动
二、探索活动
【问题1】1、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量为10kg.假设每个苹果的质量为0.25kg。这只纸箱内能装多少个苹果?
【问题1】3、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不超过10kg.假设每个苹果的质量为0.25kg。这只纸箱内最多能装多少个苹果?
比 较
【问题1变式:】 4、一只纸箱质量为1kg,当放入一些苹果后,箱子和苹果的总质量不小于10kg.假设每个苹果的质量为0.25kg。这只纸箱内至少能装多少个苹果?
二、探索活动
追问:你对这题的解有什么想法吗?
用一元一次不等式解决实际问题的一般步骤是:
弄清已知条件、未知条件,找出题中表示实际意义的不等关系,
(1)审:
要抓住题设中的关键字,如“(不)大于、(不)小于、(不)超过、最多(少)、至多(少)”等的含义;
找出题中表示实际
意义的不等关系
例如:
①小明今年x岁,他的年龄不小于12岁.
②一个n边形的内角和超过外角和.
③某种车载客x人,它的最大载客量为14人.
三、总结概括
用一元一次不等式解决实际问题的一般步骤是:
弄清已知条件、未知条件,找出题中表示实际意义的不等关系,
(2)设:设适当的未知数;
(3)列:根据题中的不等关系,列出不等式;
(4)解:求出不等式的解集;
在解集中找出符合题意的答案,并作答.
(1)审:
(5)答:
要抓住题设中的关键字,如“(不)大于、(不)小于、(不)超过、最多(少)、至多(少)” 、至”等的含义;
找出题中表示实际
意义的不等关系
三、总结概括
【例题】某种杜鹃花适宜生长在平均气温为17℃到20℃之间的山区。已知某山区山脚下的平均气温为20℃,并且每上升100m,气温下降0.6℃,要在该山区种植这种杜鹃花,应种在比山脚的海拔最多高多少米的山坡上?
分析
100m
200m
300m
0m
20℃
19.4℃
18.8℃
18.2℃
X m
四、例题教学
某电影院暑假向学生优惠开放,每张票2元.另外,每场次还可以售出每张5元的普通票300张,如果要保持每场次票房收入不低于2000元,那么平均每场次至少应出售学生优惠票多少张?
练习反馈
搭一搭,算一算
按上图的搭法,用4根火柴棒可以搭1个正方形,用____根火柴棒可以搭2个正方形,用____根火柴棒可以搭3个正方形.
一个正方形
两个正方形
三个正方形
…
50根火柴棒
照此搭法,用50根火柴棒最多可以搭出多少个正方形?
7
10
五、数学实验室
…
50根火柴棒
照此搭法,用50根火柴棒最多可以搭出多少个正方形?
解:设用50根火柴棒可搭出x个正方形.
根据题意,得
4 + 3(x-1) ≤ 50
解这个不等式,得
x ≤
答:用50根火柴棒最多可以搭出16个正方形.
一个正方形
两个正方形
三个正方形
请你仿照刚才的实验,搭出一些生活中常见的图形,并提出一个用一元一次不等式解决的问题.
学以致用
一条小鱼
两条小鱼
三条小鱼
实际问题
设未知数
找出不等关系
列不等式
解不等式
结合实际确定答案
用一元一次不等式解实际问题步骤:
数学来源于生活. 数学又服务于生活.
六、课堂小结
课本 P133 1,2
七、布置作业
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
