5.3反比例函数复习

课件11张PPT。反比例函数复习
复习目标：
1、会用反比例函数的主要性质解决问题
2、能根据题意建立反比例函数模型
3、体会“数形结合”的思想
复习重点：
1、反比例函数的性质
2、用反比例函数的知识解决问题一三二四减小增大轴对称图形中心对称图形3、反比例函数 (k≠0)中比例系数k的几何意义，即过函数图像上任意一点P作x轴、y轴 垂线，设垂足分别为A、B，则所得矩形OAPB的面积为 .一、知识回顾
1、反比例函数：一般地，如果两个变量x、y之间的关系可以表示成y＝ 或 （k为常数，k≠0）的形式，那么称y是x的反比例函数．
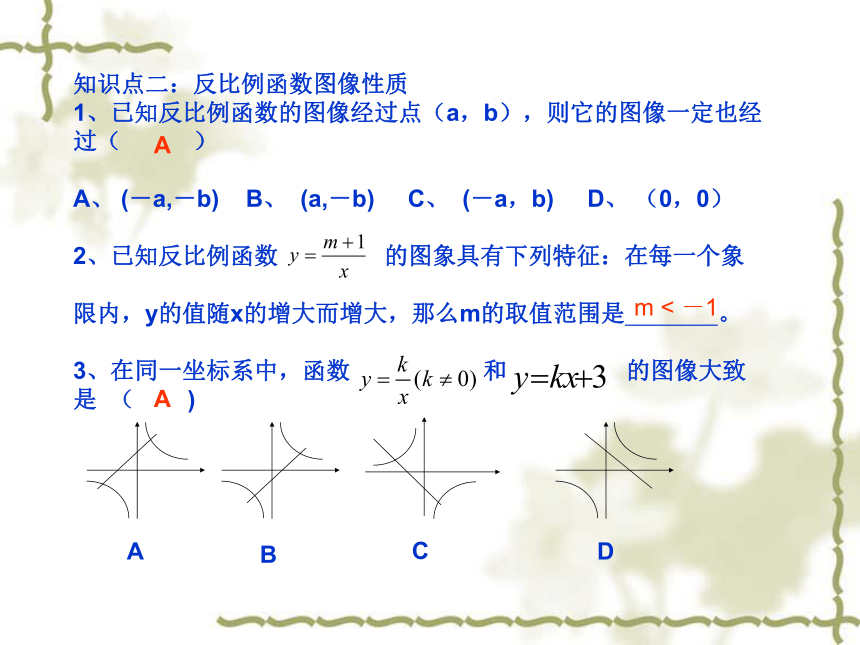
2、反比例函数的图像性质知识点二：反比例函数图像性质
1、已知反比例函数的图像经过点（a，b），则它的图像一定也经
过（　　　）
A、 (－a,－b) B、 (a,－b) C、 (－a，b) D、 （0，0）
2、已知反比例函数 的图象具有下列特征：在每一个象
限内，y的值随x的增大而增大，那么m的取值范围是 。
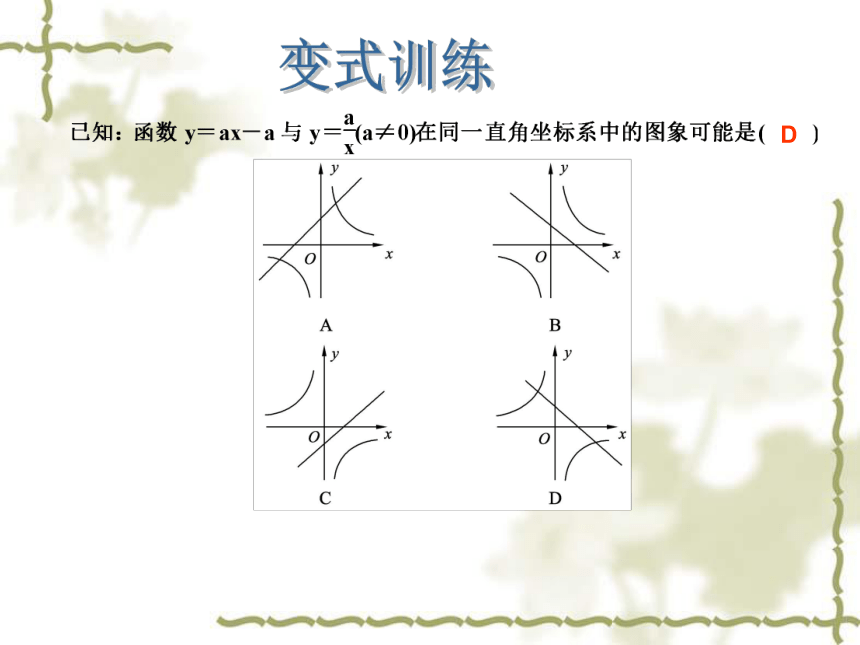
3、在同一坐标系中，函数 和 的图像大致是 （ ) AB CD Am < －1 A变式训练D4、已知反比例函数 ，当m= 时，其图
象的两个分支在第一、三象限内。
5、已知点A（-2，y1）、B（-1，y2）、C（4，y3）都在反比例
函数 的图象上，则（ ）

（A）y1 (C) y31、如图2，若点在反比例函数 的图象上， 轴于M ,

的面积为3，则 ．
2、如图，在函数 的图象上有三点A，B，C过这三个点分别
向x轴、y轴引垂线，过每个点所引的两条垂线与x轴，y轴围成的矩形
的面积分别是S1、S2、S3，则（ ）
A S1>S2>S3 B S11、如图，一次函数 的图象与反比例函数 的图
象交于 两点．
（1）试确定上述反比例函数和一次函数的表达式；
（2）求 的面积．三、课堂小结：
请谈一下你本节课有哪些收获？学而不思则罔思而不学则殆