正多边形中的变式练习
图片预览




文档简介
课件13张PPT。
学而不思则罔,思而不学则殆。
——孔子
正多边形中的变式练习 新城实验学校
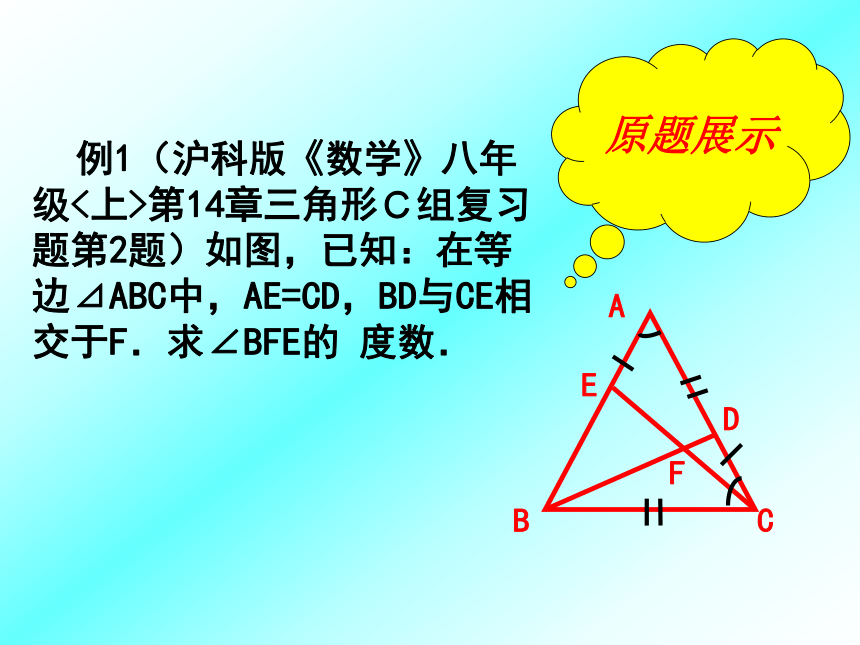
例1(沪科版《数学》八年级<上>第14章三角形C组复习题第2题)如图,已知:在等边⊿ABC中,AE=CD,BD与CE相交于F.求∠BFE的 度数.原题展示 (1)如图,已知:在等边⊿ABC中,
AE=CD,BD与CE相交于F.求证:BD=CE. (3)如图,已知:在等边
⊿ABC中,BD与CE相交于F, .
求证:① BD=CE,②AE=CD .
(2)如图,已知:在等边
⊿ABC中,BD与CE相交于F,
BD=CE.求证:①AE=CD,
② .
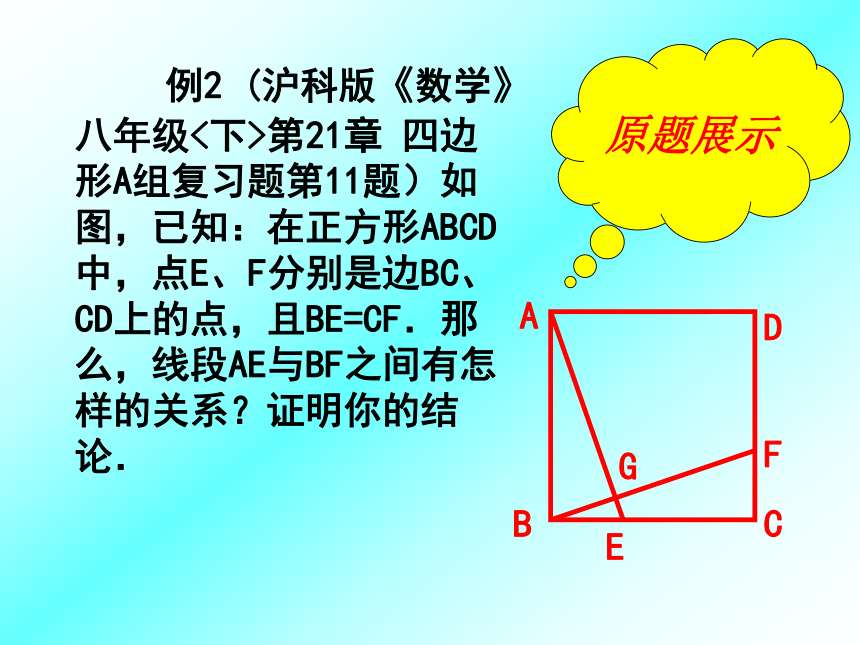
?变式练习 例2 (沪科版《数学》八年级<下>第21章 四边形A组复习题第11题)如图,已知:在正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF.那么,线段AE与BF之间有怎样的关系?证明你的结论.原题展示 如图,已知:在正方形ABCD中,点E、F、G分别是边BC、AB、CD上的点,且AE=FG.那么,线段AE与FG互相垂直吗?证明你的结论.
如图,已知:在正方形ABCD中,点E、F、G、H分别是边AB、CD、AD、BC上的点,且EF=GH.那么,线段EF与GH互相垂直吗?证明你的结论.
变式练习 如图,正五边形 中,点B、C分别是 、 上的点,且 ,那么 和 相等吗? 等于多少度?证明你的结论.拓展与延伸 如图,在正n(n≥3)边形 中,点B、C分别是 、 上的点,且 , 那么 和 相等吗? 等于多少度?证明你的结论.拓展与延伸 问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题: ①如图1,在正三角形ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若 ,则BM=CN. ②如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若 ,则BM=CN. 然后运用类比的思想提出了如下的命题: ③如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若 ,则BM=CN.
任务要求 (1)请你从①、②、③三个命题中选择一个进行证明; (2)请你继续完成下面的探索: ①如图4,在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,问当∠BON等于多少度时,结论BM=CN成立?(不要求证明) ②如图5,在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,当 时,请问结论BM=CN是否还成立?若成立,请给予证明;若不成立,请说明理由.中考链接分享收获 学习的过程就是一个不断地思考与总结的过程。
学而不思则罔,思而不学则殆。
——孔子
正多边形中的变式练习 新城实验学校
例1(沪科版《数学》八年级<上>第14章三角形C组复习题第2题)如图,已知:在等边⊿ABC中,AE=CD,BD与CE相交于F.求∠BFE的 度数.原题展示 (1)如图,已知:在等边⊿ABC中,
AE=CD,BD与CE相交于F.求证:BD=CE. (3)如图,已知:在等边
⊿ABC中,BD与CE相交于F, .
求证:① BD=CE,②AE=CD .
(2)如图,已知:在等边
⊿ABC中,BD与CE相交于F,
BD=CE.求证:①AE=CD,
② .
?变式练习 例2 (沪科版《数学》八年级<下>第21章 四边形A组复习题第11题)如图,已知:在正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF.那么,线段AE与BF之间有怎样的关系?证明你的结论.原题展示 如图,已知:在正方形ABCD中,点E、F、G分别是边BC、AB、CD上的点,且AE=FG.那么,线段AE与FG互相垂直吗?证明你的结论.
如图,已知:在正方形ABCD中,点E、F、G、H分别是边AB、CD、AD、BC上的点,且EF=GH.那么,线段EF与GH互相垂直吗?证明你的结论.
变式练习 如图,正五边形 中,点B、C分别是 、 上的点,且 ,那么 和 相等吗? 等于多少度?证明你的结论.拓展与延伸 如图,在正n(n≥3)边形 中,点B、C分别是 、 上的点,且 , 那么 和 相等吗? 等于多少度?证明你的结论.拓展与延伸 问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题: ①如图1,在正三角形ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若 ,则BM=CN. ②如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若 ,则BM=CN. 然后运用类比的思想提出了如下的命题: ③如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若 ,则BM=CN.
任务要求 (1)请你从①、②、③三个命题中选择一个进行证明; (2)请你继续完成下面的探索: ①如图4,在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,问当∠BON等于多少度时,结论BM=CN成立?(不要求证明) ②如图5,在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,当 时,请问结论BM=CN是否还成立?若成立,请给予证明;若不成立,请说明理由.中考链接分享收获 学习的过程就是一个不断地思考与总结的过程。
