2021-2022学年人教版九年级数学下册28.2.1解直角三角形习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册28.2.1解直角三角形习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 192.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 18:53:34 | ||
图片预览


文档简介
《解直角三角形》习题
一、选择题(每小题5分,共25分)
1.在Rt△ABC中,∠C=90°,AB=12,cos A=,则AC等于( )
A.36 B. C.4 D.
2.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )
A.7sin 35° B. C.7cos35° D.7tan35°
3.在平行四边形ABCD中,已知AB=3cm,BC=4cm,∠B=60°,则S□ABCD等于( )
A.cm2 B.cm2 C.cm2 D.cm2
4.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )
A.25 B. C. D.
(
同学
甲
乙
丙
丁
放出风筝线长(
m)
100
100
95
95
线与地面夹角
30
°
45
°
45
°
60
°
)
第4题图 第5题表
5.身高相等的四名同学甲乙丙丁一起参加风筝比较,四人放出风筝的线长、线与地面的夹角如上表所示(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题5分,共25分)
6.如图,离地面高度为5米的A处引拉线固定电线杆,要使拉线与地面a=37°,工作人员需买拉线的长度约为_____________(精确到米).(sin37°≈0.6,cos37°≈0.8)
第6题图 第7题图 第8题图
7.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE= .
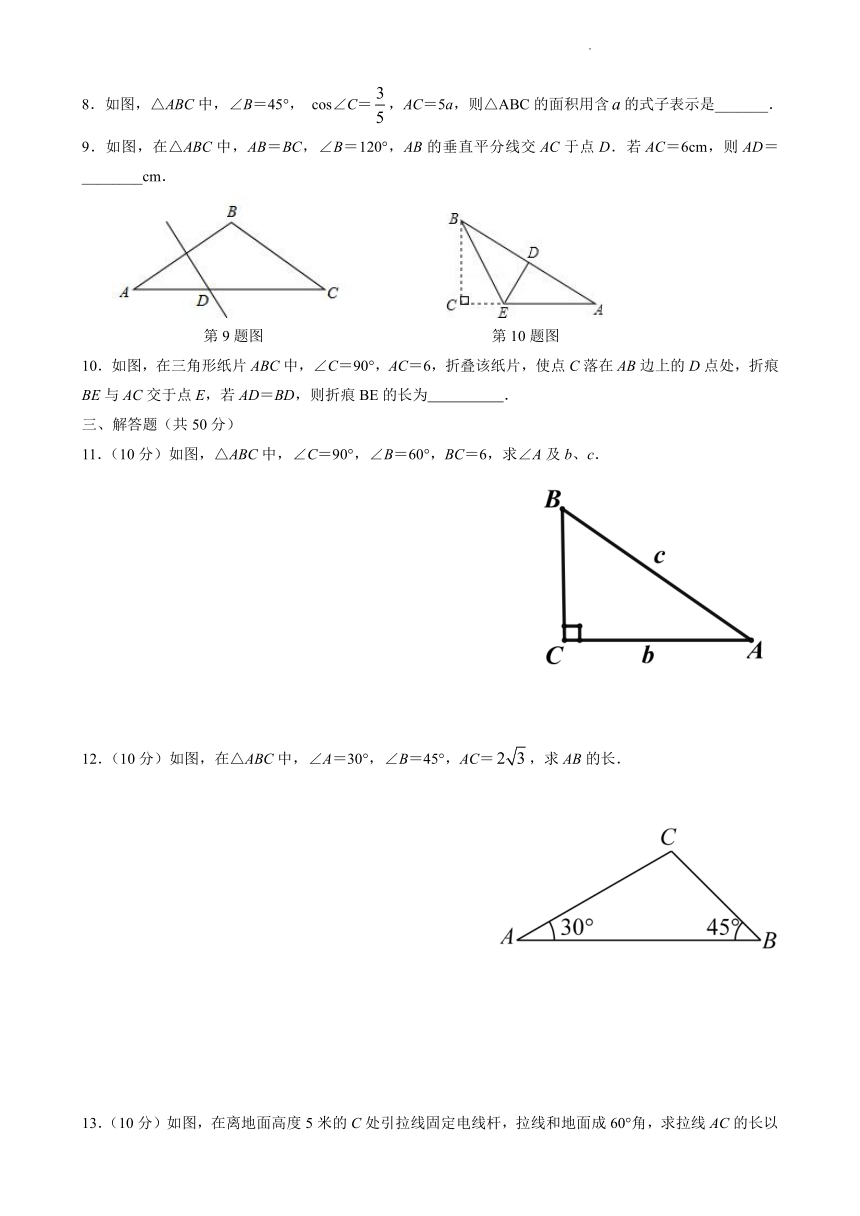
8.如图,△ABC中,∠B=45°, cos∠C=,AC=5a,则△ABC的面积用含的式子表示是_______.
9.如图,在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D.若AC=6cm,则AD=________cm.
第9题图 第10题图
10.如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为 .
三、解答题(共50分)
11.(10分)如图,△ABC中,∠C=90°,∠B=60°,BC=6,求∠A及b、c.
12.(10分)如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长.
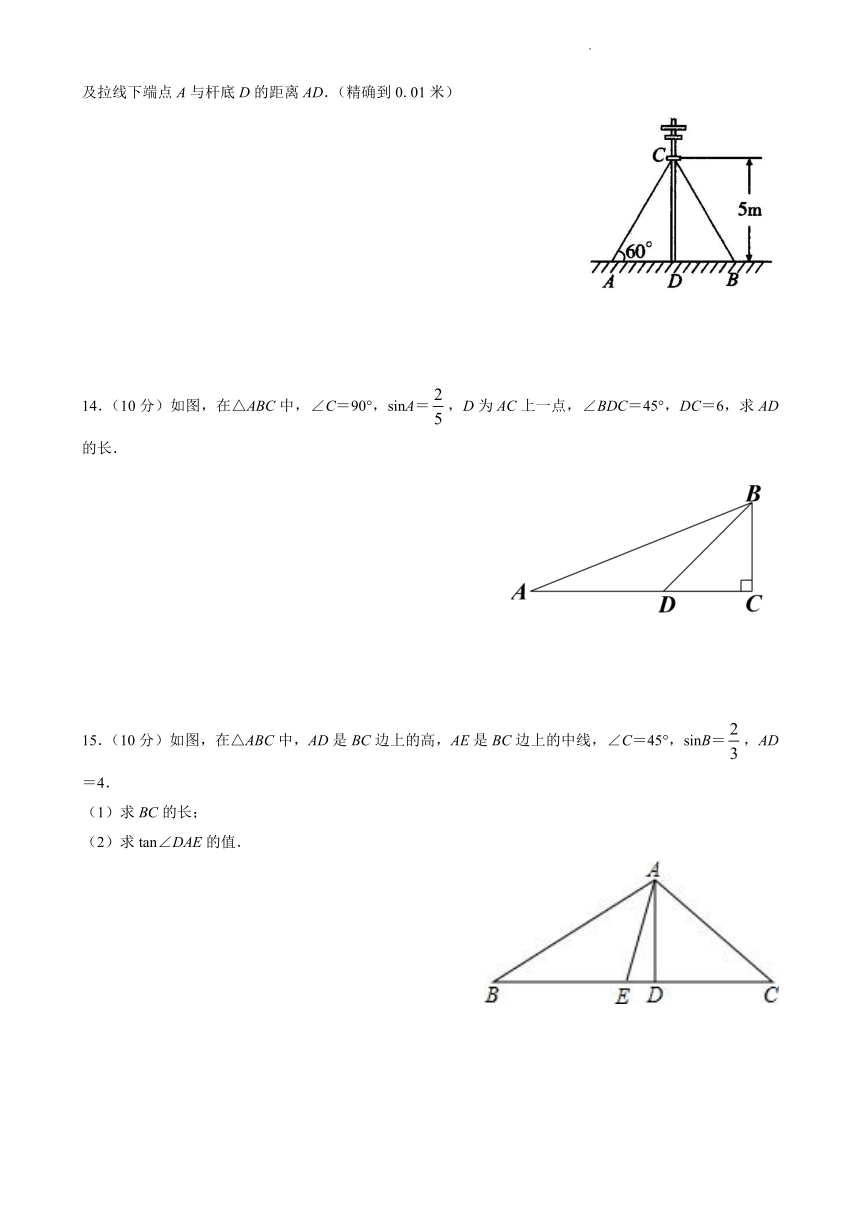
13.(10分)如图,在离地面高度5米的C处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD.(精确到0.01米)
14.(10分)如图,在△ABC中,∠C=90°,sinA=,D为AC上一点,∠BDC=45°,DC=6,求AD的长.
15.(10分)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=4.
(1)求BC的长;
(2)求tan∠DAE的值.
《解直角三角形》习题答案
1.C.
【解析】∵∠C=90°,∴,又∵AB=12,∴.故选C.
2.C.
【解析】在直角三角形中,根据角的余弦值与三角形边的关系,可求出BC边的长.
在Rt△ABC中,cosB=,∴BC=AB cos B=7cos 35°.故选C.
3.A.
【解析】过A作AE⊥CB于E.∵AB=3 cm,∠B=60°,∴sin 60°=,∴AE=,∴SABCD=BC AE=6.
故选A.
4.B.
【解析】过点B作BE⊥AD于E.设BE=x.∵∠BCD=60°,tan∠BCE=,∴CE=x.
在直角△ABE中,AE=x,AC=50米,则x-x=50.解得x=25.即小岛B到公路l的距离为25米.故选B.
5.D .
【解析】根据题意画出图形,分别利用解直角三角形的知识求出风筝的高再进行比较即可.如图,
甲中,AC=100m,∠C=30°,AB=100×sin30°=50m;
乙中,DF=100m,∠D=45°,DE=100×sin45°=50≈70.71m;
丙中,GI=95m,∠I=45°,GH=95×sin45°=≈67.18m;
丁中,JL=95m,∠L=60°,JK=95×sin60°=≈82.27m.
故选D.
6.8.
【解析】在直角△ABC中,利用正弦函数即可求解.试题解析:在Rt△ABC中,sin∠ABC=,
∴(米).
7..
【解析】在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
解:∵BC=6,sinA=,∴AB=10,∴AC=,∵D是AB的中点,∴AD=AB=5,
∵△ADE∽△ACB,∴ ,即,解得:DE=.
8.14a2.
【解析】过A作AD⊥BC于D.在Rt△ACD中,AC=5a,cos C=,
∴CD=AC cos C=3a,AD==4a.
在Rt△ABD中,AD=4a,∠B=45°,∴BD=AD=4a.∴BC=BD+CD=4a+3a=7a.
故S△ABC=BC AD=×7a×4a=14a2.故答案是14a2.
9.2.
【解析】如图,过点B作BE⊥AC,垂足为点E,AB的垂直平分线交AB于点F.
∵在△ABC中,AB=BC,∠B=120°,AC=6cm,
∴∠A=30°,AE=3cm. ∴AB=.
又∵DF是AB的垂直平分线,∴AF=. ∴AD=.
10.4
【解析】∵△BDE由△BCE翻折而成,∴BC=BD,∠BDE=∠C=90°.
∵AD=BD,∴AB=2BC,AE=BE.∴∠A=30°.
在Rt△ABC中,∵AC=6,∴BC=AC tan30°=6×=2.
设BE=x,则CE=6﹣x,
在Rt△BCE中,∵BC=2,BE=x,CE=6﹣x,
∴BE2=CE2+BC2,即x2=(6﹣x)2+(2)2,解得x=4.
∴折痕BE的长为4.
11.30°,,12.
【解析】根据三角形的内角和为180°,已知∠C,∠B,BC的值,则∠A=180°-∠B-∠C,从而求出c,b代入数值进行求解即可.
解:在Rt△ABC中,∠A=180°-90°-60°=30°,
∵cosB=,
∴c= ,
b=BCtan60°=.
12.AB =3+.
【解析】过点C作CD⊥AB于D.通过解三角形计算即可.
解:过点C作CD⊥AB于D.
在Rt△ACD中,∵∠A=30°,AC=
∴CD=,
∴AD=AC×cosA=×=3
在Rt△BCD中,∠B=45°,则BD=CD=,
∴AB=AD+BD=3+
13..
【解析】因为电线杆和拉线构成直角三角形,可利用三角函数的相关知识解答.
解:在Rt△ADC中,∵
∴(米)
∵
∴(米)
14..
【解析】由已知得△BDC为等腰直角三角形,所以CD=BC=6,又因为已知∠A的正弦值,即可求出AB的长,然后根据勾股定理求出AC的长,即可求出AD的长.
解:
在△BDC中,∠C=90°,∠BDC=45°,DC=6
∴tan45°==1
∴BC=6
在△ABC中,sinA=,∴,
∴AB=15
∴
15.(1);(2).
【解析】(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=4;解Rt△ADB,得出AB=6,根据勾股定理求出BD=2,然后根据BC=BD+DC即可求解;
(2)先由三角形的中线的定义求出CE的值,则DE=CE-CD,然后在Rt△ADE中根据正切函数的定义即可求解.
解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=4,
∴DC=AD=4.
在△ADB中,∵∠ADB=90°,sinB=,AD=4,
∴AB=
∴BD=,
∴BC=BD+DC=
(2)∵AE是BC边上的中线,
∴CE=BC=,
∴DE=CE-CD=,
∴tan∠DAE=.
一、选择题(每小题5分,共25分)
1.在Rt△ABC中,∠C=90°,AB=12,cos A=,则AC等于( )
A.36 B. C.4 D.
2.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为( )
A.7sin 35° B. C.7cos35° D.7tan35°
3.在平行四边形ABCD中,已知AB=3cm,BC=4cm,∠B=60°,则S□ABCD等于( )
A.cm2 B.cm2 C.cm2 D.cm2
4.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )
A.25 B. C. D.
(
同学
甲
乙
丙
丁
放出风筝线长(
m)
100
100
95
95
线与地面夹角
30
°
45
°
45
°
60
°
)
第4题图 第5题表
5.身高相等的四名同学甲乙丙丁一起参加风筝比较,四人放出风筝的线长、线与地面的夹角如上表所示(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题5分,共25分)
6.如图,离地面高度为5米的A处引拉线固定电线杆,要使拉线与地面a=37°,工作人员需买拉线的长度约为_____________(精确到米).(sin37°≈0.6,cos37°≈0.8)
第6题图 第7题图 第8题图
7.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE= .
8.如图,△ABC中,∠B=45°, cos∠C=,AC=5a,则△ABC的面积用含的式子表示是_______.
9.如图,在△ABC中,AB=BC,∠B=120°,AB的垂直平分线交AC于点D.若AC=6cm,则AD=________cm.
第9题图 第10题图
10.如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为 .
三、解答题(共50分)
11.(10分)如图,△ABC中,∠C=90°,∠B=60°,BC=6,求∠A及b、c.
12.(10分)如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长.
13.(10分)如图,在离地面高度5米的C处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD.(精确到0.01米)
14.(10分)如图,在△ABC中,∠C=90°,sinA=,D为AC上一点,∠BDC=45°,DC=6,求AD的长.
15.(10分)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=4.
(1)求BC的长;
(2)求tan∠DAE的值.
《解直角三角形》习题答案
1.C.
【解析】∵∠C=90°,∴,又∵AB=12,∴.故选C.
2.C.
【解析】在直角三角形中,根据角的余弦值与三角形边的关系,可求出BC边的长.
在Rt△ABC中,cosB=,∴BC=AB cos B=7cos 35°.故选C.
3.A.
【解析】过A作AE⊥CB于E.∵AB=3 cm,∠B=60°,∴sin 60°=,∴AE=,∴SABCD=BC AE=6.
故选A.
4.B.
【解析】过点B作BE⊥AD于E.设BE=x.∵∠BCD=60°,tan∠BCE=,∴CE=x.
在直角△ABE中,AE=x,AC=50米,则x-x=50.解得x=25.即小岛B到公路l的距离为25米.故选B.
5.D .
【解析】根据题意画出图形,分别利用解直角三角形的知识求出风筝的高再进行比较即可.如图,
甲中,AC=100m,∠C=30°,AB=100×sin30°=50m;
乙中,DF=100m,∠D=45°,DE=100×sin45°=50≈70.71m;
丙中,GI=95m,∠I=45°,GH=95×sin45°=≈67.18m;
丁中,JL=95m,∠L=60°,JK=95×sin60°=≈82.27m.
故选D.
6.8.
【解析】在直角△ABC中,利用正弦函数即可求解.试题解析:在Rt△ABC中,sin∠ABC=,
∴(米).
7..
【解析】在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
解:∵BC=6,sinA=,∴AB=10,∴AC=,∵D是AB的中点,∴AD=AB=5,
∵△ADE∽△ACB,∴ ,即,解得:DE=.
8.14a2.
【解析】过A作AD⊥BC于D.在Rt△ACD中,AC=5a,cos C=,
∴CD=AC cos C=3a,AD==4a.
在Rt△ABD中,AD=4a,∠B=45°,∴BD=AD=4a.∴BC=BD+CD=4a+3a=7a.
故S△ABC=BC AD=×7a×4a=14a2.故答案是14a2.
9.2.
【解析】如图,过点B作BE⊥AC,垂足为点E,AB的垂直平分线交AB于点F.
∵在△ABC中,AB=BC,∠B=120°,AC=6cm,
∴∠A=30°,AE=3cm. ∴AB=.
又∵DF是AB的垂直平分线,∴AF=. ∴AD=.
10.4
【解析】∵△BDE由△BCE翻折而成,∴BC=BD,∠BDE=∠C=90°.
∵AD=BD,∴AB=2BC,AE=BE.∴∠A=30°.
在Rt△ABC中,∵AC=6,∴BC=AC tan30°=6×=2.
设BE=x,则CE=6﹣x,
在Rt△BCE中,∵BC=2,BE=x,CE=6﹣x,
∴BE2=CE2+BC2,即x2=(6﹣x)2+(2)2,解得x=4.
∴折痕BE的长为4.
11.30°,,12.
【解析】根据三角形的内角和为180°,已知∠C,∠B,BC的值,则∠A=180°-∠B-∠C,从而求出c,b代入数值进行求解即可.
解:在Rt△ABC中,∠A=180°-90°-60°=30°,
∵cosB=,
∴c= ,
b=BCtan60°=.
12.AB =3+.
【解析】过点C作CD⊥AB于D.通过解三角形计算即可.
解:过点C作CD⊥AB于D.
在Rt△ACD中,∵∠A=30°,AC=
∴CD=,
∴AD=AC×cosA=×=3
在Rt△BCD中,∠B=45°,则BD=CD=,
∴AB=AD+BD=3+
13..
【解析】因为电线杆和拉线构成直角三角形,可利用三角函数的相关知识解答.
解:在Rt△ADC中,∵
∴(米)
∵
∴(米)
14..
【解析】由已知得△BDC为等腰直角三角形,所以CD=BC=6,又因为已知∠A的正弦值,即可求出AB的长,然后根据勾股定理求出AC的长,即可求出AD的长.
解:
在△BDC中,∠C=90°,∠BDC=45°,DC=6
∴tan45°==1
∴BC=6
在△ABC中,sinA=,∴,
∴AB=15
∴
15.(1);(2).
【解析】(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=4;解Rt△ADB,得出AB=6,根据勾股定理求出BD=2,然后根据BC=BD+DC即可求解;
(2)先由三角形的中线的定义求出CE的值,则DE=CE-CD,然后在Rt△ADE中根据正切函数的定义即可求解.
解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=4,
∴DC=AD=4.
在△ADB中,∵∠ADB=90°,sinB=,AD=4,
∴AB=
∴BD=,
∴BC=BD+DC=
(2)∵AE是BC边上的中线,
∴CE=BC=,
∴DE=CE-CD=,
∴tan∠DAE=.
